基于改进分水岭-凹点分割的矿石粒径分级检测方法
曾凡智,黄子豪,周 燕,谭振伟,余家豪
(佛山科学技术学院 电子信息工程学院,广东 佛山 528000)
0 引言
近年来,随着土木建筑行业的快速发展,国内外各类建筑行业对矿石骨料的需求量不断上升。矿产资源随着过度采集日渐减少,某些地区甚至出现矿石骨料资源生产紧缺等现象。因此,提高骨料配比的利用率,充分提高建材质量成为各个混凝土企业近年来研究的重点。目前,提高矿石骨料利用率的方法还在不断研究,其中较为普遍的方法是建立矿石粒径分级模型,从而提高骨料混合配比的质量,实现骨料不同粒径的有效利用。
传统的人工筛分主要利用筛分桶过滤不同粒径的矿石,根据不同孔径规格的石子筛对其进行分级。首先将不同孔径规格的石子筛(单位:mm)由大到小层级堆叠成筛分桶。通过设置筛分时间后,启动振筛机对筛分桶剧烈晃动,使不同粒径的矿石掉落在各个规格的石子筛中。最后将每个级配筛分得到的矿石颗粒倒入电子秤称重,统计不同粒径占比的分级结果。传统的人工筛分需要工人协调和统计整个筛分过程,从而造成大量时间的耗费。而且,由于振筛机的剧烈晃动会对检测结果产生一定的影响,造成检测误差。因此,寻找一种高效准确的矿石粒径分级检测方法已迫在眉睫,成为该领域研究的重点。
国外早在21世纪初率先提出将计算机视觉技术引入到矿石粒径的检测中。S.AI-Thyabat等人通过测量矿石等效面积和平均直径两个参数,推测出每个矿石的外轮廓,然后将检测出来的外轮廓应用在多种不同形状大小的矿石颗粒,虽然该方法实验效果较好,但无法解决复杂环境下矿石堆叠的问题。H.Shang等人提出了基于神经网络模型,该模型通过筛分测量仪器得到分级的数据来模拟工业生产过程中矿石粒径的实时检测[5]。该方法虽然能比较准确检测出矿石粒径的分布,但在不同种类的矿石检测中存在数据波动较大的情况。近年来,为了解决矿石之间存在堆叠和粘连造成遮挡的问题,许多研究者将研究的重点转向矿石图像分割。罗小燕等人[6]在提取矿石图像特征的基础上,通过建立不同大小的检测算子,对分水岭算法分割后的图像采用击中与击不中的数据统计法,得到矿石的粒径分布。该方法识别精度不高,缺乏准确性。为了解决矿石图像中粘连导致无法有效分割的问题,张建立等人[7]提出多尺度形态学下的改进分水岭变换分割方法。该方法虽然能够较为真实反映矿石粒径的分布,但识别效率低,缺乏实时性。为了提高矿石图像分割算法的有效性,孙国栋等人采用超像素与领域超像素之间的线性表达来建立一种边缘领域亲和度图,通过该方法能准确分割不同光照强度和噪声下的矿石颗粒边界,但无法对矿石粒径进行有效分级[8]。
总结上述方法存在不足的问题,本文提出一种基于改进分水岭-凹点分割的矿石粒径分级检测方法,首先对矿石图像进行增强,提取出矿石之间的边缘轮廓。根据矿石识别边缘轮廓的像素面积,利用反向链码寻找对称角置信辐射区域,判断矿石之间的粘连位置是否存在明显的凹点,通过匹配凹点的最短距离进行融合分割[9]。将同一个粒径级配的矿石进行归类,从而达到实时检测的目的,降低检测的误差率,从而提高算法的泛化能力和鲁棒性。
1 图像处理流程
本文主要研究生产线车间抽样采集的矿石图像,由于皮带上待检测的矿石处于粘连堆叠状态,因此需要将矿石在图像背景上进行区分。首先将采集的矿石图像进行预处理操作,从而得到形态学优化后的二值化图像。通过改进的分水岭算法,解决矿石边缘信息丢失导致过分割的问题。引入凹点分割算法[10],优化矿石之间粘连产生欠分割的情况。最后统计不同粒径区间的像素面积,得出粒径分级占比的结果。图像处理流程如图1所示。
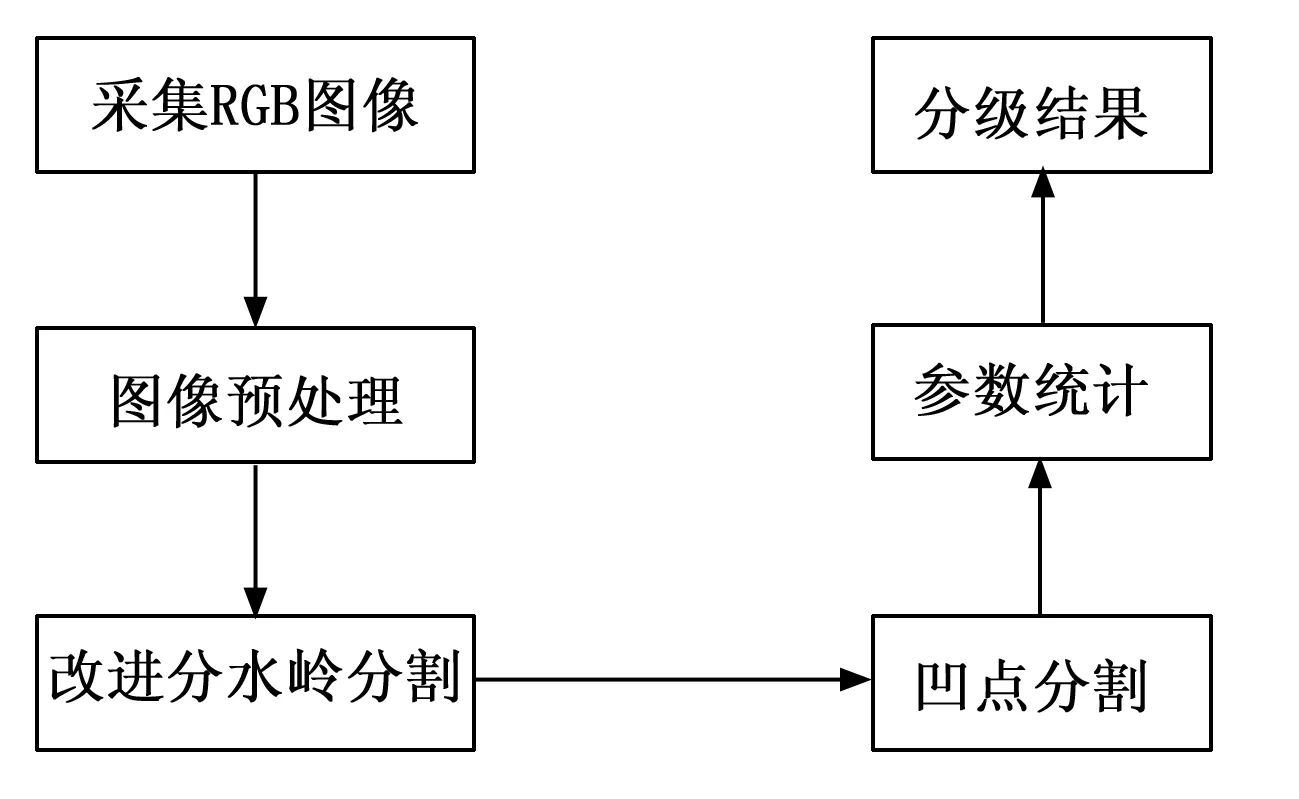
图1 图像处理流程图
2 图像预处理
2.1 图像增强
由于采集的矿石存在形状和纹理的不同,造成图像灰度和色彩亮度上的差异,使堆叠的矿石难以从图像背景中区分。为了能更加清晰展示矿石之间的特征,需要对原始采集的图像进行亮度和灰度变换。如图2所示,图像经过亮度变换和灰度化后,图像质量明显得到提升,矿石边缘和轮廓更加清晰,同时减少背景的干扰,降低图像的数据量计算。但由于灰度化处理后的图像仍存在噪点,因此需要对图像进行滤波去噪处理。

图2 图像增强流程图
2.2 自适应中值滤波
图像经过增强后效果得到一定的提升,但由于现场生产环境比较恶劣,空气中弥漫着大量的粉尘,生产线设备发出的噪声也会对图像造成影响。为了去除图像中的噪点信息,需要对图像进行滤波处理。图像滤波主要包括均值滤波、中值滤波、高斯滤波、双边滤波等。结合现场的生产环境分析,相比于其他滤波,中值滤波去除噪点的能力比较强,特别是处理存在噪声干扰的环境下拍摄的图像。经过中值滤波处理后,不会出现图像失真的情况,能比较完整保留图像的细节。中值滤波表达式如式(1)所示:
g(x,y)=median{f(x,y)},(x,y)∈S
(1)
式中,f(x,y)为原图像像素的灰度值,g(x,y)为滤波结果输出的图像。
然而,使用中值滤波并不能完全检测图像全局的像素信息。当图像边缘模糊时,边界纹理则相对粗糙。从矿石形态、纹理多样的角度上考虑,算法处理矿石图像时需要较高的自适应度。因此,采用自适应中值滤波[11],在去噪的同时,又能很好地保留矿石边缘的特征。使用自适应中值滤波,通过设置最小滤波值和最大滤波值,自适应判断噪声敏感度,从而对矿石边缘与背景之间的像素形成有效地渐变。自适应中值滤波如式(2)所示:
g′(x,y)=median{f(x,y),kmin,kmax,(x,y)∈S}
(2)
本文设置最小滤波值kmin为3,最大滤波值kmax为7。如图3(c)所示,与中值滤波相比,自适应中值滤波不仅能有效去除图像的噪声,同时能保留图像更多的细节,提升矿石边界特征与背景之间的对比度,提升矿石边缘的局部形态特征。

图3 滤波效果对比图
2.3 形态学重构
图像经过滤波处理后,还存在局部粘连堆叠的情况。为了避免图像分割时产生欠分割和过分割的现象,使用多尺度形态学重构的方法对图像中心区域进行优化。多尺度形态学[12]利用形态学的开闭运算对梯度图像进行重构,保留重要区域的同时去除细节和噪声,避免了图像局部极值过多而产生非规则的灰度渐变和噪点干扰,使分割后的图像在区域边缘具有较准确的定位能力。其中,腐蚀和膨胀[13]是形态学中最基本的操作。假设图像A(x,y)表示二值化图像,B(i,j)表示结构元素,R(u,v)表示掩码图像,则形态学腐蚀和膨胀操作分别如式(3)、式(4)所示:
AΘB=
min{A(x+i,y+j)-B(i,j)|(x,y)∈Df,(i,j)∈Db}
(3)
A⊕B=
max{A(x-i,y-j)+B(i,j)|(x,y)∈Df,(i,j)∈Db}
(4)
式中,Θ为腐蚀运算,⊕为膨胀运算,Df为图像A(x,y)的定义域,Db为结构元素B(i,j)的定义域。
本文针对形态学方法进行改进,如图4所示,改进的形态学重构算法流程如下:

图4 形态学重构流程图
1)针对矿石图像的特征采用不同的矩阵结构过滤。首先对滤波图像进行二值化,然后对其进行开操作,消除图像中背景干扰的细小区域,平滑矿石颗粒间隙的位置,去除图像中的噪点和孔洞。开操作表达式如式(5)所示:
C(x,y)=(AΘB)⊕B
(5)
2)图像经过开操作后,部分纹理和边界区域得到了优化。将开操作后的图像进行腐蚀操作,对腐蚀后的图像取补后利用蒙版进行二值化重构。二值化重构操作表达式如式(6)所示:
D(x,y)=u(CΘB)∪R(u,v)
(6)
3)为了扩大矿石颗粒边缘的灰度值,减少矿石颗粒之间产生粘连,将重构后的二值化图像进行膨胀操作。经过膨胀操作后,矿石的亮度得到增强,使轮廓信息更加清晰。膨胀操作表达式如式(7)所示:
E(x,y)=D⊕B
(7)
4)最后将膨胀后的图像进行高斯线性平滑处理。如图4(d)所示,利用高斯线性平滑,使图像中的目标轮廓边缘得到填充,同时将图像中的孔洞进行填充,从而比较完整的保留矿石边缘特征。线性平滑操作表达式如式(8)~(9)所示:
(8)
G′(x,y)=G(x,y,σ)*E
(9)
3 基于改进分水岭-凹点融合分割
3.1 改进的分水岭分割算法
传统的分水岭分割[14-16]算法直接用于提取区域中心梯度图像,图像分割效果在一定程度上取决于图像的质量。矿石图像经过形态学优化后虽然效果得到了提升,但无法避免图像中仍然存在噪点的影响。直接使用分水岭分割会导致矿石粘连欠分割的情况,无法准确识别边缘信息,从而对检测的精度造成影响。本文针对上述的问题对传统的分水岭分割算法进行改进。
1)对形态学重构后的矿石图像进行前景区域的距离变换。通过图像二值化后生成的矿石区域,计算所有像素点到其最近背景区域零像素点的距离,将距离等价为前景与背景的灰度差值,形成新的灰度图像。
2)统计灰度图像的连通区域,根据矿石颗粒的大小,寻找连通区域的局部极大值。对图像中的缝隙背景、矿石目标根据像素值的不同进行标记。当图像扫描完后,根据标记值的不同,提取图像中的局部最大值作为标记符,得到矿石目标在图像上的所有连通区域。
3)将形态学重构的图像与距离变换后的二值化图像做差值运算,遍历图像的差值像素,统计非零像素。并在连通区域标记图上对应的位置打上标记作为分水岭掩膜标记。掩模标记处于矿石之间的边缘位置,通过标记能突出矿石粘连的部分。
4)根据分水岭掩模标记可得到矿石颗粒边缘的分水岭脊线,利用连通区域的标记符沿脊线梯度最小化来修正梯度图像,使其在矿石缝隙的位置存在局部最小值,将修正后的梯度图像进行分水岭分割。
3.2 凹点分割
对距离变换后的矿石图像采用改进的分水岭算法,利用标记的连通区域生长,使图像边缘轮廓保留完整的区域,在一定程度上消除了过分割的现象。但由于原始的矿石图像颜色不均匀,纹理比较复杂,矿石之间容易产生堆叠。为了消除图像粘连导致欠分割的现象,本文采用凹点分割方法,通过连通区域提取矿石轮廓的面积进行粘连判断,将凸缺陷面积由大到小排序后筛选出候选凹点,最后利用凹点最短邻近法实现粘连区域的分割,具体步骤的实现如下。
3.2.1 粘连区域的判定
由于矿石颗粒的纹理和形状存在多样化,矿石平铺在皮带上容易产生堆叠,导致矿石之间的边缘形成粘连。因此,需要通过计算矿石连通区域轮廓的形状因子[17]作为判别矿石粘连的依据。形状因子Sf的表达式如式(10)所示:
(10)
式中,A表示矿石连通区域的面积,L表示连通区域的周长,l表示矿石外接矩形的长边,d表示矿石外接矩阵的短边,Sf形状因子的取值范围为[0,1]。当矿石在无粘连的情况下,连通区域趋于圆形时,形状因子越接近于1。相反,若矿石粘连越严重,形状因子则越趋于0。
如图5所示,3个连通区域的形状因子分别为0.13、0.37、0.76。根据分析,形状因子能区分矿石之间是否产生粘连,并且能反映出粘连的严重程度。本文将形状因子的阈值SF设置为0.45,当某个连通区域满足Sf 图5 形状因子图 3.2.2 凹点检测 由于矿石颗粒的大小和形状不规则,若多个矿石之间产生堆叠,粘连区域的轮廓则会形成凹点。首先提取粘连区域,沿着轮廓的边缘将缺陷的部分进行填补,粘连区域形成的凸多边形即为凹包。将凹包与粘连区域做差值运算,所得到的结果即为凸缺陷。其次,统计凸缺陷的个数,将计算得到凸缺陷的面积按照递减的方式进行排序。为了避免出现多余的凹点,将面积小于50像素的凹包进行排除过滤。最后将待处理的凸缺陷按面积从大到小以集合的形式储存,将凸缺陷进行匹配操作。 3.2.3 凹点匹配 凸缺陷是由矿石粘连处的凹区域所形成的。针对矿石之间存在复杂粘连而产生不规则凹区域的情况,本文提出一种基于反向链码对角凹点矢量匹配法[18]。反向链码的表达式如式(11)所示: (11) 原始的反向链码不具有旋转不变性。因此,本文对反向链码进行差分和归一化处理,使其具有几何旋转不变性。差分归一化处理的过程如式(12)所示: (12) 式中,mod表示模运算,N表示链码方向数,S′表示形状旋转后轮廓像素的坐标点,M′表示形状旋转后的新链码。 由于物体之间形成的粘连具有一定的相似对称性。通过凸缺陷形成的夹角在反向链码中匹配对应的角度,从而寻找另一凹点在该夹角的对称置信辐射区域内,以最短距离作为划线分割。具体的步骤如下: 1)提取凸缺陷的边缘轮廓,获取目标轮廓的所有角点,根据像素坐标的规则确定3个边缘角点。由于凹点位于轮廓双边局部曲率最大,通过计算目标轮廓的区域,确定凸缺陷凹点的位置,将其余两个角点用直线连接构成矢量夹角。 2)将所有凸缺陷根据夹角的形状和角度在反向链码表中标记出相对应的位置。延长夹角的对角线,扩大置信辐射区的范围。如图6所示,以当前点、前继点与后继点形成凹点夹角∠man,存在另一凹点b在该夹角的对称角置信辐射区域内。 图6 反向链码对应的置信辐射区域图 3)当所有凸缺陷在反向链码中标记后,若反向链码中不存在相似重合的夹角,则称为串联粘连。如图7(a)所示,对于串联粘连,若延长线的对称角包含于单个对称凹区域内,且对称角的置信辐射区落在某个凹区域的矢量夹角内,则表明该区域存在粘连目标,直接将两个凹点进行划线连接。 图7 基于反向链码凹点匹配图 4)如果反向链码中存在两个或多个相似重合的夹角,则称作并联粘连。如图7(b)所示,对于并联粘连,由于反向链码中存在两个或多个以上的凹区域形成矢量夹角,无法直接判断粘连是由哪两个凹区域形成,则需要根据凸缺陷上的凹点位置用欧式距离计算凹点之间的最短距离。 本文将改进的分水岭算法与凹点分割算法进行融合,既能减少图像过分割的情况,又能优化矿石颗粒粘连导致凹点分割不完整的问题。通过将两种分割算法相结合,从而解决单个算法中存在的分割问题。 当图像完成算法分割后,此时通过提取每块矿石颗粒的轮廓,计算等效粒径后对其进行粒径分级。矿石粒径分级是检测过程中最重要的步骤,同时也是对混凝土骨料配比和矿石采样检测的质量评判的重要依据。如图8所示,通过提取矿石颗粒的表征参数,计算采样矿石群的特征参数。其中表征参数包括面积、周长、长轴和短轴,特征参数主要将矿石等效粒径和粒径分级作为评估指标。具体的定义分别如下: 图8 矿石颗粒参数图 等效粒径是评判矿石形状和外观的指标。利用最小外接矩形沿着矿石的轮廓区域进行拟合,提取的最小外接矩形的长边为长轴,短边为短轴。其中,等效粒径d的计算方式如式(13)所示: (13) 式中,A表示矿石投影面积所占的像素,L表示矿石轮廓周长的像素。 粒径分级表示不同粒径范围内矿石颗粒像素面积的占比,粒径分级区间能直观反映出某个批次样品采样的均衡性。按照国家骨料的检验标准选取代表粒径规格s1,s2,...,st组成粒径区间[s1,s2],...,[st-1,st],则矿石粒径分级占比率si的表达式如式(14)所示: (14) 式中,St为矿石颗粒在粒径区间[st-1,st]内累积的像素面积,T为矿石群的总像素面积。 本文在骨料实验室的现场搭建矿石粒径分级检测系统以及图像采集装置。图像采集装置主要由CCD工业摄像头(2 K分辨率,即2 048 px*1 080 px)、支架、继电器、光源、计算机以及矿石皮带组成。摄像头固定安装在支架上,与计算机直接相连,光源用于提高图像采集质量和亮度。矿石粒径分级检测系统主要包括图像采集模块、算法处理模块和数据展示模块。图像采集模块利用海康图像采集工具包调用CCD摄像头实现视频流实时预览,可连续采集矿石图像。算法处理模块采用本文算法对采集的矿石图像进行粒径检测,数据展示模块将检测得到的粒径分级数据展示在界面上。系统架构如图9所示。 图9 系统架构图 本系统开发主要采用Pyqt5界面和Python编程语言,系统实现矿石粒径检测功能的具体流程如下: 1)在系统界面上,点击“打开相机”按钮,启动摄像头,通过调整合适的参数,将摄像头捕获的矿石图像显示在界面上。 2)点击“图像采集”按钮,通过视频流实时采集待检测的矿石图像。 3)点击“开始检测”按钮,系统将检测的图像传送至后端,通过调用本文实现的改进分水岭-凹点分割算法,得到各个粒径分级检测的结果。 4)如图10所示,系统将矿石图像分级检测的结果以及其他参数以柱状图和饼图的形式在界面上展示。 图10 系统检测界面图 矿石各粒径级配的占比是骨料混合配比的重要评判指标[19-20],为了验证本文提出的算法分割效果以及准确率,本文采集5 kg矿石按照四分法均匀抽样3 kg作为1组试验检测。首先按照国家制定的《普通混凝土用砂、石质量及检测方法标准》设置粒径分级区间,根据规则将矿石粒径划分为0~2.36,2.36~4.75,4.75~9.5,9.5~16.0,16.0~19.0,19.0~26.5,26.5~31.5,31.5~37.5,37.5~53.0共9个粒径区间(单位:mm)。为了得到矿石粒径区间在图像上的像素信息,在检测之前建立粒径区间的像素尺寸与实际测量尺寸的对应关系。在摄像头的投影下,根据拍摄的参照物尺寸长度统计图像像素点的个数,将其换算成比例系数。标定的比例系数f换算过程如式(15)所示: (15) 式中,V表示标定图像的像素(px),R表示标定参照物的实际尺寸(mm)。 通过比例系数f,从而得到每个粒径区间的投影像素尺寸Pi。Pi的计算如式(16)所示: Pi=xi*f (16) 式中,xi表示第i个粒径区间的实际尺寸,Pi表示第i个粒径区间的像素。 人工筛分与算法检测的累积率gn、pn的表达式分别如式(17)、(18)所示: (17) (18) 式中,在实际人工筛分的过程中,Gi表示第i个粒径区间矿石累积的质量,G表示抽样筛分矿石的总质量。在算法检测的过程中,Psi表示第i个粒径区间矿石累积的像素面积,P表示算法分割矿石的总像素面积。 累积误差率主要反映人工筛分与算法检测中每个粒径分级之间累积的相对误差,累积误差率Er的计算方式如式(19)所示: Er=|gn-pn| (19) 为了验证算法对矿石粒径检测的准确性,将采样的矿石随机平铺放置在皮带上进行3组粒径检测试验。人工筛分与算法检测结果对比如表1所示。 表1 矿石粒径检测统计表 % 从表1中的数据分析,对于第一组检测,粒径4.75~9.5的误差最大,累积误差率为3.07%;对于第二组检测,粒径4.75~9.5的误差最大,累积误差率为4.47%;对于第三组检测,粒径2.36~4.75的误差最大,累积误差率为2.35%。从各级的数据分布中发现,三组样品的误差率存在一个大致的变化规律。偏小粒径的矿石由于堆叠容易产生遮挡的现象,从而导致偏小粒径的矿石存在误检。随着粒径尺寸逐渐增大,误差率整体呈现下降的趋势,粒径较大的矿石由于边缘轮廓比较清晰,分割比较完整,使得误差率局部最小。实验结果表明,各组最大累积误差率在5%以内,可以满足实际生产的需求。 为了验证算法对不同粒径的矿石数量分割的准确性,将人工筛分的结果与本文算法进行5组粒度计数对比试验,人工粒度计数与算法统计的结果对比如表2所示。对检测结果统计其累计误差率,其中累计误差率计算方法如式(20)所示: 表2 矿石颗粒个数分布统计表 (20) 式中,Pr为粒径r的累计误差率,Exi为人工筛分得到第i组粒径范围内的矿石个数,Ei为本文算法得到第i组粒径范围内的矿石个数,Ni为第i组检测总矿石的个数。 从表2中的数据分析,对于粒径2.36~4.75的矿石,其检测对比的累计误差率最大,约为4.55%。由于小颗粒的矿石粒径比较小,容易产生遮挡,导致漏检的情况,从而造成检测误差相对较大。而较大的矿石颗粒检测更为准确。随着矿石粒径的增大,累计误差率逐渐减少,检测结果越来越精确。从5组的试验中表明,各个粒径的累计误差率不超过5%。因此,本文算法对矿石粒径实时检测比较准确,能替代传统人工筛分的工业应用场景。 为了验证算法的分割效果,本文从算法分割的结果图以及准确率方面进行对比验证分析。通过对比OSTU阈值分割、传统分水岭分割与本文提出的改进分水岭-凹点分割,对矿石图像进行算法分割试验。算法分割的结果如图11所示。 图11 不同算法分割的结果图 图11(a)为待分割的矿石图像。图11(b)为OSTU阈值分割结果图,该算法只能分割出大致的矿石目标轮廓,没有形成闭合的连通区域。图像中还存在大量的噪点和孔洞,对于粒径较小的矿石分割效果很差,没有完全将矿石颗粒分割出来。图11(c)经过改进的形态学重构后,使用传统的分水岭算法,虽然图像中的矿石噪点和表面纹理得到消除和平滑,但由于矿石的堆叠,存在欠分割的情况。同时矿石之间局部粘连较为严重,造成一定的误差。图11(d)中使用改进的分水岭算法优化了个别矿石边缘分割不够完整的问题,同时增强了粒径较小的矿石纹理特征,通过结合凹点分割算法,解决了矿石堆叠造成欠分割的问题。因此,本文提出的改进分水岭-凹点分割算法能有效对粘连区域的矿石进行分割,将目标完整准确地从图像分割出来,从而得到良好的分割效果。 由图12中的数据分析,OSTU阈值分割的累积误差率最大。而本文算法相对于其他分割算法,累积误差率最小。本文算法与人工筛分相比,最大累积误差率为3.41%,最小累积误差率为0.30%,平均累积误差率为1.17%,均在实际生产的误差允许范围内。因此,本文提出的算法具有较高的可行性与准确性。 图12 不同算法分割的累积误差率图 本文对传统的矿石骨料分割算法进行改进,为了提高采集的矿石图像质量,首先对图像进行亮度变换和灰度化,便于区分检测的矿石目标和背景。利用自适应中值滤波,消除图像上的噪声并完整保留矿石边缘的特征信息。利用改进的形态学重构方法,平滑矿石图像中边缘区域的纹理,消除二值图像中矿石局部的噪点和孔洞。使用改进的分水岭分割方法,减少图像边缘过分割现象,同时引入凹点分割方法,解决了矿石堆叠所造成遮挡欠分割的问题。将两种方法相结合,有效解决了单个分割算法存在的弊端,通过实验验证,本文提出的方法具有可行性与鲁棒性。 本文提出改进分水岭-凹点分割算法的检测结果与人工筛分的结果进行对比,从数据分析得出,各个粒径之间的最大累积误差率在5%以内,从而验证了本文提出的方法具有较高的准确率,为人工智能化矿石粒径分级检测的研究提供依据。在今后的研究中,将推进应用于流水线的生产检测,提升国内混凝土企业的工业智能化生产和行业生态环境。
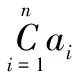


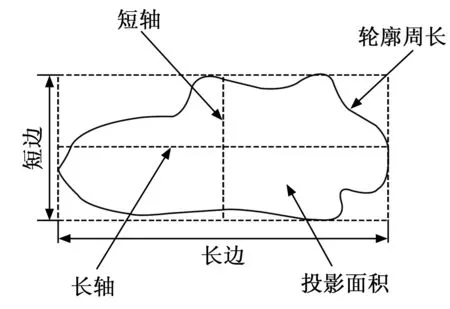
3.3 矿石特征参数提取
4 实验与结果分析
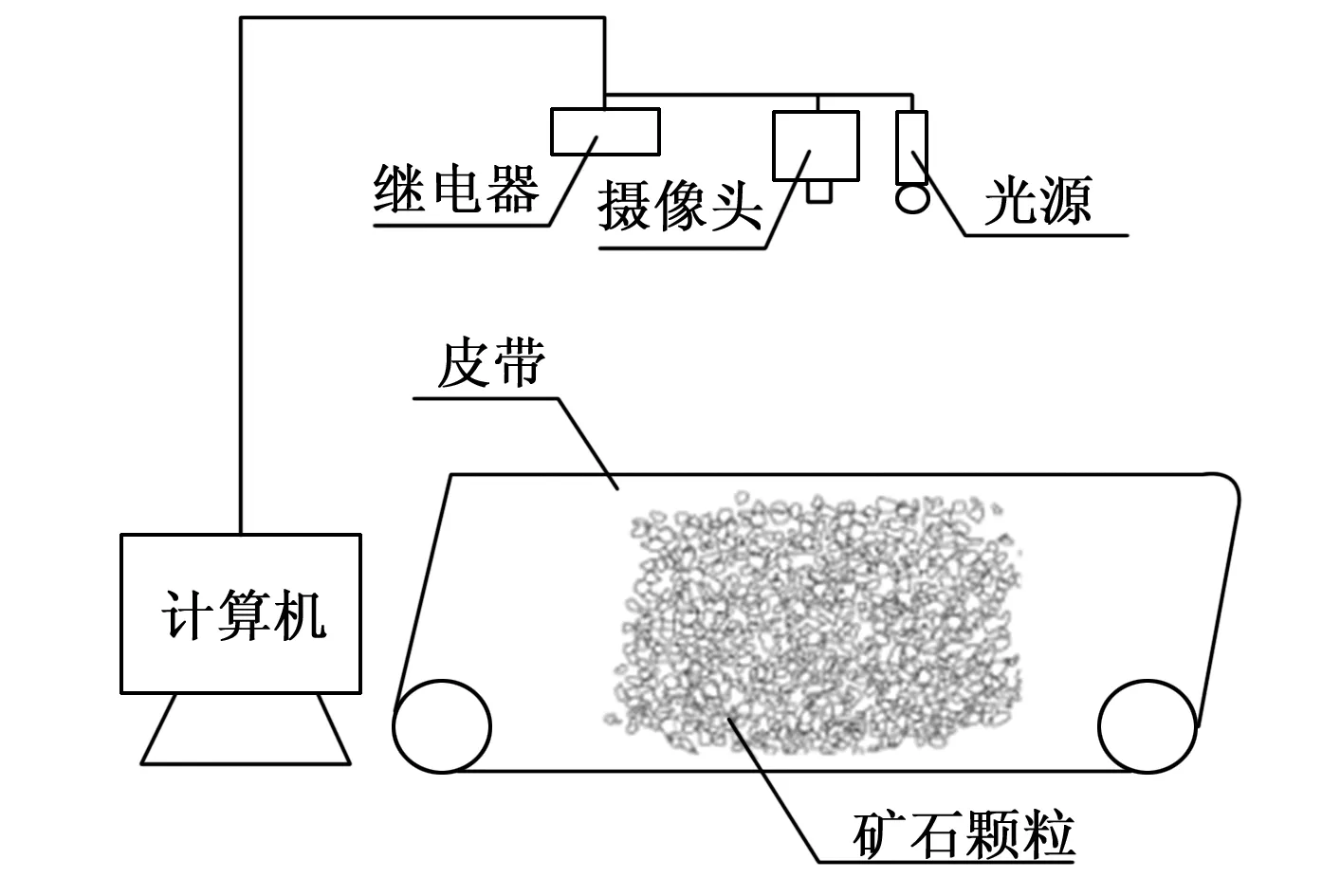
4.1 实验环境与系统实现

4.2 粒径检测试验

4.3 粒度计数试验

4.4 分割算法效果对比试验


5 结束语

