椭圆切线方程的多向推导及应用

高成龙

(天津外国语大学附属外国语学校,天津 300230)

椭圆的切线问题是高中数学中的重要知识,也是高考考查的重点内容,2022年天津卷第19题、2021年天津卷19题都考查了椭圆的切线.

1 椭圆切线方程的探究

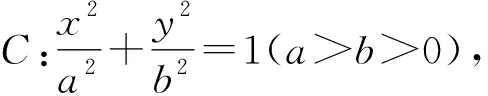
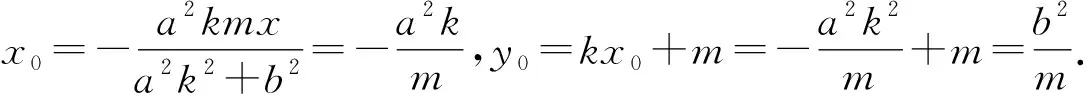
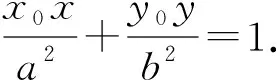
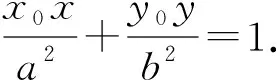
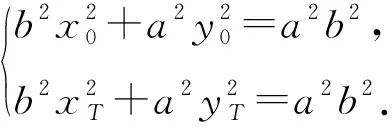
a2(yT+y0)(yT-y0)=-b2(xT+x0)(xT-x0).

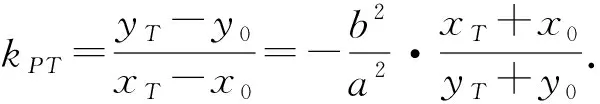
利用割线逼近切线的思想,当点T无限趋近于点P时,割线PT可近似看作椭圆在点P处的切线,此时割线PT的斜率即为椭圆在点P处的切线斜率,这一过程可以用极限思想表达为

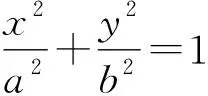
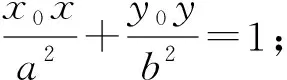
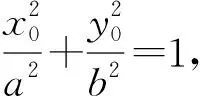
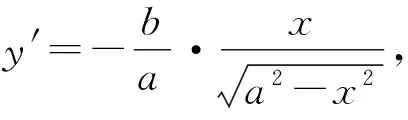
由直线的点斜式得切线方程为

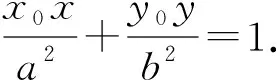
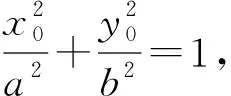
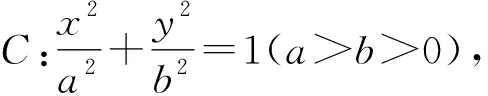
证明设l:y=kx+m,联立椭圆方程并消去y,得b2x2+a2y2=(a2k2+b2)x2+2a2kmx+a2m2-a2b2=0.

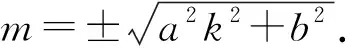
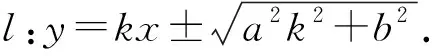
点评模型2说明了斜率一定的直线若与椭圆相切,则存在两条切线,它们分别位于坐标原点两侧.

2 椭圆切线方程模型的应用

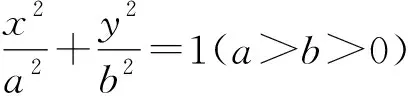
(1)求椭圆的方程;

(2)直线l与椭圆有唯一的公共点M,与y轴的正半轴交于点N,过点N与BF垂直的直线交x轴于点P,若MP∥BF,求直线l的方程.

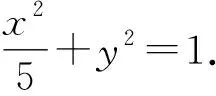
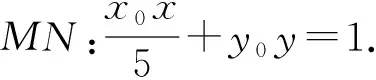
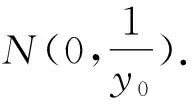
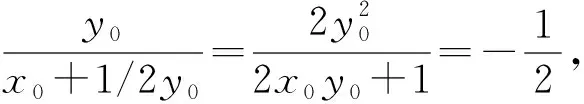
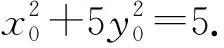
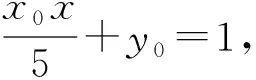
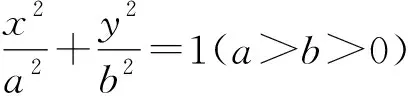
(1)求椭圆的离心率e;

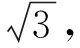
对于(2),由(1)得a2=3b2.

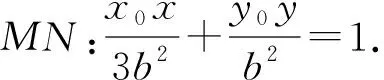
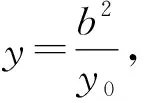
①

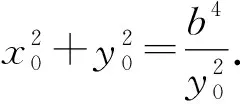
②

③

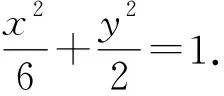
3 切线方程模型推广

模型4已知抛物线C:y2=2px(p>0),点P(x0,y0)为抛物线C上任意一点,则在点P处的切线方程为y0·y=p(x0+x).

运用类比思想将椭圆切线方程推广到双曲线、抛物线中去,进一步揭示了圆锥曲线切线的本质和规律,这一过程体现了知识迁移和类比思想在研究圆锥曲线中的重要性[1].