复杂网络能控性鲁棒性最优攻击序列研究
邓 浩,武瑞梓,于卓然,李均利
(四川师范大学 计算机科学学院,成都 610101)
1 引 言
复杂网络能控性(controllability)是复杂网络控制理论研究中的一个核心问题[1-4],指在有限时间内,通过适当且有限的控制输入,控制网络从任意初始状态到达任意给定目标状态的能力.复杂网络在攻击下维持能控性的能力称为能控性鲁棒性(controllability robustness)[5].能控性鲁棒性好的网络系统具有更好的抵御攻击的能力,同时也能为攻击后的补救争取时间,延迟系统的整体瘫痪.相反地,能控性鲁棒性差的系统则容易在受到攻击以后,迅速导致网络系统的整体失效.这个过程可以视为复杂网络在一个特定攻击序列下,网络能控性的变化情况,是一个动态的过程.不同攻击序列会引起能控性的不同变化情况.通常使用仿真来计算复杂网络的能控性鲁棒性[6,7],同时,深度学习也被应用于预测网络的能控性鲁棒性[8-11].
由于节点攻击比连边攻击更具破坏力[12],本文以节点攻击为研究对象,旨在寻找能够对复杂网络能控性带来最大破坏程度的攻击节点序列.网络在最优的攻击序列下表现出来的能控性鲁棒性可以视为其能控性鲁棒性的下限,为进一步测试、评估和优化复杂网络拓扑结构提供依据和线索.网络的最优攻击序列问题是一个NP-hard问题,很难通过理论方法求得最优解.
根据目标选择的不同,网络节点攻击可分为随机攻击和蓄意攻击.随机攻击是指以随机选择节点进行攻击.蓄意攻击通常假设攻击者具有对被攻击网络的必要知识,按一定特征选择最有效的节点进行攻击,如度数攻击[13]、介数攻击[14]、破坏性攻击[15]、邻里相似度攻击[16]、结构孔攻击[17]、层级攻击[18]等.通常蓄意攻击的破坏效果较随机攻击更明显.
根据不同的攻击意图,可以分为节点攻击序列和节点攻击集合的优化问题.节点攻击序列指节点攻击时,特定节点攻击顺序;而节点攻击集合则将一组节点作为一个整体攻击目标.前者更注重攻击的过程,而后者更注重攻击的结果.对于一个N节点网络,攻击节点序列的解空间大小为N!,攻击节点集合的解空间大小为2N.从解空间大小看来,攻击序列问题比攻击节点集合问题更为复杂.
根据不同的攻击序列生成方式,可以分为生成式攻击和搜索式攻击.生成式攻击是指通过策略一次生成一条攻击序列,随机攻击和度数攻击、介数攻击等就是此类,因为是一次生成所以计算成本较低,但是效果依赖于生成策略;搜索式攻击是指遍历多条攻击序列,以启发式方法寻找最优的序列,因为要遍历多条攻击序列所以计算成本较高,但是效果较好.
攻击节点序列问题比攻击节点集合问题更复杂,搜索式攻击计算成本较高,所以在网络攻击研究中,针对节点集合的搜索式攻击应用较多,而在攻击节点序列问题上以生成式攻击为主,搜索式攻击的应用较少且应用的网络大小较小.如在攻击节点集合问题上,Deng等[19]将网络攻击问题转化为二进制整数规划问题,使用禁忌搜索加贪心策略来寻找关键节点集合,这里的关键节点,是指对保持网络连接性的最重要节点.实验表明,该策略可以提高网络解体的效果,但是计算成本也非常高.Lozano等[20]针对最小化最大介数问题(The Min-Max Betweenness Centrality Problem),改进了人工蜂群算法,探索邻域中有益信息,并对已知解进行部分破坏和启发式重构.Li等[21]针对关键节点集合问题使用基于邻域信息的概率算法搜索最小关键节点集合.在攻击节点序列问题上,孙昱等[22]使用禁忌搜索方法查找最优攻击序列,但所涉及的网络最大仅为53个节点.
生成式攻击计算成本较低,但是攻击效果依赖于生成攻击序列的策略,搜索式攻击遍历多条攻击序列进行搜索,效果较好但是计算成本高.通过分析小规模网络上搜索式攻击得到的最优攻击序列的性质,可以促进生成式攻击的研究,并指导复杂网对抗攻击性能的研究和优化.本文使用遗传算法求解复杂网络的最优攻击序列问题,然后对得到的攻击序列进行特征分析.发现遗传算法求得的攻击序列所选的节点更多的利用了破坏性特征,其节点度数排名更靠后,并且在不同类型的网络上,不同特征的重要程度不一样.
2 复杂网络能控性鲁棒性最优攻击序列问题
2.1 复杂网络的能控性
复杂网络的能控性的概念由R.E.卡尔曼在1960年提出[23],是指在有限的时间内,通过控制输入驱动网络从初始状态到达目标状态的能力,需要的控制输入越多,其能控性越弱,需要的控制输入越少,其能控性越强.通常,能控性可由控制节点的密度(nD)来衡量:
(1)

控制节点数ND可以根据结构能控性[1]或精确能控性(exact controllability)[24]计算.结构能控性下控制节点数可以依据最小输入理论(minimum inputs theorem)[1],可由最大匹配计算得到:
ND=max{1,N-|E*|}
(2)
其中E*代表在网络中存在的最大匹配,|E*|是该最大匹配的大小,|E*|可由匈牙利算法得到.
2.2 能控性鲁棒性
能控性是衡量网络可控制能力的静态属性,能控性鲁棒性则是网络在攻击过程中表现出来维持能控性的动态属性.一个网络在攻击过程中能控性鲁棒性的定义如下:
(3)
其中ND(i)表示当去除i个节点后,网络所需的控制节点的个数;N-i为去除i个节点后的网络剩余节点数,该式定义了攻击下能控性下降的动态过程.而能控性鲁棒性的度量如下:
(4)
较小的R值表示具备较好的能控性鲁棒性.
2.3 网络攻击
本文所指网络攻击,是指按某种顺序去除网络中的节点,这个顺序即为攻击序列.其过程如下:
以邻接矩阵A(G)=(aij)N×N表示网络G(V,E).其中V代表网络中的节点集合,E代表网络中含有的连边集合.aij为矩阵中的元素,aij=1表示第i个节点到第j个节点之间有一条有向边.对网络第k个节点的攻击在邻接矩阵中的表示为:
A(k,:)←[]andA(:,k)←[]
(5)
2.4 攻击序列优化模型
针对结构能控性鲁棒性的网络最优攻击序列问题可以描述为:
(6)
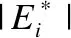
一个攻击序列X=[x1,x2,…,xn]表示在n个节点的网络中去掉节点的顺序为x1→x2…→xn,攻击序列中的节点的序号不能重复.
寻找复杂网络的最优攻击序列是一个最大优化问题,式(6)中,R(X)的范围在[0,1]之间.为便于求解,本文将其转换为最小化问题,即适应度函数为:
f(x)=1-R(x)
(7)
3 基于遗传算法求解攻击序列
3.1 序列重复的问题
在使用路径表示编码时,使用两点交叉和随机变异等一般的交叉和变异算子,序列中会出现重复节点.一种有效的处理方法为随机替换法,将重复的节点随机替换为未出现的节点.该种方法相当于对攻击序列进行了变异,增加了随机性.在攻击复杂网络的过程中,是按照攻击序列的顺序依次去除节点的,所以优先级更高的节点会出现得更早.对于在交叉中出现的重复项,替换掉先出现的重复项可能会破坏序列前面有效的序列结构,所以对重复节点的处理按照序号倒序进行的.对于在变异中出现的重复项,为了降低替换重复项时的随机性对真实变异率的影响,应优先替换后面的重复项.所以,对一个攻击序列去掉重复项的方法如下:
对一个序列从后往前依次检查,如果有重复项,则随机替换为未在序列中出现的一个序号.在交叉和变异阶段攻击序列可能会出现重复项,而变异在交叉之后,所以在变异之后进行节点序号纠正.对含有重复项的序列“5,3,4,1,5,1”进行去重复的过程见图1.
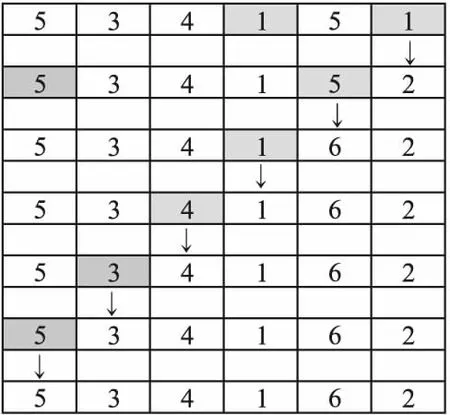
图1 攻击序列的节点序号的纠正方法示例
3.2 使用的遗传算法
遗传算法最初是为了研究自适应系统而发展起来的,具有非常广泛的使用场景.虽然近年来出现了许多进化算法,但是遗传算法依然流行,因为它简单易实现,具有高效、并行等特点,在各种问题上也都表现出很好的性能.本文使用的遗传算法(Generation Algorithm,GA)见表1.

表1 GA算法
随机生成种群作为父代种群,然后开始迭代寻优:计算种群中个体的适应度,记录下全局最优的个体,然后选择当前适应度最强的个体作为第1个父代,使用随机遍历采样选择第2父代(不和第一个父代相同),和第一个父代交叉生成子代,对子代进行变异,当子代种群个数和父代种群个数一样时结束交叉变异(表1中第7步的|Children|<|Parents|表示子代种群的个体数量小于父代种群的个体数量),对得到的子代进行攻击序列节点序号纠正处理,将得到的子代作为父代进行下一次迭代(Parents←Children),直至满足终止条件.
4 数值实验
4.1 实验网络
采用以下网络生成方法生成有向网络用于实验,使用平均度来控制网络的连边数量.
4.1.1 随机网络(ER)
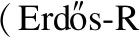
1.初始化:从N个孤立节点开始.
2.遍历所有可能的连边,以等可能概率pRG∈[0,1]连接连边.从i~j和j~i的概率相等.
从统计学上讲,期望的边数为E(M)=pRGN(N-1)/2.为了精确的控制边数M,可以均匀随机添加或删除边,其中添加边时,方向可以是随机的.
4.1.2 无标度网络(SF)
现实中的很多网络都不是随机生成的,而是具有偏好连接性质,即“富者愈富”,连接数越多的节点越有可能被连接,这就是无标度网络(Scale-Free network)[26].
1.初始化:从N个孤立节点开始.
2.给节点i分配权重wi=(i+θ)-σ,σ∈[0,1)andθ< 3.两个节点i和j(i≠j,i,j=1,2,…,N)从池中随机抽取,其概率分别与权重wi和wj成正比.然后,令Aij=1,即把节点i、j连起来 . 4.重复步骤3,直到添加M条边. 4.1.3 QSN网络 QSN(Q-snapback network)[27,28]模型类似于工业装配线自动化,它依赖一个带有回跳边缘的主链,从而产生一个多环结构.当QSN网络的层数为1时,这个QSN的生成方式: 1.初始化:从N个节点的有向链开始.其中每个节点i(i=1.2,…,N)有一条边Ai,j+1. 2.对于每个节点i=rQSN+1,rQSN+2,…,N,以概率q∈[0,1]向后连接到之前出现的节点j=i-l×rQSN(其中l=1,2,…,⎣i/rQSN」.这一步会形成一个j→j+1→…→i→j的有向环.rQSN控制某一个节点向前连接时间隔的节点数. 4.1.4 随机三角网络(RTN)[7] 多环结构有利于可控性的鲁棒性和网络稳定性[29].三角结构在现实生活中也经常被观察到.因此,本文设计一个有向随机三角形网络,如下: 1.初始化:从N-3个孤立节点开始,其他3个节点链接成一个有向环. 2.随机选取两个节点i和j,不带边Aji或Aij.然后,从所有的j的邻居中选取节点k,如果有一条边Ajk,则添加两条边Aij和Aki;否则(边为Akj),添加两条边Aji和Aik. 蓄意常见的攻击方式有基于破坏性、基于度数、基于介数等特征的攻击.使用遗传算法求解网络攻击序列问题属于搜索式攻击,目前未见针对复杂网络能控性鲁棒性的搜索式攻击方法,所以对比以下传统攻击方法: 1)Rand(Random Attack):随机攻击,在攻击过程中,每一次攻击时随机选择一个节点. 2)Tdeg(Targeted out-degree attack):基于度的攻击,每次攻击度数最大的节点,如果最大度数的节点有相同几个,则选择其中介数最大的一个.本文中针对有向网络节点度均的计算均使用出度. 3)Tbet(Targeted betweenness attack):基于介数的攻击,每次攻击介数最大的节点,如果最大介数的节点有相同几个,则选择其中度数最大的一个. 4)Tgreedy(Targeted greedy attack):贪心攻击,每次攻击破坏性最大的节点,即使得网络能控性下降最多的节点,如果最大破坏性的节点有相同几个,则选择其中介数最大的一个. 5)HD(Hierarchical out-degree-based attack)[18]:基于节点度的层级攻击,依照节点删除后驱动节点数量变化情况将节点分类为关键节点,普通节点和冗余节点三种层级.在每一次攻击时,若存在关键节点则选择关键节点进行攻击,否则选择普通节点,若普通节点也不存在,则选择冗余节点.在每一个层级中选择度数最高的节点进行攻击.层级攻击本质上是基于破坏性的攻击,它和Tgreedy的区别在于评价破坏性时考虑到了驱动节点和不匹配节点,并进行了层级划分. 6)HB(Hierarchical betweenness attack)[18]:基于节点介数的层级攻击.层级选择同HD,在每一个层级中选择介数最高的节点进行攻击. 实验环境:仿真软件为MATLAB R2018a,处理器为AMD Ryzen 7 5800X 8-Core,安装内存为128GB.运行系统为Ubuntu 20.04LTS. 实验方式:5种攻击方式分别对4种类型的生成网络进行攻击,每种网络随机生成24次. 网络参数:节点数:N=100,平均度:[2,15]区间内的所有整数. 遗传算法参数(通过正交实验确定):种群:Popsize=300,变异率:Pc=0.05,交叉率:Pm=0.9,终止条件:评价次数≥150000次. 4.4.1 平均度为2和7的网络上的结果 图2 攻击结果 图3 攻击结果 表2和表3中加粗字体表示该行中最小的R值,即在该种攻击方法下能控性鲁棒性最好的网络;灰色字体表示该行中最大的R值,即在该种攻击方法下能控性鲁棒性最差的网络;灰色背景表示该列中最大的R值,即在该网络上攻击效果最好的方法.可见GA得到的结果最优.在 表2 表3 4.4.2 在平均度变化的情况下的结果 图4是在网络平均度变化下的情况下,各个攻击方法得到的各网络R值的变化情况.可见,随着网络平均度的增加,各方法得到的R值都越来越低,这是因为随着平均度的增加,网络中的连边增多,网络的能控性鲁棒性越来越强,攻击难度也越来越大. 图4 平均度变化时各方法得到的R值变化(网络节点数N=100) 图5是在网络平均度变化下的情况下,在各类网络上攻击方法攻击效果的排名变化情况,除了 图5 各种攻击方法在各种网络上的攻击效果在不同平均度下的排名(网络节点数N=100) 4.4.3 图6 GA在4种网络上得到的节点的特征分析(网络节点数N=100) 由图可知,GA得到的攻击序列上的节点的度和介数排名波动较大且较为靠前,而其破坏性排名极为靠前,可见对于复杂网络的能控性鲁棒性攻击序列的攻击效果来说,每一次攻击时节点的破坏性是一个重要特征.其控制节点数增加主要集中在前期和中期,到后期控制节点数不再增加,因为此时所剩下的节点都是孤立节点,所以每个节点都是驱动节点. 4.4.4 平均度变化时攻击序列特征分析 为了研究在网络平均度变化的情况下各方法得到的攻击序列的特征变化,将攻击序列上的节点在每一次攻击之后的特征相对排名取平均,然后观察在平均度变化的情况下,各个方法攻击序列特征相对排名的变化. 图7为在网络平均度变化的情况下各方法得到的攻击序列上节点的度的平均排名情况.曲线上的点表示在对应的 图7 攻击序列上节点的度的相对排名变化(网络节点数N=100) 从Trand(随机攻击)的情况中可以得到网络中的节点排名变化的基本趋势,随着 图8为在网络平均度变化的情况下各方法得到的攻击序列上节点的介数的平均排名情况.曲线上的点表示在对应的 图8 攻击序列上节点的介数的相对排名变化(网络节点数N=100) Trand得到的结果显示,随着平均度的增加,在攻击过程中随机选择一个节点其介数排名越来越靠后.在ER网络上,GA的介数排名在Tdeg、HD和Tgreedy、HB之间,且与Tdeg、HD接近,Tgreedy方法得到的攻击序列上的节点的介数排名都靠前,这是因为本文所采用的Tgreedy方法在破坏性排名最大的节点有多个时会选择其中介数最大的一个,HB方法在每一个层级中进行选择时会选择其中介数最大的一个.在SF、RTN上,GA的介数排名比Tdeg、Tgreedy、HD、HD靠后.在QSN上Tdeg、HD的介数排名比GA靠后. 图9为在网络平均度变化的情况下各方法得到的攻击序列上节点的破坏性的平均排名情况.曲线上的点表示在对应的 图9 攻击序列上节点的破坏性相对排名变化(网络节点数N=100) Rand得到的结果显示,随着平均度的增加,在攻击过程中随机选择一个节点其破坏性排名越来越靠前,这是因为当连边越多的时候越容易出现大多数节点破坏性相同的情况.在所有网络上,破坏性排名都呈现出Rand>Tdeg>Tbet>GA的情况,并且GA在各网络上得到的攻击序列的破坏性排名均非常靠前. 网络的最优攻击序列问题是一个NP-hard问题,现有的研究多关注于生成式攻击,因为计算成本的问题,启发式搜索更多用于攻击节点集合问题,用于攻击序列问题较少.本文使用遗传算法求解复杂网络能控性鲁棒性最优攻击序列问题,在节点数为100的网络上的实验结果说明GA得到的攻击序列相比于对比算法是最优攻击序列;然后分析了在网络平均度变化的情况下GA所求得的最优攻击序列和其他方法得到的攻击序列的特征,发现在所用网络上,相比于其他蓄意攻击方法,GA方法得到的最优攻击序列的节点度数排名更靠后,且破坏性排名靠前;随着网络平均度的增加,GA方法得到的最优攻击序列的节点度数排名会随着网络平均度的增加而增加(靠后)、且比其他方法的结果更靠后;除了QSN网络之外,介数排名变化比度数排名变化平缓;即使在网络平均度增加的情况下,GA方法得到的最优攻击序列的节点破坏性排名均极为靠前. 这说明在ER、SF、RTN这3种网络的能控性鲁棒性最优攻击序列问题上,对于GA求得的最优攻击序列来说,按特征的重要程度排序:破坏性特征>介数特征>度数特征;而对于QSN网络,则是破坏性特征>度数特征>介数特征.在未来可以引入更多的特征分析进行研究.4.2 对比攻击方法
4.3 实验环境与实验设置
4.4 实验及实验结果
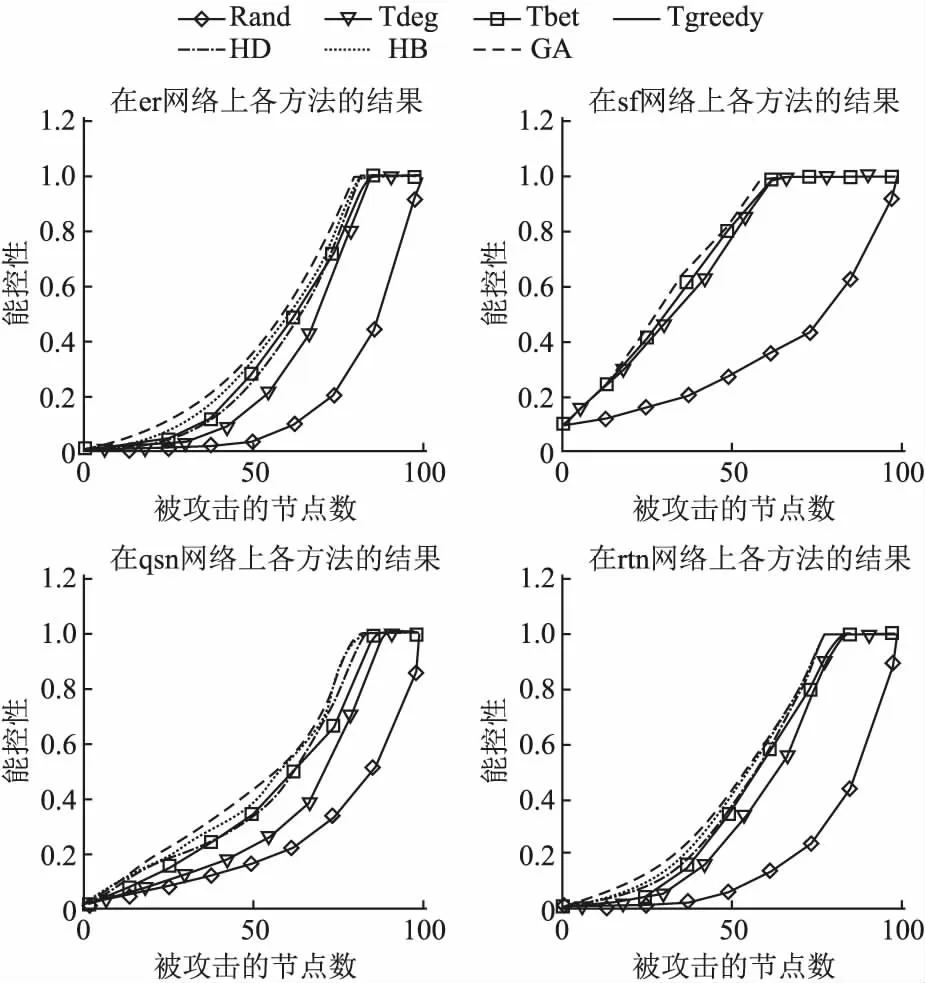
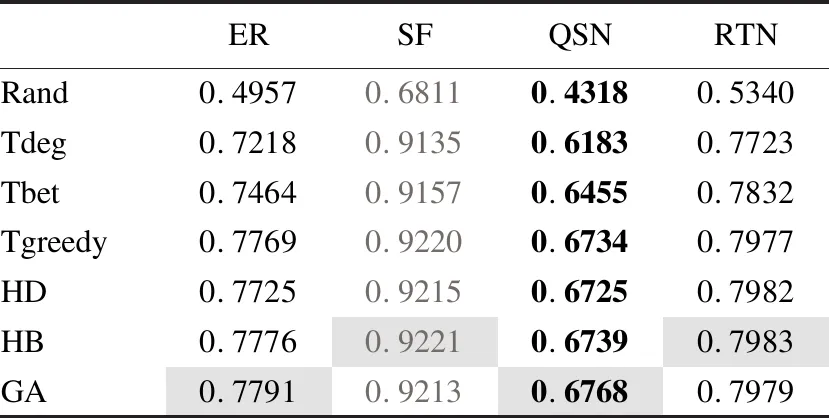
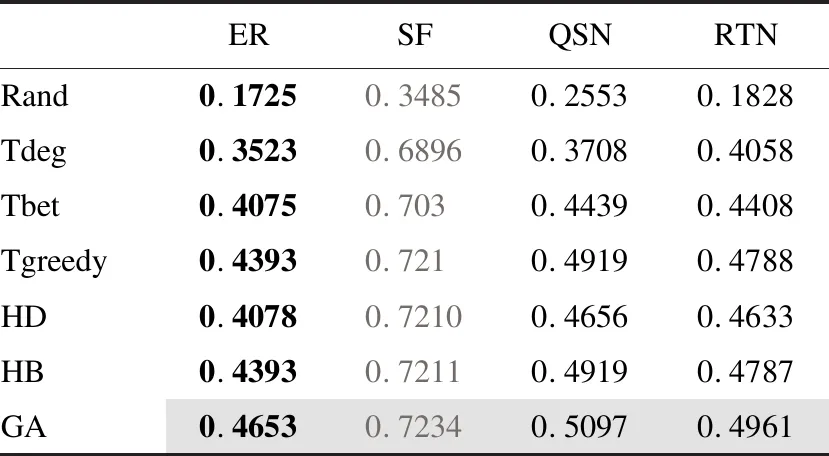
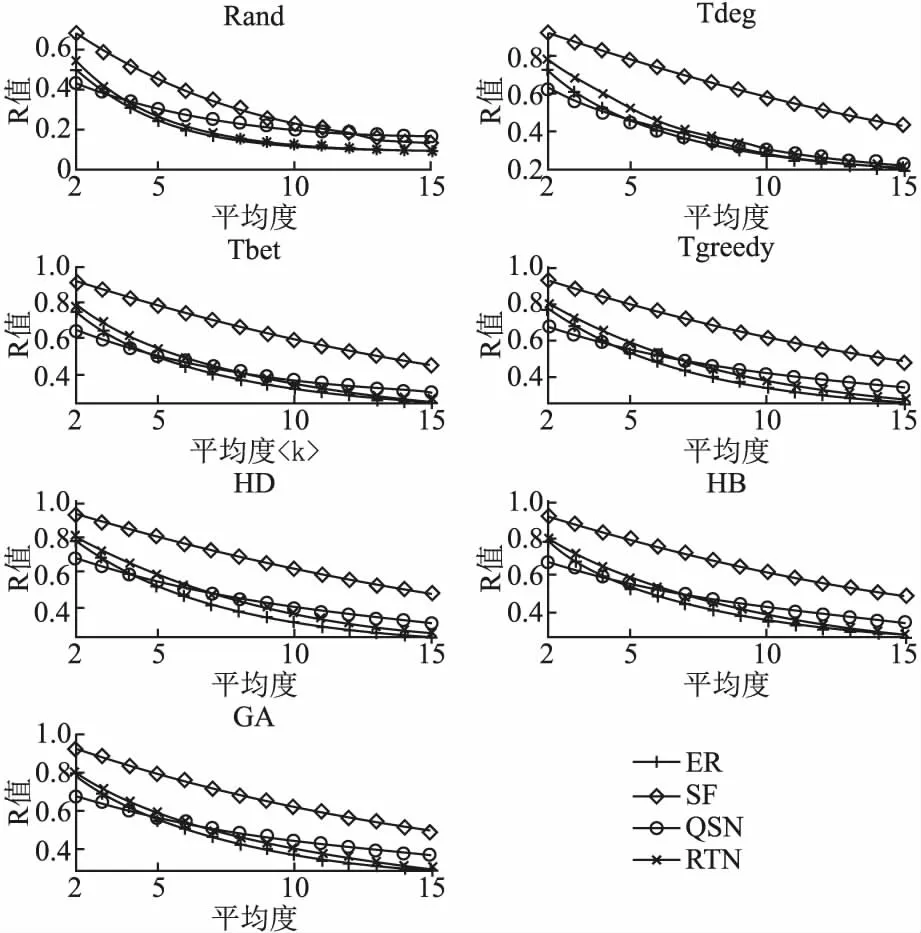


5 结 论

