基于三支决策的证据融合策略
陈 缘,王加阳
(中南大学 计算机学院,长沙 410083)
1 引 言
随着海量不确定性数据出现,如何处理并探寻这些数据中蕴含的知识已成为一个热点课题.证据理论的提出和发展[1,2]丰富了处理不确定性问题的方法,在智能决策、目标优化、故障检测和统计分析等领域发挥了不可替代的作用[3-7].证据合成是证据理论的重要部分,对于来源不同的证据,往往因其主要支持的焦元不同而产生冲突.当证据之间存在冲突时,直接使用D-S规则进行合成常会产生证据悖论[8-10].针对这一问题,许多学者对冲突证据合成方法进行了大量研究和改进,这些方法大致可分为以下两类:
一类是对组合规则进行修正,由此产生了许多新的组合规则.其中有的学者在改进的组合规则中考虑如何分配冲突量[11-13].Wang等[14]对相似性碰撞进行分析和说明,并提出一种新的组合规则.Du等[15,16]提出依赖于主客观的的广义组合规则.但这些组合规则可能会破坏交换律和结合律等数学特性,当待融合的证据较多时,结果可能会有较大偏差.
另一类是对证据源进行修正,关键在于如何确定证据的折扣系数.通常是通过度量证据不确定性,以及计算证据相似系数、证据距离等来确定折扣系数.Jousselme等[17]通过幂集空间上的序列向量计算证据距离;Yu等[18]定义了一种支持概率距离,以证据的被支持度确定其折扣系数;陈哲等[19]通过构建冲突关系网络,利用PageRank算法来修正证据权值;Xiao[20]通过衡量证据的各种可信度来修正权重;Xiong[21]等通过研究证据网络中节点的直接和间接互动来实现权值修正.但上述方法或多或少存在局限性:有的方法简单地将证据之间的关系分为冲突和不冲突两种,可能会出现划分错误的情况;有的方法在处理高冲突证据时能够取得很好的合成效果,但当合成证据彼此冲突较小时,可能会引入不必要的计算量.究其原因,在于前者对于介于冲突和不冲突之间的证据关系没有进行深入的探讨,仅通过人为确定的单一阈值无法对证据间的复杂关系进行确切区分.后者则无法有效判断证据是单类还是多类[22],在融合单类证据时有杀鸡牛刀之嫌,无法避免其过程复杂和计算量大的缺陷.
三支决策模型[23,24]作为对传统二支决策的推广和拓展,通过引入延迟决策的概念来规避当前因为可用信息不足带来的风险[25],在数据采样、自动聚类等方面[26,27]得到了实际应用.利用三支决策模型,能够更好地对证据之间的冲突和一致性进行说明,并可以为证据的划分提供理论支持.为此,本文提出一种基于三支决策的证据融合策略,来实现证据冲突的分而治之.该策略能够根据证据的焦元特征快速辨别证据关系,进而根据冲突大小采用不同的合成态度和策略.并通过证据集来合并具有一致性的证据,避免了传统方法中对证据距离或关系的逐次比较.与现有方法相比,本文方法采用更为灵活变通的方式来融合证据,在充分利用证据信息的情况下能够减少计算量,为证据融合方法提供一种新的思考角度和方式.
接下来,本文将概述证据理论和三支决策的相关知识,并分析如何应用三支决策思想去看待证据之间的冲突关系,在此基础上提出基于三支决策的证据融合策略:首先确定每个证据支持的主要焦元,从支持的焦元是否相同的角度看待证据与证据集关系,构建三支决策证据关系模型将证据划分到对应的证据集中或边界上.接着,对证据集内部的证据使用D-S规则合成,对证据集的合成结果和边界证据使用不同的规则进行权值修正,然后统一进行合成.最后,结合多源证据融合实例,与其他融合规则进行对比分析,来说明本文方法的有效性.
2 相关概念
2.1 三支决策模型
Yao[23,24]基于贝叶斯最小风险理论和决策粗糙集理论,提出了三支决策模型:给定一个S=
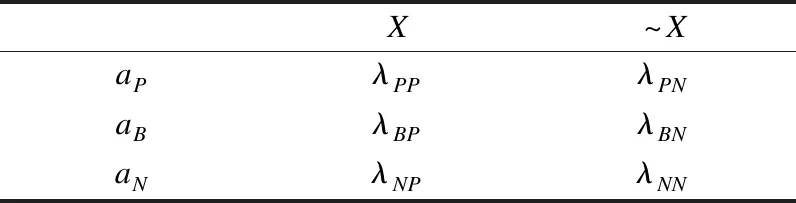
表1 不同行动的代价函数
如表1所示,当一个对象属于集合X时,采取动作aP,aB,aN对应的代价分别为λPP,λBP,λNP;当一个对象不属于集合X时,采取动作aP,aB,aN对应的代价分别为λPN,λBN,λNN.当一个对象属于集合X时,代价函数通常满足:λPP≤λBP<λNP,它说明将一个属于X的对象x划分到正域POS(X)的代价要小于或等于将其划分到边界域BND(X)的代价,而这二者的代价都小于将其划分到负域NEG(X)的代价.同理,当一个对象不属于集合X时,代价函数通常满足:λNN≤λBN<λPN.
使用P(X|[x]R)表示对象所在的等价类[x]R属于集合X的条件概率,它的计算公式为:
(1)
对于一个对象x,采取行动aP,aB,aN的期望代价为:
R(aP|[x]R)=λPPP(X|[x]R)+λPNP(~X|[x]R)
(2)
R(aB|[x]R)=λBPP(X|[x]R)+λBNP(~X|[x]R)
(3)
R(aN|[x]R)=λNPP(X|[x]R)+λNNP(~X|[x]R)
(4)
根据贝叶斯最小风险决策理论,可得最小代价决策规则如下:
(P)如果R(aP|[x]R)≤R(aB|[x]R),且R(aP|[x]R)≤R(aN|[x]R),则x∈POS(X)接受决策.
(N)如果R(aN|[x]R)≤R(aB|[x]R),且R(aN|[x]R)≤R(aP|[x]R),则x∈NEG(X)接受决策.
(B)如果R(aB|[x]R)≤R(aP|[x]R),且R(aB|[x]R)≤R(aN|[x]R),则x∈BND(X)接受决策.
2.2 证据理论
定义1[1,2].设Θ为识别框架,基本信任分配函数m是一个从集合2Θ到 [0,1] 的映射,A表示识别框架Θ的任一子集,记作A⊆Θ,且满足:
(5)
定义2[1,2].假定识别框架Θ下的两个证据E1和E2,其相应的质量函数为m1和m2,焦元分别为Ai和Bj,使用D-S合成规则后合成的质量函数为:
(6)
式中:
K=∑Ai∩Bj=Øm1(Ai)m2(Bj)
(7)
它反映了各个证据之间的冲突程度,系数1/(1-K)称为正则化因子.由m给定的质量函数称为m1和m2的正交和,记作m1⊕m2.
定义3[19].假设证据的权重为w,则对证据进行加权修正后的质量函数为:
(8)
其中,m(Θ)表示对整个识别框架分配的质量函数,m(A)表示对任一焦元分配的质量函数.
定义4[28].假设识别框架上Θ的证据质量函数为m,则Pignistic概率转化函数BetPm满足:
(9)
其中|B|为集合的基数大小,A为单点集,BetPm将复合集焦元的信度平均分配给了其包含的单点集焦元.
3 基于三支决策的证据关系模型
当多个证据进行合成时,证据冲突产生的主要原因是不同的证据支持不同的焦元,而传统D-S规则无法有效处理证据之间的高冲突,只适用于冲突相对较小的证据融合.但是在如何界定证据之间的高低冲突这一问题上,已有文献提出的方法常常通过对冲突量设置阈值来区分,可能出现划分错误的情况,缺乏对证据冲突的边界的深入分析和讨论.证据之间的冲突关系不应简单地概括为“冲突”和“一致”两种,介于“冲突”和“一致”之间的关系同样值得讨论:这说明证据之间既存在无法避免的冲突,也存在不可忽视的一致性.换而言之,证据之间可以保持“中立”关系.
3.1 模型的建立
证据的合成结果本质上是证据在不同焦元上的拉锯,当证据支持的焦元趋向于一致时,对应的冲突也就越小,因而可从证据支持的焦元集合是否相同来判定证据之间的关系.
假设识别框架Θ={x1,…,xn},构造状态集合AC={aU,aN,aC}来分别表示3种证据关系:一致的(Uniform),中立的(Neutral)和冲突的(Conflicting),E表示当前证据支持的焦元集合,~E表示当前证据不支持的焦元集合,~E是E在识别框架Θ上的补集.证据与当前证据支持的焦元集合E一致时,判定证据关系aU,aN,aC对应的代价分别为λUU,λNU,λCU;证据与当前证据支持的焦元集合E不一致时,判定证据关系aU,aN,aC对应的代价分别为λUU,λNU,λCU.综上,在不同条件下对证据的不同关系进行判定的代价如表2所示.

表2 判定证据不同关系的代价函数
值得注意的是,代价函数需满足:λUU≤λNU<λCU,它说明将一个与E一致的证据划分到一致域UNI(E)的代价要小于或等于将其划分到中立域NEU(E)的代价,而这二者的代价都小于将其划分到冲突域CON(E)的代价.同理,后者的代价函数需满足:λCC≤λNC<λUC,它说明将一个与E冲突的证据划分到冲突域CON(E)的代价要小于或等于将其划分到中立域NEU(E)的代价,而这二者的代价都小于将其划分到一致域UNI(E)的代价.
同时,记P(e,E)为证据e与当前证据支持的焦元集合E一致的概率,记P(e,~E)表示证据e与当前证据支持的焦元集合E不一致的概率,也即e与焦元集合~E一致的概率.结合表2,判定证据e与当前证据支持的焦元集合E的证据关系时,采取行动aU,aN,aC的期望代价分别为:
R(aU)=λUUP(e,E)+λUCP(e,~E)
(10)
R(aN)=λNUP(e,E)+λNCP(e,~E)
(11)
R(aC)=λCUP(e,E)+λCCP(e,~E)
(12)
根据贝叶斯最小风险决策理论,可得最小代价的行动规则如下:
(U)如果R(aU)≤R(aN)且R(aU)≤R(aC),则采取行动aU,认为证据之间是一致的.
(C)如果R(aC)≤R(aN)且R(aC)≤R(aU),则采取行动aC,认为证据之间是冲突的.
(N)如果R(aN)≤R(aU)且R(aN)≤R(aN),则采取行动aN,认为证据之间是中立的.
3.2 一致概率的计算
当多个证据进行合成时,其合成结果可以看作是它们在焦元上的拉锯和博弈,所以问题的关键在于如何确定各个证据支持的主要焦元.而证据间的一致性也表现在它们对各个主要焦元的支持度,同时应忽略非主要焦元的影响.
首先为得到证据e支持的主要焦元集为FSe,需要区分证据的主要焦元,而非焦元.此时需要考虑两个方面的问题:其一是避免质量函数过小的焦元被误判为主要焦元,其二是为使集合形式更为精简,需要将复合集焦元的信度平均分配给单点集焦元.下面通过两个例子说明这两个问题的必要性.
例1.假设识别框架Θ={A,B,C,D},某个证据的质量函数为:m({A})=0.3,m({B})=0.3m({A,B})=0.3,m({C})=0.05,m({D})=0.05.可以看出证据对{C}和{D}的相对信任度比较小,故{C}和{D}不应纳入主要焦元的范畴,即避免质量函数过小的焦元被当成主要焦元.
例2.假设识别框架Θ={A,B,C,D},某个证据的主要焦元集合FS={{A},{B},{A,B}},而当前证据集支持的主要焦元集为{{A},{B}},正因为复合集焦元的存在,难以考量二者的主要焦元的重叠部分该如何计算,若将复合集焦元的信度平均分配给单点集焦元,则有利于问题的简化,同时,主要焦元集合可能包含的元素个数将会从24个缩小到4个,且元素之间不重叠,更具有合理性.
因此,为避免复合集焦元对区分主要焦元的干扰,应先将对复合集焦元的信度平均分配给单点集焦元,即使用Pignistic概率转化函数实现复合集焦元到单点集焦元的转化,再尽量避免质量函数过小的焦元被误判为主要焦元.而大津法能够将数据分成两类,使它们的类间方差最大,这与区分主要焦元和非主要焦元的思想不谋而合,但是当数据差别不大时,大津法可能不会取得很好的效果.从另一方面来说,信度越大的焦元为主要焦元的可能性越大,而信度最大的焦元一定为主要焦元,可以通过信度之间的比值来确定其他的主要焦元.据此本文设计了以下算法来区分主要焦元.
算法1.区分证据主要焦元集合算法.
输入:识别框架Θ={x1,x2,…,xn},证据质量函数m.
输出:证据的主要焦元集合FS.
1.输入质量函数,并根据Pignistic概率转化公式计算BetPm(xi)的值,i=1,2,…,n.
2.在BetPm找到最大值max和非零最小值min.
3.如果max/min≥k,(k是常数,通常k≥3)则转到步骤 4 ;否则转至步骤 5.
4.设置区分主要焦元的阈值Th为min,并转至步骤 9.
5.对BetPm(xi),i=1…n从小到大排序,得到序列L={l1,…,ln},并计算它们的平均值avgΘ,并初始化j=1.
6.将序列L分为两类:L1={l1,…,lj},L2={lj+1,…,ln}.分别计算L1和L2的平均值avg1和avg2.根据公式[29]σ2=j(avg1-avgΘ)2+(n-j)(avg2-avgΘ)2计算此时的类间方差,并保留在数组var中第j个位置.
7.判断j和n的大小关系,若j 8.在数组var中寻找最大类间方差,以及它所对应的位置k,将Th设为lk. 9.对x1,x2,…,xn逐一比较BetPm(xi)和Th的大小,若BetPm(xi)>Th,则将xi加入到FS中. 10.算法结束,输出证据的主要焦元集合FS. 经典三支决策模型使用P(X|[x]R)来描述对象所在的等价类[x]R属于集合X的条件概率,但在基于三支决策的证据关系模型中,不宜继续使用条件概率,其主要原因有两个:1)条件概率本质上是描述在某一事件已发生的条件下另一事件发生的概率,而除时序证据之外,证据之间并无先来后到之说;2)证据关系是对称的,但条件概率的计算方式使其无法实现对称性.本文认为证据e与当前证据支持的焦元集合E的一致性表现在它们是否支持同样的焦元,同时应忽略非主要焦元的影响,故通过焦元集合之间的相似度[10]来计算二者一致的概率,即: (13) 式中FSe表示证据e支持的主要焦元集合. 对证据关系进行不同的判定会有对应的代价,判定结果更符合证据之间关系的本质,代价则越小,反之,代价则越高. 当证据e支持的主要焦元集FSe与当前证据支持的主要焦元集合E越接近时,可以认为二者的一致性越高,而认为二者一致的代价也就越小.问题的关键转化为如何确定集合之间的距离. 定义5.在识别框架Θ={x1,x2,…,xn}上,使用向量V={v1,v2,…,vn}来表示证据支持的焦元集合,当vi=1表示证据支持第i个焦元,反之当vi=0表示不支持. 由此,集合之间的距离可以转化为向量之间的距离,本文使用欧式距离来计算集合距离d(FSe,E): (14) (15) (16) (17) (18) (19) (20) 事实上,不同的证据关系正对应了不同的融合态度,应而可采取不同的融合策略.例如当判定证据关系为aU,可以采用相对简单的融合策略来提高融合效率;当证据关系为aC时,说明证据之间不宜直接进行融合. 当证据关系为aU时,证据的融合规则应满足交换律和结合律,这样当多个具有一致性的证据进行融合时,证据融合的先后顺序不会影响最后融合的结果.同时,因为此时待融合的证据倾向于支持相同的焦元,证据的融合规则应尽可能简单,使得计算速度尽可能快.D-S组合规则满足交换律和结合律,同时运算规则较简单,可作为此时的融合备选方案. 当证据关系为aC时,比较激进的策略是不予以融合,例如在时序证据融合过程中常会舍弃与当前证据存在高冲突的证据.其他的策略可选择对冲突证据进行加权修正后再进行融合,若无法确定孰轻孰重,可各分配1/2的权重. 当证据关系为aN时,表明证据之间存在一致性同时也存在不可忽略的证据冲突,当前可用信息不足,可暂缓融合过程,待更多证据加入后再进行融合.若必须进行融合,可根据证据本身的不确定性或其他特性来修正权重再进行融合. 上一节中本文对基于三支决策的证据冲突情况进行了分析,把证据之间的关系分为一致、中立和冲突三种.当有多个证据进行融合时,如何根据证据的关系,采取不同且合适的合成策略是本文研究的重点.为此,本文提出了基于三支决策的证据融合策略:首先根据各个证据支持的主要焦元确定初始证据集上的焦元分布.接着应用基于三支决策的证据关系模型来判断证据与各初始证据集的关系.当证据与某初始证据集为一致关系时,将其划分到证据集内部;为中立关系时,划分到证据集边界上;为冲突关系时,划分到证据集外部.通过将证据划分到不同证据集内部或边界来确定其权重,最后对加权证据进行融合. 多个证据中可能存在支持相同主要焦元的证据,这些倾向于支持同样焦元的证据便组成了证据集.当需要融合多个证据时,大部分证据源修正改进法需要逐一计算证据两两之间的某种距离或关系,而本文方法使用证据集来合并具有一致性的证据,将证据与证据的关系转化为证据与证据集的关系:证据可能属于某一证据集,也可能与证据集保持中立,而证据集之间彼此冲突.这种转化的关键在于如何确定初始证据集及其焦元分布. 沿用前节3.2中的算法1,可得单个证据的主要焦元.当多证据融合时,便可根据这些证据的主要焦元确定初始证据集,进而利用证据集归并具有一致性的证据.为此,本文设计了如下算法来确定初始证据集上的焦元分布. 算法2.确定初始证据集上的焦元分布. 输入:m个证据的主要焦元集合FS1,…,FSm. 输出:n个证据集的集合ES={ES1,…,ESn},ESi为第i个证据集. 1.初始化i=1,n=1,ES={FS1}. 2.i=i+1,并判断FSi∩ES的交集是否为空,若为空则n=n+1,并令ESn=FSi,将ESn加入至ES中;否则转至步骤4. 3.判断FSi∈ES是否成立,若成立,则转至步骤2;否则设j=1并转至步骤4. 4.判断j≤n是否成立,若成立转至步骤5;否则令ESn+1=FSi,n=n+1并转至步骤2. 5.判断FSi=Ø是否成立,若成立则转至步骤2;否则转至步骤6. 6.判断ESj∩FSi≠Ø是否成立,若不成立则直接转至步骤7;否则令ESn+1=ESj-ESj∩FSi,n=n+1,并令ESj=ESj∩FSi,FSi=FSi-ESj,再转至步骤7. 7.j=j+1,并转至步骤4. 8.判断i和m的大小,若i≤m,则转至步骤2;否则转至步骤9. 9.算法结束,输出ES1,…,ESn. 由上述算法2可得初始证据集上的焦元分布.由于各个初始证据集包含的焦元并不重叠,可认为证据集之间彼此冲突.值得注意的是,此时得来的初始证据集内部证据数量为空,并不包含任一证据.因而需要进一步判断各个证据与初始证据集的关系,以此作为划分的依据. 得到初始证据集上的焦元分布之后,便可根据第3节的基于三支决策的证据关系模型来判定每条证据与证据集的关系,以此作为证据划分到证据集时的依据,即:当判定证据与证据集为一致关系时,将该证据分配到证据集内部;判定为中立关系时,将该证据划分到证据集边界上;判定为冲突关系时,则不予划分. 假定识别框架Θ={x1,…,xn},第i条证据的主要焦元集合为FSi,第j个证据集支持的焦元集合为ESj,同样构造集合AC={aU,aN,aC}来分别表示证据与证据集的3种关系:一致、中立和冲突.当证据与证据集存在一致关系时,判定证据关系aU,aN,aC对应的代价分别为λUU,λNU,λCU;存在冲突关系时,判定证据关系aU,aN,aC对应的代价分别为λUC,λNC,λCC. 沿用前节3.1中的建模过程,判定第i条证据ei和第j个证据集的关系时,采取行动aU,aN,aC的期望代价分别为: R(aU)=λUUP(ei,ESj)+λUCP(ei,~ESj) (21) R(aN)=λNUP(ei,ESj)+λNCP(ei,~ESj) (22) R(aC)=λCUP(ei,ESj)+λCCP(ei,~ESj) (23) 式中P(FSi,ESj)表示证据ej和第j个证据集的一致概率,通过式(13)计算而来.~ESj为ESj在识别框架Θ上的补集.λUU,λNU,λCU,λUC,λNC,λCC的计算则参照式(15)~式(20). 根据贝叶斯最小风险决策理论,可得最小代价的行动规则如下: (U)如果R(aU)≤R(aN)且R(aU)≤R(aC),则认为证据与证据集之间存在一致,将第i条证据分配到第j个证据集内部. (C)如果R(aC)≤R(aN)且R(aC)≤R(aU),则认为证据与证据集保持中立,将第i条证据划分到第j个证据集边界上. (N)如果R(aN)≤R(aU)且R(aN)≤R(aC),则认为证据与证据集存在冲突,将第i条证据分配到第j个证据集外部,也即不予划分. 当证据被分配到某一证据集内部时,由于证据集之间彼此冲突,可认为该证据与其他证据集也存在冲突;当证据被划分到某一证据集边界上时,它可能同样处于其他证据集的边界上. 假设总证据数量为k,若根据本文策略可划分为a个证据集ES1,…,ESa和b个边界证据E1,…,Eb.对于同一证据集内部的证据,因为它们之间存在较高的一致性,即证据冲突较小,故可以根据D-S规则直接进行合成,最后得到该证据集的合成结果.初始情况下可认为每个证据的权重均等,均为1/k,证据集内部的证据数量越多,说明它的相对可信度越大,也应具有更高的权重,故ESi的权重wi由该证据集的大小占总证据大小的比值来确定,即: (24) 对于划分到证据集边界上的证据,与之中立的证据集的权重有关,并由于被Ej划分到了证据集的边界上,因而分配原证据集的一半权重,同时应考虑它本身具有的权重,即: (25) 最后根据式(8)对证据集ESi和边界证据Ej进行修正,并使用D-S规则进行合成. 大部分证据源修正改进法对证据两两之间的距离或某种关联度进行衡量,进而获得距离矩阵,而本文方法与这些方法的主要区别在于以证据集为单位来判定证据关系.而其他方法与本文方法在最后权值修正和融合时所需要的计算量变化不大.因此,下面就生成距离矩阵和划分证据到证据集的计算量进行对比分析. 首先对传统的证据源修正法进行分析,以基于证据间相关系数的冲突证据合成方法[10](简称证据相关系数法)为例.假定待合成的证据数量为k,运算过程中的加减乘除、交并集、求基数和比较大小都视为一次运算.根据证据相关系数法中计算两个证据之间相关系数的公式,可知求解相关系数的计算量为: C1=CD+2n+2n·2n+2·(2n-1)+2n·2n+3=11×22n-1-3×n-1+1 (26) 式中:n表示识别框架Θ的基数大小,CD表示求解矩阵需要的计算量,文献[31]中给出了它的值为5×2n-1(2n-1).之后为了得到相似度矩阵,k条证据之间需要两两比较,则证据相关系数法的总计算量大小为: CS=k(k-1)C1=k(k-1)(11×22n-1-3×2n-1+1) (27) 接着对本文方法的计算量进行分析.据4.1节可知,确定初始证据集上焦元分布的计算量为: C2=7×2n×n+8n (28) 式中:n表示识别框架Θ的基数大小.根据证据集的焦元彼此不重叠的特性可知,最多可划分为n个初始证据集,此时每个证据集只支持单焦元.而划分证据到证据集时,需要对二者关系进行判定,每次判定需要的计算量为: C3=8n+26 (29) k条证据与n个证据集之间最多需要kn次比较.综合式(28)~式(29),可知本文算法的总计算量为: Cr=C2+knC3=7n·2n+8n(kn+1)+26kn (30) 综合式(26)~式(30),对证据相关系数法和本文方法的计算量进行对比,结果如图1所示.图中横坐标表示识别框架的基数大小,纵坐标为计算量大小(×108).曲线1~4从上至下分别为k=10,8,6,4时使用证据相关系数法的计算量,曲线5~8分别为k=10,8,6,4时本文方法需要的计算量.由图1可知,曲线5~8的增长速率明显低于曲线1~4,说明本文方法所需要的计算量远小于证据相关系数法.为了便于观察,对图1中纵坐标表示的计算量取自然对数lnC,如图2所示,可以看出证据相关系数法和本文方法的计算量的对数,都近似于线性增长. 图1 证据相关系数法与本文方法计算量图 图2 证据相关系数法与本文方法计算量的对数图 根据图1和图2可知,当证据的数量一定时,证据相关系数法和本文方法的计算量都随着识别框架基数增大而呈指数增长,但本文方法的增长速率更慢.当识别框架的基数一定时,二者的计算量虽然都随着证据数量的增多而增加,但本文方法的增长态势随证据数增多而变缓.主要原因在于本文方法的计算量CT主要集中在C2的指数部分,此时因证据数量变多而新增的计算量与这一部分相比可以相对忽略. 综上可知,较于经典的对证据源进行修正的改进方法,如证据相关系数法,本文方法能有效减少计算量.并且在识别框架的基数一定的情况下,当证据数量增多时,本文算法随之增加的计算量相对有限. 在疑难杂症的诊断中往往需要多个专家进行综合会诊.专家由于个人经验的不同可能会得出不同的诊断结果.此时可用证据的质量函数来表示诊断意见,但直接使用D-S规则对诊断意见进行融合,可能会得到有悖常理的结果进而造成医疗事故. 例3.假设在某次专家会诊中,病人被判断患上的疾病类型可分为A,B两种.其中,专家1判定患病类型为A的置信度为1,为B的置信度为0;专家2判定患病类型为B的置信度为1,为A的置信度为0. 该例中,因为两个专家的诊断意见完全冲突,无法根据D-S规则进行合成,又因此时证据冲突K=1而被称为全冲突悖论.根据常理,判断类型为A和判断类型为B的信度相同,即:0 例4.假设病人被判断患上的疾病类型可分为A,B,C这3种.其中,专家1判定患病类型为A和B的置信度分别为0.9和0.1; 专家2判定患病类型为B和C的置信度分别为0.1和0.9. 该例中,尽管两个专家对疾病类型B的信任度都很低,但使用DS规则合成后的结果对B的信度为1,明显不合理,被称为1信任悖论.根据常理,判断类型为A和判为C的信度相同,且均大于判为B的信度,即:0 例5.假设病人被判断患上的疾病类型可分为A,B,C这3种.其中,专家1判定患病类型为A和B的置信度分别为0.9和0.1;专家2判定患病类型为A、B和C的置信度分别为0.7、0.2和0.1;专家3判定患病类型为A、B和C的置信度分别为0.8、0.1和0.1;专家4判定患病类型为B和C的置信度分别为0.1和0.9. 该例中,若采取D-S规则进行合成,则合成结果为m(A)=0,m(C)=0,m(B)=1.无论其他专家对A和C的基本信任分配有多大,合成结果对A和C的基本信任分配均为0 ,被称为0信任悖论.而4个专家中对疾病类型为A的可信度普遍较高,其次是疾病C,最后是疾病B,因此合成结果基本合理的标准为:0 对上述算例采用相关算法进行合成.在此选择了Yager法[32]等其他合成方法,与本文方法进行对比,如表3所示.以此来说明本文方法能合理有效处理证据悖论. 表3 多种方法的冲突证据合成结果 由表3可知,经典DS规则无法有效处理证据悖论.Yager法处理以上3种悖论时分配了大量的信度给全集,合成结果对于决策缺乏实际意义.Murphy法能处理全冲突和1信任悖论,但在处理0信任悖论时分配了过多的信度给疾病类型A,存在不合理现象.基于证据相关系数的冲突证据合成方法和本文方法的结果都能符合3种悖论的基本合理标准.二者在前两种悖论中的合成结果几乎一致,但在处理0信任悖论的结果略有不同:1)本文方法分配了更多的信度给最有可能的疾病类型A,使结果更清晰,更有利于疾病诊断; 2)二者都分配了一定的信度给识别框架的全集,但本文方法对全集的信度m(Θ)更小,表明本文方法的不确定性更低.综上,本文方法更具有合理性. 例6.复杂战场环境中经常需要对多个传感器获得的决策判别信息进行融合.假设在某多源信息融合系统中,现有五类传感器对空中目标进行侦查识别,得到的识别结果可分为A,B,C这3种类型.其中,传感器1分别判定目标为类型A,B,C的置信度为0.3、0.2、0.05,判定类型为A或B的置信度为0.4,判定类型为A或C的置信度为0.05.传感器2分别判定目标为类型A,B,C的置信度为0.3、0.3、0.05,判定类型为A或B的置信度为0.3,判定类型为A或C的置信度为0.05.传感器3分别判定目标为类型A,B,C的置信度为0.05、0.1、0.6,判定类型为A或B的置信度为0.05,判定类型为A或C的置信度为0.2.传感器4分别判定目标为类型A,B,C的置信度为0.1、0.05、0.7,判定类型为A或B的置信度为0.05,判定类型为A或C的置信度为0.1.传感器5分别判定目标为类型A,B,C的置信度为0.2、0.2、0.2,判定类型为A或B的置信度为0.2,判定类型为A或C的置信度为0.2. 用证据的质量函数m1,…,m5分别表示以上5类传感器的识别结果.根据式(9),计算多个证据的BetPm值.根据算法1可以得到m1,…,m5中的主要焦元集合.根据算法2可将证据分为两个初始证据集ES1,ES2,其支持的主要焦元分别为ES1={A,B}和ES2={C}.分别计算m1,…,m5与这两个证据集的一致概率,以及证据与对应证据集之间的代价函数.并根据贝叶斯最小决策风险理论,可知:m1和m2与证据集ES1存在一致性,m3和m4与另一证据集ES2存在一致性,而m5与这两个证据集中立,划为边界证据. 对ES1,ES2证据集内部使用D-S规则进行合成.根据式(24)计算可得它们的权重分别为0.4,0.4.而边界证据的权重根据式(25)计算可得,最后使用修改后的D-S合成规则对它们进行合成.同样使用经典D-S规则和Yager法[32]等其他合成方法对例6中的证据进行合成,得到的结果如表4所示. 表4 不同方法的证据合成结果 在例6中,m1和m2主要支持识别类型为A和B,m3和m4主要支持识别类型为C,而m5对以上3种识别类型都予以支持.从每个焦元的平均可信度来说,C最高,A次之,B最低,因而其合成结果的合理标准应为:m(C)>m(A)>m(B).同时,复合焦元的信度之和越高,证据的不确定性越高.根据以上标准和表4可知,D-S合成规则和Murphy法不合理,Yager法和证据相关系数法虽满足该标准,但Yager法给焦元B分配了过少的可信度,且给复合焦元分配了相对较多的可信度,存在不合理.证据相关系数法和本文方法虽都符合以上合理标准,但结果存在以下差异:1)本文方法给单点集焦元分配的信度相对较高,更利于多源信息系统进行决策; 2)本文方法对复合焦元的可信度相对较低,说明本文方法不确定性更低,更具有参考意义.综上,本文方法更具优势. 证据融合方法是证据理论的重要研究内容.现有融合方法能有效处理冲突数据,但缺乏良好的可伸缩性,以至于在证据冲突较小时会引入不必要的计算量.因此,本文首先对证据之间的冲突关系进行了研究,建立了基于三支决策的证据关系模型.该模型利用证据的主要焦元和贝叶斯最小风险理论来判别证据之间的关系,并讨论了不同关系下对应的融合策略.其次,当多证据进行融合时,提出了基于三支决策的证据融合策略.该策略以证据集为单位来归并具有一致性的证据,避免了证据之间的逐次比较.通过应用三支决策证据关系模型来实现证据的三支划分.最后对这些被分配到不同证据集内部和边界上的证据进行修正与融合.结果表明,本文方法不仅能有效处理证据悖论,同时在充分利用证据信息的情况下能够减少计算量,得到合理的结果. 但本文方法仍存在一些不足:1)初始证据集的分布对融合结果可能会产生影响,下一步将改进计算初始证据集分布的算法; 2)计算证据权重时没有考虑到证据自身特性,在后续工作中可以结合证据的不确定性来修正权重.3.3 代价函数的设置
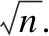
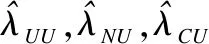
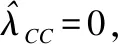
3.4 证据关系对融合策略的影响
4 基于三支决策的证据融合策略
4.1 初始证据集上的焦元分布
4.2 证据的三支划分
4.3 证据的修正与融合
4.4 计算量分析
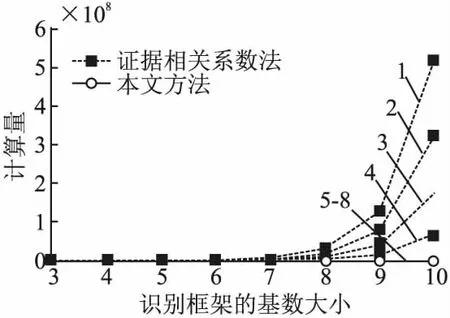
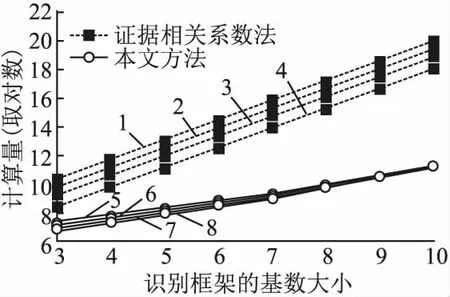
5 算例分析
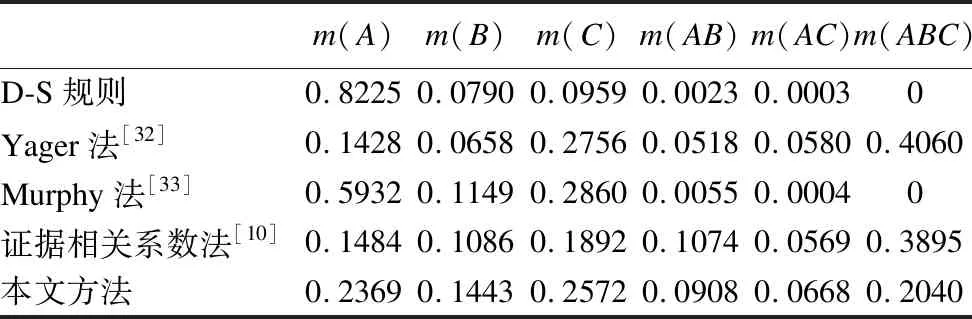
5.1 证据悖论分析

5.2 多证据合成分析
6 总 结

