含多球铰间隙并联机构动力学建模与响应分析

陈修龙, 张昊

(山东科技大学 机械电子工程学院,山东 青岛 266590)

并联机器人具有结构紧凑、可承受载荷大、自身惯性小等优点[1-3],并联机构是并联机器人的骨架。球铰连接能使机构实现3个方向的转动,转动范围大,灵活性好,在并联机构中应用广泛[4],受到加工精度、装配需要等因素影响,球铰之间必然会产生间隙,间隙的产生会使并联机构产生噪声和振动,降低运动精度,缩短机构的使用寿命[5]。因此,为了分析机构的动力学响应,建立含球铰间隙的并联机构动力学模型,对于预测机构在实际使用中的动力学行为具有重要意义。

目前,在对机构的运动副间隙研究领域,大多数国内外学者的研究针对的是含间隙的平面机构,对含间隙空间并联机构的研究较少。Song等[6]提出了一种含多个转动副间隙的平面多体动力学建模方法,并用ADAMS软件仿真验证其正确性;Chen等[7]分析了含转动副间隙的曲柄滑块机构的动态特性;Ma等[8]建立了含多个转动副间隙的平面多体动力学模型,研究多间隙对机构动力学响应的影响;郑恩来等[9]以含转动副润滑间隙的平面柔性多连杆系统为例,研究机构的动力学响应;Muvengei等[10]分析了考虑多个转动副间隙机构的动态响应特性;Wang等[11]提出了一种含间隙多体系统动力学模型,分析了间隙位置、间隙数量对机构动态响应的影响;Zheng等[12]研究了转动副间隙和柔性构件如何影响多连杆压力机的动力学特性;赵宽等[13]基于Lagrange方程,以含转动副间隙曲柄滑块机构为研究对象,分析了该机构的动力学响应特性;Wang等[14]研究了含单个球面副和柔性构件的空间4-SPS/PS机构的动力学响应;陈修龙等[15]以4-UPS-RPU空间并联机构为研究对象,建立其含单个间隙的刚体动力学模型,研究间隙值大小对其动态特性的影响。

本文选用空间并联机构三维模型3-SPS-S并联机构为研究对象,为了推导出准确的球铰间隙处的碰撞力模型,采用基于Flores法向接触力模型和改进的Coulomb摩擦力模型的方法,并利用Lagrange乘子法建立含多个球铰间隙的并联机构动力学模型,将求解程序写入Matlab软件,从而计算得到动力学响应结果,并用ADAMS软件进行虚拟样机仿真验证。

1 机构特征及球铰间隙模型

3-SPS-S空间并联机构的三维模型如图1所示。该机构主要由定平台、动平台、3条SPS结构的驱动支链和1条S结构的约束支链组成,驱动支链由伸缩杆和摆动杆构成,其中S表示球铰,P表示移动副。

图1 3-SPS-S空间并联机构三维模型Fig.1 Three dimensional drawing of 3-SPS-S spatial parallel mechanism

通过改进的Kutzbach-Grubler公式计算其自由度[16],得出该机构有3个自由度,给3个驱动支链添加驱动后,能使动平台有确定的运动,约束支链的存在使得动平台沿3个方向的移动被限制,所以动平台能够实现3个方向的转动。此机构可作为指向机构和调姿机构的底座,实现对动平台姿态的精准控制。

图2所示为球铰的间隙模型,g、h分别表示与球窝和球头相连的2个构件,与构件g、h固连的2个局部坐标系可分别表示为Og-xgygzg和Oh-xhyhzh,局部坐标系Og-xgygzg和Oh-xhyhzh的原点在定坐标系OA-XAYAZA下的位置矢量可分别表示为rg和rh。Pg表示球窝中心,rPg为球窝中心在固定坐标系下的位置矢量表示;Ph表示球头中心,rPh为球头中心在固定坐标系下的位置矢量表示。Qg和Qh分别表示球窝和球头的碰撞点,n表示接触面的法向单位向量,t表示接触面的切向单位向量。

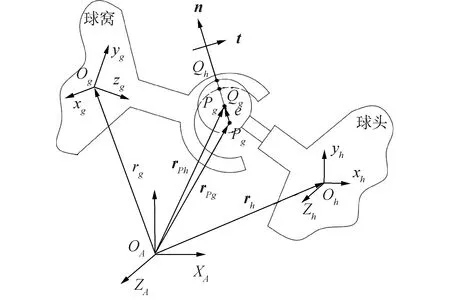
图2 球铰间隙模型Fig.2 Clearance model of spherical hinge

球头相对于球窝的偏心向量为[17]:

e=rPh-rPg

(1)

偏心矢量的单位矢量为:

n=e/e

(2)

其中,偏心幅值e为:

(3)

穿透深度为:

δ=e-c

(4)

式中:c表示球头与球窝之间的间隙值,c=Rg-Rh;Rg和Rh分别表示球窝与球头的半径。球头与球窝之间的碰撞状态可由穿透深度判断,当δ>0时,球头与球窝之间为碰撞状态,当δ≤0时,球头与球窝之间为刚好接触或者为分离的状态。在数值计算过程中,球头与球窝间的碰撞状态为:

δ(q,t)·δ(q,t+Δt)≤0

(5)

当球头与球窝之间的状态满足式(5)且满足δ(q,t)≤0时,在t+Δt时刻发生了碰撞。

球窝、球头的碰撞点在定系下的位置矢量分别用rQg和rQh为:

(6)

式(6)两边对时间t求一阶导数,得到球窝、球头的碰撞点在定系下的速度矢量为:

(7)

(8)

由式(7)可得在碰撞点处,球头相对于球窝的速度矢量,将此速度在接触面上投影,可得到球头相对于球窝的法向速度和切向速度,即:

(9)

2 球铰间隙接触力模型及并联机构动力学模型的建立

2.1 法向接触力模型的建立

Hertz理论中两物体的纯弹性接触碰撞,没有考虑阻尼造成的能量损失[18],L-N接触力模型[19]适用于恢复系数近似为1的材料,而Flores接触力模型[20]对恢复系数无特殊要求,因此,本文采用Flores接触力模型建立球头与球窝的接触力模型,表达式为:

(10)

式(10)中的刚度系数K为:

(11)

其中,球窝和球头的碰撞深度为:

(12)

式中:vg和vh分别表示球窝和球头的泊松比;Eg和Eh分别为球窝和球头的弹性模量。

2.2 切向接触力模型建立

利用改进的Coulomb摩擦力模型[21]描述球头与球窝发生碰撞时的切向接触力,此模型引入系数cd,避免了切向速度在0附近方向发生改变而造成积分求解不稳定的情况:

(13)

式中:μd为滑动摩擦系数;cd为动态修正系数,取值依据为:

(14)

式中的v1和v2为给定的速度极限值。

通过对法向接触力和切向接触力求解,得到球头对球窝的接触力为:

Fg=Fn·n+Ft·t

(15)

球窝作用于球头上的力与其方向相反:

Fh=-Fg

(16)

接触力对构件g和h的质心处产生的力矩为:

(17)

2.3 坐标系的建立及转换

图3为3-SPS-S空间并联机构的结构简图,该机构由定平台、动平台、3条呈120°均布的SPS驱动支链和中间1条约束支链组成,每个驱动支链中包含一个摆动杆和一个伸缩杆。定平台A,摆动杆用1、2、3表示,伸缩杆用4、5、6表示,动平台用7表示。通过球铰Si(i=1,2,3)连接定平台与摆动杆,通过球铰Sj(j=4,5,6)连接动平台与伸缩杆,通过移动副Pi(i=1,2,3)连接摆动杆与伸缩杆,约束支链下方与定平台直接固连,上方通过球铰S7与动平台连接。

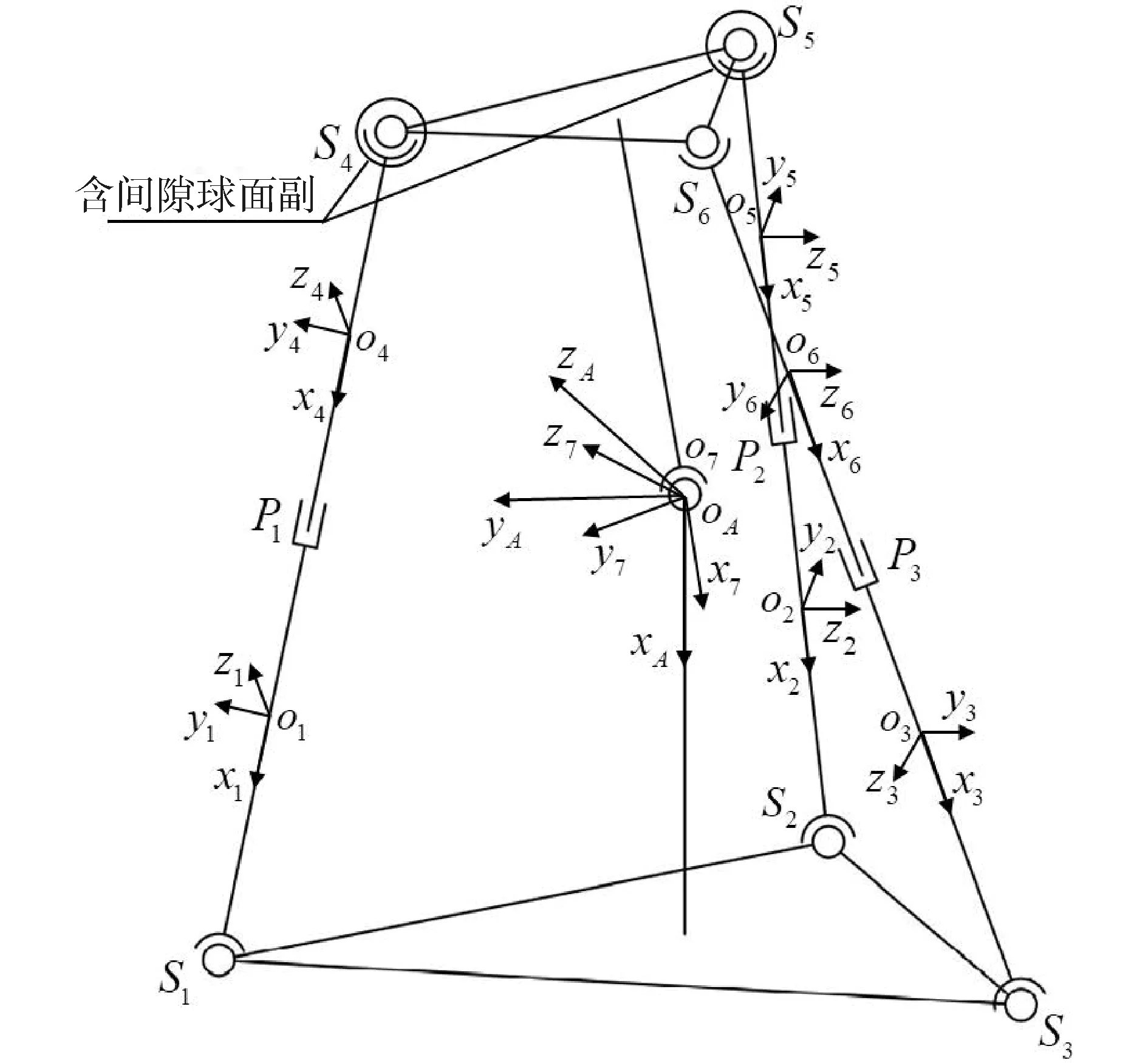
图3 3-SPS-S空间并联机构简图Fig.3 3-SPS-S spatial parallel mechanism

定平台的质量mA,在定平台的质心处建立固定坐标系OA-XAYAZA,XA轴方向沿着定平台竖直方向向下,YA轴方向沿着固定坐标系原点OA指向球铰S1的方向,ZA轴方向通过右手定则确定,在以OA为圆心,rA为半径的圆上,布置有球铰Si(i=1,2,3),每2个球铰之间呈2π/3均布。

动平台的质量m7,在动平台的质心处建立局部坐标系O7-X7Y7Z7,坐标系原点与球铰S7的中心重合,X7轴方向沿着动平台竖直方向向下,Y7轴方向沿着局部坐标系原点O7指向球铰S4的方向,Z7轴方向通过右手定则确定,在以O7为圆心,rB为半径的圆上,布置有球铰Si(i=4,5,6),每2个球铰之间呈2π/3均布。

摆动杆的质量mi(i=1,2,3),长度li(i=1,2,3),将杆长的中心点近似地看做质心,建立局部坐标系Oi-XiYiZi(i=1,2,3),伸缩杆的质量用mj(j=4,5,6)表示,长度用lj(j=4,5,6)表示,同理,建立局部坐标系Oj-XjYjZj(j=4,5,6)。

通过欧拉角转换,将固定坐标系的姿态转换为局部坐标系的姿态,转换方式为X-Y-Z,即:先绕X轴旋转α角,再绕Z′轴旋转β角,最后绕Y″轴旋转γ角。转换矩阵为:

R(α,β,γ)=R(X,α)R(Z,β)R(Y,γ)

(18)

2.4 动力学模型的建立

3-SPS-S空间并联机构有7个活动构件,每个活动构件有6个广义坐标,包括位置和姿态。建立7个活动构件的广义坐标为:

(19)

ΦSi(i=1,2,3,6,7)和ΦPi(i=1,2,3)分别表示球铰和移动副的约束方程,由于球铰S4和球铰S5存在间隙,使得球头和球窝的中心不再重合,在球头和球窝碰撞过程中会产生接触力,因此,这两处的约束方程被接触力取代。得到含多个球铰间隙的3-SPS-S空间并联机构的约束方程为:

Φ(q)*=(ΦS1;ΦS2;ΦS3;ΦS6;ΦS7;

ΦP1;ΦP2;ΦP3;ΦQ)=033×1

(20)

对式(23)关于时间求一次导数,得到速度约束方程:

(21)

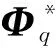
(22)

建立含多个球铰间隙的3-SPS-S空间并联机构的动力学方程为:

(23)

式中:λ为拉格朗日乘子;Q*为构件的广义力矩阵。

结合式(22)和式(23),得出微分代数形式的动力学方程为:

(24)

(25)

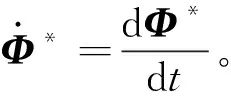
将求解参数输入Matlab软件,通过四阶Runge-Kutta算法计算,利用Ode45求解器得到结果,流程如图4所示。

图4 含间隙动力学求解流程Fig.4 Flow chart of dynamic solution with clearance

3 含球铰间隙的3-SPS-S空间并联机构动力学响应分析

3.1 并联机构的参数设定

3-SPS-S空间并联机构的各个构件的参数由表1列出,用Matlab软件进行动力学求解时,参数设定由表2列出。

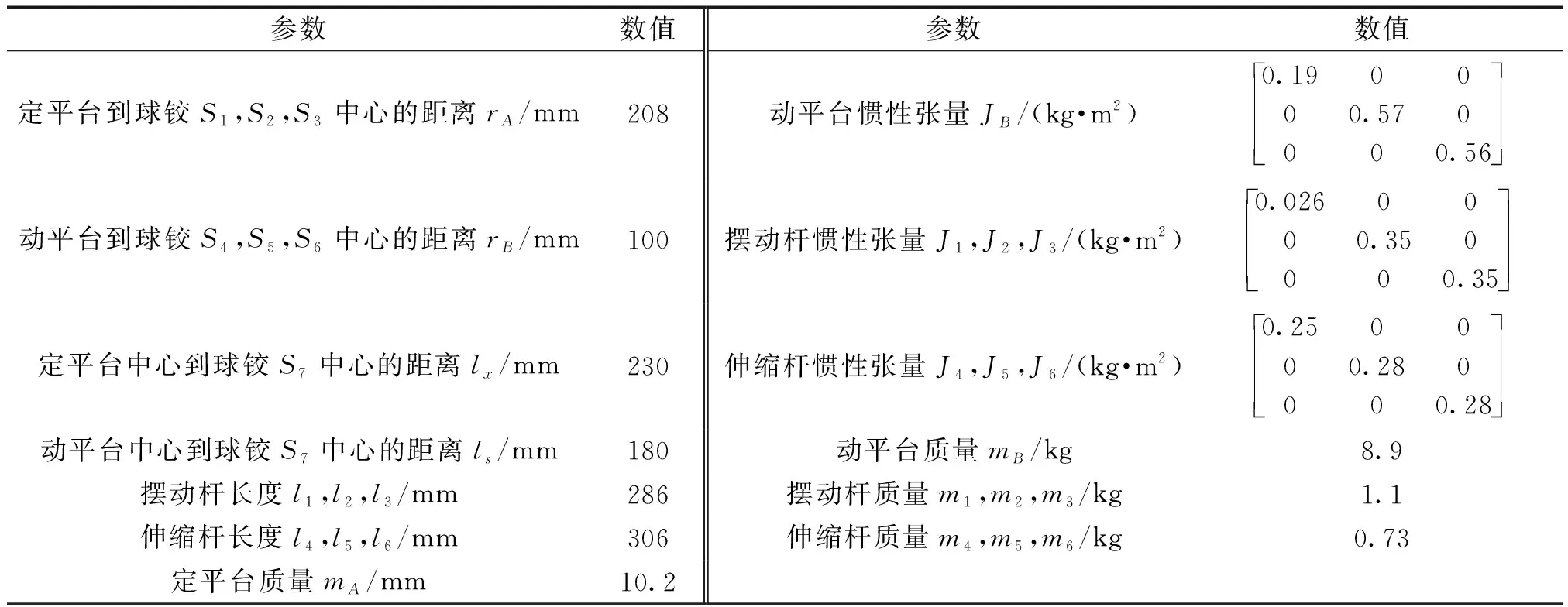
表1 3-SPS-S空间并联机构的各构件参数Table 1 Parameters of 3-SPS-S spatial parallel mechanism

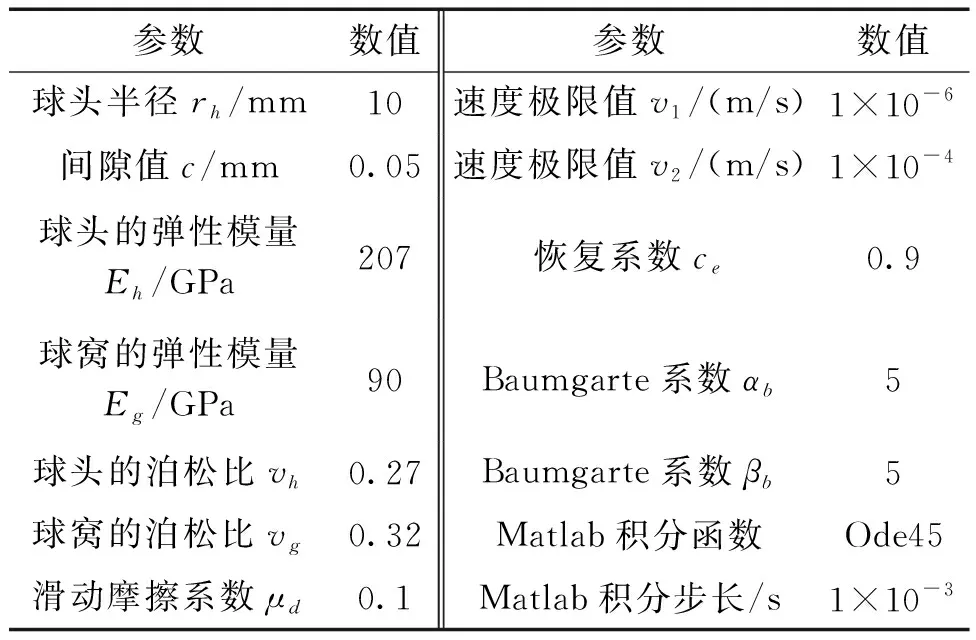
表2 3-SPS-S空间并联机构动力学求解参数Table 2 3-SPS-S spatial parallel mechanism dynamic solution parameters

3-SPS-S空间并联机构的动平台运动特征为绕x轴、y轴、z轴方向的转动,采用运动学反解方法,先给定动平台运动轨迹为:

(26)

利用Matlab软件进行数值求解得到机构的动力学响应图像,分析单个球铰间隙、多个间隙球铰间隙对机构动力学响应的不同影响。

3.2 含间隙机构动力学响应的理论与仿真对比

3.2.1 考虑5号球铰间隙对机构动力学响应的影响

5号球铰在含0.05 mm间隙情况下的动力学响应如图5～9所示,在角位移、角速度、角加速度方面,将Matlab理论值与ADAMS仿真值进行对比,验证了结果的正确性。

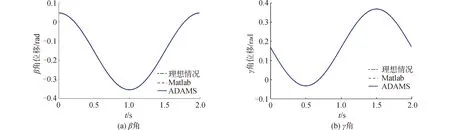
图5 单间隙下动平台角位移对比Fig.5 Single clearance moving platform displacement comparison

图5(a)为动平台绕β角转动的角位移,从图中可以看出,动平台的转动角度范围-0.354～0.046 rad,且含间隙情况与无间隙情况之间无明显偏差;图5(b)为动平台绕γ角转动的角位移,从图中可以看出,动平台的转动角度范围在-0.032～0.369 rad,且含间隙情况与无间隙情况之间无明显偏差。

图6分别为动平台绕β角和绕γ角转动的角速度,两者的角速度范围分别为-0.628 6～0.628 9 rad/s和-0.628 3～0.629 rad/s,两者在开始时刻和波峰波谷处出现明显抖动,说明间隙对动平台的角速度产生了一定的影响,在理论值方面,绕β角转动的角速度最大波动量为0.036～0.19 rad/s,绕γ角转动的角速度最大波动量为-0.045 5 rad/s。

图6 单间隙下动平台角速度对比Fig.6 Single clearance moving platform velocity comparison

图7分别为动平台绕β角和γ角转动的角加速度,从图中可以看出,在机构开始运动的瞬间,动平台的角加速度出现剧烈波动。分析图7可知,动平台绕β角的角加速度理论值峰值为29.67 rad/s2,仿真峰值为20.96 rad/s2,随后慢慢趋于稳定,在0.619～0.738 s时间内,仿真曲线发生轻微波动。分析图10可知,动平台绕γ角的角加速度理论值峰值为68.7 rad/s2,仿真峰值为64.08 rad/s2,随后慢慢趋于稳定,在0.614～0.716 s时间内,仿真曲线发生轻微波动。

图7 单间隙下动平台角加速度对比Fig.7 Single clearance moving platform acceleration comparison

图8为球头与球窝之间的碰撞力,在初始时刻,机构由静止到突然发生碰撞,会使碰撞力达到峰值66.56 N,随后慢慢趋于稳定,在0.901 3～7.256 N波动。

图8 球头与球窝的碰撞力Fig.8 Impact force between ball joint and ball socket

图9为球头的中心轨迹图,在初始时刻,球头中心位于中间位置,随着机构运行,球头中心开始偏移并与球窝发生碰撞,最后相对于球窝发生很小范围摆动。

图9 球头中心轨迹Fig.9 Ball joint center track

3.2.2 考虑4号球铰和5号球铰间隙对机构动力学响应的影响

为了观测间隙球铰的数量对机构动力学响应的影响,将4号球铰和5号球铰添加0.05 mm间隙,利用Matlab软件绘制动平台响应图像,将理论结果和仿真结果进行对比从而验证结果的正确性。

图10为多间隙下动平台绕β角和绕γ角转动的角位移图像,和单间隙的情况相比,偏差明显增加,但总体趋势保持稳定。

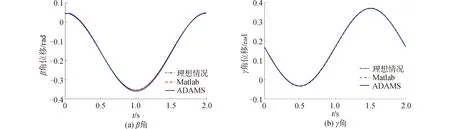
图10 多间隙下动平台角位移对比Fig.10 Multi clearance moving platform displacement comparison

图11分别为多间隙下动平台绕β角和绕γ角转动的角速度,由图像可以看出,在机构由静止到运动的瞬间以及波峰波谷位置会出现较为明显的偏差,说明多间隙对机构角速度的影响较大,其中,β方向的最大偏差为0.171 5 rad/s,γ方向的最大偏差为0.121 2 rad/s。

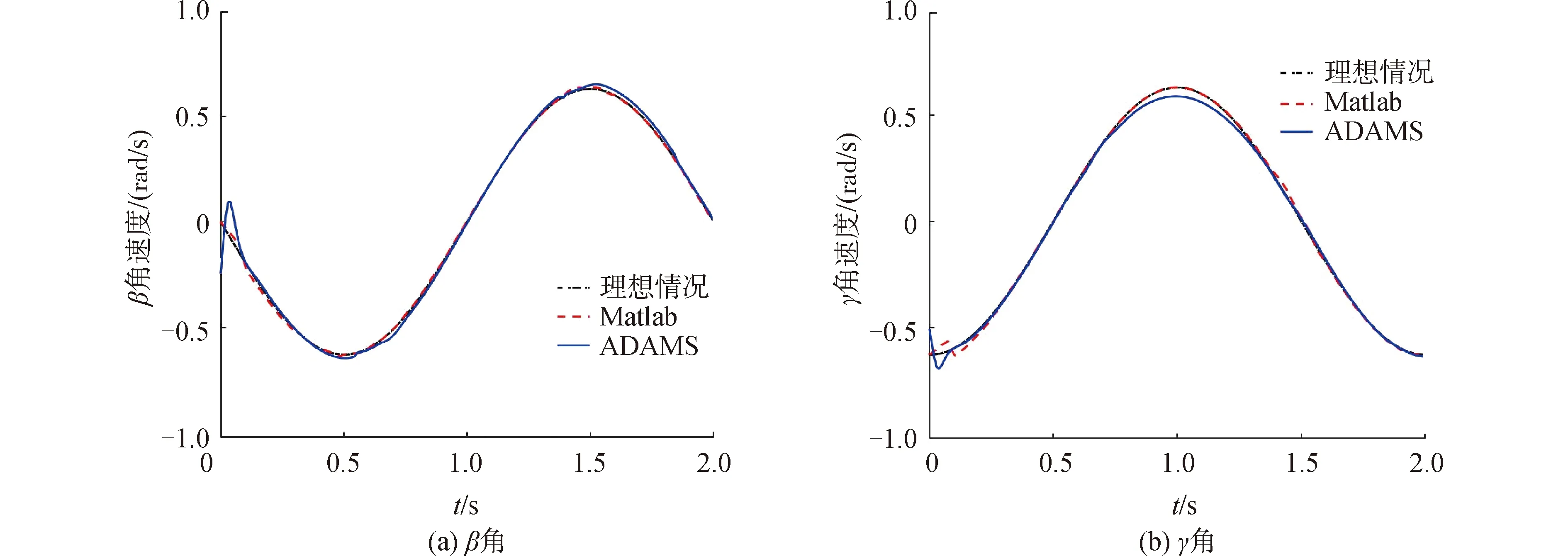
图11 多间隙下动平台角速度对比Fig.11 Multi clearance moving platform velocity comparison

图12分别为多间隙下动平台绕β角和绕γ角转动的角加速度,通过与单间隙对比可以发现,由于间隙之间的耦合作用,初始时刻加速度峰值明显下降,但随后运行过程中的波动点数量明显增加,机构稳定性降低。

图12 多间隙下动平台角加速度对比Fig.12 Multi clearance moving platform velocity comparison

在理论值方面,β方向的峰值为-4.586 rad/s2,γ方向的峰值为-3.167 rad/s2,在仿真值方面,β方向的峰值为-7.412 rad/s2,γ方向的峰值为-3.04 rad/s2。可以看出理论值与仿真值之间有一定的差异,且后续的几个波动点的值也不是完全重合,但都在合理范围之内,图像总体趋势不变,说明结果正确。

4 结论

1)球铰间隙对动平台的角位移和角速度的影响较小,对角加速度和碰撞力的影响较大。

2)含间隙球铰数量越多,机构的稳定性越差。本研究对并联机构中球铰的加工精度、装配误差的控制等方面具有重要的理论指导意义。