深挖试题背景 把握命题方向*
——以一道解析几何试题为例
广东省惠州仲恺中学 (516229) 陈伟流
纵观近几年的高考解析几何试题,绝大部分都以丰富的背景和内涵,如“手电筒模型”、“圆锥曲线的极点极线”、“阿基米德三角形”、“彭赛列圆”等知识理论,而成为广大师生深耕不倦的“香饽饽”.高考以试题为考核载体,重点考查了学生运算求解,逻辑思维,空间想象等关键能力,渗透了对数学核心学科核心素养的隐性测评.因此,身为教育的先行者,教师在解题教学实践,要通过深挖试题背景,还原命题本质,探讨试题所反映的一般性规律,这样才能精准把握命题方向,在教学实践中扮演好指明灯的重要角色,从而培养好学生的数学核心素养.本文通过对2023届惠州三调解析几何试题的背景溯源,整体构建,纵向深化,横向迁移等探索之旅,以此为基础提出在解析几何试题命制的个人尝试,期待能与读者在思维上碰撞出更多的火花.
1 试题再现
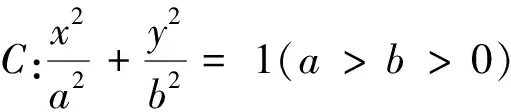
⑴求椭圆C的方程;
⑵如图1,点P,Q分别在C和直线x=4上,OQ∥AP,M为AP的中点,若T是直线OM与直线QF的交点.是否存在确定的一个曲线,使得T始终在该曲线上?若存在,求出该曲线的方程;若不存在,请说明理由.

图1


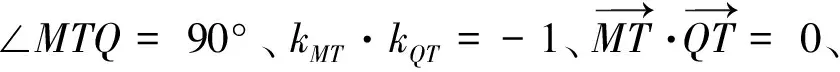
2 背景溯源
因点F为椭圆的右焦点,直线x=4为其右准线,若将椭圆方程及对应条件的参数一般化处理,有
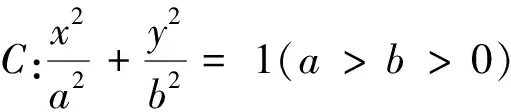
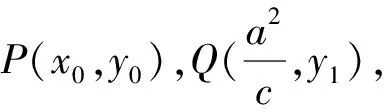
注意到右焦点及右准线是椭圆的一对特殊的极点和极线,若将其进一步一般化,有
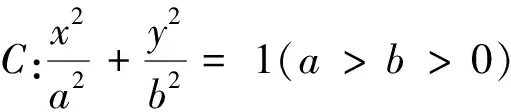
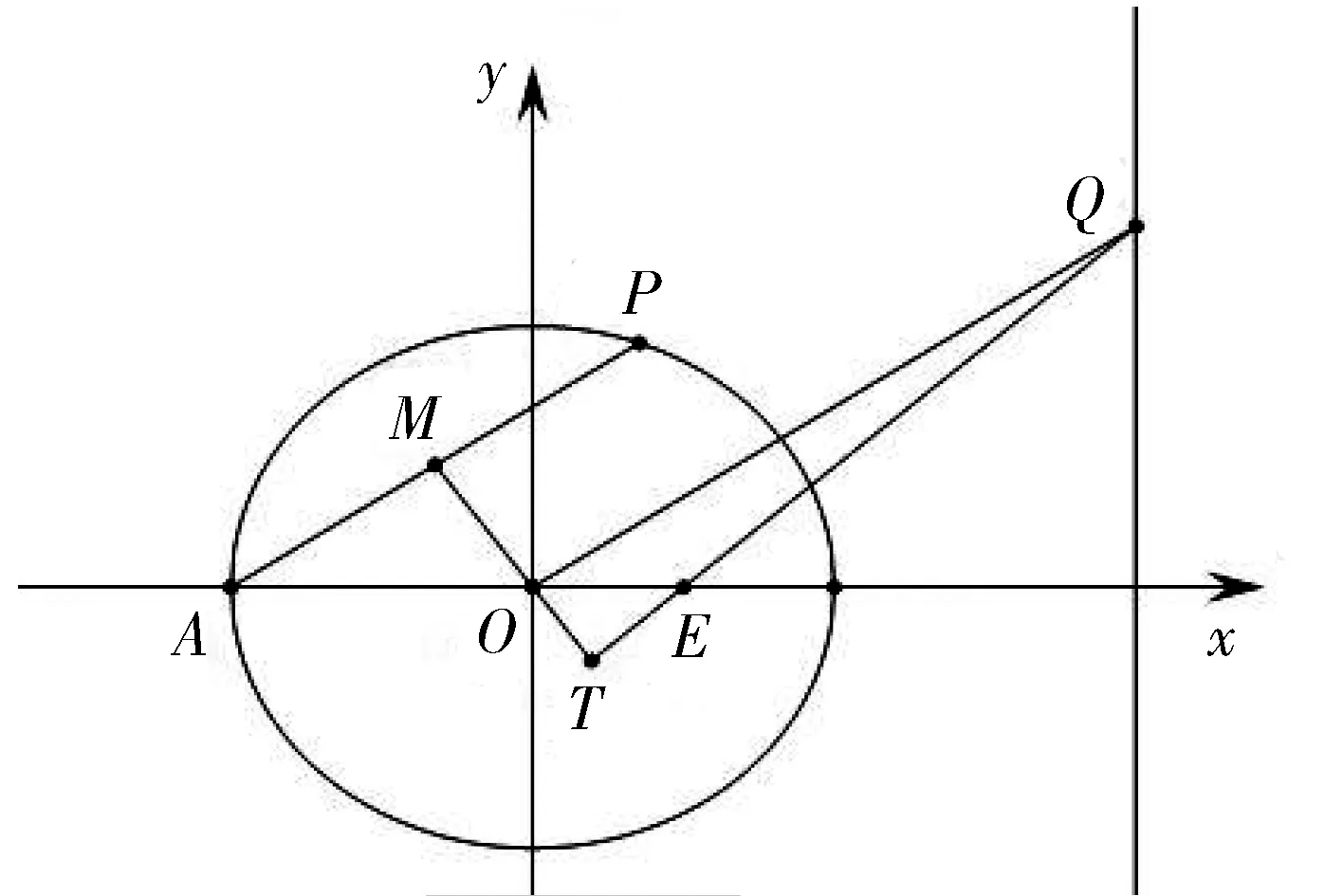
图2


3 整体构建

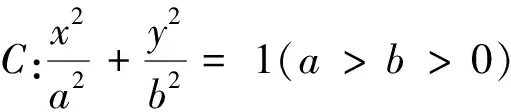
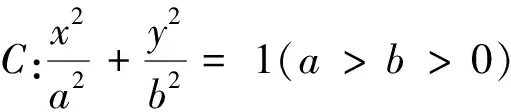
4 纵向深化
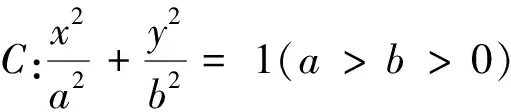

图3
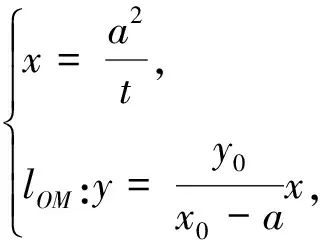


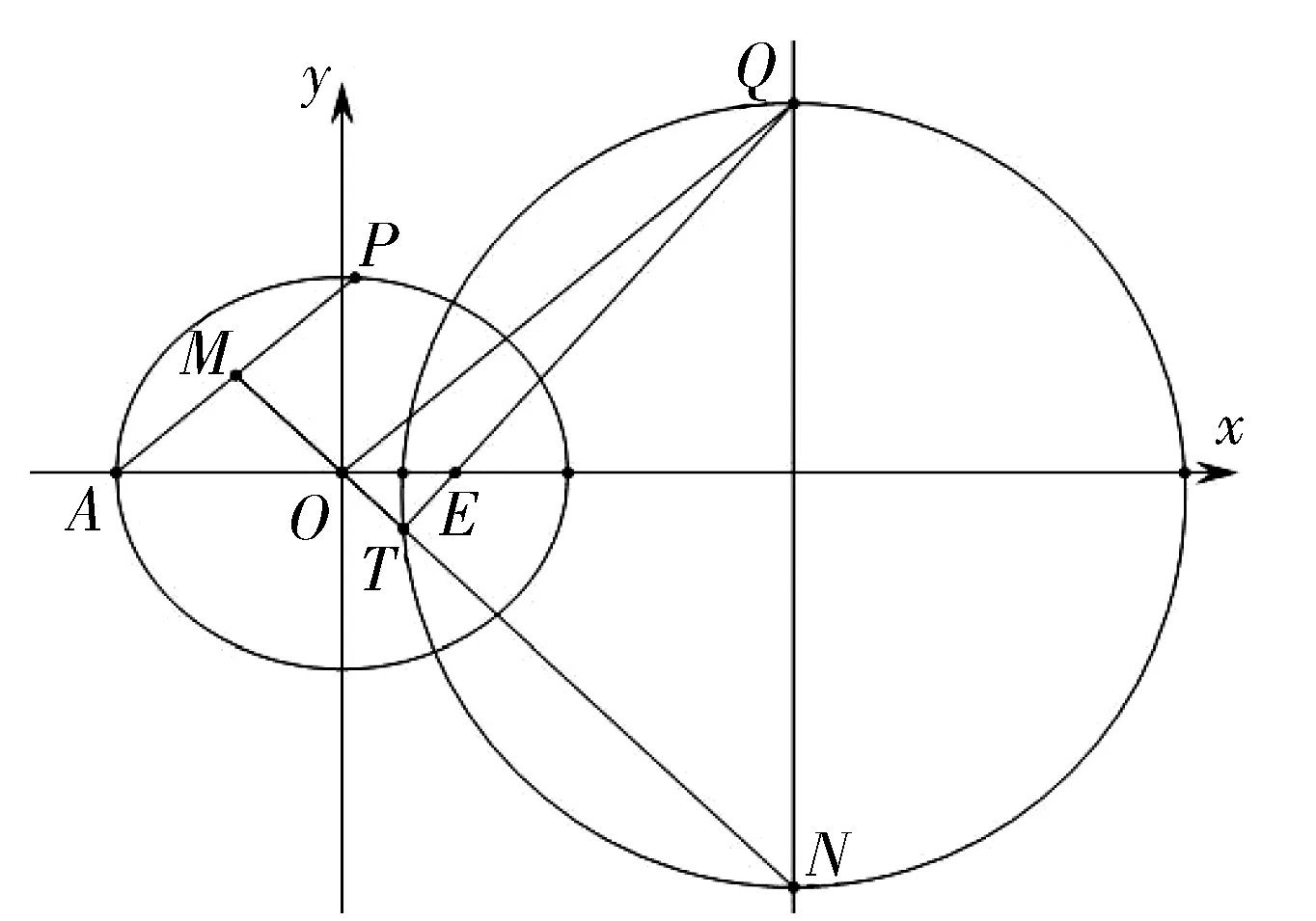
图4

5 横向类比
基于圆锥曲线知识体系的统一性,将探究背景置换为双曲线,经笔者探究,有





6 命题初探
高考中的解析几何试题往往依托于圆锥曲线体系中的某个经典知识理论,再取某些特殊几何信息点为条件支撑,历经演绎推理的论证过程,从而产生了高度概括性的一般化结论.通过试题关键信息点的合理解构与有机重构,再类比迁移到其他圆锥曲线,结合学情及考点方向,便可创作出一系列背景深厚,结论优美,耐人寻味的高考母题.经历前文对试题进行背景溯源,整体构建,纵向深化及横向类比的推理探究过程,笔者以定值,定点等作为命题方向进行尝试,以期待与读者有更深入的交流.

⑴求椭圆C的方程;⑵点P,Q分别在C和直线x=4上,OQ∥AP,M为AP的中点,若T是直线OM与直线QF的交点,是否存在定点E,使得点T在运动过程中,始终保持线段ET的长度恒为定值?若存在,求出定点E的坐标;若不存在,请说明理由.

⑴求椭圆C的方程;⑵点P,Q分别在C和直线x=4上,OQ∥AP,M为AP的中点,设直线OM交直线x=4相交于N.当P在椭圆上运动时,试证明:以线段QN为直径的圆恒过定点.

