在解题教学中发展和完善学生的CPFS结构

江苏省苏州新区第一中学 (215011) 周恩超

分析学生解题过程中的错误根源,能使我们认识到学生认知结构的残缺,从而使教学有的放矢.帮助学生完善CPFS结构,更有利于学生的问题解决,对此我在教学实践中深有体会.在一次数学测验中,曾对一道问题的错解进行了如下统计和访谈:

一、对一道题目的错解分析

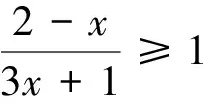
(1)若B⊆A∩B,求实数a的取值范围;

(2)若A∩B≠φ,求实数a的取值范围．

调查对象：内地新疆高中预科(1)班,全班45人,数学基础良好,中考数学成绩均分118分(满分130分).其中,女生27人、男生18人.

错解统计：

(1)第(1)问全班有3人作对,其他42人出现了错误,其错误情况如下:

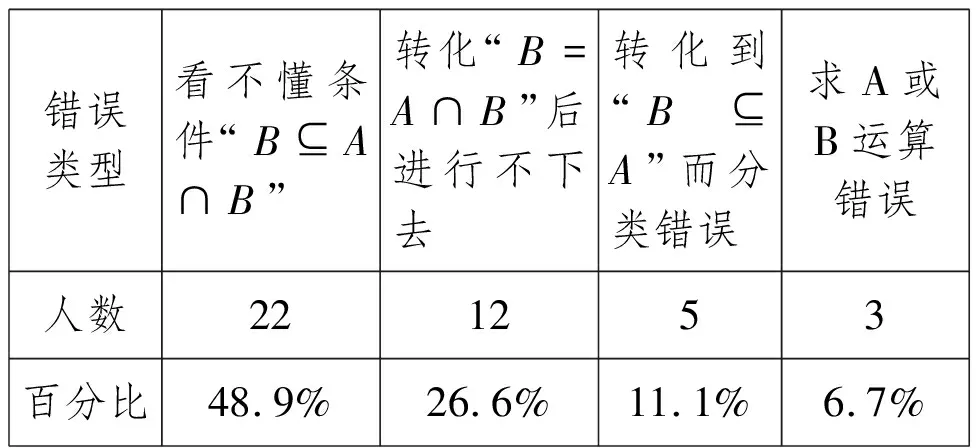
错误类型看不懂条件“B⊆A∩B”转化“B=A∩B”后进行不下去转化到“B⊆A”而分类错误求A或B运算错误人数221253百分比48.9%26.6%11.1%6.7%

(2)第(2)问中,全班没有一个同学取得满分,有5位同学没做,其余40位同学均采用分别求出集合A,B,然后再考虑使用条件A∩B≠φ,其中有18位同学直接运用条件A∩B≠φ,即思考如何让集合A,B交集非空;另外22位同学将问题转化为求“A∩B=φ”时的情况,而在分类讨论中出现了逻辑或运算错误.令人遗憾的是,以下两种解法在试卷上均没有出现:

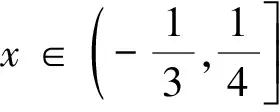
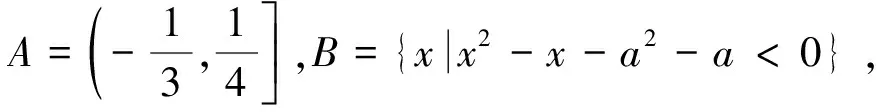
访谈分析：为什么对这道题目的解答错误率很高,根据该题目两问中不同的错误类型,分别选出部分同学进行了访谈:

师:如何理解条件“B⊆A∩B”?

生:不知道这个条件是什么意思,换言之,不知如何满足这个条件.

生:我只知道“A∩B⊆B”或者“A∩B⊆A”一定是成立的,而该题目中的条件“B⊆A∩B”让人不可理解,是不是题目错了.

师:如何理解“B⊆A∩B”与“A∩B⊆B”同时成立?

生:不能理解,我认为这是矛盾的.

生:可以理解,条件“B⊆A∩B”是人为给出的;而“A∩B⊆B”是一个基本事实.这两个条件如果不矛盾的话,必须要有“A∩B=B”.

师:理解得很好,可如何理解“A∩B=B”?

生:我觉得所得到的这个条件也是矛盾的,“A∩B”是集合“B”的一部分,那么,“部分”怎么可能与“整体”相等呢?

生:我觉得可以理解,如果“A∩B=B”,则意味着“B⊆A”.

师:如何理解“B⊆A”呢?

生:“B⊆A”就是说,集合B中的每一个元素都在集合A,但集合A中的元素一不定在集合B中.

师:回答很好,但如果集合B中没有元素,可以说“B⊆A”吗?你能用文恩图来说明“B⊆A”的几种情况吗?

在老师的提醒下,学生恍然大悟,意识到空集是任何集合的子集.

生:“B⊆A”应包括三种情况:B=φ;B⊄A;B=A.

师:怎么理解xo∈{x|x2-x-a2-a<0}?

生:xo∈{x|x2-x-a2-a<0},即xo满足条件x2-x-a2-a<0,从而不等式xo2-xo-a2-a<0成立.

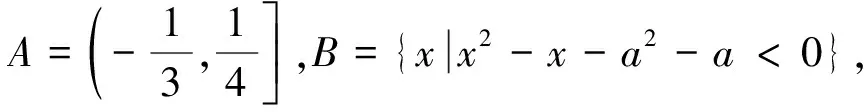
生:如果老师不提出这个问题的话,根本不会去想到将条件“A∩B=φ,A∩B≠φ”向恒成立或存在性问题方面去转化.在老师的提醒下,好像可以那样去理解了.

二、完善学生CPFS结构对问题解决具有重要意义

有了跟同学们的以上交流,不难理解学生思维受阻原因了,他们找不到解决问题的突破口,关键是学生的“CPFS”结构残缺、不完善导致.所谓“CPFS”结构即概念域、概念系、命题域、命题系形成的结构(概念域(concept field)、概念系(concept system),以及命题域(proposition field)、命题系(proposition system).

在数学问题解决的过程中,如何将问题条件或结论用数学语言去作等价描述,即对问题如何进行“有意义的等价表征”,这是解题思路获得的前提和开端;其次要积极寻找当前问题的“迁移源”,进行模式识别、概括、类比的合理借鉴,而不是盲目地“试误”;再者,在解决问题的执行过程中,同样需要解题者自我监控,及时反思、调整.以上都需要解题者具备相关问题的概念域(系)和命题域(系),而个体形成了良好的CPFS结构,就是在长时记忆中贮存了与所要解决的问题相关的数学知识信息,知识间彼此相连,形成个性的、稳固的知识网络,新问题的解决的实质就是搜寻、提取、激活相关知识结点的过程.CPFS结构是数学所特有的认知结构,它不但包括数学的概念、公式、定理、公理等“硬件”,而且包括数学思想方法、数学观念等“软件”.其知识命题之间除了上、下位关系外,还包括“等价”这种同位关系,因而,知识结点的激活将更容易、更全面,解决问题的渠道更加畅通.试想,如果我们能在日常教学中,根据学生们的数学解题体验,帮助学生逐步建立、完善“CPFS结构”,那么对学生的解题该有多大帮助.

三、发展和完善学生CPFS结构的教学策略

1、在概念、命题教学中,加强数学理解形成网络体系

在概念、命题教学中,一定要重视知识产生、发展的过程,深刻认识数学对象的背景、产生途径和规则的逻辑依据,把握数学对象的本质,帮助学生建立关于以上观念的内部网络.只有学生了解了一个概念(或命题)与其他概念(或命题)的相互关系以及它们在优化后的认知结构中的位置,学生才能真正地视为己有,才能灵活地迁移应用.要引导学生学会从系统的观点整理概念和命题的方法,把有关概念和命题串成锁链、编成网络、配以图示、纵横联系,使学生主动获得一个个有序的概念组和命题组块,能从整体中看部分,从部分中看整体.

2、在解题教学中,通过反思、提炼数学体验完善认知结构

问题是数学的心脏,寻找和发现数学问题,是获得数学发现和进行数学思维的基本方法之一,同时,也是完善和发展个体“CPFS”结构的必经途径.在解题教学中,要重视学生的数学体验,引导学生在数学实践中反思、整理、归纳、提升,模式识别分类后进行有意义储存,达成“长时记忆效果”.在具体教学中,多采取“问题链”、“抛锚式”的教学策略,适当进行变式教学,一题多解、并多解选优.重视解题后的回顾与反思,培养学生“研究意识”,及时积累加工后的“雕虫小技”,让思考、积累成为一种习惯.在“理论、实践、再理论、再实践”的螺旋交互过程中,内化、补充、优化、完善已有的认知结构.例如在集合教学中通过以下题组训练:

(1)已知集合A=[1,2],B={x|x2-x-a≤0},若A⊆B,求实数a的取值范围?

(2)已知集合A=[1,2],B={x|x2-x-a≤0},若A∩B=φ,求实数a的取值范围?

(3)已知集合A=[1,2],B={x|x2-x-a≤0},若A∩B≠φ,求实数a的取值范围?

让学生深刻理解集合语言“A⊆B、A∩B=φ、A∩B≠φ”的等价表征,将问题转化为“恒成立问题或存在性问题”解决,由此展开并结合学生原有的解题实践,帮助学生逐步建立完善以下认知结构:

图1

3、重视元认知教学策略,提高学生自我监控能力

数学解题的认知结构是由解题知识结构、思维

结构和解题的元认知结构所组成.因此加强学生数学元认知能力的培养,有利于训练学生解决问题的“自醒意识”,避免走弯路或少走弯路,并能做好及时调节.一旦这种“自我监控能力”得到提高,就会从根本上改善学生的学习方式,学生个体“CPFS结构”的生成建构,便会由点到线、由线到面.同时,也会随着学生数学认识的提高和对数学实践的反思,对已有的“CPFS结构”进行动态调整、完善.所以,帮助学生提高元认知知识,丰富学生的元认知体验,指导学生调节与监控自己的学习过程,是教师日常教学中不应忽视的重要任务.

发展和完善学生的“CPFS结构”对学生的数学学习意义重大,对老师的教学提出更高的要求和挑战.对此,我们应不懈努力.