基于有效风速估计的永磁直驱风力发电系统鲁棒控制研究

李 雷，杨建林，冯振江，邹范岗，鲍 强，李源开，赵晋斌

（1.国家电投集团山东能源发展有限公司鲁西分公司，山东济南 250014；2.上海能源科技发展有限公司，上海 200233；3.上海电力大学，上海 200090）

0 引言

随着化石和储能资源的日益枯竭，由于风能自身的清洁性以及高效能源变换技术的发展，风能成为有前途的能源之一[1-3]。通常，风力发电系统通过检测当前风速，控制风力发电的机械转矩和转速，使风力发电机工作点达到风能利用率曲线最大值点附近，实现最大功率跟踪控制[4-7]。然而，由于风剪切、塔影效应、湍流、传感器故障等多方面的影响，导致风速传感器感知的风速值可能偏离施加在风力机叶片上的有效风速，进而导致风力发电机对风能的利用率降低[8-11]。

为了提高风力发电效率，国内外学者提出了多种风力发电机的最大功率跟踪控制策略，主要包括最佳叶尖速比法、扰动观察法、观测器法等[12-16]。其中，滑模观测器可修正风力发电系统中传感器感知的状态量，提升风力发电机整体的控制性能和鲁棒性，因此备受青睐。文献[17]针对永磁直驱同步风力发电机（Permanent Magnet Synchronous Generator，PMSG），设计了自适应滑模控制器算法，通过估计转速和转矩，实现了在多种风速下永磁直驱风机并网系统控制性能的提升。为了减小观测器输出的抖动，文献[18]提出了一种采用分段指数型函数的转速滑模观测器，提升了永磁同步电机的稳态控制性能。文献[19]通过扰动观察法对PMSG 的电磁转矩进行控制，实现风机的最大功率跟踪控制，但该控制是局部最优的。为了实现全局最优，文献[20]提出自适应切换叶尖速比法和爬山搜索法的最大功率跟踪控制，但该方法高度依赖于风速测量装置的精确度和可靠性。

为了进一步提升风机并网控制系统的控制性能和鲁棒性，文献[21]针对永磁直驱风力发电系统设计了一种基于最佳叶尖速比控制策略的自适应积分滑模控制器，有效抑制了滑模控制器的输出抖动，提升了鲁棒性。为了提升风机稳态性能，文献[22]采用萤火虫算法对永磁直驱风力发电系统的风速进行估计和补偿，但由于该文献估计模型具有较大计算量，难以实现在线计算。文献[23]通过滑模观测器估计永磁直驱风机的转矩和转速，在线求解风速有效值，对风机控制进行补偿。然而，其开关函数类型的切换函数导致观测器输出抖动加剧，且在线计算量大，导致风机控制的暂态性能下降。文献[24]设计了基于模糊神经控制算法与粒子群优化算法的复合控制器，实现风力发电系统的最大功率跟踪控制。同样，其较大的在线计算量导致实施难度较大。

在前述研究的基础上，本文提出一种结合滑模观测器和查表法的有效风速估计方法，主要创新点在于：根据永磁同步发电机输出电流和电压的测量值，设计了电流滑模观测器和机械转矩滑模观测器。为了降低计算量，在从观测器中提取出转速和机械转矩的观测值的基础上，通过查表法得到有效风速度的估计值，并将该估计值用于修正风力发电系统的最大功率跟踪控制。所提方法在提高系统对风能利用率的同时，降低了计算复杂度进而减少控制器的在线计算量，具有一定的工程应用价值。

1 直驱风机并网系统模型

本文提出的基于有效风速估计的永磁直驱风力发电并网系统拓扑如图1 所示，通过背靠背变流器将风力发电系统中PMSG 产生的频率和电压幅值可变的交流电变换为并网需的交流电。通过利用风速、风机转速、叶片半径、桨距角等数据，可计算得风力机从风能中转换得到的机械功率如式（1）：

式中：Pm为风力机输出的机械功率；ρ为空气密度；Rrotor为风力机叶片的半径；vw为风速测量值；Cp(λ,β)为风能利用率函数；λ为风力机的叶尖速比，其值为λ=ωmRrotor/vw；ωm为风力机的机械转速；β为风力机的叶片桨距角。

利用风机空气动力学特性对风能利用率函数Cp建模如式（2）所示：

式中：C1～C6为工程经验常数，其值分别为：C1=0.517 6，C2=116，C3=0.4，C4=5，C5=21，C6=0.006 8；λi为关于λ，β的函数，其工程经验表达式为

图2 为在不同β值下，风力发电机的风能利用率Cp与λ的关系曲线。

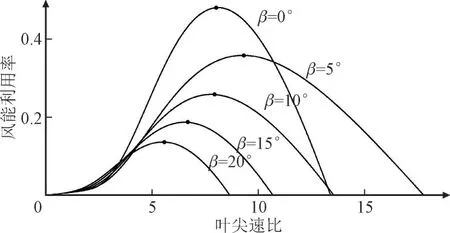
图2 风能利用率与叶尖速比的关系曲线Fig.2 Curve of Cp versus λ

为了使风力机风能转换效率达到最高，同时降低风力机叶片变桨频次，延长使用寿命，在额定风速以下，采用固定桨距角与调节转速的方式进行最大功率跟踪控制。额定风速以上，在转速调节范围有限的情况下，通过固定转速与调节桨距角的方式进行额定功率输出控制。

在两相静止坐标系(α-β)下的PMSG 动力学模型更容易对有效风速进行估计，因为其中含有风机转速和位置信息。在两相静止坐标系中的建立PMSG 的状态空间动力学模型如式（3）所示：

式中：iαs和iβs为定子绕组的输出电流；uαs和uβs为定子绕组的端电压；Ls和Rs为PMSG 定子绕组的电感和等效电阻；J为风力机转子与发电机转子总惯量；D为阻尼系数；Tm和Tg分别为PMSG 的机械转矩和电磁转矩；θe为发电机的转子位置；ωe为转子的电角速度；eαs和eβs分别为定子绕组的感应电势，表达式如式（4）所示：

式中：ψm为定子绕组轴与转子直轴平行时的峰值磁通。

2 有效风速滑模观测器的设计

对有效风速进行估计的永磁直驱风力发电系统如图3 所示。

图3 基于滑模观测器的风机控制框图Fig.3 System configuration of wind turbine control based on sliding mode observer

图3 中，vab，vbc为PMSG 输出的线电压；iabc为PMSG 定子绕组输出的三相电流；vα，vβ，iα和iβ为PMSG 端电压和输出电流在两相静止坐标系中的表达式；为PMSG 的反电动势估计值；，θe分别为机械转速和相位估计值，为PMSG 输出电流的电磁转矩电流分量估计值，为PMSG 的机械转矩估计值。通过滑模观测器对定子绕组在(α-β)坐标系中的反电动势进行观测，利用锁相环提取出反电动势中包含的转子转速和相位信息，进而可以得到定子电流中的转矩电流和励磁电流分量。在观测出电磁转矩的基础上，通过滑模观测器得到风力机的机械转矩观测值。最终通过查表法得到有效风速的估计值。

2.1 电流滑模观测

将式（4）中的电气方程组用矩阵形式表示为式（5）：

式中：A和B为系统矩阵；x=[iαsiβs]T为状态向量；为x的导数；u=[uαsuβs]T为输入向量；h(x,u,t)=为扰动输入向量，假设h(x,u,t)为有界向量。

电流滑模观测器的表达式如式（6）所示：

式中：Li为电流滑模观测器的反馈增益，其决定了滑模面的收敛速度；是电流的观测值；为电流观测值的导数；sat(∙)为饱和函数。

为了减小电流滑模观测器的抖动，观测器中切换函数的饱和函数如式（7）所示：

式中：Δ 为饱和函数的“边界层”；k为常数，表示饱和函数输出值上升区间的斜率。

当观测误差处于“边界层”之内时，电流滑模观测器的反馈呈线性化，从而削弱了观测器在观测误差趋于零时的抖动。

由式（5）与式（6）相减得滑模电流观测误差方程如式（8）所示：

式中：ex为滑模观测器的电流观测误差，其值为滑模观测器的电流观测值和电流测量值x的差；为滑模观测器的电流观测误差的导数；Li为滑模观测器的反馈增益。

当满足存在条件时，电流滑模观测器会将状态轨迹约束在滑模面附近，即满足式（9）：

式中：Si(ex)为电流观测误差的向量。

为了分析滑模状态观测器的稳定性，选取Lyapunov 函数如式（10）所示：

式中：V为Lyapunov 函数。

由式（10）可知，Lyapunov 函数是正定函数，为保证电流滑模观测器的稳定性，只需调整Li使电流滑模观测器满足式（11）：

联立式（5）、式（6）和式（11），可得增益Li的取值范围为：

当Li满足式（12）时，式（6）状态轨迹会在设定的状态轨迹Si(x)=0 附近滑动，即≈0，ex≈0 。且滑动具有渐进稳定性。在滑模面附近，根据等效控制方法，可近似认为式（13）等式成立：

式中：和为两相静止坐标系下PMSG 的等效反电动势。

利用锁相环从和中提取PMSG 转子的电磁角速度和相位，通过Park 变换得到(d-q)坐标系下定子电流的电磁转矩电流分量。风力发电系统中PMSG 的电磁转矩估计值为：

式中：p为PMSG 的定子绕组极对数。

2.2 机械转矩滑模观测

基于滑模观测器的机械转矩观测方程如式（15）所示：

式中：为转子的电角速度的估计值；LT为PMSG 的机械转矩滑模观测增益；eω是机械转速的估计误差。

由式（5）和式（15）得观测器的观测误差方程如式（16）所示：

式中：为机械转速的估计误差eω的导数。

由于电流滑模观测器到达滑模面时近似认为=Tg，此时式（16）可化简为式（17）：

转速滑模观测器的滑模面为：

同样，由Lyapunov 稳定性判据得使转速滑模观测器稳定的LT范围为：

当转速观测方程式（16）的状态满足式（18）时，由等效控制原理得机械转矩的观测值为：

2.3 有效风速估计

风力涡轮机产生的机械转矩为式（21）所示：

通常，在PMSG 的控制中桨距角β是已知的。则可由式（1），式（2）和式（21）联合得到关系式，如式（23）所示：

通过对式（23）进行离线计算，存储对应β值的Tm和ωm的关系，经查表得到对应的有效风速的估计值，如式（24）所示：

将式（24）中的风速估计值用于修正风力发电系统中的风速测量值，提升风力发电系统在风速传感器失效或风速传感器测量出现较大误差等情况下的鲁棒性。

3 仿真分析

为了验证所提基于滑模观测器的永磁直驱风力发电机鲁棒控制策略，基于Matlab/Simulink 平台，建立了PMSG 风力发电系统的仿真模型，其框架如图3 所示。PMSG 风机经两电平背靠背变流器并网，具体参数如下：风机额定功率2 MW，定子额定电压690 V，额定机械转速2.1 rad/s，额定风速12 m/s，定子等效电阻0.005 Ω，定子电感1.25 mH，磁链7.5 Wb，极对数30，风机半径35 m，直流母线电压额定值1 000 V，电网电压10 kV，变流器开关频率10 kHz。

为了验证本文所提有效风速估计方法对风力发电机并网控制鲁棒性的影响，设计了在1 s 时刻风速传感器发生严重故障时的仿真工况，如图4 所示，图4 中的波形从上至下依次为有效值风速测量值与观测值对比、叶尖速比估计值、风力机机械转矩估计值、风能利用率的估计值、并网电流波形。由图4（a）可看出，风速在t=2 s 时刻发生9 m/s 到11 m/s 的阶跃变化，从滑模观测器中得到的有效风速估计值几乎与实际有效风速一致。使用有效风速观测值，在线对风机并网控制中因缺失风速测量值造成的相关状态量误差进行补偿，实现在风速传感器出现严重故障的情况下，仍能够对风力发电机进行最大功率跟踪控制。该方法降低了风力发电并网系统在运行过程中对风速传感器的依赖，提升了系统在风速传感器故障时的鲁棒性。

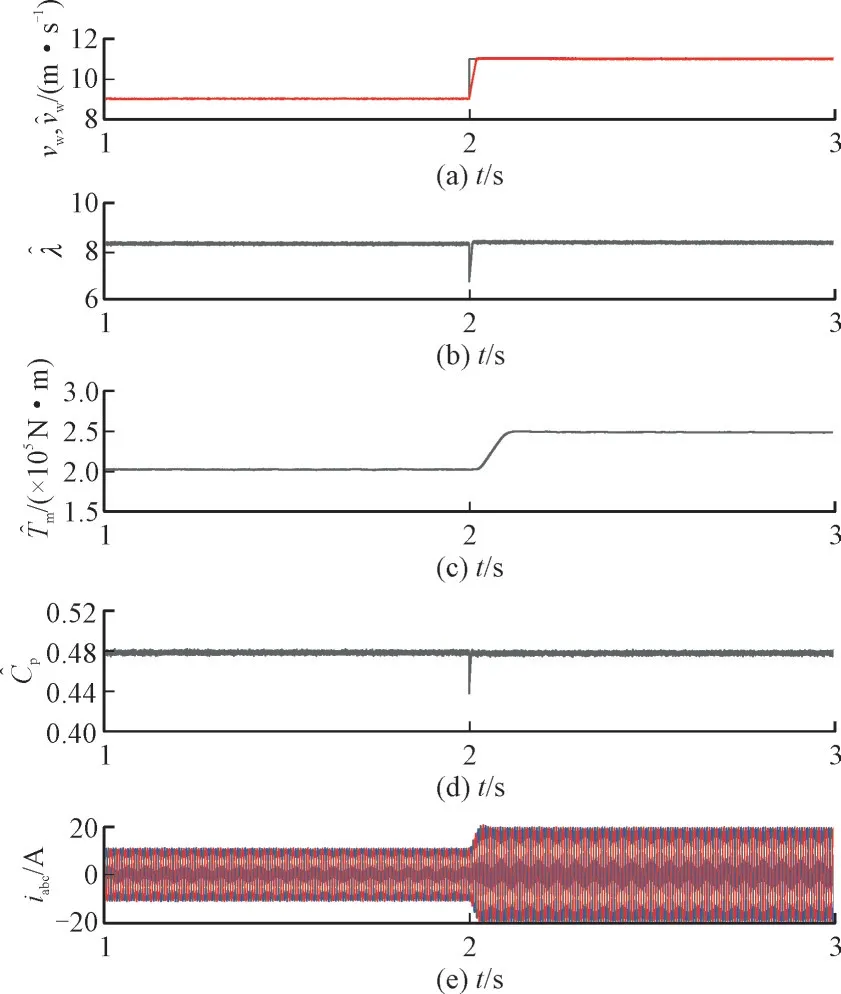
图4 风速传感器故障时的风机状态估计Fig.4 Wind turbine status estimation in case of wind speed sensor failure

为了验证所提方法在风速发生多次缓慢变化的工况下对风机鲁棒性的提升，图5 设定了在2～14 s 内风速发生连续变化的工况。

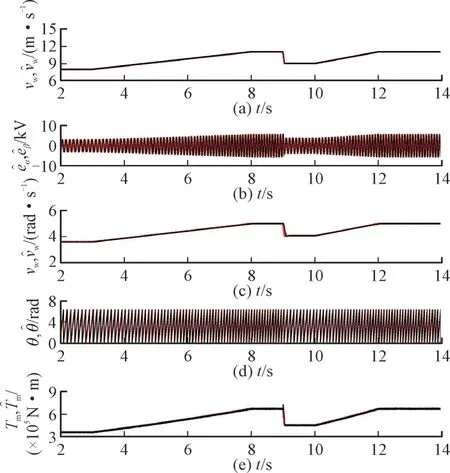
图5 风速传感器故障时的风机状态估计Fig.5 Wind turbine status estimation in case of wind speed sensor failure

图5 中从上至下依次为有效风速、反电动势、转子转速、转子实际位置和观测位置对比波形、机械转矩实际值和观测值对比波形，红色和黑色波形分别为实际值和估计值。对风力发电机机械转矩的估计误差保持在8 000 N∙m 之内，转子转速估计误差的绝对值小于0.3 rad/s，然后通过查表法得到有效风速的估计值。可实现加快有效风速观测的收敛速度，提高对风力发电机转速的精确控制，进而提高风能利用率。

图6 设定了在一段时间内风速发生连续阶跃变化的工况。

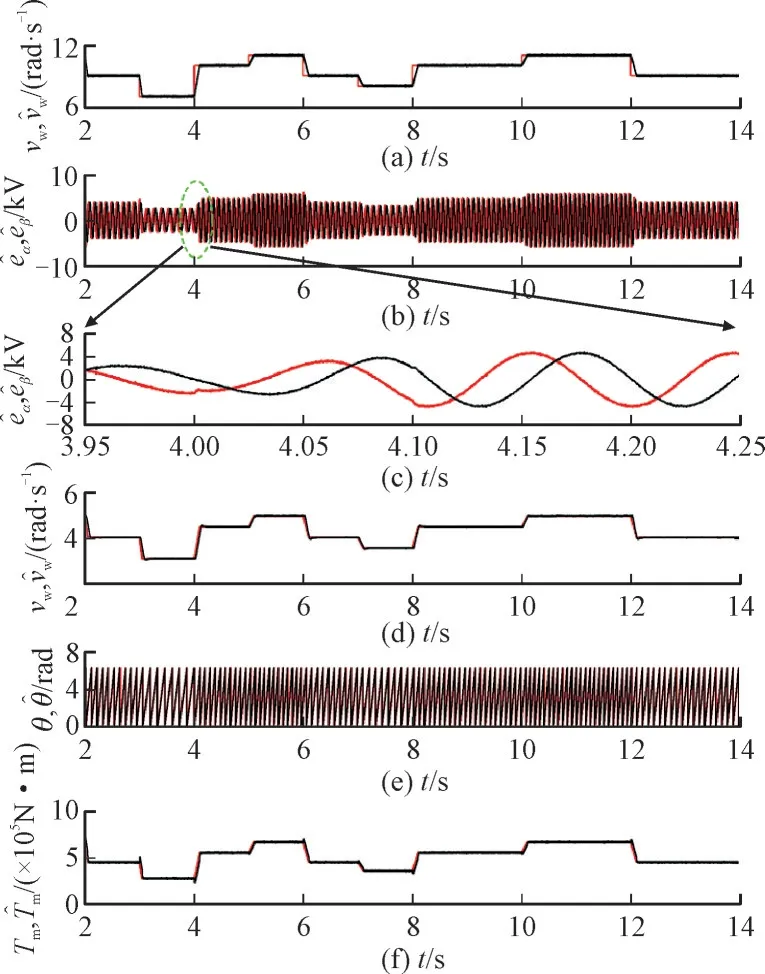
图6 风速连续阶跃变化的风机状态估计Fig.6 Wind turbine state estimation with continuous step change in wind speed

图6 中自上至下分别是有效风速实际值和估计值对比，反电动势估计波形、反电动势观测值局部放大波形、转子实际位置和观测位置对比波形、机械转矩实际值和观测值对比波形、机械转矩真实值和观测值对比波形。通过对比实际和观测得到的波形可知，通过滑模观测器可实现对风力发电机中关键变量进行较为准确的观测，比如对发电机转速的稳态观测误差降至±0.2 rad/s 以内，可降低对转速传感器的依赖，提高转速控制的鲁棒性。最为关键的是，可通过查表法实现对有效风速较为准确的稳态观测，降低观测误差至±0.5 m/s 以内，降低了对风速传感器的依赖。实现了提升风力发电机并网控制鲁棒性的同时，有效提升对风能的利用率。

4 结语

针对永磁直驱风力发电并网系统输出功率受风速测量精确度影响这一问题，本文提出了一种基于有效风速滑模观测的风力发电系统控制策略，可实现对永磁直驱风力发电系统的鲁棒控制。通过设计定子电流滑模观测器，从中提取出永磁同步发电机的定子反电动势和转子相位估计值，进而得到电磁转矩的估计值。在得到转速和电磁转矩观测值的基础上，设计滑模观测器对机械转矩进行观测，结合查表法对有效风速进行快速估计。利用有效风速观测值对永磁同步风力发电机的风速测量误差进行控制补偿，可实现在风速测量存在误差或风速传感器失效的情况下对永磁直驱风力发电机的鲁棒控制。