块石和混凝土排垫保护下海底管道落锚撞击变形响应研究

臧志鹏，许 振，邹 星，侯 静

（1.天津大学 水利工程仿真与安全国家重点实验室，天津 300350；2.天津大学 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室，天津 300350；3.中海油研究总院有限责任公司，北京 100028）

海底管道是海上油气开发的重要输运方式，具有稳定性高、营运成本低等优点，但海底管道一旦发生事故，修复工程比较复杂，造成的经济损失和对环境的影响巨大。已有统计资料表明：大部分的海底管道泄漏污染事件和生产损失是由于抛锚等海事活动导致的管道破坏所引起［1-2］。近些年来随着海上油气资源开发以及海上航运业的快速发展，海底管道穿越航道的情况逐渐增多。因此，有必要对穿越航道的海底管道的防护形式及其在落锚撞击下的变形响应进行研究［3-4］。

对于离岸区域的海底管道一般采用后挖沟自然填埋的保护方式，通常处于半裸露状态或者覆盖于原位海床土之下。针对此类海底管道的落物撞击变形响应开展的研究较多，主要包括宏观的凹陷和屈曲以及微观的应力应变两方面。Arabzadeh 和Zeinoddini［5］研究了在内压存在的情况下海床性质、埋置深度、撞击速度和管内动态波等因素对裸露海底管道截面变形响应的影响。Zeinoddini 等［6］研究内部压力、端部固定条件、撞击物形状、埋置深度和海床土性对海底管道凹陷深度的影响。娄敏和明海芹［7］研究结果表明：相同坠落物能量的情况下，悬空管道的凹陷损伤深度与裸露管道的相比偏小。王懿等［8］基于耦合欧拉—拉格朗日方法（CEL）研究了土壤特性、落锚速度、锚身重力和埋设深度等参数对管道撞击塑性变形的影响。黄启峰等［9］研究了不同海床条件、水深、坠落高度下楔形落物对海底管道表面应变响应的影响。崔鹏等［10］研究了坠物质量、高度、形状、水深以及海床土性等因素对海底管道轴向与环向应变响应的影响。Jiang等［11］研究了撞击速度、坠物质量、坠落高度、埋置深度等因素对受撞击管道模型横向和纵向截面变形的影响。Shin等［12］通过有限元方法研究了海床土性、落锚质量与高度、管道埋深等对管道应变极值和发展历程的影响。

对于裸露管道或者埋土管道受到上方坠物的直接冲击作用，前人做了大量的试验和数值研究。然而在实际工程中，在穿越航道的海底管道上方一般不采用原土回填，而是会铺设防护结构以防止碰撞损坏［3］。闫澍旺等［13］对块石防护层下海底管线的落物撞击损伤机理开展模型试验研究。邱长林等［14］基于有限元和离散元方法研究了冲击荷载对块石保护层下海底管线的作用影响。张萌萌等［15］基于模型试验获得了冲击荷载作用下抛锚高度、管道埋深、堆石材质等参量对管道响应的影响。目前多数的海底管道还是以块石防护为主要手段。余志兵等［16］针对一种新型柔性防护垫对海底管道的保护效果开展了试验研究，对其防护机理和效果进行了论证。张一平等［4］在块石层的基础上，提出了增加混凝土排垫、橡胶垫等不同方案，并通过试验进行了初步比选，但没有开展系统的研究工作。

由于混凝土是常见的水工结构材料，耐久性优良，将混凝土块体通过高强度绳索串联起来的排垫结构具有良好的缓冲表现，且具有较好的经济性和实用性，因此，这里将对块石+混凝土排垫的方案开展详细研究。同时目前对于管道落锚冲击的数值模型，多数为单一覆盖土层以及块石防护层，而对于有2种以上防护层方案的数值模型还未见到。基于ABQUS 建立有限元数值模型，针对碎石层+混凝土排垫防护方案下海底管道受落锚撞击问题开展研究，分析不同因素，包括管道壁厚、内压、落锚质量和撞击速度等对管道凹陷变形和应变响应的影响，为海底管道防护方案设计提供科学依据。

1 数值模型建立

1.1 材料本构关系及参数

研究针对块石+混凝土排垫防护下海床中海底管道在落锚冲击下的变形响应问题开展研究，涉及到了船锚、块石、混凝土块体、海底管道以及海床土体多种材料的模拟。数值模型中将船锚和块石按照刚性体设置，其余材料的本构模型如下：

1）土体本构模型

海床土体在落锚撞击过程中为弹塑性变形，采用Mohr-Coulomb（M-C）模型，该模型在遇到土体大变形时不会出现数值不稳定的现象［17］，M-C模型的剪切屈服面函数和塑性势面函数见式（1）和式（2）［18］。

表1 土体本构模型主要参数Tab.1 Main parameters of soil model

2）海底管道本构模型

海底管道采用Ramberg-Osgood模型［19］，该模型将金属材料的总应变εtotal分为弹性应变εe和塑性应变εp：

其中，E0为初始弹性模量；K为应变硬化相关系数，n为应变硬化指数。采用X52 型管线钢，其相关参数见表2。将管道参数代入式（3）并做变量替换后得到本构模型方程：

表2 X52管道主要参数Tab.2 Main parameters of X52 pipeline

表3 C30混凝土主要模型参数Tab.3 Main parameters of concrete C30

由于Ramberg-Osgood 模型适用于材料在静载或准静载作用下，而钢材材料参数在高速变形条件下将发生较大的变化。因此，管线材料还需要采用弹塑性Cowper-Symonds（C-S）模型［20］来描述高应变率下的应变关系变化，其本构方程见式（5）［21］。

其中，σs为材料屈服应力；ε̇为等效应变率；M和n为模型参数，文中取M=40.4，n=5［15］。

3）混凝土本构模型

混凝土的损伤理论目前最常用到的是《混凝土结构设计规范》（GB 50010—2010）［22］中的拉伸压缩塑性损伤模型，考虑了混凝土在未受力时初始裂纹的存在以及损伤积累导致的裂纹扩展，包括拉伸损伤的软化以及压缩损伤的硬软化［23］。混凝土损伤模型屈服函数使用Lubliner 等［24］的屈服函数，经Lee 和Fenves［25］修正，考虑了拉伸和压缩强度的演变。屈服面的演变受等效拉伸应变ε͂plt和等效压缩应变ε͂plc控制，有效应力的屈服函数形式为：

1.2 数值模型建立

研究基于ABAQUS 建立有限元数值模型，对船锚、海底管道、海床土体、块石层和混凝土排垫进行模拟。土体在受到撞击作用时将产生大变形，因此土体使用欧拉单元，而其他部件使用拉格朗日单元，模型采用耦合欧拉—拉格朗日（CEL）分析法。CEL是一种广泛用于处理有限元大变形问题的网格处理办法。在欧拉分析中，连续体的运动由时间和空间坐标的函数表示，欧拉网格保持未变形，材料可以在网格中自由移动［7］。拉格朗日对象可以在欧拉区域内移动，直到接触到欧拉材料。由于离散元（DEM）等离散体模拟方法均不能和CEL 方法耦合，因此这里的块石层采用ABAQUS 装配模块中的阵列功能，采用球形单元近似块石体，在3个坐标方向上对球形块石体进行复制生成阵列。在落锚撞击块石层前，给予其充分的时间自由塌落调整位置，以形成稳定的块石层结构。混凝土排垫为一系列立方体单元通过尼龙复合材料串成的柔性排状结构，在模型中同样采用阵列功能进行混凝土块体单元复制，块体单元之间利用尼龙复合材料连接，并通过装配模块中的“合并/切割实体”功能生成整体混凝土排垫，混凝土块层合并后如图1（a）所示。研究中，船锚和块石层均设置为刚性体，不考虑变形，仅模拟其运动过程。

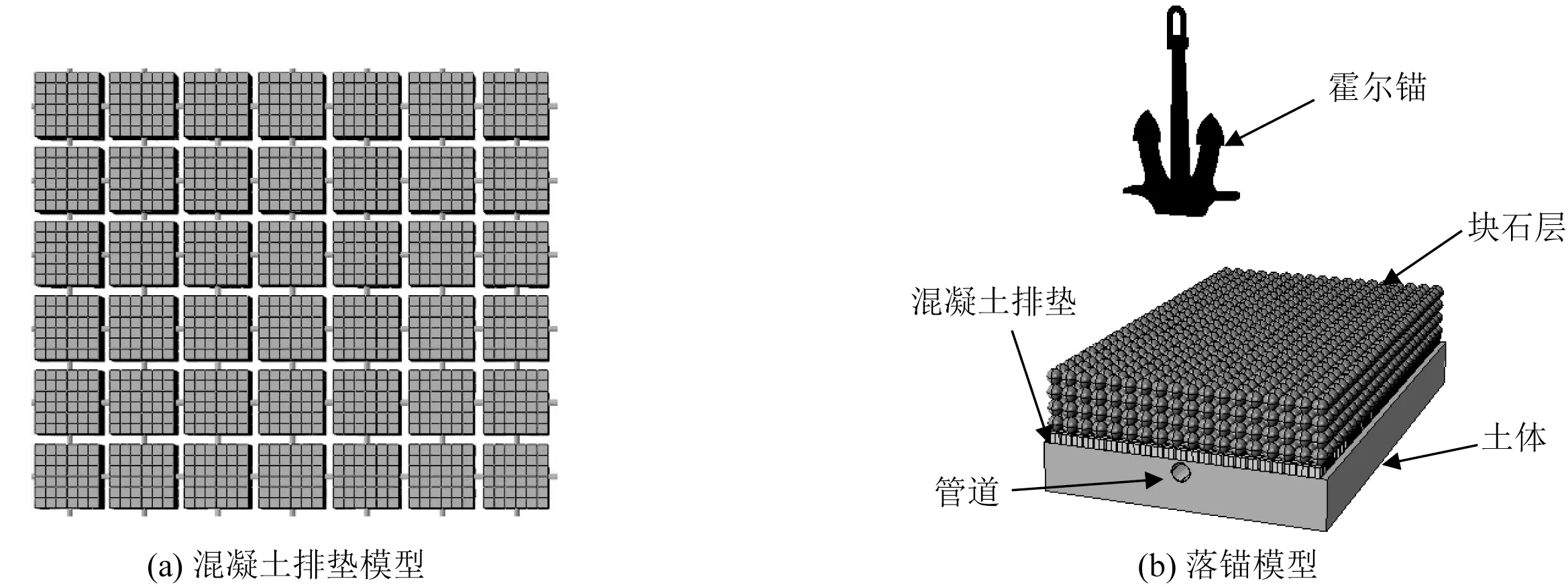
图1 块石+混凝土排垫防护方案模型Fig.1 Numerical model for rock berm + concrete mattress protection

由于管道属于薄壁结构，同时为了便于管道轴向和环向相关变量的输出，海底管道模型采用S4R 四结点减缩积分壳单元；混凝土块体单元连接的尼龙复合材料采用B31 两结点空间线性梁单元；土体采用EC3D8R 八结点线性欧拉六面体减缩积分单元；由于模型采用Explicit 动力显示分析，为尽可能真实反映船锚形状，船锚采用C3D10M十结点修正二次四面体单元；模型在块石层和海床土体的计算域外边界采用刚性壁面进行约束，以模拟无限大区域的约束效果，该壁面采用R3D4四结点三维双线性刚性四边形离散刚体单元；其余部件采用C3D8R八结点线性六面体减缩积分单元。

数值模型基于原型实际尺寸建立，底部海床土体模型尺寸为1 467.5 mm×8 385 mm×14 000 mm（高×宽×长），网格尺寸为70 mm。船锚尺寸采用规范《霍尔锚》（GB/T 546—2016）［27］中质量16 t的A 型霍尔锚原型尺寸，网格密度取300 mm。落锚撞击接触面长度与土体宽度比值小于1∶5，因此，土体模型边壁效应可以忽略。管道尺寸为559 mm×15.9 mm×14 000 mm（直径×壁厚×长度），撞击点附近轴向长度网格尺寸加密为40 mm，其余位置为100 mm；混凝土块体单元尺寸为300 mm×300 mm×300 mm（长×宽×高），网格尺寸取为50 mm；尼龙复合材料连接绳单元尺寸为50 mm×28 mm（长×直径），梁单元网格尺寸取为5 mm。通常在近岸处海底管道块石护面层设计质量为100～200 kg［4，16］，文中块石单元采用球体单元进行等效，按照密度2 700 kg/m3计算，则球体单元直径范围为420～520 mm。模型中球体单元采用460 mm 直径，在实际的取值范围之内，网格尺寸为150 mm。模型各主要部件的详细尺寸与网格密度见表4，数值模型如图1（b）所示。

表4 模型各部件尺寸与网格密度Tab.4 Dimension and grid size of each component in model

数值模拟的分析步类型为动力显示分析，线性体积黏性系数和二次体积黏性系数分别取值0.06 和1.2。模拟时间长度取1.1 s，前1.0 s 为块石层稳定时间段，后0.1 s 为落锚撞击过程时间段。由于研究问题的对称性，为提高计算效率，只取原型尺寸的一半进行建模，在管道、防护层的边界上额外施加一个对称约束；海床欧拉体3个方向的约束条件不再是位移约束条件，而是将对应方向的速度约束为0。对于模型中的管土切向接触采用摩擦系数为0.3的罚接触算法，法向压力过盈采用“硬”接触算法，并允许接触后分离。考虑到欧拉土体与其他拉格朗日体必须采用通用接触，且块石体与船锚接触面复杂，因此，文中其余各部件的相互接触属性统一采用通用属性。

2 模型有效性验证

埋置于海床土体中的海底管道，在上方块石和混凝土排垫的保护下，受到落锚的撞击，涉及到各个物体和材料之间能量的转化，但对于总的撞击系统来说，仍需遵守能量守恒定律。文中所有模型计算过程中总能量值Etotal始终保持为一个常数，变动幅值小于5%，因此模型总体上满足能量守恒定律。

2.1 裸露海底管道受冲击模拟

Wang 等［28］试验模拟了刚性落锤冲击裸露悬跨管道的过程。管道长度2 000 mm、外径219.1 mm、壁厚10 mm；两端固定在支座上，悬跨长度为1 800 mm。落锤质量为1 350 kg，自由下降高度为3.4 m。试验分为两组，一组内部填充超轻水泥复合材料，简称CCFP；另一种内部无填充，简称HSP。支座上设有65 mm 宽度的钢箍限制钢管试样的抬升。数值模型中采用了与试验填充材料抗压强度接近的C65 混凝土，密度设为1 460 kg/m3，钢管弹性模量为207 GPa，泊松比为0.3，屈服应力约416 MPa。数值模型如图2所示。

图2 CCFP和HSP工况下的模型网格划分Fig.2 Meshes for CCFP and HSP cases

数值模拟得到了CCFP 和HSP 工况下管道撞击点截面底部的垂向位移过程曲线wg，并与试验结果进行比较，如图3所示。在CCFP工况下，数值模拟结果与试验结果历程曲线形式基本一样，误差小于8%；HSP工况下的最大位移值相同，但数值模拟结果的最大位移值出现时刻略有提前，总体上对于位移的模拟效果较好。图4（a）为CCFP工况下管道1/4跨处底面位置的应变ε历史曲线，图4（b）为HSP工况下管道跨中侧面位置处的塑性应变ε 历史曲线。可见，文中有限元方法模拟计算得到的管道变形与应变值与物理试验结果吻合很好，证明了当前数值模型的可靠性。

图3 管道撞击点截面底部的位移历史曲线Fig.3 Time histories of displacement of the bottom of the pipeline

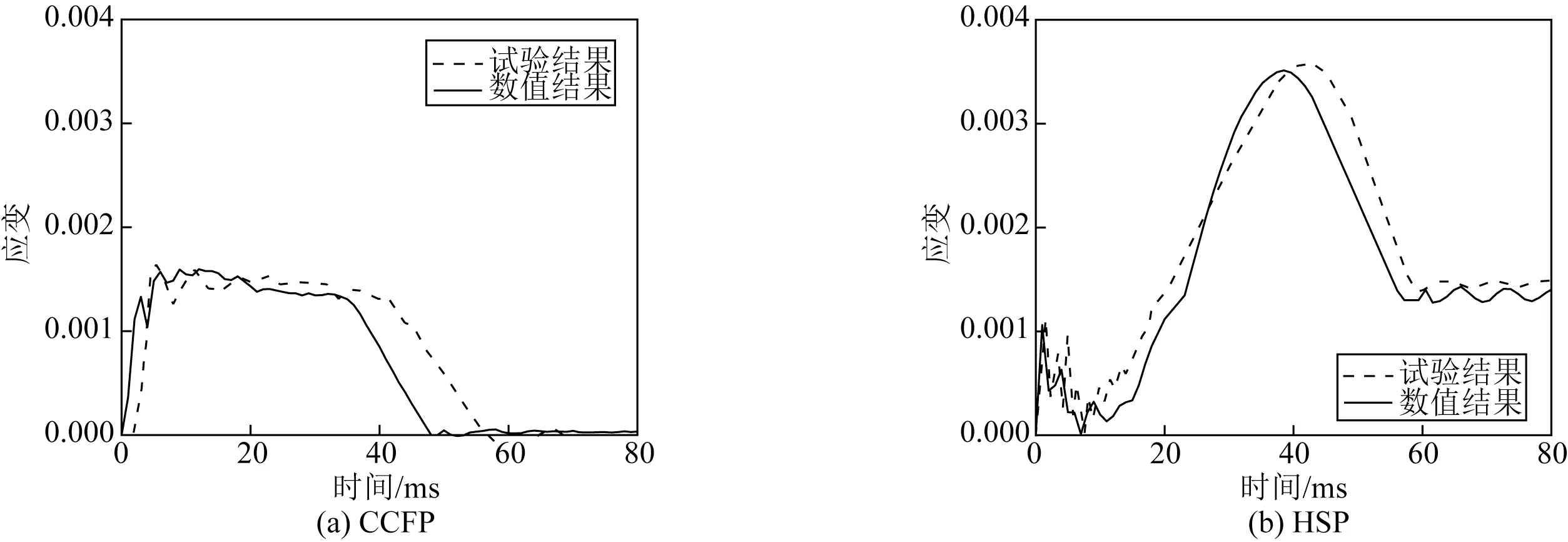
图4 特征点处塑性应变历史曲线Fig.4 Time histories of plastic strain at typical points

2.2 土体覆盖下海底管道受冲击模拟

Jiang等［11］试验模拟了埋置于砂土海床中的管道在下落钢球撞击下的损伤问题，测量了撞击产生的最大凹陷深度。管道模型长度为1 000 mm，外径为63 mm，厚度为1 mm。基于ABAQUS 建立与试验相同的数值模型，采用Mohr-Coulomb 模型描述砂土的本构关系，砂土密度为1 800 kg/m3，弹性模量为5 MPa，泊松比为0.3，摩擦角为36.5°，膨胀角为2°，黏聚力取为0.1 kPa。管道的相关参数见表5，并添加Cowper-Symonds 模型描述与应变率相关的相应修正，相关参数为：M=40.5，n=5，数值模型如图5（a）所示。以2.0 kg 落球，1.0 m 坠落高度工况为例，管道竖向位移云图如图5（b）所示。

图5 落球撞击管道数值模型及结果示意Fig.5 Sketch of numerical model and result for pipeline impacted by a dropped ball

表5 管道模型材料参数Tab.5 Material parameters of pipe model

不同钢球质量和坠落高度下，管道上最大凹陷深度的数值结果与试验结果对比如图6所示。总体上，数值模型和物理模型试验结果符合较好，最大相对误差在10%以内。这些差异主要是由于土壤强度的不均匀性造成的，因为砂土需要在每次冲击试验之前进行固结。在试验中很难保持土壤固结度和均匀性完全相同，这将直接影响土壤强度。

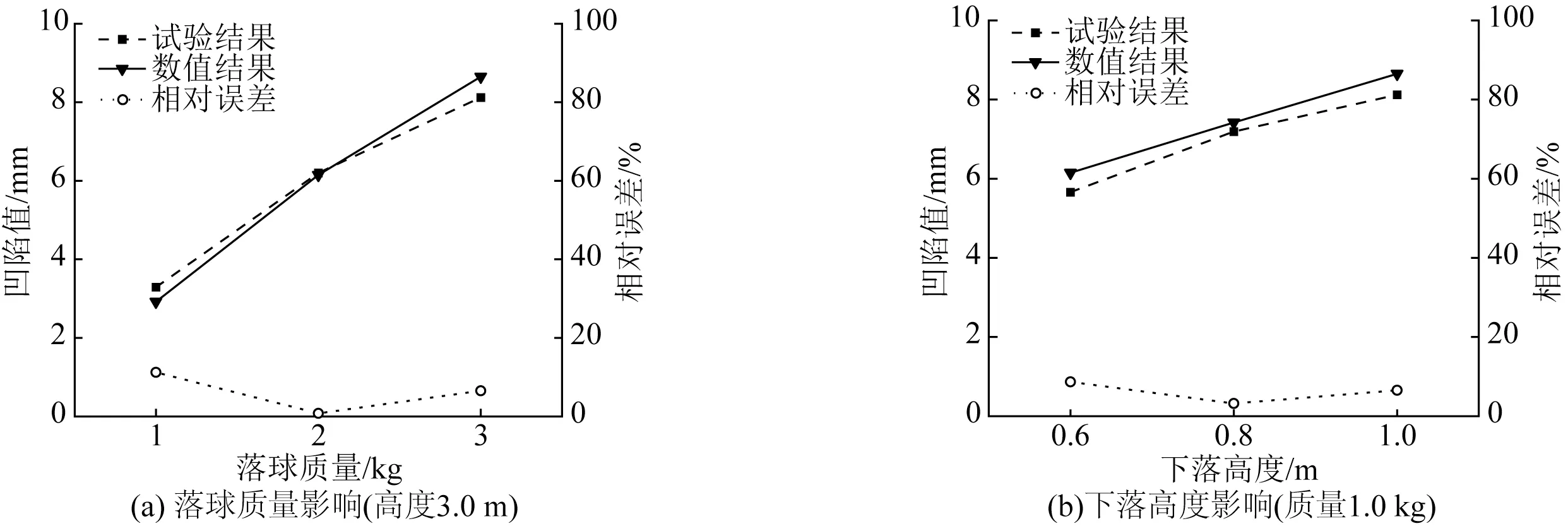
图6 管道表面最大凹陷深度结果对比Fig.6 Comparison of the maximum dent depth between experimental and numerical results

2.3 块石+混凝土排垫防护下海底管道受冲击模拟

张一平等［4］通过模型试验对几种防护方案包括块石+混凝土排垫方案下的海底管道应变响应进行了测量。试验中管道模型采用外径为40.2 mm 的PVC 管，壁厚为5.9 mm，长度为2 000 mm；抗弯刚度为2.36×102N·m2，管道及配重总密度为3 010 kg/m3。防护层的总厚度为130 mm，其中块石层厚度65 mm，混凝土排垫厚度65 mm；霍尔锚模型质量为4.39 kg，下落高度1.0 m。管道模型在上、下、左、右4个表面沿轴向各设置7 个光纤应变传感器测点，间距为250 mm。文中建立与试验相同的数值模型，模拟落锚的过程以及海底管道上的应变分布。数值模型设置参照图1。

图7 给出了海底管道上、下表面最大轴向应变分布数值结果与试验结果的比较。上表面在撞击点（0 m位置）处于轴向压缩状态，出现最大压应变，在距离撞击点处约1/3管道长度处出现最大拉应力，这是由于管道在落锚撞击下，发生类似于固支梁在集中荷载作用下的变形状态。由于受到海床的约束，管道变形应变沿长度方向逐渐衰减，在离撞击点最远端处（1 m 位置），管道应变接近为0。下表面的轴向应变分布基本与上表面相反。数值模拟结果与试验测量结果的趋势和数值符合很好，可以用于原型尺寸的块石+混凝土排垫防护性能的系统研究。

图7 块石+混凝土排垫防护下管道表面轴向应变分布Fig.7 Distribution of axial strain on the pipeline with rock+ concrete mattress

3 数值结果和讨论

3.1 海底管道保护层有效性分析

为了进一步验证块石+混凝土排垫防护形式具有更加优良的缓冲性能，首先比较了无防护层（N）、块石层（R）和总厚度相同的块石层+混凝土排垫（CR）3 种防护形式下的管道应变和最大凹陷值。数值模型建模均采用原型尺寸，参数见表4。船锚采用16 t 的霍尔锚，下落高度为20 m。3 种情况下管道受撞击瞬间变形数值结果如图8所示。管道表面最大凹陷值和最大应变值统计如表6所示。无防护层情况下管道最大凹痕值和最大应变值均比块石层和块石+混凝土排垫防护情况下高数倍。比较块石层和块石层+混凝土排垫两种防护方式，后者的管道最大凹陷值比前者减少了约15%，而后者的管道最大拉伸和压缩应变比前者分别减少了约88%和65%，这主要是由于混凝土块层的弹塑性网状结构在冲击力作用下能够储存和耗散更多的能量，使得最终作用在管道上的能量减少。以上结果表明：块石层+混凝土排垫相比于纯块石层防护方案对落锚撞击作用具有更加优良的缓冲效果。

图8 不同防护形式下管道受撞击变形结果Fig.8 Numerical results for deformation of pipeline under different protective schemes

表6 不同防护层下管道的变形响应Tab.6 Deformation of pipeline under different protective schemes

3.2 管道受落锚撞击变形响应基本规律

进一步对块石+混凝土排垫防护方案进行系统研究。图9 为落锚质量16 100 kg、撞击速度为9.8 m/s 情况下管道轴线方向上4个表面的环向和轴向总应变分布。图9中位置坐标0 m代表落锚撞击的位置，14 m为管道远端位置。如图9（a）所示，由于受到船锚撞击的直接作用，管壁的环周向发生拉伸效应，在管道上表面撞击处出现最大环向拉应变值，而管道侧面由于竖直方向的支撑力，环向压应变为最大值；环向应变由撞击点附近到管道端部呈现递减趋势，环向应变主要集中在撞击点附近4 m内的区域；侧表面的环向应变大于上下表面的环向应变。图9（b）中，撞击位置处由于管道产生向下的挠曲，在上表面处出现最大轴向压缩应变，而在下表面出现最大轴向拉应变；管道上下表面轴向应变呈现先减小至相反方向极值后又逐渐沿程减至0的趋势；左右侧面的轴向应变沿程变化趋势与下表面相似，上下表面的轴向应变值要大于侧表面的轴向应变值。在管道应变分布区域上，上下表面的轴向应变在距撞击点10 m左右开始趋近于0，而两个侧面的轴向应变主要发生在3 m 范围内。总体上，管道在落锚撞击下的变形形式与两端固支的简支梁在集中荷载作用下的变形形式相似。图10为撞击后在轴向和环向上的残余塑性应变沿程分布，可见塑性应变主要集中在管道撞击位置1 m附近的区域，而在远处位置的塑性应变基本为0。上表面和侧表面的最大环向塑性应变相对较大，可达±2×10−3；上下表面的最大轴向塑性应变也相对较大，分别为−2×10−3和1.2×10−3。

图9 管道轴线上沿程应变最大值分布Fig.9 Distribution of maximum strain along the pipeline

图10 管道轴线上沿程塑性应变分布Fig.10 Distribution of plastic strain along the pipeline

图11（a）给出壁厚为11.90、13.90、15.90、17.90 和19.90 mm 的管道在撞击过程中的凹陷深度变化历程。落锚的质量为16 100 kg，撞击速度为10.8 m/s，落锚的动能为1 118 kJ；模拟管道在铺设过程的状态，内压设为0.1 MPa，模型的其他参数与上文相同。管道前1.0 s 为船锚下落过程和块石层稳定阶段，此时未发生碰撞，管道凹陷深度保持在0附近。从1.0 s开始，落锚与块石层接触，通过块石层、混凝土排垫依次将撞击作用力传导至管道，在1.03 s时刻管道凹陷深度值达到最大；之后管道发生部分弹性回复；在1.1 s之后趋于平稳，之后仍然保留一定的塑性变形。图11（b）为撞击点处的环向应变与轴向应变历程曲线，二者峰值接近且数值相反，说明撞击点处存在两个数值接近、互相垂直的应变分量。

图11 不同壁厚管道撞击点的凹陷深度与应变历程曲线Fig.11 Time histories of dent depth and strain at impact point for different wall thicknesses of pipeline

3.3 不同因素对管道表面应变值和凹陷深度的影响

这里研究不同管道壁厚时落锚撞击管道的应变值和凹陷深度变化规律。落锚撞击过程中的应变历程和凹陷深度历程曲线见图11。图12（a）为管道撞击点处上下表面的轴向最大应变和塑性应变随壁厚的变化情况。总体上，上表面为压应变，下表面为拉应变；最大应变和塑性应变的变化趋势一致，同时上表面的应变绝对值大于下表面值。环向应变值的变化趋势与轴向应变值相似，这里不再给出。图12（b）将最大轴向应变和最大环向应变值进行了比较，二者变化趋势基本一致，随着管道壁厚的增加，管道截面惯性矩增加，截面抗弯系数增加，因此管道弯曲应变随之越小；同时环向应变的绝对值大于轴向应变绝对值。图12（c）中，随着管道壁厚的增加，管道抵抗冲击变形的能力提升，管道上表面的最大凹陷值随着管道壁厚的增加而减小。

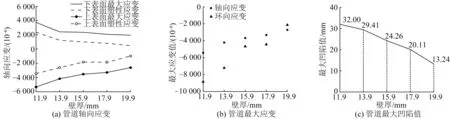
图12 壁厚对管道应变与凹陷值的影响Fig.12 Effect of wall thicknesses on strain and dent depth of pipeline

进一步研究了不同内压情况下落锚撞击管道的应变值与凹陷深度变化规律。内压的变化值为0.1、2、4、6 和8 MPa，管道壁厚为15.9 mm，落锚的质量为16 100 kg，撞击速度为10.8 m/s，动能为1 118 kJ，模型的其他参数与上文相同。由于内压本身会使管道产生一定量的拉伸应变，当内压增加时，管道的环向和轴向拉伸应力也会增加，因此内压产生的拉伸应变也随之增加。图13中的最大应变值和凹陷深度值为落锚撞击和内压共同作用引起的。管道由于内压的存在，使得管道径向抵抗变形的能力提升。相同落锚撞击条件下，随着内压的增加，管道的最大拉应变随之增加、最大压缩应变随之减小，最大凹陷深度也随之减小。

图13 内压对管道应变与凹陷值的影响Fig.13 Effect of internal pressure on strain and dent depth of pipeline

图14 为管道的应变值与凹陷深度值随落锚撞击速度的变化情况。落锚撞击速度分别为7.8、8.8、9.8、10.8 和11.8 m/s，落锚质量为16 100 kg，管道壁厚为15.9 mm，内压为0.1 MPa，其他参数同上文。随着落锚撞击速度的增加，动能也越大，管道受冲击作用也越大，管道上下表面的轴向应变最大值和塑性应变都随之增大；管道两侧面点的环向应变绝对值也不断增大。根据能量守恒定律，船锚从开始撞击管道到船锚下沉位移达到最大的过程中，不计重力势能的损失，船锚的动能将转化为管道的弹性变形能以及塑性变形能，因此初始船锚动能越大，则管道发生的整体形变量越大，同时管道局部凹陷深度值也越大。

图14 撞击速度对管道应变与凹陷值的影响Fig.14 Effect of impact speed on strain and dent depth of pipeline

图15为管道的应变值与凹陷深度值随落锚质量的变化情况。落锚的质量分别为8 398、10 689、13 257、16 100 和19 220 kg，落锚的撞击速度为10.8 m/s，管道壁厚为15.9 mm，内压为0.1 MPa，其他参数同上文。与改变撞击速度的情况相似，管道上下表面的轴向应变最大值和塑性应变都随落锚质量的增大而增大；管道两侧面点的环向应变绝对值也不断增大。根据能量守恒定律，落锚质量越大，初始动能越大，则管道发生的整体形变量越大，同时管道局部凹陷深度值也越大。

图15 落锚质量对管道的应变与凹陷值的影响Fig.15 Effect of mass of anchor on maximum strain and dent depth of pipeline

以上分别研究了落锚质量和撞击速度对于管道应变和局部凹陷的影响，图6 则将管道的应变和凹陷值随落锚动能的变化进行汇总。总体上，相同落锚动能下的管道最大应变值和最大凹陷值基本相同，这也说明管道的变形量取决于落锚的总动能。同时发现，相同动能下，变化落锚质量得到的应变和凹陷值略小于变化落锚速度时的应变和凹陷值。这主要是由于数值模型中船锚密度恒定，当质量增加时，船锚体积增大，与管道上方防护层的接触面积也增大，因而被防护层吸收的冲击动能也略大。而速度的改变过程中，落锚与防护层的接触面积没有发生变化。如果不考虑船锚质量变化引起体积改变的影响，落锚总动能仍然是海底管道上最大应变值和凹陷值的决定因素。

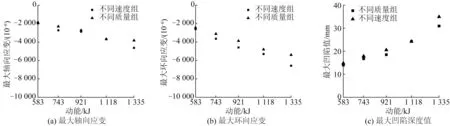
图16 落锚动能对管道变形的影响Fig.16 Effect of kinetic energy of dropped anchor on deformation of pipeline

4 结 语

基于ABAQUS 建立了包含落锚、海底管道、海床土体、块石层和混凝土排垫的复杂数值模型，以A 型霍尔锚撞击为原型实例，研究了落锚撞击下壁厚、内压、落锚质量和撞击速度等因素对管道应变极值和管体凹陷变形的影响。主要结论为：

1）相比较块石层和块石层+混凝土排垫两种防护方式，在落锚撞击中后者防护下的管道最大凹陷值比前者减少了约15%，而后者的管道最大拉伸和压缩应变比前者分别减少了约88%和65%，可以作为穿越航道海底管道的防护方案。

2）由于受到船锚撞击的直接作用，在管道上表面撞击处出现最大环向拉伸应变值，而管道侧面由于竖直方向的支撑力，环向压缩应变为最大值；环向应变由撞击点附近到管道端部呈现递减趋势，环向应变主要集中在撞击点附近4 m 内的区域。撞击位置处由于管道产生向下的挠曲，在上表面处出现最大轴向压缩应变，而在下表面出现最大轴向拉伸应变。

3）在管道应变分布区域上，上下表面的轴向应变在距撞击点10 m左右基本趋近于0，而两个侧面的轴向应变主要发生在3 m 范围内。撞击后在轴向和环向上的塑性应变主要集中在管道撞击位置1 m 附近的区域。

4）随着管道壁厚的增加，管道的最大应变和凹陷深度随之减小；随着内压的增加，管道上最大拉伸应变变大，而最大压缩应变和凹陷深度减小。随着落锚速度或者质量的增加，管道上最大应变和凹痕深度均变大；在相同动能情况下，管道上的最大应变和凹陷值基本相同，也表明落锚动能是影响管道变形响应的控制因素。