基于特征点筛选的渔船轨迹压缩方法及优化

马苏上,王泽宇,刘明剑,2,李 洋,赵文彬

(1 大连海洋大学信息工程学院,辽宁 大连 116023;2 设施渔业教育部重点试验室(大连海洋大学),辽宁 大连 116023)

近年来渔民捕捞经济在海洋经济中日益重要[1],2021年海洋捕捞产值为2 303.72亿元,渔船作为渔民捕捞的工具,加强对渔船的行为监管,是保障渔业健康有序地发展的重要手段[2-3]。渔船在作业过程中呈现出捞区域繁多、分布广、持续作业时间长等特点[4],这就需要在监管过程中,对渔船不同作业特点的轨迹进行差异化分析。目前常用的船舶轨迹跟踪方式是使用船舶自动识别系统[5](Automatic Identification System,AIS)对渔船行驶轨迹进行记录与存储,但在此过程中,AIS系统会产生大量的轨迹数据[6],不仅消耗系统存储与计算资源,还存在大量的冗杂和错误信息[7],不利于对船舶轨迹的有效分析。如海上渔船由于捕捞作业会产生大量的静态信息,此时仅需保留几条有效的信息,就可以有效的反映渔船的作业状态,因此需要采用轨迹压缩方法对渔船轨迹数据进行筛选,从而为渔船行为有效分析提供高精度的轨迹数据支撑。

针对上述需求,国内外的研究学者开展了关于渔船轨迹压缩方面的相关研究,目前船舶轨迹压缩方法大致分为两类[8]:在线轨迹压缩方法;离线轨迹压缩方法。在线压缩算法为局部处理算法,处理速度较快。其中,Keoghe等[9]采用滑动窗口方式实现了在线压缩;文献[10-12]通过在滑动窗口中加入阈值方式来提升压缩效率。但以上方法没有考虑部分特征点对整条轨迹曲线存在轨迹信息量不均衡现象,当删除一些极值点后易造成轨迹失真,不利于渔船轨迹分析;离线轨迹压缩方法,则是对于全局数据进行分析处理,保证了所有轨迹点都需进行判别[13],更适于对渔船轨迹进行分析。Mancini等[14]提出了均匀采样方法,实现轨迹压缩;Douglas等[15]提出的Douglas-Peucker(简称DP)算法,将轨迹的起始点相连接作为基线,根据其余轨迹点到直线的垂直欧式距离来进行轨迹的压缩。在DP算法的基础上,文献[16-17]通过修改数据集、去除数据冗余信息来实现高效渔船轨迹压缩;文献[18-19]考虑了船舶轨迹的压缩形状,有效保留了船舶航行中作业的重要特征信息,减少了算法的时间复杂度。文献[20-21]着重研究阈值对于轨迹压缩的影响,根据不同情况改变阈值,实现更精确的压缩。文献[22-24]通过引入时间维度信息来对渔船航向速度等动态数据进行压缩,能够保留更多的重要动态行为轨迹点。

尽管上述方法对于离线轨迹压缩的处理趋于完善,但目前离线压缩算法无法妥善处理和反映船舶的这些动态变化特征信息,导致其算法运行的时间复杂度较高,且轨迹压缩的误差较大,致使轨迹压缩后存在失真的问题。针对上述问题,本研究提出了FMDP渔船轨迹压缩方法,在保证压缩率的前提下最大程度保留了渔船轨迹的特征信息。

1 算法建立和实现

1.1 FMDP轨迹压缩方法

设渔船在行驶过程中,AIS轨迹点为p(x,y),由轨迹点p所组成的轨迹点集为T。渔船在某一位置长时间停留或移动距离极短的点被称之为停留点,停留点集为ts。

FMDP轨迹压缩方法:首先,将原始轨迹T进行停留点筛选出并计入停留点集ts(ts⊆T),同时,针对渔船行为停留时间较长,造成的差异化停留与转向状态特征,设计压缩轨迹权重机制,对停留点集ts再次筛选;其次,使用加入角度阈值的DP算法进行轨迹压缩处理完成特征点筛选,组成特征点集tr(tr⊆T);最后,取ts和tr的交集为整合点集tA,将tA按照时间顺序的轨迹点串联得到新的压缩轨迹。

1.2 留点筛选

1.2.1 轨迹点间距离

停留是移动对象的基本运动状态,代表着轨迹中具有重要特征的点序列[25]。当渔船停留时可能会因为外界因素或者自身因素发生偏移现象,导致停留点并不是固定的点。为了可以更准确判别轨迹点是否属于停留点,进行如下设定:将某条渔船的原始渔船轨迹点集T依次分成n个船速计算区域,其中每个区域包含五百个AIS轨迹数据点。考虑任意相邻的轨迹点之间距离并不属于直线距离,因此本研究将轨迹点的经纬度坐标转换为笛卡尔坐标,进行距离度量。轨迹点距离d是两个相邻的轨迹点的恒向线[26],其距离公式如下:

(1)

式中:Δx和Δy分别为两个相邻轨迹点的经纬度差值[27],(°);c为结合后续计算所设计的参数系数;r为地球的半径,km;a是用来将经度转换的等量维度系数。

1.2.2 停留点阈值设定

依据不同区域行驶距离与所用的时间,求取出不同区域的平均速度作为该区域渔船行驶速度,并筛选出最慢的行驶速度vmin,并根据AIS数据发送的最短时间间隔与速度vmin,求出最短的距离l0,作为停留点阈值:

l0=vmin×tmin

(2)

式中:l0为最短的距离,km;vmin为行驶速度,km/s;tmin为停留时间,s。

1.2.3 停留点筛选

随后将点集T中的轨迹点pi到pi+1的距离为di,pi+1到pi+2所组成线段距离为di+1,两线段的距离之和为di+di+1,其距离之和根据公式(1)将经纬度转换为笛卡尔坐标系再进行计算。将距离之和与阈值l0进行对比,如果di小于l0则取中间的点pi+1作为停留点,之后继续计算轨迹点pi+1到pi+2,pi+2到pi+3的距离之和与阈值l0进行判定,直至将轨迹点集T中所有符合条件的停留点全部筛选出为止,并将这些停留点组成停留点点集ts。

1.3 特征点筛选

1.3.1 原始DP算法的轨迹特征点筛选处理

(3)

式中:x与y为通过投影将经纬度转化到同一平面坐标的经度与纬度。k和b是笛卡尔坐标系中的常数。

1.3.2 加入了角度阈值的轨迹压缩特征点筛选

传统的DP轨迹压缩方法中,仅考虑了距离特性而忽略了船舶的转向变化特性,无法保证将全部特征点进行筛选,导致压缩后的轨迹不能完整反应出原始轨迹特征。因此为保证船舶的转向信息最大保留,在DP算法原有距离阈值的基础上加入了角度阈值筛选特征点方法。

轨迹点的转向角度由连续的3个AIS点构成,3个AIS点依次相连,所构成线段的角度即为转向角度。设定轨迹点的角度阈值,当轨迹点满足角度阈值条件,但未满足原始DP算法的特征点选择条件时,仍可作为特征点计入特征点集TR。

角度阈值的选取与轨迹压缩率有着密不可分的联系。为了避免选取不合适角度阈值后导致算法对数据的压缩率效率降低,将采取真实渔船轨迹数据进行测算来获得每条船在压缩时的最佳角度阈值,通过对比不同角度下的角度轨迹压缩率,判断出最佳的角度阈值,计算不同角度的范围压缩点的剩余点数目Va与原始轨迹点数O结合求出角度压缩率Ca,其公式如下:

(4)

以2018年10月1日至7日大连世想海洋科技有限公司提供的某条渔船轨迹数据为例进行角度阈值选取。由于该船在此时间段AIS数据庞大,微小的角度变化就会造成压缩率巨大变化,因此该算法分两阶段筛选角度阈值。第一阶段筛选大致范围,规定每10°一个区间,根据峰值挑选出合适的角度范围,如图1所示,当这条渔船转向角在40°至60°以及130°至150°时存在有最大的角度压缩CA,因此需要对于以上两个区间范围继续通过第二阶段进行筛选。

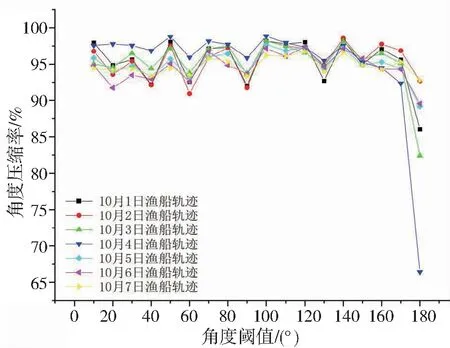
图1 第一阶段轨迹压缩率

第二阶段将挑选出的角度范围再次细分进行二次筛选,以确保压缩率最大化,规定每2°一个区间,同样根据峰值筛选出最佳角度范围,完成最终的角度阈值确立,如图2所示。

注:(a)图为40°至60°区间内的轨迹压缩率,(b)图为130°至150°区间内的轨迹压缩率

1.4 轨迹点集结合处理

1.5 复杂轨迹压缩权重机制

考虑到渔船的作业类型不同,部分捕捞作业花费时间较长,如捕捞金枪鱼和石斑鱼等鱼类,需要在同一地点持续2～3 h的捕捞作业。仅依靠上述轨迹压缩方法进行压缩时,由于大量停留点被压缩导致轨迹信息严重缺失。针对上述情况,本研究设计了压缩轨迹权重机制,其目的在于通过对停留点进行再次筛选,避免因为坐标信息重复或相近而导致停留点被大量删除。从而保留重要的轨迹特征信息。其具体方法如下:加入权重的轨迹压缩,是在进行FMDP算法的停留点筛选后,将出现的多个停留点连续区间视为停留点区间。在每个停留点区间,设停留点数为ns,停留时间为ts,停留阈值为β=ns/ts,对β进行向下取整为δ,那么δ为该停留点区间应保留的停留点个数。

在每个停留点区间,由于渔船长时间的停留出现多个相同的坐标点集,每个点集均是相同的坐标点所组成。设在此区间中坐标点集的个数为m,将坐标点集个数m与停留点个数δ相比较:

(1)当坐标点集个数m小于停留点个数δ时,只保留该区间的首尾停留点。

(2)当坐标点集个数m大于等于停留点个数δ时,并将停留点数目ns与δ作比,得出比值γ,保留γ倍数序号的停留点。其公式如下所示:

(5)

加入权重机制的FMDP算法(FMDP algorithm with Weight mechanism added,后文称为“FMDPW算法”)虽然提高了算法的复杂度,但处理停留时间较长的渔船作业行为更加精准;反之,处理停留时间较短的渔船作业行为时,未加入权重机制的FMDP算法更加快速准确,提高了轨迹压缩的效率,完成了对渔船不同作业类型轨迹的高效压缩。其算法流程由图3所示,图3中i代表轨迹点从队首到队尾的序号;di+1代表由经纬度坐标系转化为笛卡尔直角坐标系后的第i点与第i+1点的距离。

图3 算法流程

2 试验验证与算法对比

2.1 参数设定

为了对本研究提出的FMDP轨迹压缩方法的准确性和执行的效率进行验证。采用 Python 语言编写,选取来自大连世想海洋科技有限公司的原始试验数据集起止时间为2018年1月20日到2018年12月20日,在压缩效率方面与原始DP算法性能进行对比评估。

评估指标:以压缩效率作为试验结果参考,对FMDP与DP算法进行评测,评测公式如下所示:

(6)

式中:Cp为压缩率;Vp为剩余轨迹点数;O为原始轨迹点数。

2.2 压缩效率对比试验

对渔船作业行为进行有效监控的前提是完成渔船轨迹数据信息的高效压缩处理,如通过处理压缩轨迹中转向与停留的特征信息,可以较为准确判定渔船是否有越界、骗保等违规行为;通过数据压缩可以删除原始轨迹中冗杂、错误的轨迹点。但是由于大量数据被压缩难免出现重要轨迹点缺失的问题,例如:鱿鱼钓渔船在进行捕捞作业时长时间处于漂流状态,会产生的大量漂流轨迹点,之前轨迹压缩方法会因为数据重复将大量的停留作业轨迹点删除,导致渔船作业信息丢失。因此为了实现渔船在不同作业情况均能高效地进行轨迹压缩,本研究依据渔船轨迹估计的复杂度在算法中加入权重机制,以此实现较为完整的保留渔船轨迹的特征信息。

试验一:FMDP算法与DP算法对比相同渔船在不同日期的轨迹压缩情况,通过轨迹的压缩效果,来测试FMDP算法的压缩性能。

(1)轨迹压缩效果情况对比

在数据集中选取一组较为复杂轨迹数据,使用FMDP算法与DP算法进行压缩效果对比评估。如图4所示。通过计算FMDP算法与DP算法的轨迹压缩率Cp均超过98%,可知DP算法与FMDP算法均能实现对轨迹的有效压缩,但是通过对比压缩情况可以得出,当渔船作出停留转向等行为出现造轨迹折返时,DP算法在进行轨迹压缩时可能会删除速度变化较大的动态信息点,进而导致轨迹的时间特征的丢失[30],而FMDP算法会保留渔船转向、停留的重要特征信息(图4c中画圈处),在确保高压缩率的基础上,保留了更多的渔船轨迹的特征信息。

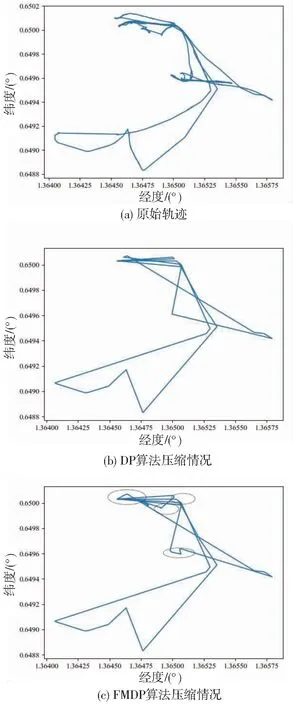
图4 12月7日轨迹压缩对比情况

(2)压缩率对比试验

为了进一步对比FMDP算法与DP算法的压缩效果,进行了压缩率的对比试验,如表1所示,DP算法的压缩率Cp均值为98.0%,FMDP的压缩率Cp均值为97.5%,最低为95.51%。虽然FMDP算法在压缩率上略低于DP算法,但依据图4得出结论,DP算法所删除的点集,大多属于转向点与停留点被删除,无法反映轨迹的时间特征。

表1 两种压缩算法的试验结果

对于轨迹的整体规划不理想。FMDP算法则是在确保压缩率Cp平均达到97.5%的基础上,保证了压缩后轨迹具备更多特征信息。此外,通过对比两种算法的轨迹压缩消耗的时间可以看出,FMDP算法处理轨迹压缩花费时间与DP算法所消耗的时间相近,可见算法处理数据的压缩时间不会对试验结果评估造成影响。

试验二:为判断在FMDP算法中加入权重机制,是否在处理所有的轨迹时都具有必要性。本试验将待压缩轨迹分为A,B两组:A组为复杂渔船轨迹;B组中为简单渔船轨迹。进行压缩效率的计算,其具体结果如表2所示。

表2 权重对压缩率影响的试验结果部分样例

通过对比表2中的A、B两组数据中的压缩率变化可以得出以下结论:FMDPW算法的压缩率虽然要低于FMDP的压缩率,但保留了原始轨迹中更多的特征信息,且原始轨迹复杂程度与保留的特征信息数量成正比。当轨迹复杂需要保留更多特征信息时,优先考虑使用FMDPW算法处理原始轨迹。为进一步证明权重机制的必要性,直观反应轨迹压缩后的变化情况。试验筛选出A、B两组中有代表性的数据进行数据可视化,其对比结果如下图5、图6所示。

图5 A组复杂轨迹压缩率对比图

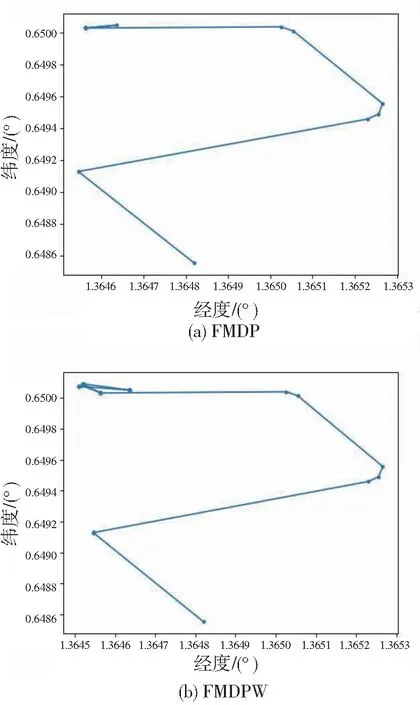
图6 B组简单轨迹压缩率对比图

通过对比图5中的数据可以看出A组数据在加入权重机制处理后,更完整地保留了原始轨迹的变化特征,可以得出结论:FMDPW算法可以有效地从船舶轨迹数据中筛选出体现原始轨迹特征的子集,保留原始轨迹的特征信息。虽然FMDPW算法保留了原始轨迹中更多的特征信息,但导致了渔船轨迹的压缩率和压缩效率降低。并且根据图6可以看出,简单的渔船轨迹在FMDPW算法压缩后轨迹并没有明显变化,因此在处理简单的渔船轨迹时,无需在算法中加入压缩权重机制。根据原始轨迹的复杂程度选择是否进行权重考虑,可以最大程度上保证轨迹压缩的高效性与准确性。

通过试验对比与压缩率对比,可以得出FMDP算法在处理渔船轨迹时能精准保留渔船的特征信息。同时FMDP算法权重机制的考虑有效避免停留点过多造成压缩轨迹失真的问题。在保证高压缩率的情况下保留轨迹特征信息。

3 结论

本研究基于原始DP算法设计了一种特征点分离的多阈值DP算法,并加入权重机制的优化研究。

本研究基于原始算法首次提出了将轨迹中的停留点进行分离处理的方法,并通过权重机制以及加入角度阈值改进算法,最大程度保留了渔船轨迹的特征信息,为后续计算捕捞鱼量,统计渔场捕捞强度提供数据支持,更能有效完成渔船作业行为分析,但渔船停留点阈值上选取需要进一步验证。后续将会研究算法的最佳距离阈值与尺度变化间的定量关系,将着重考虑阈值的影响。