宽带分裂波束探鱼仪目标方位估计方法
汤涛林,张玉涛,王志俊,尹项博,李国栋
(中国水产科学研究院渔业机械仪器研究所,上海 200092)
精确测量目标强度是利用探鱼仪估计鱼体大小和生物量的必要条件[1-2],这需要确定目标在波束空间中的位置以修正波束指向性造成的测量偏差[3]。普通探鱼仪只能估计目标距离,分裂波束探鱼仪将换能器分为4个象限,通过每个象限接收到的信号时延确定目标的方位。传统的分裂波束探鱼仪使用脉冲连续(CW)探测信号,通过接收信号相位差估计方位[4]。宽带分裂波束探鱼仪使用线性调频(LFM)信号[5],与窄带系统相比,宽带系统可以获得更丰富的频谱信息[6-7],更高的距离分辨率和更强的目标检测能力[8],但宽带信号的相位是时变的,无法通过相位差估计目标方位[9]。
常用的宽带信号方位估计方法包括互相关[10-12]、互功率谱[13-15]和自适应滤波[16-17]。这类方法都需要一个时间窗截取数据后进行计算,如果鱼群密度较高,数据窗内存在多个目标回波时,会产生较大误差[18],而缩短数据窗长度,估计性能会下降。Jung等[19]提出使用宽带信号和窄带信号结合的方式,宽带探测脉冲进行目标强度估计、距离估计、频谱估计等处理,而窄带脉冲进行目标方位估计和目标跟踪,这种方法效率太低。超分辨率算法[20-22]可以突破该限制,得到数据窗内多个目标的方位估计。但这类方法需要对相关矩阵进行子空间分解或拟合,探鱼仪的回波中包含大量目标,目前的器件性能无法满足实时计算的要求。脉冲压缩是宽带声呐、雷达常用的信号处理方法[23-24],线性调频信号是宽带探鱼仪最常用的信号形式。
本研究提出一种利用线性调频信号脉冲压缩相位实现分裂波束目标方位估计的方法,无数据窗长度限制,在目标间隔距离大于脉冲压缩后距离分辨率时可给出准确的方位估计。
1 材料与方法
1.1 分裂波束目标定位原理
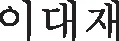
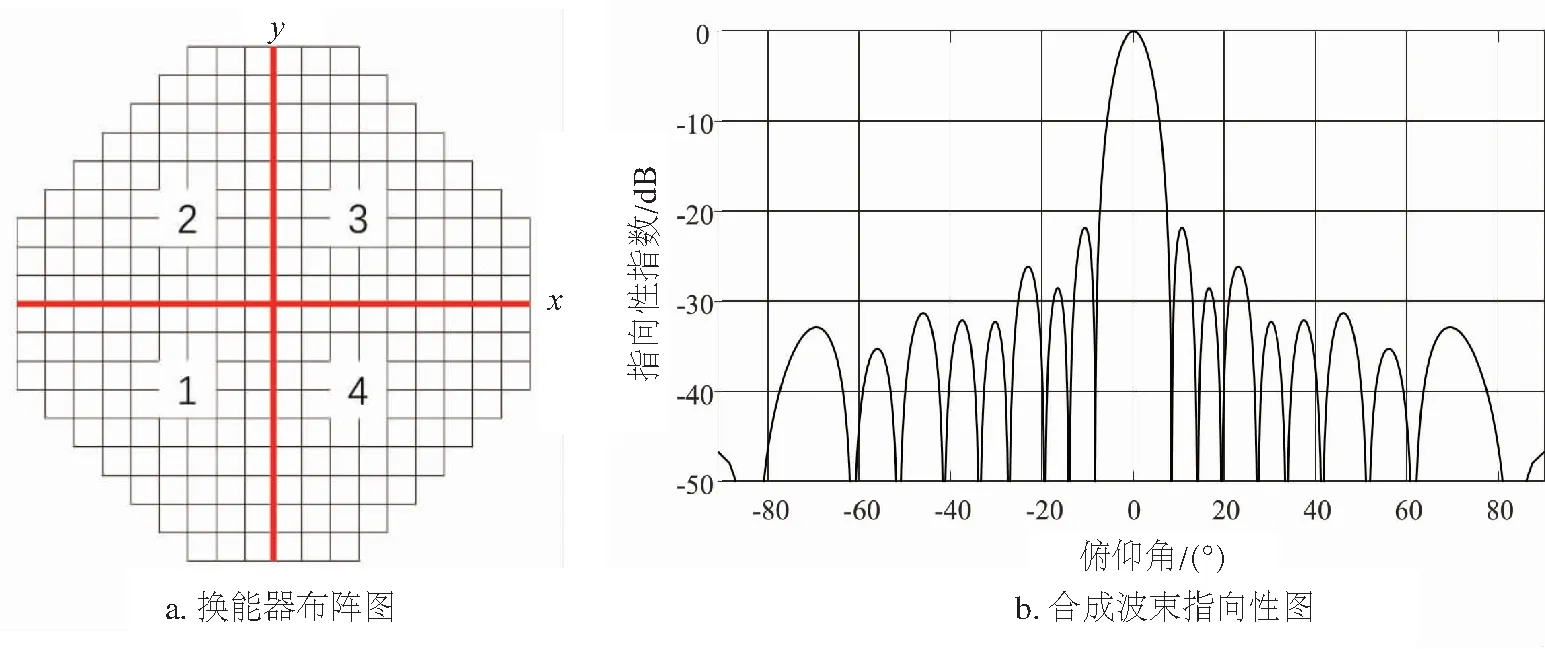
图1 分裂波束换能器
发射时4象限换能器并联发射信号,接收时换能器1、2接收信号相加获得左路信号,3、4接收信号相加获得右路信号,2、3接收信号相加获得上路信号,1、4接收信号相加获得下路信号。
如图2所示,以左路信号和右路信号为例,X方向的目标方位角和时延的关系为:

图2 两路信号的时延
(1)
式中:D为合并后左右子阵的等效声中心距离,m;τ为时延,s,两子阵接收信号来自同一目标,分别用s(t)和s(t-τ)表示;θ为信号与声轴夹角;C为声速,m/s。
估计时延即可得到目标方位[27]。同理可获得Y方向的目标方位角。
1.2 正交解调
宽带分裂波束探鱼仪使用的探测信号为:
A(t)cos(2πfct+πKt2)
(2)
式中:fc为载波频率,Hz;K为调频斜率,K=B/T;B为带宽,Hz;T为发射信号脉宽,s;

s(t)=A(t-τ)cos[2πfc(t-τ)+
πK(t-τ)2]
(3)
为了方便后续的计算,需要把接收信号变为复基带信号。由于探鱼仪的载波频率比带宽大很多,可以使用如图3所示的正交解调方法。

图3 正交解调
接收信号s(t)一路与2cos(2πfct)相乘得到:
2s(t)cos(2πfct)=2A(t-τ)cos[2πfc(t-τ)+πK(t-τ)2]cos(2πfct)=A(t-τ)
{cos[4πfct-2πfcτ+πK(t-τ)2]+cos[πK(t-τ)2-2πfcτ]}
(4)
另一路与-2sin(2πfct)相乘得到:
-2s(t)sin(2πfct)=-2A(t-τ)cos[2πfc(t-τ)+πK(t-τ)2]sin(2πfct)=A(t-τ)
{-sin[4πfct-2πfcτ+πK(t-τ)2]+sin[πK(t-τ)2-2πfcτ]}
(5)
分别经过低通滤波器LPF后,移除高频部分得到复基带信号:
z(t)=I(t)+jQ(t)=cos[πK(t-τ)2-2πfcτ]+jsin[πK(t-τ)2-2πfcτ]
=exp[jπK(t-τ)2-j2πfcτ]
(6)
1.3 脉冲压缩
探鱼仪向下探测单体目标时,忽略多普勒和多途的影响,接收信号可以看作发射信号时移和衰减后的副本。假设接收信号中的噪声是加性白噪声,此时匹配滤波器是检测信号的最优滤波[28]。对于探鱼仪的距离分辨率一般采用信号频带的主瓣宽度定义,对应了主瓣两个半功率点之间的宽度。采用该定义匹配滤波后的目标距离分辨率变为[29]:
(7)
对于宽带探鱼仪,匹配滤波后输出的信号宽度小于原回波信号宽度,因此该技术也称为脉冲压缩。匹配滤波器的时域传递函数为:
h(t)=s*(-t)
(8)
滤波器输出可以表示为:

(9)
为了消除正交解调中低通滤波器造成的相移[28]影响,匹配滤波的相关副本采用发射信号通过正交解调后的输出。
1.4 脉冲压缩后的时延估计
由(8),LFM信号的匹配滤波器为:
h(t)=s*(-t)=A(-t)exp(-jπKt2)
(10)
忽略回波的幅度衰减,由(6)和(9)得到:
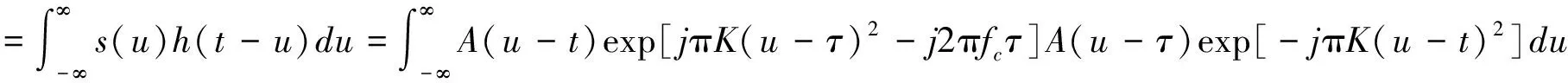

当t≥τ时,

令v=2u-τ-t;
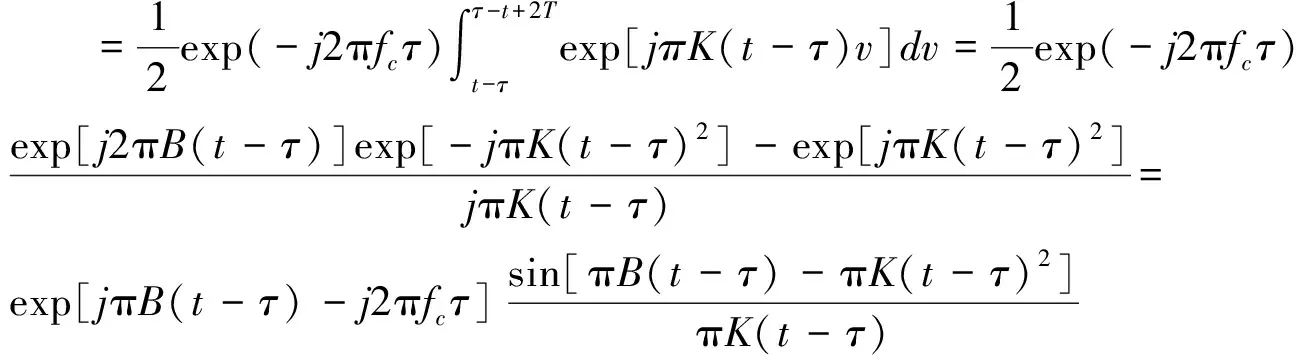
(11)
同理,当t<τ时,

(12)
以右路和左路信号为例,设同一目标到达的时延分别为τ1和τ2,匹配滤波输出分别为y1和y2,由(11)和(12)得到:
(13)
其中A1(t)和A2(t)为匹配滤波后的幅度函数,接收信号时延差的表达式为:
(14)
其中imag[r(t)]为r(t)的虚部,real[r(t)]为r(t)的实部。由式(1)可得到X方向的目标方位角。同理,由上下两路计算即可得到Y方向的目标方位角。
2 结果与分析
为了验证算法有效性,采用以下仿真模型:LFM信号载波频率170 kHz;带宽60 kHz;发射脉宽1.024 ms;采样频率2 MHz;水中声速1 500 m/s;分裂波束子阵等效声中心距离27.5 mm;在距离换能器10 m和10.012 5 m处各有一目标,其X轴方向方位角分别为5°和-5°。其回波如图4所示,此时两个信号重叠,无法区分。

图4 换能器接收回波信号
脉冲压缩和方位角估计结果如图5所示。脉冲压缩后出现两个幅度峰值,分别出现在9.999 m和10.013 6 m位置,与设定目标的距离分辨误差为-0.001 m和0.011 m。对应的角度估计值分别为4.923°和-5.023°,角度估计误差分别为-0.077°和-0.023°。由(7)可知带宽60 kHz时探鱼仪的距离分辨率为0.012 5 m,该仿真结果表明在目标间距接近距离分辨率极限时,算法仍然可以获得较为准确的估计。

图5 脉冲压缩输出和X轴方向方位角估计
为了验证被高斯白噪声影响时算法的抗噪声能力,采用以下仿真模型:距离换能器10 m处设置一个目标,令入射角为3°,其他参数同上,分别使用脉冲压缩相位和互谱法[14]在不同信噪比下各进行1 000次角度估计,再令入射角为6°,重复以上计算,角度估计标准差和信噪比关系如图6所示。

图6 不同信噪比下角度估计标准差

3 结论
研究了宽带分裂波束探鱼仪目标定位问题,提出一种利用脉冲压缩相位进行目标方位估计的方法。该方法在回波中存在多个目标,且目标间距接近距离分辨率极限时,仍然可以获得较为准确的方位估计。比较了脉冲压缩相位法和互谱法的方位估计性能。仿真显示,信噪比6 dB以上时,脉冲压缩相位法和互谱法具有相当的估计精度,低信噪比时,脉冲压缩相位法具有更高精度。由于相位卷绕,脉冲压缩相位法对目标的方位角范围有限制,超出该范围的方位角无法准确估计。该问题可通过限制换能器波束开角或增加解相位卷绕算法解决。脉冲压缩相位法对脉冲压缩后的结果进行一次相位角计算就可获得结果,计算资源耗费少,易于工程实现,具有很高的实用性。

