滩涂贝类采捕机路径跟踪控制仿真分析

王玉瑞,张国琛,2,3,张寒冰,2,3,李秀辰,2,3,张 倩,2,3,李航企,刘法伟,陈鸿宇,母 刚,2,3

(1大连海洋大学机械与动力工程学院,辽宁 大连 116023;2 辽宁省海洋渔业装备专业技术创新中心,辽宁 大连116023;3 设施渔业教育部重点实验室,辽宁 大连116023)

中国作为贝类养殖大国,不仅贝类养殖种类繁多,且产量居于世界前列[1-3]。采捕作为滩涂贝类养殖的主要环节,高效环保的采捕技术与设备是保障滩涂贝类养殖产业可持续发展的先决条件[4]。但当前中国滩涂贝类采捕机智能化程度低,采捕路径无法精准控制,漏采和复采问题突出,直接影响采捕效率和产量[5-7],为提升滩涂贝类精准采捕水平,采捕机路径跟踪控制技术研究十分迫切。

国内外学者对农田作业设备路径跟踪控制技术做了众多研究[8-11],取得了一定进展。根据研究对象转向特性不同,分为基于阿尔曼转向的轮式行走机构和基于差速转向的履带式行走机构[12-15]。对于轮式行走机构,Bevly等[16]采用线性二次控制器进行作业路线纠偏控制,控制器将横向偏差修正在0.3 m以内,但算法结构复杂、计算步骤烦琐,对硬件结构具有较高要求,导致成本大幅增加。针对履带式行走机构,Zhang等[17]基于最小单值段同化核角对履带机器人进行模糊控制,通过改变机器人初始时刻位置参数,验证模糊控制器的可行性,但采用视觉导航技术,存在受光照环境影响大、路径提取效率低等问题,难以适应带水滩涂等作业环境。张朝宇等[18]为小型履带式播种设备设计了一种模糊自适应纯追踪控制器,经田间试验证明该控制器具有路径跟踪偏差小、上线快等优点,但存在成本高、转向执行机构复杂,系统维护不便等问题。综上所述,当前路径跟踪控制技术研究主要围绕田间作业设备进行,针对渔业装备路径跟踪控制技术鲜有报道。

因此,针对滩涂贝类采捕机路径跟踪控制技术需求,本研究以滩涂贝类养殖区域为试验场地,通过对采捕机控制系统参数进行标定,建立滩涂贝类采捕机运动学模型,设计一套带修正因子的模糊控制系统,并利用Matlab/Simulink仿真验证控制系统效果,以期为滩涂贝类采捕机路径跟踪提供参考。

1 滩涂贝类采捕机转向运动理论分析

1.1 制动转向运动学建模

围绕自主设计研发的履带式滩涂贝类采捕机展开研究,进行路径跟踪控制系统研究。采捕机采用单边制动形式进行转向。因滩涂作业环境恶劣[19-21],为满足采捕机正常作业需求,需要控制器在较低速度下稳定运行,且要求系统的整体结构简单,便于维护。

滩涂贝类采捕机如图1a所示,主副卫星定位天线间距1.5 m(深圳市北天通讯有限公司BT-641B型RTK GNSS)与采捕机纵轴重合,以副天线在前、主天线在后的排列方式安装在采捕机车顶,用于采捕机姿态位置等参数测量,转速传感器(欧姆龙E6B2-CWZ6C)通过联轴器与采捕机两侧履带驱动轮相连。图1b为采捕机转向机构电控方案,用电控转向操纵杆替代手动转向操纵杆机构实现电控操纵功能,取代人工完成采捕机单边制动转向操作。

图1 滩涂贝类采捕机及转向机构传动示意图

由于滩涂贝类采捕机行驶速度较低,故忽略侧倾、俯仰、横摆等因素对采捕机运动控制的影响[22-24],如图2所示为高斯克吕格投影[25-27]坐标系下滩涂贝类采捕机运动框图。

图2 滩涂贝类采捕机平面运动

图示可得:

(1)

其中:

(2)

式中:Vm为采捕机纵轴中心处行驶速度,m/s;VL为左侧履带行驶速度,m/s;VR为右侧履带行驶速度,m/s;r为两侧履带驱动轮半径,m;nL、nR分别为采捕机左右两侧履带驱动轮转速,r/min。

采捕机转向角速度为:

(3)

式中:H为采捕机履带中心距,m。

采捕机制动转向运动学模型为:

(4)

由采捕机制动转向运动学模型可知当VL=VR时,采捕机沿直线路径进行作业,当VL=0,即左侧履带停转时,右侧履带保持原有运动速度,滩涂贝类采捕机向左转向,反之,向右转向。

1.2 轨迹误差模型

为满足滩涂贝类采捕机直线作业路径跟踪需求[28-29],需将卫星定位天线采集到的经纬度等参数转为高斯克吕格投影坐标系下平面坐标,并计算相对于目标导航路径的误差值,从而进行路径纠偏操作。

在高斯克吕格投影坐标系下,通过预设起点A(x1,y1)和终点B(x2,y2),得目标导航路径方程为:

(y2-y1)X+(x1-x2)Y+y1x2-y2x1=0

(5)

令采捕机实时变化的位置坐标信息为(XS,YS),由式(6)可得采捕机相对于目标导航路径横向偏差(L):

(6)

其中:

(7)

设目标导航路径的航向角为θ,设定XW轴正方向为航向角零度基准线,以逆时针旋转方向为正,取值范围为0～360°,式(8)可确定目标导航路径目标航向角为:

(8)

目标导航路径的目标航向角与采捕机运动航向角之间的夹角作为航向偏差,式(9)得航向偏差(θe)为:

θe=θ-θS

(9)

式中:θS为采捕机运动航向角,(°)。

由式(9)可知,采捕机前进航向角在目标导航路径航向角逆时针方位时,航向偏差为小于零。反之,航向偏差为大于零。

2 路径跟踪控制系统设计

2.1 控制参数标定

为保证仿真结果的准确性,首先对控制系统中基本参数(两侧履带驱动轮转速、采捕机转向角)进行标定,试验在辽宁省锦州凌海贝类养殖滩涂(北纬40°51′1″,东经121°28′33″)进行。试验设备除采捕机外还包括PC机、BT-641B型卫星定位设备、欧姆龙E6B2-CWZ6C型转速传感器等。

标定方法:①待海水退潮时,选离岸约300 m的滩涂区域作为试验场地,令滩涂表面海水深度5 cm及以下为干滩,反之为湿滩。②将转速传感器接入PC机端口,在设计的软件界面中,分配转速传感器串口号,设波特率为9 600 bps。③调整采捕机行驶速度,将油门与档位固定后通过软件记录采捕机在不同工况(干滩、湿滩)60 s内两侧履带驱动轮转速。④在干滩区域,断开转速传感器,将BT-641B型卫星定位设备通过串口与PC机连接。⑤在Compass Receiver Utility软件中设置数据传输波特率为115 200 bps,采样频率为10 Hz,高度截止角为10°,输入“Log com1 gpgga ontime 1”“Log headinga ontime 1”等指令,对#HeadingA报文进行记录。⑥将获取的报文信息在Matlab中完成航向角数据解析,取相邻航向角差值作为采捕机转向角范围。

履带驱动轮转速标定结果如表1所示,并联立式(1)(2)可计算采捕机在干滩作业理论纵向行驶线速度,速度区间为0.018～0.022 m/s,实测纵向行驶线速度区间为0.017～0.020 m/s,二者相对误差在10%内,产生的主要原因是采捕机行驶过程中存在履带滑转现象,因误差较小,履带驱动轮转速标定结果与实际采捕机工作转速基本一致,证明实测转速可作为控制系统参数需求。并取采捕机在干滩作业理论纵向行驶速度为0.02 m/s;而采捕机在湿滩作业时理论和实际纵向行驶线速度最大相对误差为6.25%,取采捕机纵向行驶线速度为0.03 m/s。

由表2可知,采捕机在干滩作业左转相邻航向角差值为2.87°～3.55°,实际转向角范围2.71°～3.44°,右转航向角差值区间为2.68°～3.62°,实际值在2.46°～3.40°之间,采捕机左右转向时,航向角差值均小于实际测量值,造成这一偏差主要原因是采捕机履带转向时存在转向阻力,但相对误差小于8.2%,因此可将航向角差值作为采捕机转向角阈值,将其作为控制转向角基本论域,并取采捕机最大转向角为3°。

2.2 路径跟踪控制器结构设计

如图3所示为滩涂贝类采捕机路径跟踪控制框图,采用二输入一输出结构形式。为保证控制系统平滑性,以采捕机相对于目标导航路径横向和航向角偏差为带修正因子的模糊控制系统的输入参数,经过控制系统的模糊化、模糊规则梳理、清晰化处理后输出滩涂贝类采捕机转向角(α)。

图3 滩涂贝类采捕机路径跟踪控制框图

2.3 常规模糊规则设计

2.3.1 输入输出参数隶属度函数

设定输入控制器的横向偏差基本物理论域(Lb)为{-1 m,1 m},模糊化等级(NL)为[-6,6],航向偏差基本物理论域(θeb)为{-30°,30°},模糊化等级(Ne)为[-6,6],控制器输出的控制转向角基本物理论域(αb)为{-3°,3°},模糊化等级(Nα)为[-6,6],输入输出参数均划分{负大,负中,负小,零,正小,正中,正大}7个模糊级别,用{NB,NM,NS,ZE,PS,PM,PB}表示。由式(10)可分别求出横向偏差(L)、航向偏差(θe)的量化因子KL、Kθ以及控制转向角(α)的比例因子Kα。

(10)

2.3.2 路径跟踪系统模糊控制规则

模糊控制规则基于人们实际生活中对事物规律不断进行探索总结的经验[30-31]。如图4所示为滩涂贝类采捕机在作业过程中可能出现的位置偏差情况。根据不同的偏差状态建立对应的模糊控制规则,从而达到精准控制采捕机路径跟踪。

图4 滩涂贝类采捕机相对目标导航路径位置

当滩涂贝类采捕机的横向偏差较大时,要求控制系统输出转向角为较大值,以快速纠正横向偏差值,而当滩涂贝类采捕机横向偏差收敛到一定阈值时,为了避免超调量的出现,应减小控制系统输出转向角,以保证滩涂贝类采捕机路径跟踪控制系统的稳定性。此外,由于采捕机电控推杆采用开关量控制,且采捕执行机构入土工作,因此在确保采捕机路径跟踪精度的基础上,避免过于频繁的转向控制产生振荡或者对采捕机机械部件造成破坏,通过修改模糊控制规则,将路径跟踪稳态区间设置在一阈值范围内。

由上述分析获得的滩涂贝类采捕机路径跟踪模糊控制规则如表3所示。

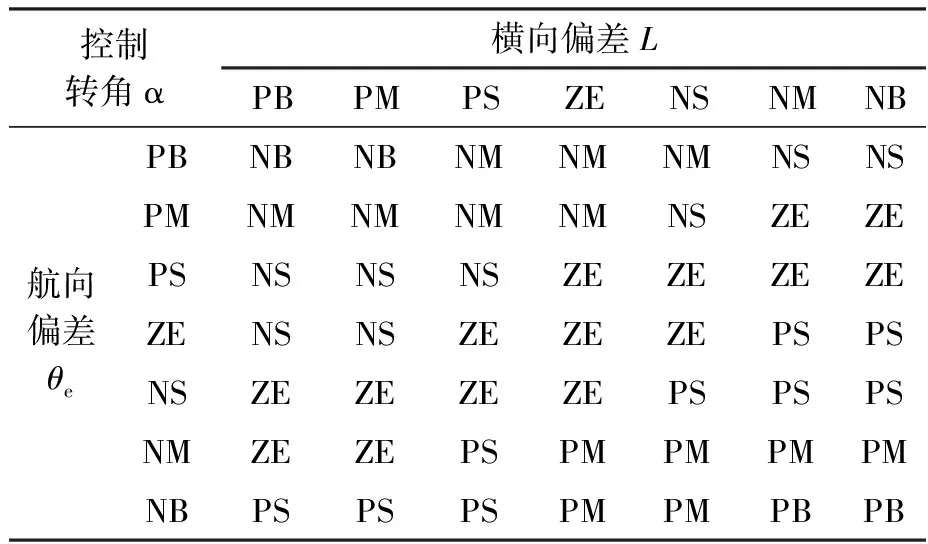
表3 滩涂贝类采捕机模糊控制规则

2.4 带修正因子的模糊控制系统设计

为了更好地达到采捕机路径跟踪控制目的,提高算法的环境适用性,在常规模糊控制器基础上增加了一种带修正因子的模糊控制系统,不断进行模糊控制规则的调整,对采捕机转向角参数值修正,带修正因子的控制规则表达可用式(11)表示。以下为一维控制结构形式的修正因子(λ)控制系统设计过程。

(1)输入输出变量模糊化

如表4所示为修正因子控制系统参数表,以基本模糊控制器的横向偏差为输入,修正因子(λ)作输出。采用一维控制结构形式。与常规模糊控制系统设计不同的是,在修正因子控制系统中,将输入的横向偏差隶属度用正态分布的隶属函数求解,其模糊级别仍用{NB,NM,NS,ZE,PS,PM,PB}来表示,控制系统的输出λ模糊级别划分为4个,即:{ZE,PS,PM,PB}。

表4 修正因子控制系统输入输出参数

U=[λL+(1-λ)θe] (0<λ<1)

(11)

式中:[ ]代表取整符号;λ为修正因子。

(2)修正因子控制规则的建立

本研究主要对采捕机横向偏差进行调节,因此,当横向偏差较大时需要输出较大转向角进行快速路径纠偏操作,而当横向偏差较小时,为防止超调的出现,此时,应减少转向角的参数值,以保证控制的平滑性,基于这一原则,制定的控制规则如表5所示。

表5 修正因子控制规则

3 仿真结果与分析

3.1 系统仿真模型

在控制参数标定基础上,对滩涂贝类采捕机带修正因子的模糊控制系统进行不同作业速度下的仿真控制效果验证,在Matlab/Simulink中搭建了如图5所示的采捕机路径跟踪控制系统仿真模型。

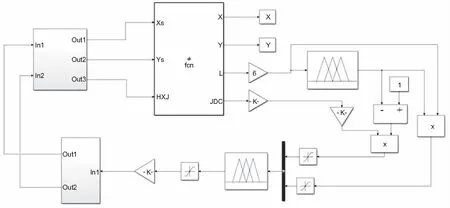
图5 带修正因子的模糊控制仿真模型

设定滩涂贝类采捕机初始时刻位姿为(1 m,0 m)、航向角为60°,目标导航路径为Y=X。在采捕机初始速度(v)分别为0.02 m/s(干滩作业)、0.03 m/s(湿滩作业)时,以相同的位姿和目标导航路径参数进行仿真试验,设定带修正因子的模糊控制系统采样时间为2 s,仿真时间为1 000 s。

3.2 仿真结果分析

如图6、图7所示为带修正因子的模糊控制系统仿真控制效果。由图6a、图7a可知相较于常规模糊控制系统,带修正因子的模糊控制系统可进行横向和航向偏差分段调节,首先将横向偏差进行误差修正,后为防止超调量出现,实际行驶路径曲率不断变小,并回归至目标导航路径。由图6b、图7b可知,当采捕机作业速度为0.02 m/s时,带修正因子的模糊控制系统在时间(Time)为500 s时将横向偏差阈值收敛至0.03 m内,较常规模糊控制系统缩短了400 s,减少了约44.44%,采捕机作业速度为0.03 m/s时,带修正因子的模糊控制系统在时间为360 s时将横向偏差阈值收敛至0.03 m内,较常规模糊控制系统缩短了200 s,减少了约35.71%。

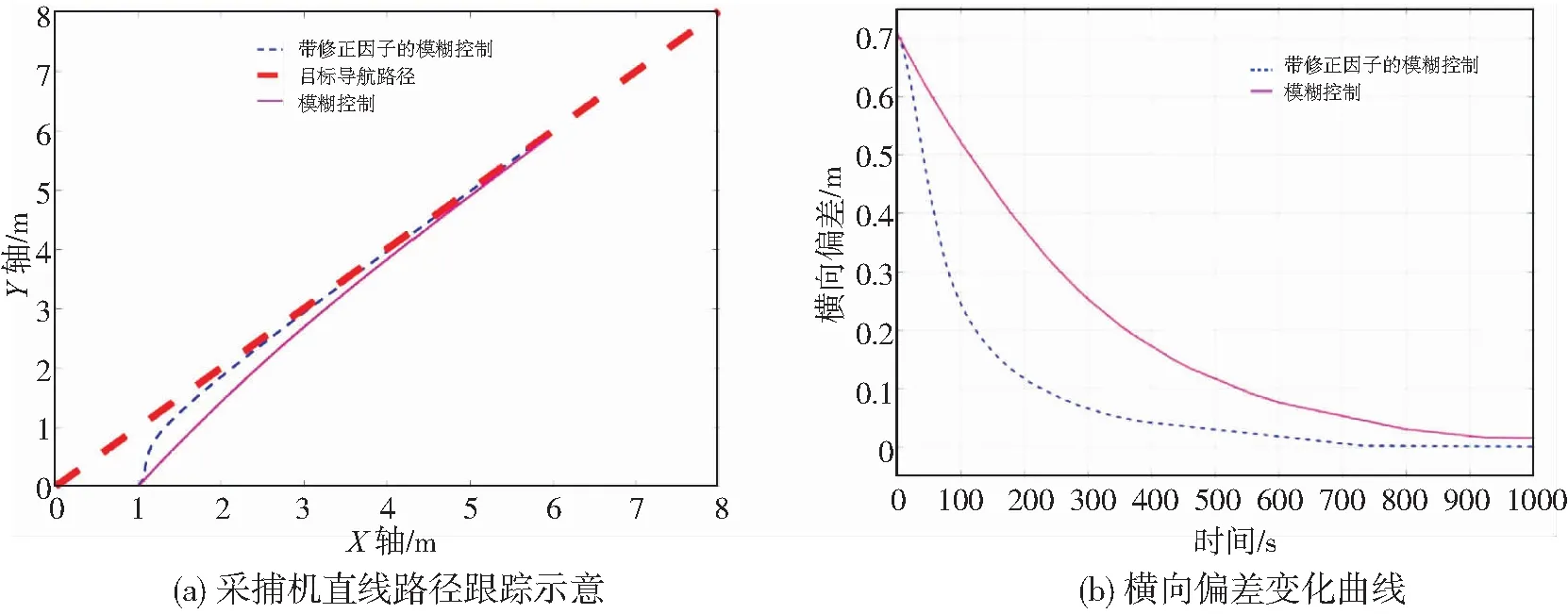
图6 采捕机速度为0.02 m/s时带修正因子的模糊控制效果

图7 采捕机速度为0.03 m/s时带修正因子的模糊控制效果

此外,带修正因子的模糊控制系统在采捕机不同行驶速度(0.02 m/s、0.03 m/s)下,均能将横向误差稳态阈值收敛在0.02 m区间以内,相较于常规模糊控制具有稳态误差小、控制精度高等优点。表6为采捕机在不同控制器下的路径跟踪横向偏差稳态阈值,设定

表6 路径跟踪横向偏差稳态阈值

(12)

式中:ξ代表路径跟踪精度百分比(符号正负代表路径跟踪精度增加或降低,其值为正数,表示路径跟踪精度增加,为负,代表路径跟踪精度下降);L为常规模糊控制器横向偏差稳态阈值,m;L′为带修正因子的模糊控制器横向偏差稳态阈值,m。

由表4得带修正因子的模糊控制系统相较于常规模糊控制,导航精度分别提升了2/3、1/3。

此外,为研究带修正因子的模糊控制系统抗干扰能力,设定采捕机初始时刻位姿姿态为(0.5 m,0 m)、航向角为60°。在800 s时,给予系统一时长30 s、幅值30°的干扰,结果如图8所示。

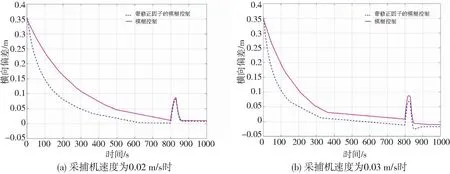
图8 带修正因子的模糊控制系统抗干扰仿真效果

由图8a可知,当采捕机行驶速度为0.02 m/s时,带修正因子的模糊控制系统最大横向偏差为0.08 m,较常规模糊控制器减小了11.11%,在时间为858 s时将横向偏差收敛至0.02 m以内,较常规模糊控制器调节时间减小了20%,由图8b可知,当采捕机行驶速度为0.03 m/s时,带修正因子的模糊控制系统最大横向偏差为0.05 m,较常规模糊控制器减小了37.5%,在时间为896 s时将横向偏差收敛至0.02 m以内,较常规模糊控制器调节时间减小了47.2%,通过仿真表明带修正因子的模糊控制系统具有抗干扰能力强、调节时间短等优点。

本研究中带修正因子的模糊控制系统相较于甘鑫等[10]设计的纯追踪算法的控制系统,不仅避免了因目标点选取不当造成控制系统振荡或调节时间过长问题,且对车速、滑移等因素不敏感,带修正因子的模糊控制系统是基于当前采捕机位置姿态参数进行误差纠偏操作,不需要纵向车速匹配。此外,通过修正因子的作用,保证了控制系统的平滑性。与张朝宇等[18]基于阀控液压马达和电液比例阀的电控转向机构相比,本研究采用锁止装置对采捕机进行电控转向系统改造,设计方案简便、装置成本低且可实现手动/自动切换。

4 结论

本研究以自主设计研发的履带式滩涂贝类采捕机为研究对象,设计了一套带修正因子的模糊控制系统。基于实际滩涂环境对控制参数的标定结果,仿真验证了采捕机行驶速度分别为0.02 m/s、0.03 m/s时,带修正因子的模糊控制系统较常规模糊控制系统导航精度提升了2/3、1/3。在受到外界干扰时,带修正因子的模糊控制系统较常规模糊控制系统最大横向偏差分别减小了11.11%、37.5%,证明了带修正因子的模糊控制系统具有较高的控制精度和良好的抗干扰能力。