多需求点间车辆调度模型及优化算法混合求解研究

王素欣 ，熊珺恺 ，王雷震 ，，卢福强 ，温恒 ，司马聪

（1.东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004；2.东北大学 信息科学与工程学院，辽宁 沈阳 110819；3.燕山大学 经济管理学院，河北 秦皇岛 066004；4.吉林大学 计算机科学与技术学院，吉林 长春 130012）

随着经济的发展，人们对多需求点间的物流配送有更高要求，提出同时集送货的多对多的车辆调度问题（many-to-many vehicle routing problem with simultaneous pickup and delivery，M-M-VRPSPD）.

国内外多需求点间货物配送及其延伸问题的研究现状如下.

1）多对多物流问题中，Lim 等［1］提出用于研究多车型、多仓库车辆路径模型；Zhang 等［2］通过节点处重新分配模式解决多商品多车型路径问题；Hornstra 等［3-5］研究货物装箱或自然灾害背景下的多需求点问题.

2）综合集送货问题中，Berahhou 等［6］研究同时集送货的动态车辆路径问题；范厚明等［7］构建集货需求随机的两阶段模型；Dehghan 等［8-10］考虑外界干扰风险、车辆超载的交叉取送货问题.

3）需求可拆分问题中，Abdi 等［11-12］针对绿色供应链效率和特殊商品的兼容等约束提出需求拆分、分批送货模式；Bortfeldt 等［13］针对需求强制与选择拆分两种情况，建立三维装箱路径优化模型.

4）算法研究中，Wang 等［14］提出两阶段混合算法；Avci 等［15-16］利用短期禁忌表来扩大算法的搜索范围；Bolanos 等［17］提出重组方法和变异算子提高遗传算法能力.

当前研究中，多需求点间配送、同时取货送货、需求可拆分、需求可转运、多车型这5 个子问题没被考虑.现有研究存在如下问题.

1）车辆调度模式单一.一次工作中车辆仅取货或送货，装载量利用率低.

2）模型普适性差.没有考虑节点间不同货物对流约束、节点多次访问约束.

3）转运点为固定节点.转运点的数量、位置固定，全局寻优能力差，最优解为局部最优解.

4）混合算法局部优化.混合算法间无参数变量的直接联系，子算法分别优化子问题，局部最优间结合不等于全局最优.

针对当前研究不足，为扩大算法迭代范围、加快收敛速度，在Abualigah 等［18］提出的算术优化算法（arithmetic optimization algorithm，AOA）上增加概率系数、算子位置更新公式，提出改进的算术优化算法（improved arithmetic optimization algorithm，IAOA）.在Dorigo 等［19］提出的蚁群算法（ant colony optimization，ACO）上增加动态禁忌矩阵，提出改进的蚁群算法（improved ant colony optimization，IACO）.

通过优化算法混合求解方式，提出双算法嵌套优化模式，利用外层算法获得车辆配送任务，利用内层算法获得车辆路径.对比了改进的算术-蚁群混合求解（improved arithmetic optimization algorithmimproved ant colony optimization，IAOA-IACO）与算术-蚁群混合求解（arithmetic optimization algorithmant colony optimization，AOA-ACO），也对比了根据鲸鱼优化算法［20］（whale optimization algorithm，WOA）提出的鲸鱼-蚁群混合求解（whale optimization algorithm-ant colony optimization，WOA-ACO）与鲸鱼-鲸鱼混合求解（whale optimization algorithmwhale optimization algorithm，WOA-WOA），这些对比说明利用改进后的算法解决本文问题时效果最佳.

1 构建车辆调度模型

1.1 问题描述

本文解决多需求点间配送问题的描述如下：节点间有配送需求，有多车型车辆在节点间进行同时集送货服务.

节点和货物流通特征如图1 所示，箭头流通方向代表货物的流通方向，节点间的特点如下.

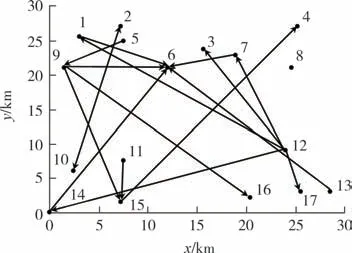
图1 货物相关节点和流通方向Fig.1 Cargo related nodes and flow direction

1）仅有货物流入或流出.如节点6、节点5.

2）同时存在货物流出、流入.如节点9.

3）货物对流.如节点2与节点10间.

4）无货物流入、流出.如节点8.

1.2 考虑需求拆分和转运的同时集送货的多需求点问题模型

1.2.1 问题假设

建立如下的假设：1）随机拆分车辆空载装载时超载的货物；2）货物可转运，为简化运算设定货物最多转运一次.

1.2.2 模型符号说明

模型符号及其说明如表1所示.

表1 模型符号及其说明Tab.1 Model symbols and description

1.2.3 数学模型

数学模型如下：

式（1）～式（5）是目标函数和基本车辆调度模型.式（1）为目标函数，表示车辆总行驶的路径最短；式（2）表示车辆不超载；式（3）表示节点间的集送货需求均被满足；式（4）体现车辆访问节点前后货物装卸过程的装载量变化；式（5）根据节点的总需求量和车辆的最大装载量选择合理的可使用车辆数量范围.

式（6）～式（10）是体现需求拆分和转运的同时集送货问题特征约束.式（6）表示车辆一次服务节点时配送量不大于节点需求，即货物可拆分；式（7）表示仅有部分车辆被使用；式（8）表示货物可转运；式（9）表示每位客户可多次访问；式（10）表示车辆配送过程中当前配送过的货物总量可大于车辆最大装载量.

模型的特点如下.

1）转运点的随机性.与固定转运点不同，根据当前货物信息随机选择转运节点以全局寻优.此特点由式（8）体现.

2）货物流通的多样性.节点间、节点与车辆间为多对多关系，与一般调度模型相比，增加了节点间不同货物的对流约束、单个或多个车辆多次访问节点的约束，增强模型普适性.此特点由式（9）体现.

3）车辆运输的高效率性.车辆在节点处有集货、送货和同时集送货模式.货物随时装卸使车辆配送的总货物量可大于车辆最大装载量，充分利用车辆装载量.此特点由式（10）体现.

2 算术-蚁群混合求解车辆调度模型

2.1 算术优化算法求解货物分配问题

2.1.1 编码产生车辆调度方案

为解决多需求点间车辆调度的编码复杂问题，提出构建虚拟需求和设定AOA 编码方式辅助算法产生调度方案.

1）虚拟需求的提出.车辆空载时节点需求超载时，随机拆分需求满足配送车辆不超载.节点的需求流通有3 种情况：①仅流入；②仅流出；③既流入又流出.在有流出需求的节点处构建虚拟需求，解决拆分后的多个需求有相同起点和终点问题.

如图2（a）所示，节点仅有单个流出需求时，虚拟需求个数与需求拆分份数相等，即需求qij拆分M份时生成M个虚拟需求.如图2（b）所示，节点有多个流出需求时，生成虚拟需求个数与多个拆分需求份数和不需拆分需求份数之和相等.每个虚拟需求的起点和终点与拆分前相同，即需求的起点和终点与拆分前相同，分别为节点i和节点u.

图2 虚拟需求Fig.2 Virtual demand

图3 AOA编码方式Fig.3 AOA encoding mode

2）AOA 编码方式.AOA 的每个初始解为三行多列矩阵，矩阵列数为拆分后的需求总数.矩阵的每行分别为转运点、转运前车辆、转运后车辆，矩阵的列表示拆分后的配送任务.

2.1.2 算术优化算法的更新迭代

AOA更新迭代求解有3个阶段.

1）通过加速函数选择迭代策略.若函数M小于0 到1 之间的随机数r1，则全局探索；否则选择局部开发.

加速函数为

式中：t为当前迭代次数；M1为加速函数当前最小值；M2为加速函数当前最大值；T为最大迭代次数.

2）利用乘除法运算特点进行解的探索，其位置更新公式为

式中：Xb(t)为当前迭代目标函数最大值；P为数学优化器概率；ξ为极小值；UB为搜索值域的上限；LB为搜索值域的下限；μ为控制参数；α为敏感参数.

3）利用加减法运算进行解的开发，其位置更新公式为

利用AOA 解决问题时，其乘法、除法算子的高分散性特点赋予算法寻优范围，加法、减法算子的精确性特点赋予算法寻优精度.但由于乘除加减算子位置更新公式的参数设定使得每次搜索迭代时，部分区域不在算法的搜索范围内，勘探范围不全面导致了算法搜索效率低，易陷入局部最优.

2.1.3 算术优化算法迭代策略的改进

针对2.1.2 总结的AOA 不足之处提出改进策略以达到扩大勘探范围的效果.改进原则如下.

1）对称原则扩大解的搜索范围.通过增加0到1之间的概率系数r4～r7，参考当前最优解位置并利用对称原则增加乘除加减算子的选择空间，解决原始AOA部分区域不在算法搜索范围内的问题.

2）二等分原则选择搜索空间.利用概率系数r4～r7对搜索空间概率二等分，保证当前算子的搜索空间与其对称搜索空间的选择概率相同.

乘法运算的位置更新公式改进为

除法运算的位置更新公式改进为

加法运算的位置更新公式改进为

减法运算的位置更新公式改进为

乘法算子以当前最优解为基准，根据式（15）进行左右对称运算，使获得的结果更分散，保证算法前期的充分搜索.同理，除法算子以式（16）进行左右对称运算.加法算子以当前迭代最优解为基准，根据式（17）进行上下对称运算，保证算法后期的局部优化精度.同理，减法算子以式（18）进行上下对称运算，扩大搜索空间，某次迭代AOA 的加减乘除算子的位置更新范围见图4（a）［21］，IAOA 相关算子的位置更新范围见图4（b）.

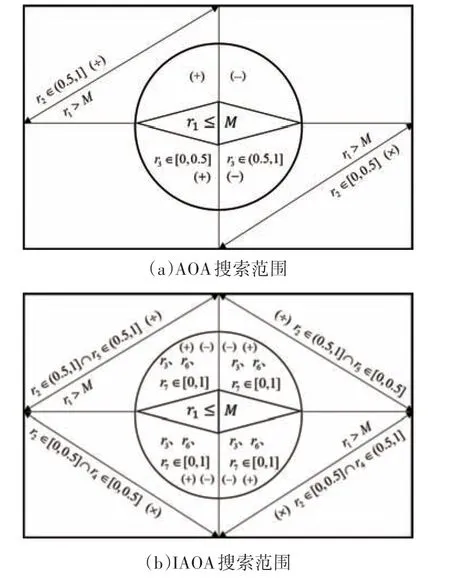
图4 AOA与IAOA搜索范围Fig.4 The search scope of AOA and IAOA

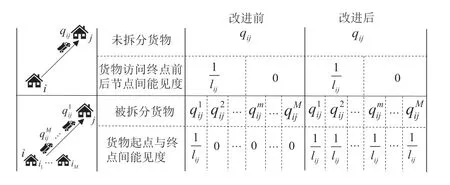
图5 ACO改进前后需求能见度变化Fig.5 Change in demand visibility before and after ACO improvement

2.2 蚁群算法求解路径优化问题

2.2.1 蚁群算法节点能见度策略的改进

利用ACO 解决TSP 问题时，节点访问一次后变为禁止访问状态.所以解决本文节点多次访问问题时，能见度矩阵失去指导车辆选择可服务节点的作用，导致算法陷入局部最优而多次无效求解，计算效率低.

动态禁忌矩阵代替能见度矩阵可解决上述问题，指导算法进入高效的搜索空间.当车辆处于当前节点时，将其剩余装载量与未配送的需求整合，利用满足装载条件的需求的起点、终点以及转运点更新当前禁忌矩阵.将不满足装载条件的需求的相关节点的禁忌值设定为0，满足条件的节点的禁忌值计算公式为

2.2.2 蚁群算法求解路径

IACO求解路径有两个阶段.

1）针对每辆配送车辆，都有k只蚂蚁随机选择节点出发，每只蚂蚁在节点i有两种选择：装载货物的终点或满足剩余装载量的货物起点.节点j的概率为

式中：τij为节点i与节点j之间的信息素浓度；υ与ω表示期望启发因子；αk表示满足访问条件的节点集合.

2）蚂蚁由节点i到节点j过程中，节点i的信息素浓度会挥发进而减少，节点j的信息素浓度会增加，信息素浓度表达式为

式中：R为信息素浓度挥发系数；Δτij表示从节点i到节点j的信息素增加量；W表示信息素量；Lk表示蚂蚁k的行驶路径长度.

IACO 中多只蚂蚁利用配送货物的起始点集合随机选择不同节点出发，每选择下一经过节点时，利用式（19）更新当前禁忌矩阵获得节点的能见度，利用式（21）、式（22）更新当前信息素浓度，同时利用式（20）更新不同节点的选择概率选择下一节点直至获得最优路径.

2.3 算法混合求解的优化思路与编码方式

IAOA-IACO混合求解的优化与编码思路如下.

1）利用IAOA 获得需求的拆分情况与车辆的配送任务.种群内个体编码方式如图3 所示，通过三行多列矩阵，整合每辆配送车辆的配送矩阵.

2）配送车辆路径的优化.IACO的输入为上述1）中配送矩阵，利用IACO进行路径优化.

3）对模型混合求解.IAOA-IACO 混合求解的流程见图6，通过双层算法嵌套优化的方式全局寻优得到最优解.混合算法外层IAOA 根据内层算法IACO的反馈更新迭代，通过双算法整体大循环模式、局部小循环模式得到全局最优解.

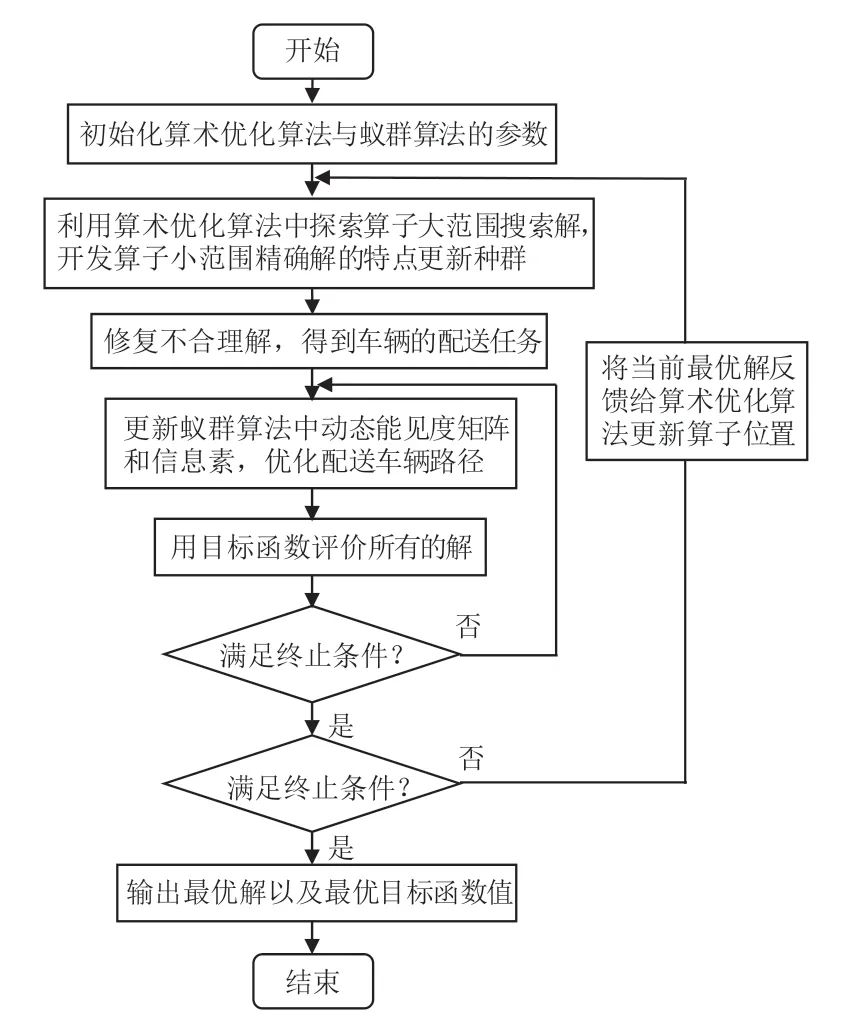
图6 IAOA-IACO混合求解流程Fig.6 IAOA-IACO hybrid solution process

3 实验仿真与结果分析

3.1 多需求点间车辆调度实验仿真

3.1.1 案例说明

目前没有M-M-VRPSPD 问题的标准案例，故本文考虑具有不同需求流向特点的节点生成测试案例.有装载量为3 t 和3.5 t 的车辆可供选择，需求流向及其关系见图1，节点坐标见表2，选择17 个客户点为例进行分析求解，其需求的起点、终点以及需求量见表3，如q(1)(6)表示货物起点、终点分别为地点1与地点6.

表2 客户节点信息Tab.2 Customer node information

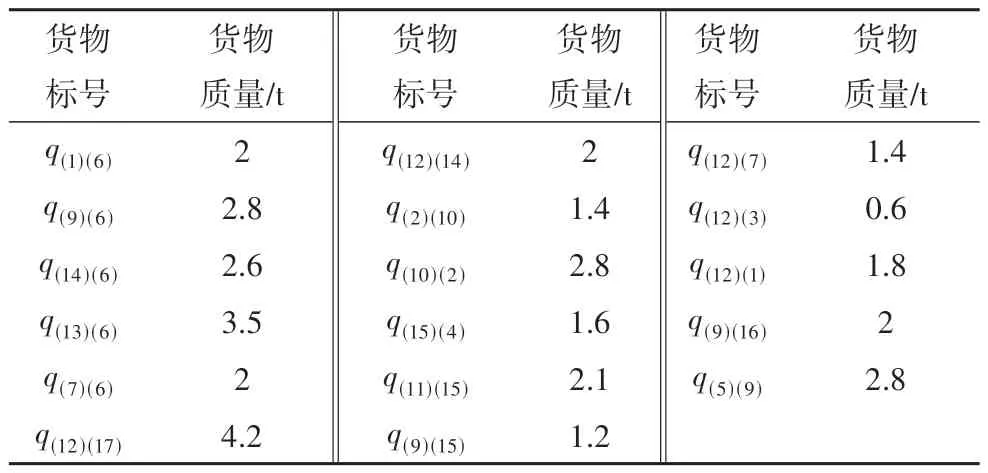
表3 货物信息Tab.3 Cargo information

3.1.2 结果与分析

运用4 种优化算法解决多需求点问题，各算法参数见表4.每种算法实验30 次，最大迭代次数为500 次.WOA-WOA、WOA-ACO 和AOA-ACO 混合优化的特点如下.

表4 各算法参数Tab.4 Parameters for each algorithm

1）WOA-WOA调整参数少、收敛快.

2）WOA-ACO 鲁棒性强.解决混合问题时易于实现.

3）AOA-ACO 全局搜索能力强.较单一算法，求解空间更大.

IAOA-IACO 混合求解相较其他算法，其优势如下.

1）搜索空间大、收敛速度快.IAOA-IACO 较AOA-ACO，算法外层利用对称原则扩大了搜索范围，算法内层通过动态禁忌矩阵减少寻找合理解的迭代次数.

2）跳出局部最优能力强.IAOA-IACO 较WOAWOA 和WOA-ACO，通过概率系数增加算法全局搜索的概率，减少算法陷入局部开发阶段的概率.

实例验证结果见表5.IAOA-IACO 的最优解、平均最优解都优于其他算法，且方差最小，算法的稳定性最好.每种算法的最优解迭代收敛速度曲线见图7，IAOA-IACO收敛速度较快.

表5 4种混合算法计算结果Tab.5 Results of four hybrid algorithms

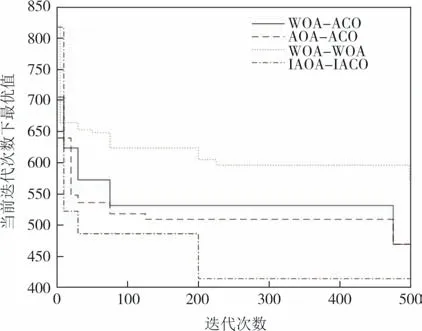
图7 迭代收敛速度曲线Fig.7 Iterative convergence rate curve

图8 最优车辆配送流程Fig.8 Optimal vehicle delivery process

图9 基准函数图像Fig.9 Baseline function image

选择的配送车辆、车辆的最优路径以及装载货物的过程见图 8.横坐标表示车辆经过节点的顺序，车辆在节点装货与卸货情况以及货物的起点、终点和重量都已标注.方框表示货物，加粗的方框表示被转运的货物，标有数字的方框代表被拆分的货物，标有相同数字的方框代表被拆分若干份的同一货物.

车辆1、车辆2、车辆3 的最大装载量分别为 3.5 t、3 t、3.5 t.在图 8（a）中，由于车辆装载量限制，节点2、节点9、节点12被多次访问，车辆第二次经过节点9 之前，装载了需求q(2)(10)，到达节点9 时装载了需求q(9)(15)，到达节点15 时需求q(9)(15)抵达目的地并对其卸货，车辆剩下需求q(2)(10).

在图 8（b）中，标号①的方框代表需求q(13)(6)拆分成3 t和0.5 t，标号②的方框代表需求q(12)(17)拆分成3 t和1.2 t.车辆从节点13 出发时因装载量不足拆分需求q(13)(6)，装载其一部分，到达转运节点12 时卸货并装载需求q(12)(17)的一部分.

在图 8（c）中，车辆在节点12 配送转运到此的需求q(13)(6)，并完成其余任务.

3.2 基准函数测试仿真

3.2.1 案例说明

选择Sphere、Rastrigin、Branin 这3 个基准函数对IAOA、AOA、IACO、ACO 和WOA 进行测试与结果对比.如图 9 所示，Sphere 函数是单峰函数，仅有一个最值，可检测算法收敛能力；Rastrigin 函数是多峰函数，有多个局部最小值，可检测算法跳出局部最优能力；Branin 函数是平滑函数，可检测算法寻优能力，更有代表性.函数的表达式及其自变量的取值范围见表6.函数的最小值分别为0、0、0.398.

表6 基准函数表Tab.6 Table of benchmark function

3.2.2 结果与分析

算法的种群大小设置为30，问题维度为30，最 大迭代次数为1 000.将不同函数运行30 次，其评价指标见表7.分别计算不同基准函数每次迭代的当前最优解的平均值，绘制迭代收敛的半对数曲线，如图10所示.

表7 基准函数测试结果表Tab.7 Table of benchmark function test results

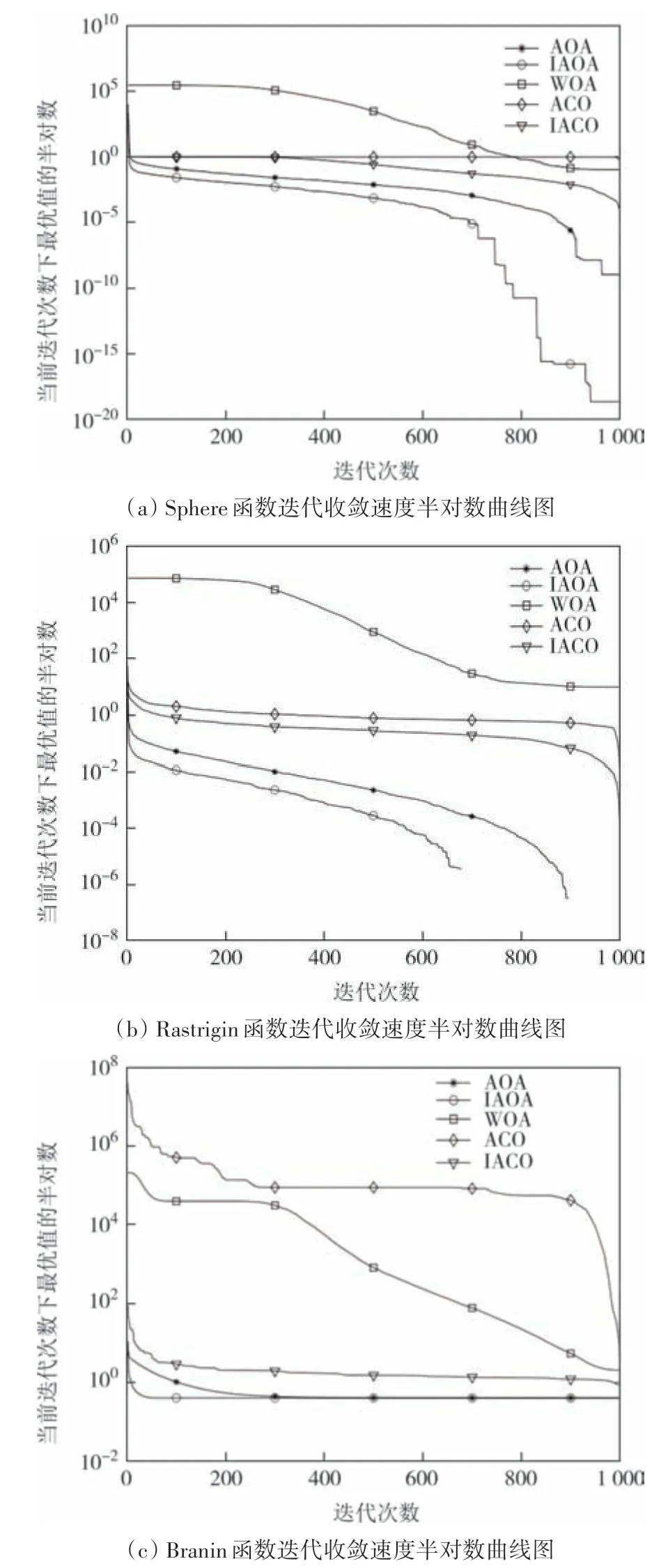
图10 基准函数迭代收敛速度半对数曲线图Fig.10 Semi-log curve of the rate of iterative convergence of the baseline function

在Sphere函数中，IAOA在AOA基础上扩大算法的搜索空间进行改进，其中后期的收敛速度明显快于AOA.通过一定次数的迭代，IAOA 跳出局部最优的能力优势凸显.IACO 在ACO 基础上缩小最优解的范围进行改进，减少了寻找最优解的迭代次数.WOA较其余算法效果不明显.

在Rastrigin 函数中，函数最小值为0，由于0 没有对数，所以IAOA 与AOA 寻找到最小值时对数曲线中断，IAOA 搜索到最优解的迭代次数明显小于AOA.IACO搜索的函数最小值优于ACO.

在Branin函数中，IAOA 较AOA 能在较少迭代次数的情况下获得函数最小值.ACO与WOA获得的函数最小解相近，IACO 获得的函数值优于ACO 与WOA.

4 结语

本文对多需求点问题研究的创新从模型优化、算法改进展开，模型与算法有以下不足.

1）模型中，以车辆总路径最短为目标函数，未考虑时间约束，可能会出现车辆为完成装载或转运货物而提前到达转运节点等待的现象，时间利用率低.

2）算法中，IACO 的改进策略是针对节点多次访问、装载量非线性变化问题提出的，增加了蚂蚁行走每一步筛选有效节点过程的计算，增加了运行时间.

通过对多需求点问题的研究，有以下潜在研究方向.

1）模型中，可考虑将车辆行驶速度与本文问题结合建模，建立车辆行驶时间最短与路径最短的双目标模型.

2）算法中，在迭代过程中向最优解学习，舍弃了差解，算法的改进中可考虑修复差解，利用差解寻找最优解.