基于MILP 的应用服务器集群能耗与性能实时优化

熊智 ，赵敏 ，蔡浩 ，朱长盛 ，许建龙

（1.汕头大学 工学院，广东 汕头 515063；2.汕头大学 科研处，广东 汕头 515063）

在Web 系统中，处理动态请求的服务器称为应用服务器.动态请求对服务器的资源消耗较大，因而大型的Web 系统，例如软件即服务（software as a service，SaaS）应用和大型网购平台等，通常采用应用服务器集群来提供服务.运营商通常按峰值容量部署应用服务器集群，但在实际运行中大多数时候服务器的利用率都很低，浪费了大量能耗.另一方面，应用服务器集群必须提供足够强大的性能以保证服务质量，否则会导致用户流失.在各个行业都节能减排［1-3］和同行竞争日益激烈的环境下，如何根据实际的负载状况实时优化应用服务器集群的部署，以在能耗与性能之间取得平衡是需要解决的重要问题.

CPU 是服务器中能耗最大的部件［4］，借助动态频率调整技术调低其工作频率可以降低其性能和运行功耗［5］.另外，关闭多余的服务器也能有效减少集群功耗［6-7］.有些研究仅依靠动态开关服务器［8-9］，或仅依靠动态调整CPU 频率［10-11］来优化集群的能耗与性能，还有些研究仅依靠任务调度［3］进行优化，它们都无法获得集群最优部署.在优化方法方面，常见的有如下三种：基于控制理论［12］，基于阈值［8，13］和基于规划问题［7，10-11，14-16］的方法.在第一种方法中，由于服务器是一个非常复杂的非线性系统，并且需要同时控制性能和能耗，因而系统模型和控制方案都会非常复杂，需要测定大量的模型参数和控制参数，十分烦琐且可操作性差.至于第二种方法，通常基于排队长度、响应时间或利用率等阈值，采用启发式的方法调整服务器的开关和CPU 频率，它们无法获得最优的部署.第三种方法将集群优化描述成规划问题，然后求解，该方法因能获得最优或者次优的部署而被广泛采用.

虽然在基于规划问题的集群优化方面已有一些较好的成果，但它们存在两方面的不足.第一方面是优化的性能指标.绝大多数相关研究都关注响应时间［8，11，14，16-18］而忽略了请求的丢弃，因为在无限容量的排队模型中，响应时间的公式较为简单，容易优化.然而在实际的Web系统中，Web请求的响应时间很短且服务器端通常采用多层结构，因而响应时间在很大程度上取决于用户的网络环境并且很难量化地进行优化.此外，实际的应用服务器当并发请求数达到预设的上限时会不再接受新的请求，因而并非是无限容量的.在这些研究中，文献［8］、［14］和［16］为请求的平均等待（或响应）时间设置上限，并将其作为约束条件，文献［11］以最小化请求的平均响应时间为优化目标.另外，文献［15］在给定功耗预算的前提下最大化评价函数，评价函数综合考虑了服务器的性能和效率.文献［3］考虑了服务器的CPU 利用率，根据其值动态计算服务器的能耗效率.文献［17］虽然对集群能耗与请求丢弃率进行了综合优化，但存在下面第二方面的不足.

第二方面的不足在于优化的实时性.集群优化通常是一个复杂的NP-Hard 问题，过长的求解时间会导致过高的性能违约率［19］，并且当负载快速波动时需要及时调整集群部署，因此优化问题必须被快速求解.规划变量的定义和规划问题的求解是影响优化实时性的两个重要方面.已有的研究通常针对每个服务器定义变量［11，20］，有的甚至为每个服务器的每个频率定义变量［7，21］.在这些研究中，变量数目随着集群规模的变大而增加，从而导致大规模集群的优化问题无法实时求解.一般来说，集群中服务器型号的数量通常比服务器的数量低一到两个数量级，因为服务器通常是按型号一批一批地采购，如果能针对服务器的型号定义变量，变量数目将大幅度减少.然而，有些研究仅考虑完全同构（即所有服务器同型号）的集群［10，22］，它们的应用范围很有限.在规划问题的求解方面，有些研究仅采用启发式或贪婪算法求解［15，23-24］，虽然求解速度快，但服务器参数和集群负载对求解质量影响很大.有些研究采用智能优化算法求解［25-27］，然而其求解效率严重依赖算法参数的选择，并且无法保证能够得到全局最优解.还有些研究虽然提出了一些求解方法，但并未对求解效率进行测试［28］.此外，有些研究关注高性能计算集群的优化［29-30］，但Web 请求与高性能计算任务不同，它们是短寿命的和大量的，因此资源无法被精确分配给每个Web请求.

针对上述不足，本文提出一种基于混合整数线性规划（mixed integer linear programming，MILP）的应用服务器集群能耗与性能实时优化方案，根据集群实际负载的大小动态调整各服务器的开关、CPU 频率和负载.该方案结合采用线性加权法和主目标法来优化集群功率与请求丢弃率这两个目标，将双目标优化转换成一个带约束的单目标优化.我们首先基于服务器负载-功率曲线的特性得到两个结论，进而定义很少的变量将集群优化描述成一个混合整数二次规划（mixed integer quadratic programming，MIQP）问题，然后采用变量拆分和变量转换将其转化成MILP 问题，最后采用Gurobi 优化器［31］进行高效精确地求解.特殊顺序集（special-ordered set，SOS）约束的引入使得求解时间更加稳定，而CPU 频率调整的进一步优化大幅度减少了CPU 频率的切换.多种场景下的测试结果验证了所提出方案的可行性和有效性.

1 系统模型及分析

本文提出的优化方案采用基于规划问题的优化方法.在每个优化阶段结束时，优化控制器首先预测下个阶段的集群负载（即平均请求到达速率），然后将其带入规划问题进行求解，最后依据求解结果调整集群中各服务器的部署和负载分配方案.目前关于预测模型和Web 负载预测的研究已有很多，这不在本文的讨论范围内.

1.1 集群能耗与性能优化模型

假设预测的集群负载为L.用S表示集群中所有服务器的集合，服务器s的负载和功率分别记为Load（s）和Power（s）.考虑如下集群能耗与性能双目标优化：

第一个目标为集群的功率，第二个目标为集群的请求丢弃率，希望它们都尽可能小.

线性加权法和主目标法为多目标优化的两种常用方法，前者将多个子目标通过线性加权变成一个目标，后者选择最重要的一个子目标作为优化目标，并通过引入上界将其余子目标转化为约束条件.本文结合这两种方法，将集群能耗与性能优化描述如下：

目标函数（3）由两部分加权构成，前者为集群每秒的耗电量（即功率），后者为集群每秒的请求丢弃数，加权系数δ用于调节这两部分的重要程度.注意，这里将式（1）中的第二个目标由请求丢弃率改为了每秒的请求丢弃数，以使得两个目标描述的都是每秒的指标，从而使意义较为明确.并且，请求丢弃率和每秒的请求丢弃数之间只差一个比例常数（L是已知的），所以上述目标的修改相当于只是改变了权重的值，而权重本身是可调的.约束条件（4）的左边部分是约束条件（2）的变形，右边部分则是为第二个优化目标请求丢弃率引入的上界U.在实际应用中，过高的请求丢弃率会造成用户流失，因此为请求丢弃率设置一个上界十分必要且具有很好的实际意义.U和δ的值可根据实际应用场景进行设置.尤其是当U=0、δ=1 时，上述优化就变成了性能保证下的能耗优化.优化方案的示意图如图1所示.

图1 优化方案示意图Fig.1 Schematic of the optimization scheme

一旦依据求解结果部署好各服务器的开关和CPU 频率，对于每个到达分配器的请求，它将以［L-∑Load（s）］/L的概率被丢弃，以Load（s）/L的概率调度给服务器s.具体调度算法可以采用轮盘赌或者加权轮转来实现.

1.2 CPU频率调整模式和服务器负载-功率模型

现在的CPU 通常都会提供一组电压和频率对的集合供用户选择，选择较低的电压和频率可降低CPU 的性能和运行功率.另外，现在主流的CPU 都是多核结构，为了便于能耗与性能的优化控制，和众多研究一样我们让其所有核的频率同时调整且保持相同.

CPU 可供选择的频率本文称为离散频率.当一台服务器工作在某个离散频率上，在请求丢弃率低到能忽略的情况下，它能承担的最大平均请求速率被定义为该频率的满载负载，承担满载负载时的功率称为该频率的满载功率.假设集群中的服务器有M个型号Ti（1≤i≤M），Ti型号服务器的相关参数如表1所示.

表1 Ti型号服务器的相关参数Tab.1 The related parameters of servers of type Ti

对于一台Ti型号的服务器，假设该服务器分配到的负载为l，Li，j＜l＜Li，j+1，为了保证不超载，应当让其CPU 最低工作在离散频率Fi，j+1上，但此时其能力过剩，无法最大限度地节能.为了更加细粒度地控制能耗与性能，本文采用如下方法让CPU 频率等效连续调整从而让CPU 满载工作：若一台Ti型号的服务器分配到的负载为l，Li，j≤l≤Li，j+1，则让其CPU 频率在Fi，j和Fi，j+1之间切换，且工作在Fi，j和Fi，j+1上的时间分别占（Li，j+1-l）/（Li，j+1-Li，j）和（l-Li，j）/（Li，j+1-Li，j）.此时，该服务器的等效频率为

1.3 针对服务器型号定义变量的可行性

根据式（5）和式（6）可推导出服务器的频率-负载模型loadi（f）和频率-功率模型poweri（f），前者为一系列点（Fi，j，Li，j）的分段线性插值，后者为一系列点（Fi，j，Pi，j）的分段线性插值.根据这两组点的凸凹性可证明如下两个结论［27］.

结论1对于所有承担负载在同一区间［Li，j，Li，j+1］的Ti型号服务器，让它们承担相同的负载可以得到集群能耗与性能优化的最优部署.

结论2对于开启的所有Ti型号服务器，让它们承担相同的负载可以得到集群能耗与性能优化的最优部署.

基于结论1，可以针对每个服务器型号的每个负载区间定义变量.基于结论2，可以针对每个服务器型号定义变量，进一步减少变量的数目.

2 基于MIQP的优化方案

基于结论2，本节针对每个服务器型号定义变量，将集群能耗与性能优化描述成一个MIQP 问题，然后设计求解方案.

2.1 优化问题的描述

针对Ti型号的服务器定义两个变量：整数ni和实数li，表示有ni台该型号的服务器开启且以li的负载提供服务.引入变量pi=Poweri（li），那么优化模型（3）和（4）可描述成如下规划问题：

式中：ni为整数变量，li和pi为实数变量，目标函数（7）和约束条件（8）均包含两个变量的相乘，故该问题是一个MIQP问题.该规划问题只需为每种服务器型号定义三个变量，变量数目非常少.注意到式（9）是一个函数型约束，虽然该约束本身比较复杂，但其引入使得目标函数（7）变得简单，使上述问题变成了一个标准形式的二次规划问题，便于采用已有的优化器进行求解.

2.2 基于Gurobi优化器的求解方法

很多相关研究讨论的是在保证性能的前提下最小化集群能耗，这类研究由于只有能耗一个优化目标，因而可以采用启发式策略得到较好的次优解，例如，优先开启能耗效率高的服务器并让其承担尽可能大的负载（以关闭尽可能多的能耗效率低的服务器），或者优先开启能耗效率高的服务器并让其工作在能耗效率尽可能高的频率和负载上（以取得尽可能高的能耗效率）.然而，这里的优化目标（7）是集群能耗和性能的加权值，无法采用类似的启发式策略求解.

Gurobi 是由Gurobi 公司开发的新一代大规模数学规划优化器，支持MILP 和MIQP 等问题的精确求解，并提供C 和Python 等语言的API（application programming interface，应用程序接口）.Gurobi 支持多种类型的函数型约束，其中包括分段线性函数，因而能够描述约束（9）.为了加快求解速度，我们采用Gurobi 的C 语言API 实现了对规划问题（7）～（11）的求解.但该方法在一些场景下求解时间较长，无法满足集群实时优化的需求（参见4.2 节中的测试）.由于线性规划问题的求解开销较小，并且式（7）～（11）是一个二次问题且变量间存在分段线性的关系，因此我们希望能将其转化成线性规划问题进而求解.

3 基于MILP的优化方案

针对MIQP问题（7）～（11）的特点，本节通过变量拆分将分段线性函数变为线性函数，通过变量转换去掉变量的相乘，将该问题转化为一个MILP 问题.接着，本节引入SOS约束，并对CPU 频率调整做进一步的优化.

3.1 变量拆分

在式（7）～式（11）中，整数变量ni和实数变量li表示有ni台Ti型号的服务器在以li的负载提供服务.Poweri（li）是一个分段线性函数，它在每个负载区间［Li，j，Li，j+1］上是线性函数，这种负载区间有Ci-1 个，因此我们将ni和li各拆分成Ci-1 个变量ni，j和li，j，j=1，2，…，Ci-1，表示有ni，j台Ti型号的服务器在以li，j的负载提供服务，其中li，j∈［Li，j，Li，j+1］.这相当于仅使用结论1 来针对每个服务器型号的每个负载区间定义变量.根据结论2 可知，对于每个i，可让ni，j中至多只有一个不为零，j=1，2，…，Ci-1.

记

则式（7）～式（11）可重写如下：

3.2 变量转换

在优化问题（13）～（18）中，目标函数和约束条件中存在的二次项仅为ni，jpi，j和ni，jli，j，由于pi，j和li，j之间为线性关系，故ni，jpi，j和ni，jli，j之间也是线性关系，我们希望通过合适的变量转换将ni，jpi，j和ni，jli，j均变成线性函数.

根据1.2 节的描述，（Li，j+1-l）/（Li，j+1-Li，j）和（l-Li，j）/（Li，j+1-Li，j）分别表示服务器工作在频率Fi，j和Fi，j+1上的时间占比，我们将（l-Li，j）/（Li，j+1-Li，j）称为切换因子，并记为η.显然切换因子η∈［0，1］，并且通过切换因子η能够计算出负载l.前面对Ti型号服务器的每个负载区间［Li，j，Li，j+1］定义两个变量ni，j和li，j.我们用变量ηi，j替换掉变量li，j，它表示这ni，j台服务器的总切换因子，也就是说这ni，j台服务器的切换因子均为ηi，j/ni，j，即

根据式（12）、式（15）和式（19）可进行如下推导：

则式（13）～式（18）变为：

目标函数（22）是线性的，约束条件（23）～（25）也都是线性的，因此上述模型是一个MILP 问题.我们同样采用Gurobi 优化器对该MILP 问题进行求解.并非所有的二次规划都能转化成线性规划，这取决于具体问题的形式.这里给出的转换方案对变量间存在线性约束的规划问题提供了一种参考求解方案.

3.3 SOS约束

虽然求解MILP 问题（22）～（27）能得到集群的最优部署，但该问题的描述没有使用结论2.在3.1节中已分析到，如果使用结论2，那么可以增加如下约束：对于每个i，ni，j中至多只有一个不为零，j=1，2，…，Ci-1.SOS 约束是一种高度专业化的约束，对给定有序集合里的变量可以接受的值进行限制.SOS约束有两种类型，其中SOS1 型约束用于规定一个变量集合中最多只允许一个变量取非零值.Gurobi 优化器提供GRBaddsos 函数给规划问题增加SOS 约束，因此我们采用该函数为变量ni，j增加SOS1型约束.虽然增加该SOS 约束与否并不会影响集群优化的结果，但其在一些场景下可以提高规划问题的求解效率.

注意到，Li，j同时属于区间［Li，j-1，Li，j］和［Li，j，Li，j+1］.假设在优化结果中有10 台T0型号的服务器开启，它们的工作频率为F0，2，负载为L0，2.如果不采用SOS 约束，求得的解可能为：n0，1=4，η0，1=4，n0，2=6，η0，2=0，其他n0，j（j≠1 和2）均为0.如果采用了SOS 约束，则不可能出现上述情形，只会要么n0，1=10，η0，1=10，其他n0，j（j≠1）均为0，要么n0，2=10，η0，2=0，其他n0，j（j≠2）均为0.

3.4 CPU频率调整的进一步优化

上述方案对Ti型号服务器的每个负载区间［Li，j，Li，j+1］定义了两个变量ni，j和ηi，j，表示开启的ni，j台服务器的CPU 频率均在Fi，j和Fi，j+1之间切换，且时间占比分别为1-ηi，j/ni，j和ηi，j/ni，j.虽然CPU 频率的切换可以通过调用CPUFreqUtils 工具包提供的函数实现，但会有一定的开销，并且过于频繁地切换CPU 频率有可能影响CPU 寿命.根据式（19）可知，这ni，j台服务器的总负载为

根据式（12）、式（15）和式（19）可知，这ni，j台服务器的总功率为

注意到ηi，j≤ni，j，下面根据ηi，j的优化结果分两种情况对这ni，j台服务器的部署进行调整.

情况1：ηi，j为整数.将ηi，j台的负载调整为Li，j+1，CPU 频率调整为Fi，j+1；将ni，j-ηi，j台的负载调整为Li，j，CPU频率调整为Fi，j.

情况2：ηi，j不为整数.将ηi，j」（*」表示向下取整）台的负载调整为Li，j+1，CPU 频率调整为Fi，j+1；将ni，j-ηi，j」-1台的负载调整为Li，j，CPU 频率调整为Fi，j；将剩下1 台的负载调整为［1-（ηi，j-ηi，j」）］Li，j+（ηi，j-ηi，j」）Li，j+1，CPU 频率在Fi，j和Fi，j+1之间切换，且时间占比分别为［1-（ηi，j-ηi，j」）］和ηi，j-ηi，j」.

容易验证，经上述部署调整后，这ni，j台服务器的总负载和总功率均保持不变，但至多只有一台服务器的CPU 频率需要在Fi，j和Fi，j+1之间切换，大幅度减少了CPU 频率的切换.进一步地，在上述情况2中，可以直接让最后的那一台服务器也工作在频率Fi，j+1上，虽然这样会多消耗一点点的能耗，但换来的是（在一个优化周期内）无需切换CPU频率.

4 测试

本节首先分别测试基于MIQP 和基于MILP 的优化方案的求解时间，尤其展示将MIQP 转换成MILP和引入SOS 约束这两个措施的效果，最后将提出的方案与已有的基于MILP的方案进行对比测试.

4.1 测试环境

表2 列出了6 种服务器的频率、性能和功率数据［7，27］，各服务器的待机功率约为3.5 W.我们使用3个不同规模的集群进行测试，它们均由这6 种型号的服务器构成，各型号的数量相等，分别为40、160和640 台，即这3 个集群的规模分别为240、960 和 3 840台服务器.请求丢弃率的上限U设置为10%.优化控制器为Intel Core I7-6700 CPU 和32G 内存的PC机，安装Windows 10系统，Gurobi的版本为9.1.2.

表2 各型号服务器的频率、性能和功率数据Tab.2 Frequency，performance，and power data for each server type

4.2 基于MIQP优化方案的求解时间

对于一个集群来说，各个服务器最高频率的满载负载之和为该集群能承担的最大负载，称为集群最大负载.下文用集群实际负载与集群最大负载的比值来表示负载的大小，例如，50%的集群负载是指集群负载等于集群最大负载的50%.

集群规模，集群负载，以及加权系数δ都对规划问题的求解时间有影响.在每个集群规模下，我们用20%、50%和80%三种负载测试基于MIQP 优化方案的求解时间；在每种负载情况下，又让加权系数δ以0.01 的间隔从0 变到1.每个场景下的测试重复10次，求解时间取平均值，测试结果见图2.

图2 MIQP方案的求解时间Fig.2 Solution time for the MIQP scheme

从图中可以看到，大致上求解时间随着集群规模的增大而变长，这主要是因为规划变量ni的范围变大了，而求解时间与集群负载和加权系数之间没有明显规律.绝大多数场景下的求解时间超过了50 ms，有些场景下的求解时间甚至接近4 s，因此基于MIQP 的优化方案无法保证优化的实时性.

4.3 基于MILP优化方案的求解时间

接下来测试基于MILP 优化方案的求解时间.为了分别展示将MIQP 转换成MILP 和引入SOS 约束这两个措施的效果，本小节先不采用SOS 约束，而在下个小节专门测试引入SOS 约束的效果.与4.2 节一样，在每个集群规模和集群负载下，我们让加权系数δ以0.01 的间隔从0 变到1 分别进行测试，然后将求解时间的平均值、中值、最小值和最大值与基于MIQP 的方案进行对比，测试结果见表3.表3 中的结果表明，无论是求解时间的平均值和中值，还是最小值和最大值，基于MILP 的优化方案均明显低于基于MIQP的优化方案，尤其是平均值和中值降到了10 ms左右.然而对比最大值和中值来看，基于MILP 的优化方案的求解时间不太稳定，在某些场景下最大值为中值的11倍多.

表3 变为线性规划后求解时间的降低Tab.3 Reduction of solution time after changing to linear programming

4.4 引入SOS约束的效果

本小节的测试场景（包括集群规模、集群负载和加权系数）与前两个小节一样.对于每个场景，分别测试不采用SOS 约束和采用SOS 约束这两种情况下基于MILP优化方案的求解时间，结果见图3.

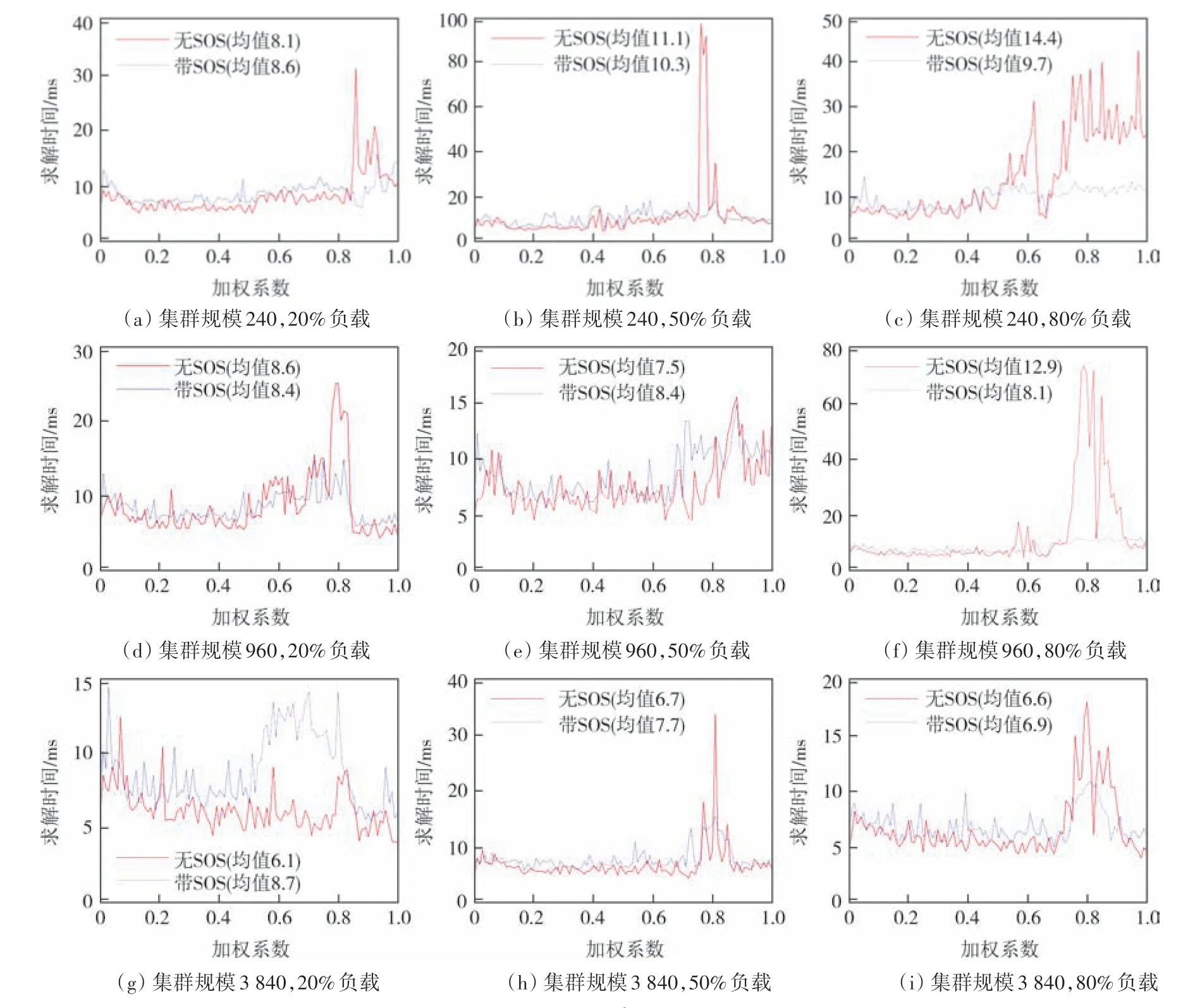
图3 SOS约束的效果Fig.3 The effect of the SOS constraint

在图3 的子图（a）、（e）、（g）、（h）和（i）中，采用SOS约束后平均求解时间变长了.这是因为在这5幅子图中不采用SOS 约束时的求解时间已经很小（平均值不超过8.1 ms），SOS 约束的引入使得模型本身变得更加复杂，从而导致求解时间略有增加.在其他4幅子图中，采用SOS约束均使得平均求解时间有所缩短，尤其在子图（c）和（f）中，平均求解时间从14.4 ms和12.9 ms分别缩短为9.7 ms和8.1 ms.

当不采用SOS 约束时，求解时间在一些场景下会突然变得很长，而当引入了SOS 约束后，求解时间则比较稳定.该现象在子图（a）、（b）、（c）、（d）、（f）、（h）和（i）中非常明显.

综合来看，由于不采用SOS 约束时的求解时间已经很短，故引入SOS 约束对平均求解时间没有明显的改善，但其使得求解时间变得稳定，能更好地保证求解的实时性.

4.5 与其他基于MILP方案的对比

文献［7］和［21］针对每个服务器的每个频率或每对相邻频率区间定义3 个变量，其中2 个实数变量，1 个二进制变量，进而将集群能耗与性能优化描述成MILP 问题.我们采用该变量定义方式（即针对服务器定义变量）将模型（3）～（4）描述成一个MILP问题，并采用Gurobi优化器进行求解.我们对该方案进行了测试，测试场景和方法与4.3 节、4.4 节一样.由于过长的求解时间没有实用价值，因此求解时间的上限设置为1 min.该方案与本文基于MILP 的方案在变量数目上的对比见表4，在求解时间上的对比见表5.在表5 中，超时场景的求解时间不参与平均值、中值、最小值和最大值的计算，超时率等于超时场景数除以每个集群规模和负载下的总场景数101.

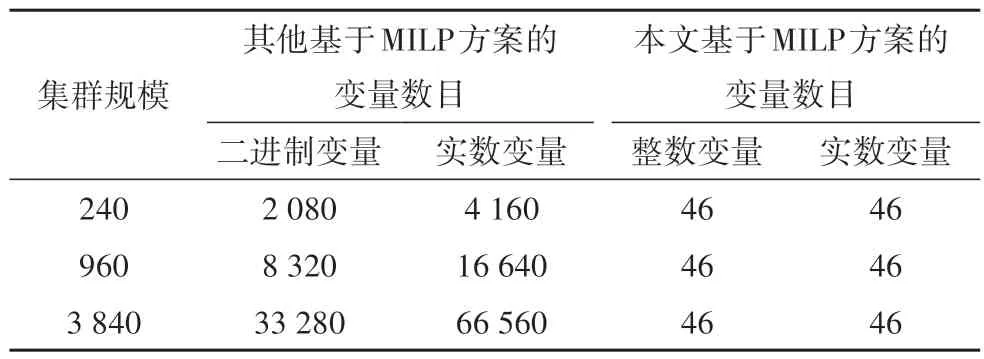
表4 变量数目对比Tab.4 Comparison of the number of variables

表5 求解时间对比（U=10%）Tab.5 Comparison of solution times（U=10%）

在前面的测试中，请求丢弃率的上限U被固定为10%.为了更加全面地测评本文方案的求解实时性，我们对U取5%和15%的情形也分别进行了测试，结果见表6和表7.

表6 求解时间对比（U=5%）Tab.6 Comparison of solution times（U=5%）

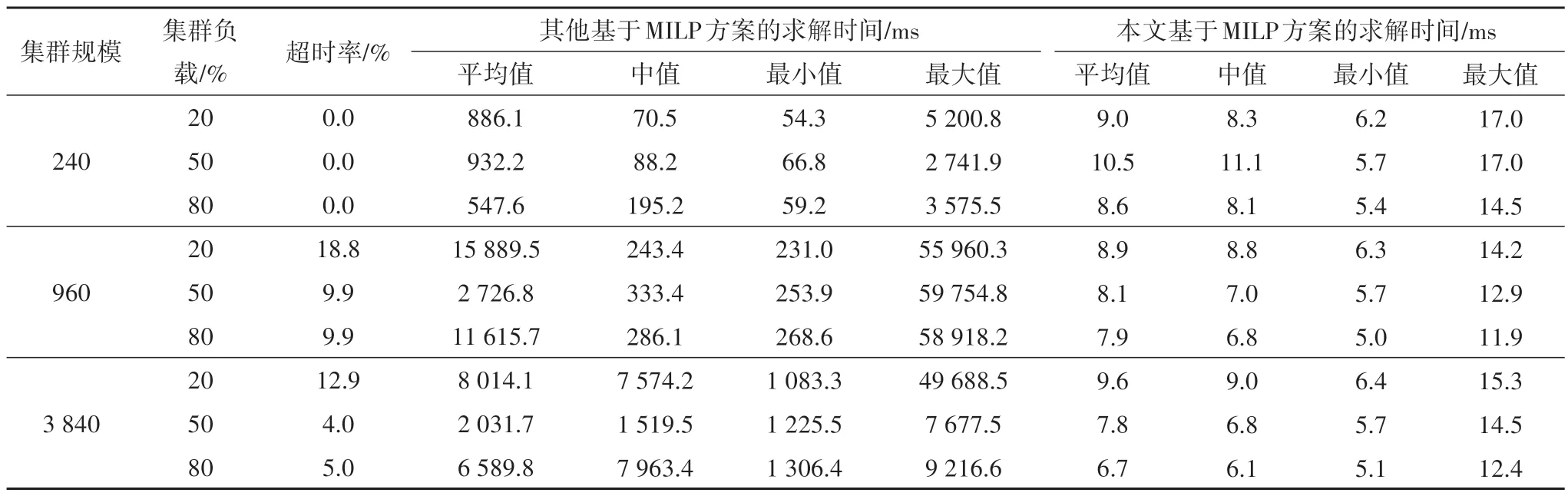
表7 求解时间对比（U=15%）Tab.7 Comparison of solution times（U=15%）

在表4 中，由于其他基于MILP 的方案针对服务器定义变量，因而当集群规模变大时，变量的数目随之增加.而本文基于MILP 的方案针对服务器型号定义变量，只要集群中服务器的型号没发生变化，变量的数目就不会发生变化.因为本文基于MILP 方案的变量数目少，因此在表5～表7 中，无论是求解时间的平均值和中值，还是最小值和最大值，本文的方案均优于其他基于MILP 的方案.尤其当应用于后两个规模较大的集群时，其他基于MILP 的方案均出现了一些求解时间超时的情形.此外，从表5～表7 中还可以看到，当U取5%和15%时，本文方案的求解时间及其波动程度均与U取10%时的相当，因此U值的设置不会对本文方案的优化实时性产生影响.

5 结论

本文首先结合线性加权法和主目标法设计了一种应用服务器集群能耗与性能优化模型，然后基于服务器负载-功率曲线的特性得到了两个结论，进而提出了两种优化方案：基于MIQP的优化方案与基于MILP 的优化方案，它们均采用Gurobi 优化器对规划问题进行精确求解.前者只须针对每种服务器型号定义3 个变量，因而变量数目很少，但由于是非线性问题，当应用于集群规模很大的一些场景时求解时间过长.后者针对MIQP 问题的特点，采用变量拆分和变量转换将其转化成一个MILP 问题，并引入了SOS 约束.测试结果表明，将MIQP 转换为MILP 后，平均求解时间降到了10 ms左右，而SOS约束的引入使得求解时间更加稳定，能够保证规划问题的实时求解.与已有的基于MILP 的优化方案相比，本文提出的方案大幅度减少了变量数目并缩短了求解时间.此外，本文虽然让CPU 在相邻离散频率之间来回切换以等效工作在连续频率上，并在该模式下建立服务器功率模型和集群优化模型，但在最终部署时对CPU 的频率调整做了进一步优化，大幅度减少了CPU 频率的切换.接下来，我们将研究如何根据应用场景的不同选择合适的加权系数.