一种OFDM 稀疏信道估计系数优化方案

朱俊杰，刘昊，郑志安

（中南林业科技大学 计算机与信息工程学院，湖南 长沙 410003）

正交频分复用（orthogonal frequency division multiplexing，OFDM）调制技术由于其高效的频谱利用率和抗多径干扰能力，已经被广泛研究于各种无线通信系统中［1］.尽管如此，由于无线信道中多径效应会引起严重的频率选择性衰落，接收机仍然需要基于比较精确的信道状态信息才能从接收信号中解调出用户数据.大量的实验数据表明，多路径信道的大部分能量几乎都集中在极少的信道抽头上，因此它具有稀疏特性［2］.目前作为研究热点的毫米波由于其衰落特性，其信道相比现有的电磁波具有更加明显的稀疏特性［3］.压缩感知理论方法在解决稀疏信号重构问题上，相比传统的采样方法具有高效和准确的优势.因此，基于压缩感知的稀疏信道估计因其高效的频谱利用率和良好的估计性能受到广大研究者的重视［4-8］.

稀疏信号恢复问题是OFDM 稀疏信道估计技术中的重要研究议题.其中以正交匹配追踪（orthogonal matching pursuit，OMP）算法［8］为代表的贪婪算法以迭代的方式恢复信号，具有复杂度低的突出优点.这些算法在每次迭代中通过原子选择来搜索局部最优解，力求在算法结束时找到全局最优解［7-12］.对于OFDM 稀疏信道估计来说，每次迭代中的原子选择过程对应多径信道的时延估计，利用选取到的原子集进行的信号重构则对应多径信道抽头系数的估计.OMP 算法在每次迭代中仅从感知矩阵里选择一个原子，其恢复性能对于原子的选择十分敏感［10］.为了缓解这一敏感性，压缩采样匹配追踪（compressive sampling matching pursuit，CoSaMP）算法［11］和阶段确定匹配跟踪（stage-determined matching pursuit，SdMP）算法［6］增加搜索步长并运用回溯剪枝的思想，改进了原子选择的方式.上述几种算法都十分依赖于信道稀疏度先验信息，然而在实际情况中信道稀疏度信息是很难事先估计的.对此，研究者们提出了稀疏度自适应匹配追踪（sparsity adaptive matching pursuit，SAMP）算法［12］和一种新的自适应匹配追踪（new adaptive matching pursuit，NAMP）算法［7］，力求在无须事先获知信道稀疏度信息的情况下，也能具有较好的估计性能.

以上几种算法主要是针对原子选择方式的优化，即稀疏信道时延估计问题的改进.完成路径时延估计后，贪婪算法利用已经估计出来的路径时延来计算对应时延位置上的信道抽头系数值.然而，由于原子之间的非正交性以及随机噪声的影响，稀疏信号恢复算法对衰落较大的路径不可避免地会发生错误的时延估计.对此，本文围绕如何降低错误时延估计对稀疏信号估计恢复结果的影响展开研究.

通过对OMP 算法中抽头系数估计的分析，发现抽头系数的估计结果主要受到原子集估计的影响.而在原子选择错误的情况下，对应错误抽头位置上的信道系数会被过高估计，从而严重影响稀疏信道估计的精确度.为了提高抽头错误估计时的恢复性能，本文提出了一种针对贪婪算法的系数优化方案（coefficient optimization scheme，COS）.该方案利用了相邻符号信道间路径时延的相关特性，体现为相邻OFDM 符号的信道间多径个数和路径时延呈现低时变，而路径上的复增益呈现高时变并受到瑞利衰落的影响［13］.在该方案中，当前OFDM 符号引入相邻符号时间信道上的估计结果，并基于l2范数最小化的准则选择最优的系数估计.最后，本文将COS分别运用至OMP 算法与SAMP 算法中，测试了所得到的系数优化 OMP（Coefficient optimization-orthogonal matching pursuit，CO-OMP）算法与系数优化 SAMP（coefficient optimization-sparsity adaptive matching pursuit，CO-SAMP）算法的性能.仿真结果表明，相对于OMP 和SAMP，CO-OMP 和CO-SAMP 都有较为可观的提升.

1 稀疏信道估计模型

无线多径信道的稀疏特性体现在信道冲激响应的绝大部分能量集中在少数的信道路径上.该稀疏信道可以表示为一个长度为L的有限冲激响应滤波器：

其中，下标n表示OFDM符号序号.hn仅在抽头ui（1 ≤i≤S，0 ≤ui≤L-1）上具有非零复增益hn，ui，即hn[ui]=hn，ui.S为信道稀疏度，且S＜＜L.设定一个快速傅里叶点数为N的OFDM 系统，则所有频点处的频率响应可以表示为

其中，G∈CN×L是N阶傅里叶矩阵前L列构成的子矩阵.稀疏信道估计的目的是估计出抽头位置Δn={u1，u2，…，uS} 和对应的信道系数={hn，u1，hn，u2，…，hn，uS}，从而恢复出hn和fn.

假设导频数量为M，导频子载波位置集合为p={p1，p2，…，pM}.导频位置处得到的频率响应作为稀疏恢复的观测向量yn∈CM×1.根据压缩感知理论，原信号的观测向量可以由对应感知矩阵中的原子进行稀疏线性表示.因此，可以基于公式（2）获得yn的稀疏表示：

其中，wn为随机噪声.感知矩阵Ψ∈CM×L为G以集合p中的元素为索引提取出来的行向量构成的子矩阵.Ψ=[ψ0，…，ψl，…，ψL-1]，其中列向量ψl∈CM×1称为感知矩阵Ψ的原子，0 ≤l≤L-1.定义Ψ的互相关性为

Ψ的构造满足互相关最小原则：根据已知的导频个数M寻找一个导频位置集合p，使得由G得到的感知矩阵Ψ拥有最小的互相关性μ（0 ＜μ＜1）［14］.

由公式（3）可知，hn可以由接收端已知的yn和Ψ通过稀疏恢复算法估计得到.

2 时延估计误差的影响

算法1 给出了贪婪迭代算法中具有代表性的OMP 算法的伪代码.算法1 假设信道稀疏度S已知，由此令迭代次数k=S（1 ≤k≤S）时算法终止.其中分别表示第k次迭代中得到的原子集估计和信道系数估计.

OMP 算法的第k次迭代主要由原子选择、系数估计两个步骤组成.

经过S次迭代，OMP 算法根据抽头位置估计和对应的系数估计恢复信道冲激响应.若OMP 在迭代过程中选择了错误的原子，会导致稀疏估计结果与实际值之间出现较大的偏差.假设第n个OFDM 符号的信道路径数为S=2，真实的抽头位置为Δn={u1，u2}.若OMP 的支撑集估计正确，此时的原子集可以表示为An=[ψu1，ψu2].LS 的系数估计结果为：

由于M和μ都是固定值，系数估计的结果主要受相关运算的结果影响.由于残差的不断更新，残差中剩余路径的能量逐渐减小，且受到更多的噪声影响.当第二条路径的抽头位置通过算法1 中的步骤2 被错误估计成e时，An=[ψu1，ψe].LS的系数估计结果变为

错误抽头位置e上的系数被过高估计.而感知矩阵Ψ经过特定算法构造后，其互相关性μ通常小于0.3［14］，因此真实抽头位置上的系数估计|β'u1|≈|βu1|.由此可见，由于错误时延上路径系数的过高估计，其最终的系数估计结果通常具有更大的l2范数：

3 信道抽头系数优化方案

对于路径抽头位置发生错误估计的情况，我们希望在错误的抽头位置上得到较小的系数估计值，以降低稀疏信号恢复的误差.抽头位置上的系数估计主要受到对应原子和观测向量yn的相关运算的影响.与yn越相关的原子，其对应抽头位置上的系数估计值越大.由OMP 算法的原子选择过程可知，贪婪追踪算法每次迭代选取与yn的残差最相关的原子，因此当前符号所得到的原子集中的原子都与yn具有很强的相关性.

在移动通信中，相邻符号间多径信道的路径数和路径时延具有时域相关性.可以认为在两个OFDM 符号时间内，信道路径时延保持不变.因此，同一信噪比下相邻符号的抽头位置估计结果具有相似的结构：包括由于路径能量较高被正确估计的抽头位置，和由于信道随机噪声影响而产生的不同的错误位置估计.假设第n个OFDM符号和前一个符号在迭代选择原子时，受随机噪声的影响都发生了错误选择.将二者的观测向量进行抽头位置估计后的结果分别表示为Δn-1={u，en-1}和Δn={u，en}.其中u={u1，u2，…，uS-D}表示正确的抽头位置估计.en={en，1，en，2，…，en，S-D}表示第n个符号上的错误的抽头位置估计，en-1同理.D∈{1，2，…，S}为S个非零抽头中发生错误估计的数量.由于噪声的随机性，错误选择的位置各不相同，满足en-1≠en.对于同一符号的观测向量yn，基于Δn-1和Δn两种不同抽头位置估计恢复的信道系数可以表示为

由此可见，通过引入相邻符号的抽头估计结果Δn-1来对当前符号进行稀疏重构，可以自适应地降低错误原子分量上系数的过高估计，并且体现为系数估计结果的l2范数的减小.算法2展示了本文基于上述思想所提出的系数优化方案的伪代码.

为了避免恶劣的抽头估计结果对本符号稀疏重构的影响，该方案不直接输出由当前符号的抽头估计结果得到的系数估计，而是通过引入相邻符号的抽头估计，并选取具有最小l2范数的系数估计作为系数优化的结果.

4 实验仿真

在本节中，首先基于OMP 算法和SAMP 算法验证了COS抑制错误原子分量上系数过高估计问题的可行性.随后通过归一化均方误差（normalized mean square error，NMSE）性能测试了COS 对于OMP 和SAMP 的性能增益，其中NMSE 的公式定义为.仿真假设OMP 算法已知信道稀疏度先验信息，最大迭代次数设置为信道的稀疏度.SAMP 算法无须事先获知信道稀疏度先验信息，基于当前迭代更新后的残差能量与理想的信道噪声能量先验信息的比较作为迭代停止条件的判断依据，并且更新步长大小设置为1［12］.作为比较，本文也将讨论存在非理想信道噪声能量估计3 dB误差下的SAMP 算法的性能.本文分别采用了4GLTE 中的EPA 信道模型和EVA 信道模型［15］，以及随机多路径信道模型进行性能仿真.随机路径信道模型的路径数和离散路径延迟服从均匀分布，路径增益服从瑞利分布.导频辅助的OFDM系统参数如表1所示.

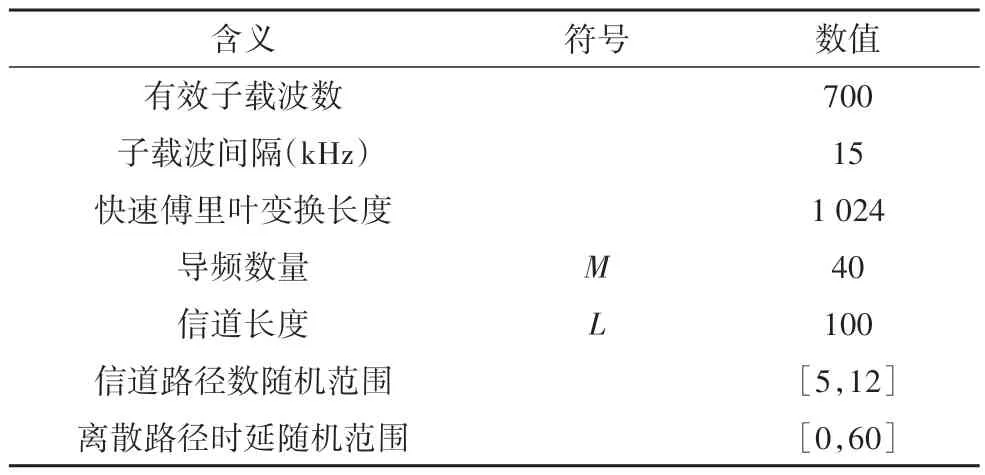
表1 OFDM 系统参数Tab 1 OFDM system parameters

图1 和图2 分别比较了同一信噪比（signal-tonoise ratio，SNR）下的OMP 算法和SAMP 算法，以及使用了COS 的CO-OMP 算法和CO-SAMP 算法的信道冲激响应（channel impulse response，CIR）恢复结果，此时的信道稀疏度设置为5.在图1 中，对于真实的抽头位置11，12，13和17，OMP 算法的系数估计值与CO-OMP 算法的系数估计值基本一致，且能量较大的路径增益系数与真实值比较接近.观察错误抽头位置，OMP 在错误抽头位置60 上的估计值远大于真实信道抽头14 上的系数.而CO-OMP 在错误位置87 上的系数估计值远远小于OMP 在错误位置60 上的系数估计值.由此可见，COS 可以在几乎不影响真实抽头位置上系数估计的同时，有效地抑制错误位置上的系数过估计.由图2 可知，SAMP 算法和COSAMP 算法之间也有着相同的结论.另外，SAMP 算法通过比较残差能量与基于理想信道噪声能量估计的大小来判断何时停止迭代，这减少了低信噪比下抽头错误估计的可能性.COS进一步优化了SAMP 的系数估计结果，使得正确位置11和12上的系数估计值更加接近真实值，从而使得CO-SAMP 具有更高的稀疏恢复性能.

图1 OMP和CO-OMP的信道冲激响应恢复比较（SNR=7 dB）Fig.1 Comparison of channel impulse response recovery between OMP and CO-OMP under SNR=7 dB

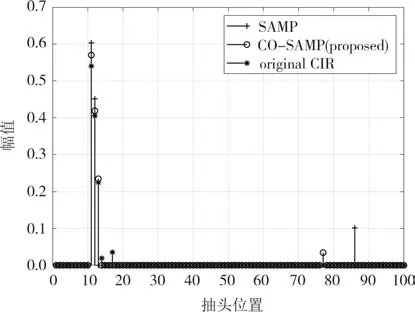
图2 SAMP和CO-SAMP的信道冲激响应恢复比较（SNR=7 dB）Fig.2 Comparison of channel impulse response recovery between SAMP and CO-SAMP under SNR=7 dB

图3～图5 分别展示了OMP、CO-OMP、SAMP 和CO-SAMP 在不同信道模型下的NMSE 性能.为了体现稀疏恢复算法的优势，本文还使用了所有子载波都放置导频下的LS 算法的估计性能作为对比.由图可知，OMP 和SAMP 等稀疏恢复算法比全导频下的LS 算法具有更好的NSME 估计性能，且导频的开销远小于后者.SAMP 算法因为其基于理想的信道噪声能量估计的迭代停止条件，减少了信道噪声对抽头选择的干扰.同时，每次迭代对已选原子的裁剪优化，使得SAMP 算法具有比OMP 算法更优秀的稀疏恢复性能.但是，当信道噪声估计存在偏差时，会较大地影响SAMP 算法和CO-SAMP 算法的性能.COS抑制了信道抽头估计结果中错误原子分量上系数过高的问题，使得所估计的信道冲激响应更接近真实值.观察分析图3～图5 可知，CO-OMP 与CO-SAMP稀疏信道估计系数优化方案分别比OMP 与SAMP 具有明显的NMSE 性能提升，且在低SNR 的时候具有2～3 dB 的提升.即使是基于非理想的信道噪声能量的SAMP 算法，COS 也可以为其带来可观的性能提升.同时随着SNR 的逐渐增大，COS 带来的NMSE 性能提升也随之减小.这是因为SNR 越大，OMP 与SAMP 在抽头位置估计阶段出错的概率越小.COS 旨在减弱错误原子对稀疏信号估计的影响，因此COS在高SNR 处的性能提升相对较小.由此可见，COS 的引入可以提高稀疏信道估计的抗随机噪声的能力.

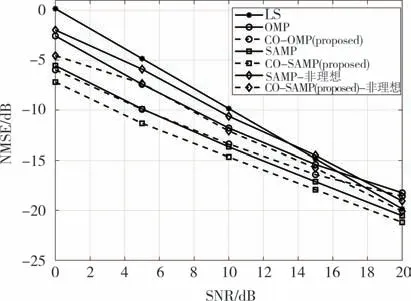
图3 EPA信道模型下的NMSE性能比较Fig.3 NMSE performance comparisons in EPA channel model

图4 EVA信道模型下的NMSE性能比较Fig.4 NMSE performance comparisons in EVA channel model

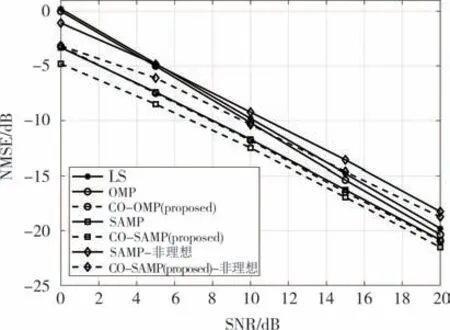
图5 随机多路径信道模型下的NMSE性能比较Fig.5 NMSE performance comparisons in random multipath channel model

考虑到COS 中参与单次LS 运算的原子个数约为信道的稀疏度S并远小于信道的长度L与导频个数M，因此COS 的复杂度O(MS+MS2+S3)相对于以OMP 算法为例的复杂度O(SML)几乎可以忽略不计［16］.

5 结论

本文针对多径信道下OFDM 稀疏信道估计的问题，提出了一种适用于贪婪算法的系数优化方案.该方案通过利用相邻OFDM 符号信道之间时延估计的相关特性，抑制了错误抽头位置上信道系数的过高估计.因此，它自适应地提高了稀疏信道估计对噪声的鲁棒性.实验结果表明，与传统的贪婪追踪算法相比，使用了该系数优化方案的算法在稀疏恢复性能上均有一定的提升，特别是在低信噪比情况下具有更强的抗噪声能力.