基于多维度精确定位的测绘数据处理技术研究

刘锋

（西安铁路职业技术学院，陕西 西安 710026）

传统卫星测绘定位方法的精度较差，当地形结构相对复杂时，其信号便会被遮挡，从而导致卫星无法定位。因此，基于卫星定位功能部署多个无线传感器网络（Wireless Sensor Networks,WSN）[1-3]是改善测绘卫星信号被遮挡的方式之一。目前无线传感器的定位方法可分为两种，第一种方法需要计算各无线传感器间的实际距离，该算法较为准确，但普适性较差，且需要极高的部署成本，故不适合用作大范围区域的无线定位。第二种方法无需计算传感器距离，仅通过无线拓扑的信息传递关系便可对位置进行估算，该方法虽然准确度略逊于第一种，但成本更低且总体上也能取得良好的效果，其代表性算法为3DDV-Hop[4-5]。

由于传统3DDV-Hop算法的定位精度较差，因此为了提升其精度，国内诸多学者均对该算法进行了改进。改进主要分为两个方向：1）对各个传感器节点的最小跳数[6]与平均跳距[7]进行修订；2）通过智能优化算法[8]对节点的位置进行特征学习和估算。文献[9]利用人工蜂群（Artificial Bee Colony,ABC）算法对搜索空间的距离加以改进，并提高了测距精度。但其迭代步数较多，故仍有提升空间。文献[10]则通过概率统计值对节点的位置进行优化及预估，其算法精度虽较高，但计算量也在增大。

该文分析了3DDV-Hop 存在的问题，并从最小跳数、平均跳距及定位坐标的确定方法三方面对算法进行了优化，并在实验部分取得了较优的效果。

1 基于改进3DDV-Hop 的精确定位算法

1.1 3DDV-Hop定位算法

近年来无线传感网络技术发展迅速，定位空间的维度已从二维扩展至三维。而3DDV-Hop 算法作为立体空间中的目标定位方法，受到了广泛关注。传统3DDV-Hop 算法的实现步骤如下：

1）三维空间中的不同节点间，以信息传播的方式确定跳数值。锚节点会发送包含自身标识、跳数值与坐标值的信息包至三维监测区域中的相邻节点，而该节点则会对信息包中的信息进行存储，此后再继续转发给下一相邻节点。以此类推，在监测的三维区域空间中不同节点间以洪泛的形式进行传播，直至整个监测区域内的所有节点均完成信息的传播与存储为止。具体的节点信息传播图如图1 所示。其中白色代表未知节点，黑色则代表锚节点。

图1 三维空间中节点信息传播图

2）以跳数为依据求取平均的跳距值与距离信息。通过步骤1）可知，每个锚节点的路由信息表中，均存储了除去自身以外其他锚节点的坐标值及路由最小跳数值。以每个锚节点记录的信息为依据，可计算整个监测区域的平均跳距值为：

式中，HopSizei表示为整个监测区域的平均跳距，(xi,yi,zi)和（xj,yj,zj）分别为监测区域中两个不同锚节点的坐标信息值，hij则表示上述两个锚节点间的最小跳数值。根据求得的平均跳距值，可计算区域中两个锚节点间的估计距离dij为：

3）区域内未知节点的坐标值计算。通过步骤1）-2），可求得任意未知节点与区域内每个锚节点的距离。以此为基础，并假设在监测区域中每个未知节点均存在至少4 个连通的锚节点，则可采用极大似然估计法（Maximum Likelihood Estimate,MLE）求得未知节点的坐标信息，具体计算过程如下：

其中，(x,y,z)代表的是区域内未知节点的坐标，而(xk,yk,zk)代表的则是区域内与未知节点连通的第k个锚节点坐标，且1＜k＜n。将式（3）转换为矩阵形式PX=Q，则有：

上式中，若存在矩阵A和B使得ATA为可逆矩阵时，则可将区域内未知节点坐标表示为：

1.2 3DDV-Hop定位算法存在的问题

由以上分析可知，利用3DDV-Hop 算法定位的重点是跳数与平均跳距的乘积。通过该值可获取传感器节点的距离，并在测出距离后计算各节点的位置坐标。

计算跳数时，在通信半径内的所有覆盖节点均会记为一跳，由此便会造成统计错误。同时在多个通信半径内的节点通信路径并非直线，这样需经过多次跳数才能完成通信。此外在求解节点位置时，通常使用三边定位法（Trilateral Positioning Method）来完成。但当三个节点在一条直线时，三边定位法就会失效。因此，影响3DDV-Hop 精度的主要原因有三个：跳数、平均跳距及节点坐标计算方法。

1.3 算法改进

1.3.1 基于双通信半径法的最小跳数修正

传统的跳数计算[11]方式使用单通信半径法，但该方法的误差较大。因此为了减小误差，该文使用双通信半径法对最小跳数进行修正[12]。双通信半径算法的示意图如图2 所示。

假定节点数据传输共有R和0.5R这两种传输半径，且锚点A分别在传输半径R与0.5R处传输信息，由此测得的数据将会更加精确。从图中可以看到，节点1、2 在0.5R半径内，故这两个节点的跳数均为0.5，而节点3、4 的跳数则为1。这使得拓扑更具真实性，也是提高定位精度的前提。

1.3.2 加权平均跳距改进方法

由式（2）可知，使用单一代价函数计算得到的值会存在一定误差。因此，该文采用平方代价函数对单一函数进行改进。其可表示为：

由偏导数可求解得到HopSizei的值如下所示：

式（8）-（9）为单个节点与其他节点的平均跳距，且当这两个数值间的跳距相差较小时，就会引起误差。因此，可以使用多个节点的加权值对精度进行提升，但节点过多会导致计算量激增。同时，若两个节点相距过远，对最终的结果影响也较小。所以选择单个节点及与其距离最近三个节点的跳距平均值作为加权值，计算公式如下：

式中，Ni、Nj、Nk为某锚节点与其距离最近节点i、j、k的最小跳数值。节点α加权后的跳距可表示为：

1.3.3 最小最大节点坐标计算法

在坐标求解中，使用最小最大法（Min-Max）[13]对最终坐标进行求解。该方法使用求解完成的锚点坐标与计算完毕的跳距值，在空间中构建最小与最大区域限制函数。再通过计算各个限制函数所构成的限制圆质心求得坐标值。其在提升精确度的同时，还可减小了一定的计算量。Min-Max 算法的构造如图3 所示。

图3 Min-Max算法构造

图3 中，A、B、C是离位置节点D最近的三个锚节点，且节点间的距离是已知的。A、B、C的节点坐标为(xp,yp,zp)(p=A,B,C)，则锚点限制区域如下所示：

式中，下限值的最大与最小值为各区域的交集，而这些交集所形成的图形质心则为未知锚点的坐标值。

1.3.4 改进算法流程

该文对影响3DDV-Hop 定位算法精度的因素进行了改进[14]，算法的执行流程如下：

1）定位节点初始化。由空间中的定位节点构建定位系统，且初始化的最大通信半径为R，节点总数为P。

2）双通信半径传播。根据双通信半径法设定R和0.5R的传播半径进行最小跳数修正，直至网络中锚节点数据传播完成为止。

3）计算平均跳距。依据加权法（Weighting Method）对锚点间的平均跳距加以计算，并选择与未知节点距离最近的三个节点进行加权。

4）计算最终坐标。使用Min-Max 算法构建限制区域，同时计算上下限区域的质心，以得到未知节点的坐标，进而完成最终定位。

2 算法测试

2.1 实验平台

文中使用Matlab[15-16]对测绘空间数据进行生成与仿真。利用部署于测绘空间内部的锚节点个数、通信半径及未知节点个数三方面进行算法性能的对比。所构建的仿真实验环境如表1 所示。

表1 实验环境

2.2 实验测试

文中利用上述三方面的变化值对算法性能加以测试。选取了3D-DVHop、3D-WD-DVHop 及IPSODV-Hop 这三种经典算法来与所提方法进行对比。所使用的参数指标则为误差距离，即测量值和实际值之间的欧式距离（Euclidean distance）。默认的实验环境：200 个传感器，20%的锚节点，80%的未知网络节点，同时通信半径为35 m，且做50 次实验后取平均值[17-18]。

验证通信半径对定位精度的影响，取25～60 m之内的通信半径，并测量定位误差，所得结果如图4所示。

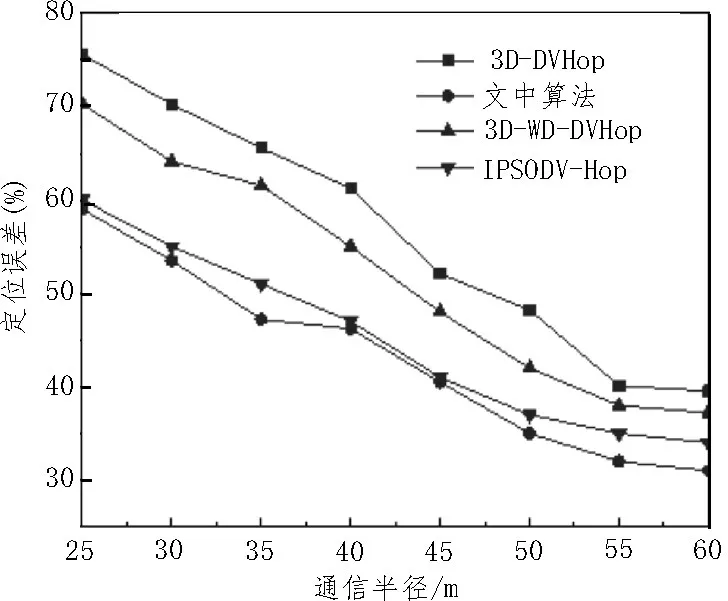
图4 通信半径对定位精度的影响

由图可知，随着通信半径的增大，锚节点可以覆盖更多的通信节点，因此误差也逐渐降低。此外该算法在对比算法中具有最低的误差值，且相较IPSODV-Hop 算法误差降低了2.1%。

除了通信半径以外，锚节点个数对定位误差也有较大的影响。当锚节点个数取10～40 个时，各算法的结果如图5 所示。

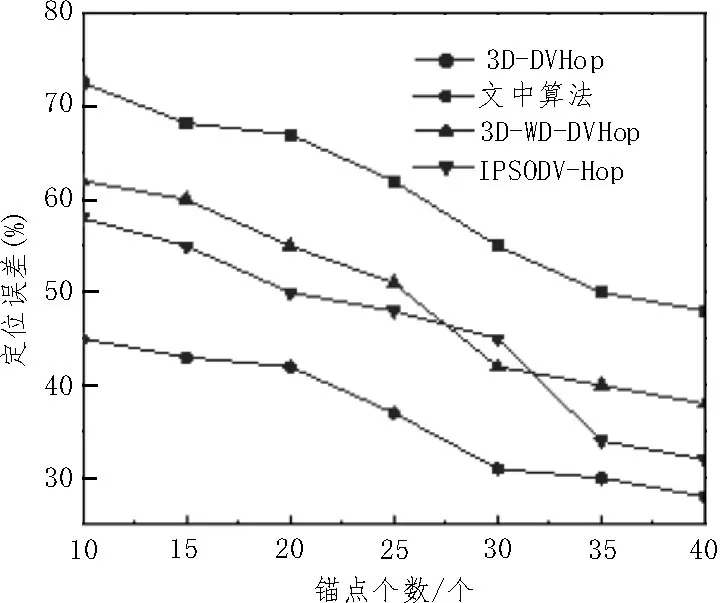
图5 锚点个数对定位精度的影响

从图中可看到，在锚节点数量较少时，各算法误差均较大。而随着锚节点数量的增加，各算法的误差均有所下降。由于该算法对跳距与跳数进行了优化，因此其定位误差的平均值比其余三种算法的平均值下降了约6.8%。

此外，未知节点总数对网络的连通性也有直接的影响。文中在节点数量为125～275 个之间进行了仿真，所得结果如图6 所示。

图6 节点数量对定位精度的影响

由图6 可知，在节点数量较少时，由于网络的连通性较差，所以其定位误差较高。而随着节点个数的增加，定位误差也随之下降。而该算法通过增加节点半径来对节点数量的不足加以补偿，比其他三种算法的定位误差平均值降低了约5.4%。

综上所述，该算法通过对最小跳数、跳距及定位算法进行了优化，其综合性能较为理想，定位精度相较对比算法也有所提升。

3 结束语

传统卫星测绘算法定位精度较差，该文针对算法存在的三个缺陷进行了改进。分别使用双通信半径法、加权平均法和最小最大法对算法进行了优化。实验测试结果显示，所提算法误差指标在对比算法中均为最优，表明该算法可以有效提升卫星测绘的精确度。