基于BP神经网络优化的卡尔曼滤波算法在轨道垂向不平顺估计中的应用

彭浪　梁树林　池茂儒

摘要：轨道不平顺是引起车辆和轨道振动的主要原因，也是影响列车平稳性和舒适性的关键因素。本文根据卡尔曼滤波（KF）最优估计原理，建立了车辆系统模型，通过观测车辆系统中车体、前后构架的多个惯性量，采用BP神经网络优化卡尔曼滤波（BP-KF），实现了轨道垂向不平顺的估计。结果表明，优化后的轨道垂向不平顺估计值，无论是在趋势上还是幅值上与原始值都具有较高的一致性，为轨道不平顺的间接估计提供了新的技术手段。

关键词：铁道车辆；轨道不平顺；卡尔曼滤波器；BP神经网络

中图分类号：U279.2 文献标志码：A doi：10.3969/j.issn.1006-0316.2023.05.010

文章编号：1006-0316 （2023） 05-0058-07

Application of Kalman Filter Algorithm Based on BP Neural Network Optimization

in the Prediction of Vertical Track Irregularity

PENG Lang，LIANG Shulin，CHI Maoru

（ State Key Laboratory of Traction Power， Southwest Jiaotong University， Chengdu 610031， China ）

Abstract：Track irregularity is an important excitation source of vehicle and track vibration， and also a key factor affecting train ride and comfort. Based on the principle of Kalman filter （KF）， a vehicle system model is established in this paper. By observing several inertial quantities of the vehicle system， the optimal estimation principle of Kalman filter is used to estimate the vertical irregularity of the track. Finally， BP neural network is used to optimize the Kalman filter. The results show that the optimized vertical irregularity estimates have a high consistency with the original values both in trend and amplitude， which provides a new technical method for the indirect estimation of track irregularity.

Key words：railway vehicle；track irregularity；Kalman filter；BP neural network

列車运行的安全性和平稳性，受到线路条件的直接影响，而轨道不平顺是引起车辆和轨道振动的主要原因。轨道不平顺的检测，能够检查出轨道的质量状态，在保证列车运行的平稳性和安全性、维护轨道等方面有着重要的工程价值。目前，国内外对轨道不平顺的检测手段主要包括直接法和间接法。

直接法是采用人工、轨检小车、大型综合轨道检查车。人工检测和轨检小车依赖于操作者的专业技术，检测误差难以保障，且耗时长、效率低；大型综合轨检车克服了这些缺点，但造价高、维护成本高、无法检测出铁路系统的所有线路情况。

针对轨道不平顺直接检测方法的缺陷，国内外诸多学者提出了轨道不平顺的间接检测方法。周佳亮[1]提出一种基于车轨耦合动力学的轨道不平顺估计算法，以遗传算法对轨道动态不平顺进行估计，并结合无迹卡尔曼对估计偏差进行最优滤波，轨道谱最终估计结果与实测值有较高相关性。Lee等[2-3]建立构架状态空间模型，利用卡尔曼滤波技术对构架振动响应进行分析，实现轨道不平顺反演估计，虽然该方法能同时估计出横向和垂向轨道不平顺，但是估计结果与真实值存在一定差异。Alfi S等[4]提出一种轨道长波不平顺识别方法，通过测量包括车体、转向架等部件的振动响应来进行识别，该方法将轨道看作刚性系统，忽略了轨道的柔性和非线性的轮轨接触关系，与实际情况存在较大差异。

陈岳剑[5]研究了基于积分、带通滤波和自适应的轨道不平顺在线监测法，实现轨道垂向不平顺检测，同时使用于扩展卡尔曼滤波理论，提高了垂向不平顺检测的精度。Kawasaki等[6]建立车辆仿真模型，获得车辆的振动加速度数据，再通过一个输入为车辆加速度、输出为轨道不平顺的反向模型来进行辨识，仿真分析表明，车辆的质量和运行速度对估计的结果有较大影响。Song Liu等[7]提出一种使用神经网络来估计轨道不平顺的方法，通过车体加速度得到了轨道不平顺的估计值。Li MXD[8-9]提出一种车轨耦合的动力学模型，在时域中构建基于系统辨识的滤波器函数求解动力学模型，而后利用输入输出数据建立轨道不平顺的反演模型，实现垂向轨道几何状态的评估。

本文建立了整车动力学模型，采用BP（Back Propagation，反向传播）神经网络优化的卡尔曼滤波算法（Kalman Filter，FK），在仿真环境下研究轨道垂向不平顺估计技术。

1 基于BP神经网络优化的卡尔曼滤波估计轨道垂向不平顺

首先通过车辆系统的动力学方程得到该系统的状态空间方程和观测方程，再经过卡尔曼滤波算法得到轨道垂向不平顺的最优估计值，最后针对卡尔曼滤波估计的误差，将影响卡尔曼滤波估计的参数作为BP神经网络的输入，轨道不平顺的原始值与最优估计值的残差作为输出，经过神经网络修正得到新的轨道垂向不平顺估计值。

1.1 整车动力学系统的卡尔曼滤波模型

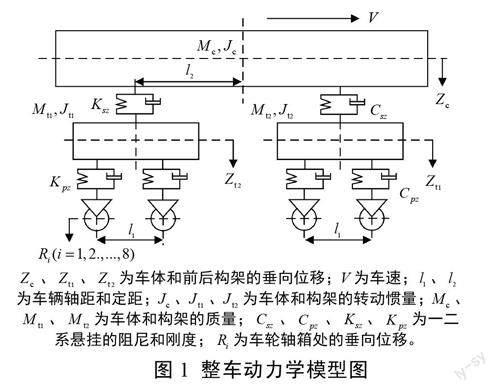
根据轨道车辆的动力学特点，考虑轨道车辆运行过程中，垂向运动和横向运动二者的弱耦合性特点，忽略车辆的横移和摇头自由度的影响。考虑到轮轨力无法直接获得，轨道垂向不平顺简化近似看做轴箱的垂向位移，最终建立如图1所示的整车动力学模型，模型中共计17个自由度，包括车体、前后构架的浮沉、点头及侧滚自由度，以及轴箱的浮沉自由度。

车辆系统的动力学方程可描述为：

设置网络最大迭代次数1000，学习率0.01，系统训练选择L-M算法，trainlm训练函数。

2 仿真与分析

采用上述BP-KF算法进行仿真分析，首先通过整车动力学模型得到卡尔曼滤波算法的系统状态方程和观测方程、车辆系统的状态响应量的仿真值，再通过式（11）～（18）得到轨道不平顺的最优估计值，其中KF算法滤波参数设置为系统初始状态量x0＝[0]34×1，初始协方差P0＝I34×34，过程噪声矩阵Q＝I34×34，测量噪声矩阵R＝I9×9，最后将最优估计和卡尔曼增益等滤波参数按照图5更新最优估计，得到的新的轨道不平顺估计值。

左右轨轨道不平顺估计值如图6所示，可以看出，BP-KF算法估计值比KF算法估计值更加接近轨道不平顺的原始值。由图7可以看出，BP-KF算法在轨道不平顺幅度上也与原始值有较高的一致性。

为进一步量化两种算法的估计值和原始值之间的逼近程度，计算了两种算法的估计值与原始值之间的均方根误差和相关系数。

左右轨轨道不平顺估计值均方根误差如图8所示。可以看出，BP-KF算法的均方根误差明显低于KF算法。KF算法的左右轨不平顺估计值均方根误差均值分别为1.7921×10-2 mm、2.4715×10-2 mm，BP-KF算法左右轨不平顺估计值均方根误差均值分别为1.5202×10-2 mm、2.0146×10-2 mm。说明BP-KF算法的精度更高。

两种算法的轨道不平顺估计值与原始值的相关系数如表1所示，BP-KF算法的相关系数明显大于KF算法的，处于0.8～0.9之间，属于强相关关系。

综上所述，BP-KF算法估计的轨道垂向不平顺在趋势和幅值上与原始值有较高一致性。再从相关系数和轨道不平顺估计值均方根误差可知，BP-KF算法提高了KF算法的精度。验证了BP-KF算法的轨道不平顺的可行性。

3 结论

本文提出一种基于BP神经网络优化的卡尔曼滤波算法用于轨道垂向不平顺估计，建立了整车轨道不平顺估计模型。仿真结果表明，经过BP神经网络优化后的卡尔曼滤波算法对轨道垂向不平顺估计值，无论是在趋势还是幅值上与原始值都具有较高的一致性，同时在精度上也高于经典的卡尔曼滤波算法。验证了BP神经网络优化的卡尔曼滤波算法在轨道垂向不平顺估计中的可行性、鲁棒性。

参考文献：

[1]周佳亮. 基于车辆－轨道垂向耦合模型的轨道不平顺估计[D]. 北京：北京交通大学，2011.

[2]LEE J，CHOI S，KIM S，et al. Estimation of rail Irregularity by Axle-Box Accelerometers on a High-Speed Train[J]. Noise and Vibration Mitigation for Rail Transportation Systems，2012（118）：571-578.

[3]LEE J，CHOI S，KIM S，et al. A mixed filtering approach for track condition monitoring using accelerometers on the axle box and bogie[J]. IEEE Transactions on Instrumentation and Measurement，2012，61（3）：749-758.

[4]Alfi S，Bruni S. Estimation of long wavelength track irregularities from on board measurement[C]. Stevenage， UK：4th IET International Conference on Railway Condition Monitoring RCM 2008，IET，2008.

[5]陈岳剑. 车辆轨道耦合建模与轨道不平顺在线惯性监测研究[D]. 南京：南京理工大学，2015.

[6]KAWASAKI J，YOUCEF-TOUMI K. Estimation of rail irregularities[C]. Anchorage， AK：Proceedings of the 2002 American Control Conference （IEEE Cat. No. CH37301），2002（5）：3650-3660.

[7]Song Liu，Xuemiao Pang etc. Prediction of track irregularities using NARX neural network[C]. Proceedings of 2010 Second Pacific-Asia Conference on Circuits，2010（1）：109-112.

[8]Li MXD．Berggren EG，Berg M，et al. Assessing track geometry quality based on wavelength spectra and track-vehicle dynamic interaction[J]. Vehicle System Dynamics，2008，46（suppl1）：261-76.

[9]Li MXD．Berggren EG，Berg M. Assessment of vertical track geometry quality based on simulations of dynamic track-vehicle interaction[C]. London：Professional Engineering Publishing Ltd.，2009.

[10]范佳靜，曹玉华，曹敏. 基于GABP神经网络预测法的工程机械再制造员工效率研究[J]. 工业技术经济，2018，37（8）：147-153.

[11]曹浏. 基于BP优化的卡尔曼滤波算法在行人跟踪中的应用[D]. 西安：西安理工大学，2021.

[12]于耕，方鸿涛. 基于BP神经网络改进UKF的组合导航算法[J]. 电子技术应用，2019，45（4）：29-33.