轴流式机组轴系临界转速分析及优化

陈仲章　陈学标　林真　于昊楠　王云鹤　肖惠民

摘要：水轮发电机组轴系的动力特性和稳定性关系到机组的安全稳定运行。为研究某大型立式轴流式机组轴系的自振特性，防止轴系因振动而损坏，采用转子动力学计算方法，建立了轴系的三维有限元模型，计算分析了机组轴系的临界转速特性。计算结果表明，因原有轴系刚度不足，导致一阶临界转速小于机组飞逸转速，轴系有可能出现共振，需对轴系进行优化。针对此情况提出提高轴系材料刚度和增加下导轴承两种优化方案。有限元计算表明，提高轴系材料刚度后机组一阶临界转速依然小于飞逸转速，不满足刚性转子的要求；而增加下导轴承可大幅提高一阶临界转速，对提升轴系运行稳定性有明显效果。

关键词：立式轴流式机组；转子动力学；轴系；临界转速；导轴承

中图分类号：TV734.1 文献标志码：A doi：10.3969/j.issn.1006-0316.2023.05.006

文章编号：1006-0316 （2023） 05-0035-05

Analysis and Optimization of Critical Speed of Axial Flow Unit Shafting

CHEN Zhongzhang1，CHEN Xuebiao1，LIN Zhen1，YU Haonan2，WANG Yunhe2，XIAO Huimin2

（ 1.Youxi Basin Branch of Fujian Shuikou Power Generation Group Co.， Ltd.， Youxi 365100， China; 2.School of Power and Mechanical Engineering， Wuhan University， Wuhan 430072， China ）

Abstract：The dynamic characteristics and stability of the shaft system of a hydro generator set are related to the safe and stable operation of the set. In order to study the self-vibration characteristics of the shaft system of a large vertical axial turbine and prevent the damage of the shaft system due to vibration， through the calculation method of rotor dynamics， a three-dimensional finite element model of shafting is established， and the critical speed characteristics of shafting are calculated and analyzed. The calculation results show that the first-order critical speed is less than the flyaway speed due to the insufficient stiffness of the original shaft system. The shafting may have resonance， so it is necessary to optimize the shafting. Two optimization schemes of increasing the material stiffness of the shafting and increasing the lower guide bearing are proposed. The finite element calculation shows that the first critical speed of the unit is still lower than the flyaway speed after the material stiffness is increased， which does not meet the requirements of rigid rotors. But adding the lower guide bearing can significantly increase the first-order critical speed and has a significant effect on improving the stable operation of the shaft system.

Key words：vertical axial flow unit；rotor dynamics；shafting；critical speed；guide bearing

水輪发电机组是水电站核心设备，随着科学进步和在设计制造方面不断突破，机组的容量、尺寸和功率不断提升，集成化程度也不断提高。在水力、机械、电气等复杂因素作用下，尤其当水压力脉动、质量偏心等激励力频率与轴系临界转速对应的频率重合时，轴系会出现剧烈的振动，危及到机组的安全稳定运行。由此可以看出，水轮发电机组在运行过程中的安全和稳定与轴系的临界转速紧密相关，所以对轴系的临界转速特性分析至关重要。

水轮发电机组临界转速分析是一个多种因素耦合的复杂转子动力学问题，其发展经历了从一维到三维、从刚性支撑到考虑轴承和支座的弹性支撑，从传递矩阵法到有限元法，计算精度不断提高[1-5]。

对轴系临界转速的计算分析，马震岳等[6]分析了轴系临界转速对大轴尺寸、导轴承数目及几何布置、不平衡力等因素的敏感度分析，从而得出各因素的影响程度；白冰等[7]通过改变导轴承刚度系数，研究了各导轴承对轴系临界转速的影响；李国慧等[8]对某高转速水轮发电机组临界转速进行了系统性分析，研究了陀螺效应对机组轴系统弓状回旋自振特性的影响；徐瑞红等[9]建立了轴系有限元模型并对各阶临界转速和模态进行对比；王正伟等[10]对轴系在不同工况下的临界转速进行了分析计算。

本文以某大型立式轴流式机组轴系为研究对象，运用转子动力学计算方法，使用ANSYS有限元分析软件，建立轴系三维仿真模型，计算原有轴系临界转速。再根据原有轴系临界转速的分布特点，通过增加轴系刚度和增加下导轴承两种方法进行优化，并将优化结果与原有轴系临界转速进行对比，验证优化效果。

1 转子动力学计算方法

转子动力学主要针对转子的横向弯曲振动问题，建立模型并对转子的临界转速、振型、不平衡响应和稳定性等方面进行系统性的研究，为减小转子振动、转子动力优化设计、提高转动机械寿命和运行稳定性提供理论支持。

转子动力学方程由结构动力学方程演化而来，根据水轮发电机组的实际运行特点，其运动方程一般可写为：

式中： 、 、 为质量矩阵、阻尼矩阵和刚度矩阵，三者为实对称矩阵； 为回转矩阵，因转子系统具有陀螺效应，矩阵为实反对称矩阵； 为机组转速； 、 和 分别为广义位移、速度和加速度向量； 为载荷向量，代表作用在系统上的广义外力。

在计算机组的临界转速时，需将式（1）转化为齐次式进行研究，即令 ＝0，则式（1）可写为：

目前求解转子动力学问题的主要方法为传递矩阵法和有限元法两种。本文采用有限元法進行求解，因所研究分析的模型较大、自由度多，使用有限元法比传递矩阵法计算精度更高、操作更简单，并且可以将研究对象的分析结果以清晰的图表方式呈现。

2 机组轴系临界转速计算

2.1 机组轴系参数

机组水轮机为轴流式水轮机，发电机为半伞式，设有上导轴承和水导轴承，轴系的转速、重量及材料参数如表1所示。

2.2 轴系模型的建立及分析设置

建立合理的几何模型对于准确进行结构动力学分析至关重要，本文所建立的轴系三维模型如图1所示，包含转动系统（从上到下依次为顶轴、发电机转子、发电机轴、水轮机轴及水轮机转轮）和支撑系统（上导轴承及水导轴承轴领）。支撑系统为转动系统的边界条件，因不考虑轴系的纵向支撑情况，所以对上下机架及推力轴承进行了忽略，上导轴承、水导轴承的轴领作为边界条件的设置对象进行了保留，原轴系不含下导轴承。

将建立的轴系模型进行整体有限元划分，网格类型采用四面体网格，单元长度200 mm，根据设置共划分出115469个单元网格，有限元网格划分情况如图2所示。

在约束上对轴系Z轴方向上进行设置，使其不发生轴向位移；上导轴承刚度系数与水导轴承相同，均设置为2.0×109 N/m；对轴系转速范围及间隔进行设置，本研究中轴系转速范围在100～800 r/min，转速间隔为100 r/min。

2.3 临界转速计算结果

根据如上轴系模型建立及分析设置，对轴系进行临界转速计算，得到图3。

坎贝尔图反映了激励转速与固有频率间的关系，其中，激励转速代表转动系统的实际转动速度，固有频率代表转动系统的动力学特性。绘制各激励转速与该转速下固有频率的关系线，即各阶模态的计算线（Mode_1～Mode_6）；绘制固有频率与激励转速之比的直线，二者的交点即为轴系的临界转速。根据轴系坎贝尔图得到的轴系前六阶临界转速如表2所示。

与前三阶临界转速对应的轴系振型情况如图4所示。可以看出，在一阶临界转速下，轴系在发电机转子处的摆动处于最大值，而在二阶和三阶临界转速下，轴系在水轮机转轮处的摆动处于最大值。

分析轴系在运行过程中是否稳定，需要将一阶临界转速与轴系的飞逸转速进行对比分析。保证轴系的一阶临界转速大于飞逸转速。该机组轴系一阶临界转速为154.91 r/min，飞逸转速为210 r/min，一阶临界转速小于飞逸转速。那么，在该机组的运行过程中，有可能出现轴系共振，所以有必要对轴系进行优化。

3 轴系临界转速优化

对于本文所研究的轴系，可以从提高轴系刚度入手优化临界转速，可行措施有：①通过提高材料的弹性模量，直接提高轴系的刚强度；②与其他多数轴流式轴系相比，该轴系因缺少下导轴承，使得上导轴承和水导轴承之间的距离过长，法兰处缺乏支撑导致此处摆度过大，因此可通过增加下导轴承来提升轴系刚度。

3.1 提升材料刚度

将材料的弹性模型从2×105 MPa提高到2.4×105 MPa，提高轴系的刚强度。仿真计算时，其他约束设置和受力情况与原轴系相同。

对提升材料刚度后的轴系进行临界转速计算，得到坎贝尔图如图5所示。

由图5可以得到增加轴系刚度后轴系转动系统前五阶的临界转速情况，如表3所示。

提高轴系刚度后，轴系的一阶临界转速为158.13 r/min，有少许提高，介于机组额定转速71.4 r/min与飞逸转速210 r/min之间。如果与额定转速相比，则机组轴系为刚性转子；如果与飞逸转速相比，材料刚强度提高20%后，一阶临界转速依然低于飞逸转速，不满足刚性转子的要求。虽然继续提高轴系刚度可进一步提高一阶临界转速，但不经济。

3.2 增加下导轴承

参照电厂内其他机组构造情况，在推力头外侧加装下导轴承，轴瓦中心线与转子中心线相距约1.2 m。

对下导轴承设置与上导、水导轴承相同的刚度系统和约束，对改造后的轴系进行临界转速计算，得到的坎贝尔图如图6所示。

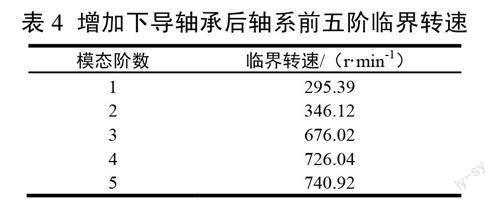
由图6可以得到增加下导轴承后轴系转动系统前五阶的临界转速，如表4所示。

增加下导轴承后，轴系临界转速有大幅提升，重点关注的轴系的一阶临界转速增大到295.39 r/min，已远离机组飞逸转速210 r/min。即，增加下导轴承后，一阶临界转速远高于额定及飞逸转速，轴系可安全运行。

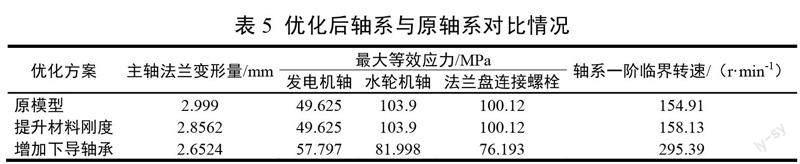
优化后轴系与原轴系的摆度、应力和一阶临界转速对比情况如表5所示。可以看出，增加下导轴承后，能明显减小主轴的法兰变形量，增加转动系统的一阶临界转速，对于可能发生的共振和主轴法兰摆度偏大的问题改善明显。提升材料刚度的改善效果不显著。

4 结语

本文以某大型立式轴流式机组轴系为研究对象，针对轴系临界转速问题进行分析与结构优化，得到结论如下：

（1）原有轴系一阶临界转速大于额定转速但小于飞逸转速，轴系在运行过程中可能出现共振，需要进行改造；

（2）提高轴系刚度对增加临界转速效果有限，不足以达到稳定运行要求；

（3）对原轴系增加下导轴承，可以明显提升轴系一阶临界转速，已远离机组飞逸转速，有效提高了轴系安全稳定运行的范围；同时在相同激励的情况下，增加下导轴承后主轴法兰处的摆度值明显减小。

参考文献：

[1]顾家柳. 转子动力学[M]. 北京：国防工业出版社，1985.

[2]钟一谔. 转子动力学[M]. 北京：清华大学出版杜，1987.

[3]闻邦椿. 高等转于动力学——理论、技术与应用[M]. 北京：机械工业出版社，2000.

[4]马震岳，董毓新. 水轮发电机组动力学[M]. 大连：大连理工出版社，2003.

[5]王正. 转动机械的转子动力学设计[M]. 北京：清华大学出版社，2015.

[6]马震岳，董毓新. 有限元法分析水电机组轴系的临界转速[J]. 水电站机电技术，1991（4）：5-10，17.

[7]白冰，张立翔，赵磊. 导轴承刚度对水轮机轴系自振特性的影响[J]. 排灌机械工程学报，2013，31（4）：318-324.

[8]李國慧，严锦丽，吴英龙. 某高转速水轮发电机组临界转速分析[J]. 西北水电，2017（4）：23-28.

[9]徐瑞红，龙胜鹏，于凤荣，等. 基于ANSYS水轮发电机组轴系临界转速及模态分析[J]. 云南水力发电，2020，36（2）：103-106.

[10]王正伟，喻疆，方源，等. 大型水轮发电机组转子动力学特性分析[J]. 水力发电学报，2005（4）：62-66.

收稿日期：2022-10-08

基金项目：国网福建省电力有限公司科技项目——基于信息融合与数据挖掘的水电机组故障预警方法研究与应用（5213S2220002）

作者简介：陈仲章（1973－），男，福建尤溪人，工程师，主要从事水电站自动化设备检修维护技术管理工作，E-mail：chenzz298@163.com。*通讯作者：王云鹤（1995－），宁夏银川人，博士，主要研究方向为水电机组健康评价与故障诊断，E-mai：2013301390055@whu.edu.cn。