流固耦合影响下双圆弧斜齿齿轮泵转子力学特性研究

周群起，董庆伟，李阁强，刘理想

（河南科技大学机电工程学院，河南洛阳 471003）

1 引言

外啮合齿轮泵因具有大流量、重量轻、对油液不敏感、结构简单等优点，在航空航天、农耕机械、水力发电等领域被广泛应用。转子是齿轮泵的重要组成部分，传统的齿轮泵的齿轮转子大部分采用的是渐开线齿廓，针对渐开线齿轮泵在工程实际中存在径向力不平衡、转速小、噪声大、压力脉动大、寿命短等缺陷［1］，提出一种过渡曲线以正弦曲线为齿形的双圆弧斜齿齿轮泵。由于该齿轮泵具有压力脉动小、噪音低、效率高、排量大、寿命长等特点，因此，双圆弧斜齿齿轮泵能够在高速高压下稳定工作非常具有研究价值［2］。而转子作为齿轮泵能量传动的重要部件，如何提高稳定性和安全性将对齿轮泵的发展有着深远的影响。

目前，随着有限元软件的发展，流体机械的很多研究方法和理论成果在流固耦合中得以应用；文献［3］使用流固耦合方法为准确获得内部流场及功率损失问题进行研究。文献［4］采用流固耦合方法对内啮合齿轮泵的泵体及其齿轮副受流场的影响情况进行分析；文献［5］使用混流泵内流场和叶轮结构同步求解的方法，研究混流泵叶轮的力学特性。针对上述研究对象大多为内啮合齿轮泵，而对于双圆弧斜齿外啮合齿轮泵这方面的研究较少。因此，构建了Fluent 流体力学和ANSYS运动学相结合的仿真平台，消除单一平台对仿真结果造成的局限性，十分必要。

2 计算结果分析

2.1 物理模型

双圆弧斜齿齿轮泵的转子采用过渡曲线为正弦的双圆弧齿轮作为运动副，点连续接触为该转子啮合方式，由于转子啮合的过程中端面重合度小于1，轴向重合度大于1，因此，齿轮泵具有不产生困油、寿命长、力学特性好等优点。同时理论上这种泵流量连续性好，脉动小，进一步降低了噪声，可以称为“超静音”齿轮泵［6］。双圆弧斜齿齿轮泵组成与结构，如图1所示。

图1 双圆弧斜齿齿轮泵三维模型爆炸图Fig.1 Exploded View of 3D Model of Double Circular Arc Helical Gear Pump

双圆弧斜齿转子啮合所形成的转动副为研究对象，双圆弧斜齿齿轮模型参数，如表1所示。

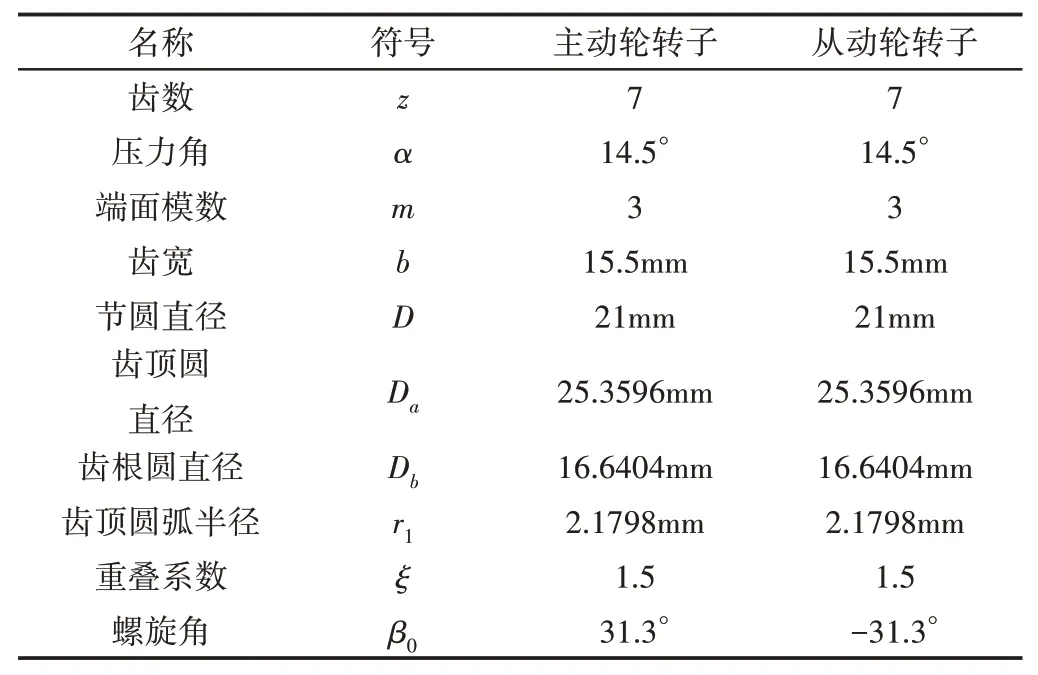
表1 转子模型参数Tab.1 Rotor Model Parameter

2.2 流固耦合基本理论

2.2.1 流体控制方程

双圆弧齿轮泵在Fluent中进行数值计算，需要遵循流体基本守恒定律，其内部流场为粘性不可压缩的非定常流动，其流动控制方程为：

（1）连续性方程：

对于该液压油，可以简化得：

（2）能量方程

Navier−Stokes方程：用于不可压缩流体，可得：

2.2.2 固体控制方程

双圆弧斜齿齿轮泵的泵体和转子假设为刚体，不考虑弹性变形，其方程为：

式中：d—加速度；σ—柯西应力。

2.3 流场计算模型

利用Solidworks 软件对双圆弧斜齿齿轮泵转动副进行三维实体建模，齿轮泵模型转子结构的材料［8］，如表2所示。

表2 转动副参数Tab.2 Rotational Secondary Parameter

2.3.1 流体网格划分

采用ANSYS Space Claim软件构建齿轮泵流域，由于双圆弧斜齿齿轮泵转动副三维模型在数据传输的过程可能存在丢失的问题，通过软件自带的一键修复功能，保证齿轮泵转子模型的完整性。使用软件设置抽取流域的边界条件，将整个流域划分为边界、进油压力、出油压力和主从动轮四个部分。边界条件，如图2所示。

图2 流场计算模型Fig.2 Flow Field Calculation Model

2.3.2 流场计算模型

考虑到齿顶与泵体所形成的间隙对流场的影响较大，为提高间隙内部的网格质量，保证流域计算的精准度和收敛性，因此，在间隙较薄位置采用加密处理，增加单元格层数。在薄壁位置加密方式为独立网格划分（Patch Independent）。与六面体网格划分相比，在相同的精度情况下，四面体的网格单元和节点会更多，采用四面体单元划分网格时，通过设置尺寸控制和边界条件（Proxim⁃ity），控制网格划分精度。网格划分后流域节点约222.7万，单元总数约为1130万，对网格质量不达标的区域进行处理，使处理后网格质量满足Fluent计算需求。

采用Fluent软件进行全流场数值分析，对于双圆弧斜齿齿轮泵，把液压油应看作粘性不可压缩非定常流动（Transient）。设置为绝对速度（Absolute）为求解器速度，采用默认的Standard Wall Functions，计算方法选用隐式求解算法（Implicit）和一阶迎风格式，同时，使用混合动力初始化（Hybrid Initialization）。主从动齿轮的质量中心位置，如表3所示。

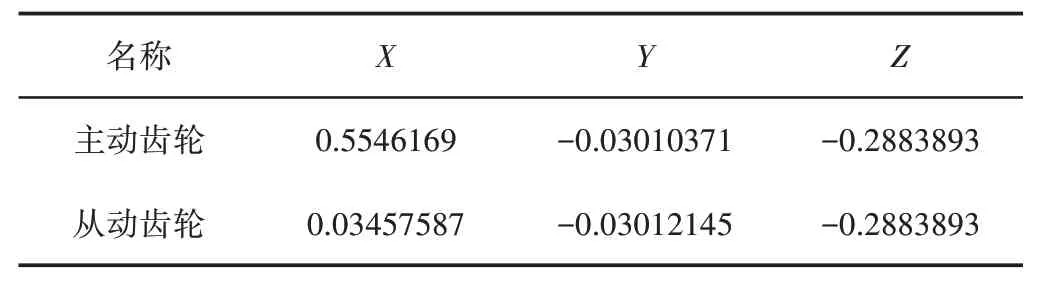
表3 质量中心位置Tab.3 Center of Mass Location

2.3.3 流场计算结果

双圆弧斜齿齿轮泵进口压力为1 个大气压齿、出口压力为25MPa、主动轮和从动轮转数为10000r/min的压力分布，如图3所示。计算收敛精度为10−3。根据图3所示，液体压力在进口边处最低，在靠近转子出口处达到最大，沿着液体流动方向，液体压力逐渐升高。泵体内壁和转子表面之间围成多个相对封闭的体积，体积内的压力值相对稳定，且高压区到低压区到之间的过渡区压力值呈线性递减。

图3 压力云图和啮合处压力云图Fig.3 Pressure Cloud Diagram and Pressure Cloud Diagram at Mesh

由图3可知，在齿轮泵转子啮合位置存在最大压力和最小负压，在进油口转子啮合位置存在最小负压，在出油口转子啮合位置存在最大压力。采用数值计算的方法对转子表面压力进行分析，以实时数据传递的方式，导出流场压力分布载荷［9］。

2.4 转子计算模型

2.4.1 转子有限元网格划分

利用Workbench 中的Mesh 功能进行结构的有限元网格划分，选择独立网格划分方式为四面体（Tetrahedrons），如图4所示。另外流域的坐标与转动副的坐标在各自求解器中保持相同，使流体界面与相接触的结构界面保持对应。

图4 转动副有限元网格模型Fig.4 Finite Element Mesh Model of Rotating Joint

流体计算区域在Fluent 中进行稳态计算，固体结构域在ANSYS Workbench中进行静态动力学分析。在转轴与滑动轴承接触处施加圆柱支撑（Cylindrical Support）约束其径向位移，轴向、切向自由。转动副边界条件，设置进出口压力，进油口处设置最低压力为0.1MPa，出油口处设置最大压力为25MPa，过渡区的压力值由低压区至高压区呈等差分布，如图5所示。

图5 转动副边界条件Fig.5 Boundary Condition of Rotation Joint

2.4.2 有预应力的模态求解结果

转子在分布载荷作用下的变形和应力分析，如图6所示。该结果将作为预应力边界条件对后面的模态进行分析。从图6中可以看到转子变形由中心向外逐渐增大，最大的变形发生在转子近轮缘位置，轴上的变形最小，最大变形量为0.013179mm。由于转子的最大作用力在从动轮上，故从动轮的最大变形量比主动轮要大。转子最小等效应力发生在轴上和靠近轮缘区域，最大等效应力发生在转子齿面啮合位置，最大等效应力为223.15MPa，小于转子材料的屈服强度和疲劳极限，因此齿轮泵转子不会发生塑性变形和疲劳损坏。

图6 转动副应力与变形分布Fig.6 Rotor Pair Stress and Deformation Distribution

将仿真结果作为预应力对转动副模态进行分析，双圆弧斜齿齿轮泵转子模态数据结果，如图7所示。

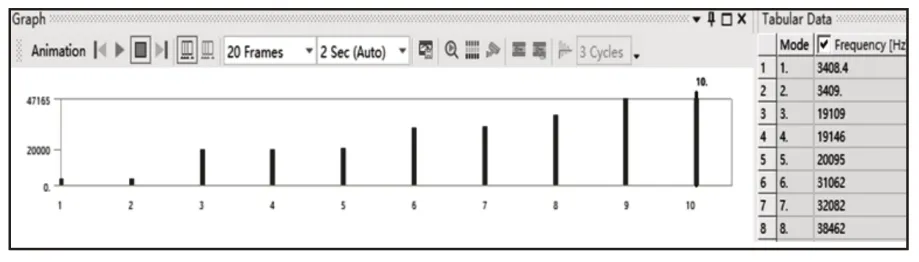
图7 转动副模态分析数据Fig.7 Modal Analysis Data of Rotating Joint

由图7可知，双圆弧斜齿齿轮泵转子第1阶频率3408.4Hz，而齿轮泵通过频率为166.67Hz。由于齿轮泵的通过频率远小于转子自振频率，因此不会发生共振［10］。

2.5 流固耦合计算

将Fluent 分析得到转动副上的分布载荷压力建立数据传递，导入Workbench Structural 中进行压力加载，压力分布，如图8 所示。由前文的分析可知，转子在耦合情况与非耦合情况下，等效应力和最大变形分布区域基本相同。从图9中可以看到齿轮泵转子最大变形量约为0.029242mm，最大的变形发生在转子近轮缘位置，齿轮泵转子轮毂处的小变形，引起转子轮缘处的变形放大，是齿轮泵转子轮缘发生的大变形主要因素。从图a中也可以看出最大等效应力发生在转子啮合附近，最大等效应力约405.87MPa，转子经过周期性应力循环，在截面位置易产生疲劳损坏。

图8 施加压力载荷图Fig.8 Applied Pressure Load Diagram

图9 转动副应力与变形分布Fig.9 Rotating Pair Stress and Deformation Distribution

则此时安全系数为：

式中：σn—许用应力。

最大接触应力处的安全系数大于最小安全系数2.5，所以强度和刚度都满足要求。

在转子外缘部分，其离心力造成的拉伸变形很小，流场压力和转子扭矩造成转子变形较大，由此表明齿轮泵转子的离心力对其影响很小，但流体作用力和扭矩造成的影响比较大。同时，由于最大压力发生在出油口转子啮合位置，最小负压发生于靠近进油口转子啮合位置，当其发生振动时，容易导致转子在轮毂处形成应力集中，成为转子最大等效应力分布区域。

探究流固耦合前后负载对转动副最大变形与最大应力的影响，通过搭建实验测试装置对该齿轮泵进行测试，以验证仿真结果的可靠性，如图10 所示。负载压力（出油口压力）分别为15MPa、20MPa、25MPa和30MPa，转子转速为10000r/min时，分析双圆弧斜齿齿轮泵转动副变化曲线。

图10 试验测试装置Fig.10 Experimental Facility

由图11 可知不同负载下耦合与非耦合结果对比。耦合情况下负载对转子的最大变形和应力影响较为明显，但最大等效应力仍然满足材料疲劳极限和屈服强度的要求。同时，耦合前后最大变形与应力值相差较大，最大变形量相差0.016063mm，最大等效应力相差187.72MPa，而最大变形位置和应力集中位置基本相同。由于耦合计算过程中流体内部流动导致流体域结构发生变化，从而对转子运动产生影响，因此比非耦合的结果更能反映出双圆弧斜齿齿轮泵转子实际的力学特性。齿轮泵转子在耦合和非耦合条件下前10阶模态频率分布对比，如图12 所示。由对比结果可知，两种情况下固有频率有一定差别，但差值较小。

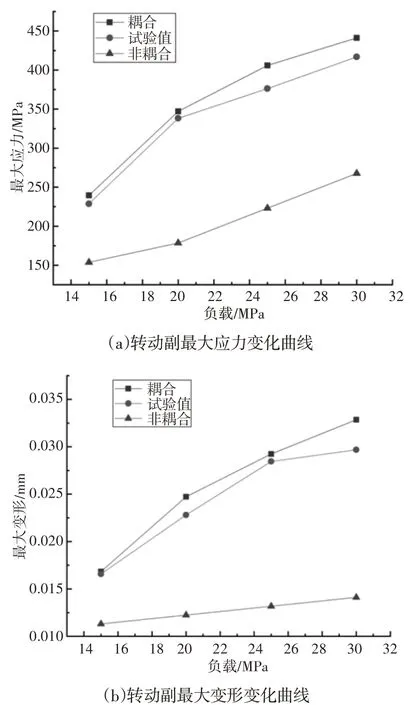
图11 转动副最大应力与变形变化曲线Fig.11 Curve of Maximum Stress and Deformation of Rotating Pair

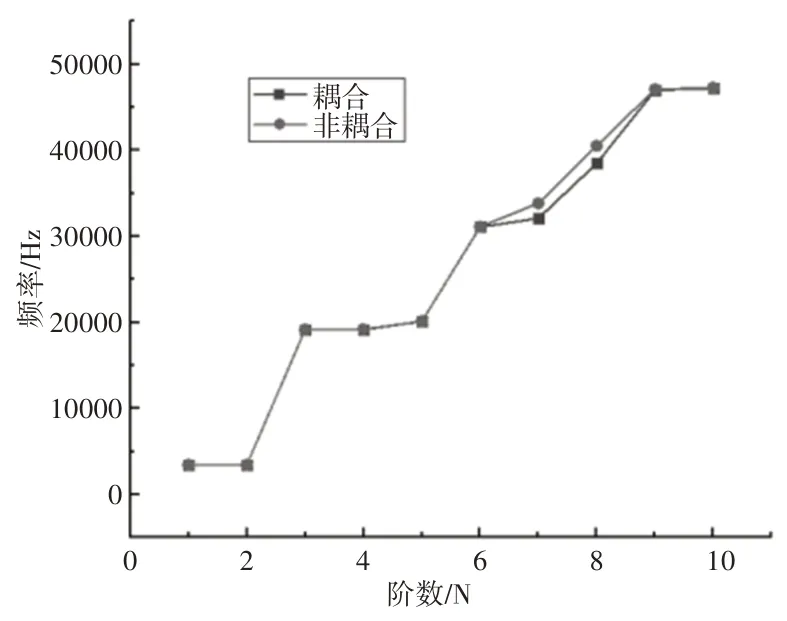
图12 耦合及非耦合模态频率分布对比Fig.12 Comparison of Frequency Distribution of Coupled and Uncoupled Modes

3 转子结构优化

高速高压齿轮泵一般用于航空航天，要求极限重量。出于减材、轻量化和提高性能的考虑，对双圆弧斜齿齿轮泵转子进行轻量化方向的结构优化，优化后的轴的大径为8mm，小径为7mm，轴的质量减少了28.32%。通过ANSYS仿真分析，设置转子出口压力为25MPa时，转动副等应力和最大位移变形量，如图13所示。

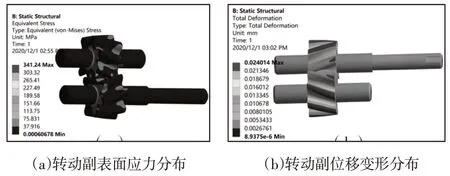
图13 转动副应力与变形分布Fig.13 Rotating Pair Stress and Deformation Distribution

由以上两种设计的计算结果对比分析可知，发现最大变形位置和应力集中位置基本一致，转子最大变形量约为0.024014mm，最大应力约为341.24MPa，最大位移变形量和最大等效应力比较于优化前有所减少。其中，最大等效应力时的安全系数表达式为：

优化后转子的安全系数得到提升，满足使用要求。

4 结论

（1）利用Fluent软件求解，使流场计算模型能够较准确预测其性能，通过对该模型的求解可以准确得到齿轮泵转动副表面的压力载荷分布，为齿轮泵内部流场研究提供依据。

（2）流固耦合影响下高速高压双圆弧斜齿轮转子的最大变形和等效应力分布，最大变形量约为0.029242mm，发生在齿轮泵转子近轮缘位置；最大等效应力发生在轴和转子相连附近，最大等效应力约405.87MPa。因此，在设计齿轮泵时应考虑此因素，需要防止此应力带来的疲劳破坏。

（3）分析流固耦合作用对转子的影响，发现负载（出油口额定压力）对转子变形与应力的影响较大。耦合前后最大变形与应力幅值相差较大，最大变形量相差0.016063mm，最大等效应力相差187.72MPa，而最大变形位置和应力集中位置基本相同。研究表明，耦合的结果更能反映出双圆弧斜齿齿轮泵转子实际转动的变化情况。

（4）对齿轮泵转子进行了质量优化，轴的质量减少28.32%，同时增大了转子的弯曲强度与接触强度，使转子拥有更长的寿命及稳定性。