考虑外部干扰的超螺旋ZNN多机械臂协调运动控制

赵 玮

（1.承德石油高等专科学校机械系，河北承德 067000；2.北京科技大学机械工程学院，北京100083）

1 引言

串行机器人，特别是串行机械臂，具有工作空间宽、速度高和灵活性高的优点，广泛应用于不同领域，例如组件装配、物体运输以及材料喷涂和切割［1−2］。但是，单个机械臂很难完成复杂的组装任务或高负荷运输任务。因此，多机械臂进行协调运动控制的研究成为了该领域研究的重点热点［3］。

作为一种特殊的递归神经网络，归零神经网络（Zeroing Neu⁃ral Network，ZNN）结合各种框架模型长期以来一直用于处理单机械臂的运动控制问题［4］。许多相关研究将焦点集中在ZNN模型在收敛性或鲁棒性方面。从收敛性能的角度出发，通过设计变参数收敛微分神经网络使得神经网络模型能够应用多准则方法，提升了收敛性能。此外，通过使用相容的凸−非凸约束双神经网络，突破了凸集的局限，并将问题求解扩展到了非凸问题［5］。从鲁棒性的角度出发，利用神经网络模型的积分信息，提出了两种新型的ZNN模型，即耐噪ZNN模型和积分增强ZNN模型，均取得了较好的效果［6］。但是在使用ZNN进行单机械臂运动控制的现有方法中，由于在没有扰动的情况下呈指数形式收敛，因此在有限时间跟踪任务中，有些具有收敛时间接近无限长，另外有些研究虽然考虑了外部干扰抑制，但仍处于渐近收敛阶段，收敛速度较慢［7］。以上两个限制严重阻碍了ZNN在复杂环境中用于多机械臂的协调运动控制的发展。

在实际复杂条件下的多机械臂的协调运动控制中，鲁棒性和收敛性对控制性能具有同等重要性，应同时考虑。由于控制理论中ST算法在非线性系统控制中的出色性能，因此利用ST算法的开发可以为构建新的ZNN统一框架提供可行的方法，从而同时实现多机械臂的协调运动控制的有限时间收敛性和鲁棒性［8］。因此提出了一种ST−ZNN多机械臂协同运动控制模型。通过两个实验对比和收敛性能测试，验证了所提出的ST−ZNN模型的有效性和优越性。

2 问题描述

对于多机械臂的一个子机器人，可以通过相关机器人关节状态来计算末端执行器的位置。对于具有m维工作空间的n自由度（n−DoF）机械臂，获取正向运动学映射：

这里，f(⋅)：Rn→Rm表示一个连续的非线性函数，其中包含特定机械臂的给定建模参数。矢量θ(t) ∈Rn表示实时关节状态矢量，而ra(t)∈Rm表示末端执行器的实时位置矢量。对于以任务执行中的实时跟踪为目标的末端执行器，一种有效的解决方案需要开发，这种方案是通过使用预定义的笛卡尔路径rp(t)∈Rm实现实时的联合状态信号θ(t)，使得：

通过计算（2）两侧的时间导数，得出：

其中J(θ(t) )∈Rm×n表示末端执行器的雅可比矩阵，计算公式为：

矢量̇(t) ∈Rn表示实时联合控制信号，其中向量(t) ∈Rm，以及向量(t)分别表示末端执行器的实时笛卡尔速度矢量和预设笛卡尔速度矢量。以上的等式（3）是以运动控制为目标的子机器人运动学的一般描述。

假设多机械臂配备有k个机械臂，根据对多机械臂的子机器人的运动学描述，得到以下正向运动学映射：

以运动控制为目标的多机械臂的速度级运动学描述为：

其中，j= 1，2，…，k。映射f j(⋅)：Rn→Rm表示第j个连续和非线性函数。向量θj(t) ∈Rn表示第j个机械臂的实时联合状态向量。矩阵Jj(θ(t)) ∈Rm×n表示第j个机械臂末端执行器的雅可比矩阵。向量(t) ∈Rm和向量(t)分别表示末端执行器的实时笛卡尔速度矢量和预定义笛卡尔速度矢量。在实际应用中，例如物体运输，为多机械臂的协调运动控制不可避免地需要考虑外部干扰。因此，考虑外部干扰多机械臂的运动控制模型为：

其中，ρj∈Rm是在第j个机械臂末端执行器中注入的矢量形式的外部干扰，用于跟踪预定路径。

大量研究表明，ZNN常规框架逼近平衡点的解的指数收敛性和无限时动态响应已得到了验证［9］。相关的传统ZNN模型可在外部干扰的影响下用于多机械臂的协调运动控制，其公式如下：

其中，(Jj(θ(t)))†∈Rn×m表示第j个机械臂的雅可比矩阵Jj(θ(t))的伪逆。向量uj(t)表示发送到第j个机械臂的控制输入信号，参数γ∈R+是预定义的参数。因此，可以得到多机械臂的整个控制输入矩阵为：U(t) =[u1(t)u2(t)…uj(t)…uk(t)]T∈Rk×n。

引理1［10］：假设多机械臂都不受外部干扰，如果应用正设计参数γ> 0 ∈R，第j个机械臂从任意初始位置(0) ≠(0)开始，则末端执行器轨迹(t)通过传统ZNN模型（8）对于具有k个子机器人的多机械臂的协调运动控制问题（6），时间t趋于+∞时，全局收敛到预定路径(t)，指数收敛率为γ。

引理2［11］：假设第j个机械臂受到外部干扰ρj的影响，如果使用预定义参数γ> 0 ∈R，并且第j个机械臂从任意初始位置(0) ≠(0)开始，则向量值误差函数εj(t) =(t) −(t)在时间t∈[0，+∞)经由传统ZNN模型（8）收敛到具有最高点的稳态误差，即对于具有k个子机器人的多机械臂的协调运动控制问题，

以上引理说明，在假设模型不受外部干扰的情况下，由于指数收敛特性，传统ZNN 模型（8）的解有趋于无限大的收敛时间。此外，在稳态下所产生的残余误差仍然是存在外部干扰的前提。

3 ST−ZNN

3.1 ST-ZNN设计框架

对于多机械臂的协调运动控制，可以从第j(j= 1，2，…，k)个子机器人开始设计框架，其中k是多机械臂的数量。在多机械臂开始运动控制任务之前，需要输入第j个机械臂的末端执行器，该预定义路径具有由(t)表示的3D 曲线方程。然后，第j个机械臂的矢量形式误差函数εj(t) ∈Rm是用来在瞬态和稳态下测量末端执行器的预定义路径(t)与实际轨迹(t)之差，用第i个元素定义为：

其中，i= 1，2，…，m。为了使误差函数(t)的每个元素在有限时间内具有扰动抑制特性收敛至零，可以设计调零神经动力学设计公式并将其用于：

其中，参数φ> 0 ∈R是用户预定义的参数(t)表示中间矢量形式的变量，可充分利用时间积分信息作为来自多机械臂的反馈来抑制外部干扰ρj，进一步描述：

因此，一个完整的动力学方程可以集成到以下方程中：

式（12）中描述的方程正好是ST算法的动力学方程，其一般描述为：

其中，s1=(t)，s2=(t)。参数l1= 2φ和l2=φ2是ST算法的两个设计参数。另外，参数p= 1/2通常是根据控制理论中的ST算法设置的。文献［11］已经研究了ST算法在控制理论中的严格理论发展。ST算法的应用包括系统控制、干扰观测和鲁棒的精确区分。可以通过利用ST算法来有效设计鲁棒的控制器，而无需先验估计。

通过利用上述（12）中描述的ST算法，矢量值神经动力学方程的第i个元素描述如下：

等式（14）可以写成第j个机械臂的以下向量形式：

其中向量映射功能数组Sigp(⋅)：Rm→Rm的第i个元素被定义为：

同时，i= 1，2，…，m。

回忆方程式（7）中描述的具有外部干扰的多机械臂的运动控制目标，动力学式（17）用速度级的控制输入信号uj(t)表示为以下形式：

因此，可以得到多机械臂的整个控制输入矩阵，即U(t) =[u1(t)u2(t)…uj(t)…uk(t)]T∈Rk×n。

人作为多个机器人用户，通过在用于整个机器人控制系统的主计算机中给出指令。然后，指令作为输入信息rp(t)和ṙp(t)传输到机器人计划器和求解器。最后，由求解器生成的解被传输到控制系统的执行器，即多机械臂，用于执行诸如携带物体之类的主要任务。整个控制系统是一个不使用遥控的自主机器人系统。

3.2 理论分析

定理1：ST−ZNN模型的全局稳定性和收敛性。假设多个机械臂都不受外部干扰。如果使用正的预定义参数φ> 0 且p= 1/2，则第j个机械臂从第i个任意初始位置(0) ≠(0)和任意初始误差(0) ≠0开始，则ST−ZNN模型（18）全局稳定，对于具有i= 1，2，…，m和j= 1，2，…，k的k个子机器人的多机械臂的协调运动控制问题（7），在Lyapunov的意义上，末端执行器轨迹的第i个元素(t)全局收敛于第i个预定义路径(t)。

证明：对于多机械臂，第j个子机器人的第i个子系统的ST−ZNN模型（18）的动力学方程式等效于在多机械臂都不受外部干扰条件下处理协调运动控制问题（7）的下列方程：

参数为p= 1/2。请注意，必须继续使用Lyapunov候选函数。定义以下Lyapunov函数候选：

当且仅当(t) = 0 时，上面的Lyapunov 函数候选κ(t) =φ2(t) |+((t))2/2是不连续的。(t) = 0恰好是所提出的用于多机械臂协调运动控制的ST−ZNN模型（18）的解决方案。在第j个机械臂从第i个任意初始位置(0) ≠(0)和任意初始误差(0) ≠0 开始的情况下，Lyapunov 函数候选κ(t)保持连续。因此，鉴于(t) ≠0时κ(t) > 0，并且仅(t) = 0时κ(t) = 0，κ(t)是正定的。随后，可以计算出κ(t)的时间导数为：

因此，对于设计参数φ> 0和p= 1/2，对于时间t∈[0，+∞)，(t)是负定的。基于Lyapunov稳定性理论以及对不连续系统La⁃Salle 不变性原理的推广，ST−ZNN 模型（18）在误差函数(t) =(t) −(t)的第i个子系统中是全局稳定的，全局收敛到0。由此得出，对于多机械臂的第j个子机器人，第i个末端执行器轨迹(t)全局收敛于第i个预定义路径(t)。

第j个机械臂从第i个任意初始位置(0) ≠(0)，即任意初始误差(0) ≠0开始。其中(t) = 0正是所提出的用于多机械臂协调运动控制的ST−ZNN模型（18）的解决方案。ST−ZNN模型（18）的全局稳定性和收敛在原点附近但不包含原点（或称为平衡点(0) ≠0）时成立。证明完成。

定理2：ST−ZNN模型的有限时间收敛。假设多个机械臂都不受外部干扰。如果使用预定义参数φ> 0且p= 1/2，并且第j个机械臂从任意初始状态开始，且在时间实例t= 0 时误差(0) ≠0，则第i个实际轨迹(t)通过提出的ST−ZNN模型（18）在以下有限时间Tf中全局收敛到第i个预定义路径(t)：

证明：对于第j个子机器人机械臂的第i个子系统，选择一个中间变量为：

然后，通过代入中间变量J(t)，状态等式（12）可以改写为：

以及：

同时，p= 1/2。因此，可以很容易地具有以下动力学方程：

将Lyapunov函数候选定义为：

随后，它遵循Η(t)的时间导数为：

根据式（27），可以得到：

通过将式（31）代入式（30），可以进一步获得：

注意：

永远成立。等价于：

所以存在：

进一步得到：

通过结合式（32）、式（36）的结果，可以得到：

因此，可以将（37）重新表示为：

等式（38）等于：

通过在式（39）的两侧进行积分，可以得出：

以及等式（40）会导致：

因此得出：

从式（42）可以很容易地发现，对于p= 1/2和：

使得Η(t) = 0。

根据结果式（43）、式（37），得出结论，当t≥时，Η(t) = 0成立。因此，结果是，第j个机械臂从第i个任意初始位置(0) ≠(0)开始，且初始误差(0) ≠0，由ST−ZNN 模型（17）合成的第i个实际轨迹(t)在有限时间全局收敛到第i个预定义路径(t)。此外，由于：

等式χji(0) = 0成立，得出：

其中，中间变量J(t)仅对于(t) = 0是不可微的。当(t) =0时正是所提出的用于多机械臂协调运动控制的ST−ZNN 模型（18）的解决方案。仅在原点（或称为平衡点）处，对于(t) = 0，状态系统（25）和（26）也是不可微的。因此，不等式（44）在原点附近但不包含原点的情况下成立，即，第j个机械臂从第i个任意初始位置(0) ≠(0)开始，并且存在任意初始误差(0) ≠0。证明完成。

定理3：带有外部干扰的ST−ZNN模型的全局稳定性和收敛性。假设第j个机械臂受到外部干扰ρj的影响。如果使用预定义参数φ> 0 且p= 1/2，则第j个机械臂从第i个任意初始位置(0) ≠(0)和任意初始误差(0) ≠0 开始，则ST−ZNN 模型（18）全局稳定，对于具有i= 1，2，…，m和j= 1，2，…，k的k个子机器人的多机械臂的协调运动控制问题（7），在Lyapunov的意义上，末端执行器轨迹的第i个元素(t)全局收敛于第i个预定义路径(t)。

证明：给定第j个子机器人机械臂的ST−ZNN 模型（18）存在附加扰动ρj，则第i个动态子系统对应于ST−ZNN模型（18）的误差函数εj(t)可以描述为：

选择一个中间变量：

得到：

其中，i= 1，2，…，m且̇ = 0。与定理1 中的步骤相似，将Lyapunov函数候选定义为：

因此，鉴于对于(t) ≠0的l(t) > 0，l(t)是正定的，并且仅对于(t) = 0时，l(t) = 0。那么，l(t)的时间导数为：

因此，对于设计参数φ> 0 和p= 1/2，当时间t∈[0，+∞)，l̇(t)是负定的。基于Lyapunov 稳定性理论以及不连续系统La⁃Salle不变性原理的一般化，对于第j个机械臂，在第i个子系统下的误差函数(t) =(t) −(t)全局收敛于0时，具有加性常数扰动的ST−ZNN 模型（18）是全局稳定的。换句话说，第j个机械臂的第i个末端执行器轨迹(t)全局收敛到第i个预定义路径(t)。类似地，第j个机械臂从第i个任意初始位置(0) ≠(0)开始，即，任意初始误差(0) ≠0。请注意，情形(t) = 0正是提出的用于多机械臂协调运动控制的具有加性常数扰动的ST−ZNN模型（18）的解决方案。具有加性常数扰动的ST−ZNN模型（18）的全局稳定性和收敛性在原点附近但不包含原点（或称为平衡点(0) ≠0）时成立。证明完成。

定理4：具有外部干扰的ST−ZNN模型的有限时间收敛。假设第j个机械臂受到外部干扰ρj的影响。如果使用预定义参数φ> 0 且p= 1/2，则第j个机械臂从第i个任意初始位置(0) ≠(0) 和任意初始误差(0) ≠0 开始，则具有i=1，2，…，m和j= 1，2，…，k的k个子机器人的多机械臂协调运动控制问题（7）的ST−ZNN 模型（18）是全局稳定的，末端执行器轨迹的第i个元素(t)在有限时间Tf中收敛于第i个预定义路径(t)。

此外，有限的收敛时间与多机械臂的外部干扰ρ的值无关。

证明：鉴于加性常数扰动ρ≠0时的ST−ZNN 模型（18）与无扰动情况下的动力学方程相同，如（12）所示。因此，通过与（24）和（25）相同的J(t)变量替换，可以从定理1中的步骤推广出相同的结果。证明完成。收敛时间Tf取决于预定义参数φ和初始误差(0)。当初始误差(0)大时，φ应该更大，以使收敛时间Tf缩短。请注意，参数φ是提出的ST−ZNN模型（18）的重要参数，该模型由从业者预先定义。理论上，可以设定满足φ> 0 ∈R的任意值。有限收敛时间Tf与预定义参数φ成反比。为了缩短收敛时间，可以将预定义参数φ的值设置为硬件在实际机器人应用中允许的适当大小［12］。

4 实验结果与分析

ST−ZNN 模型的设计过程说明了一种用于多机械臂协调运动控制的新框架，其中许多实际应用都适合于ST−ZNN框架。在本节中，对多机械臂系统进行了两个验证性任务，并对结果进行了比较和测试，其中，每个机器人都是k= 3和k= 4的PUMA560冗余机械臂。不失一般性，将机器人系统的持续时间设置为Td=5s。第j个PUMA560 机器人的关节角矢量的初始值设置为θj(0) =[0，−π/4，0，2π/3，−π/4，0]Trad，关节速度矢量的初始值设为(0) =[0，0，0，0，0，0]Trad/s。两个说明性任务和比较中的预定义参数设置为φ= 2，注入到第j个机器人中的外部干扰设置为ρj=[0.06，0.04，0.05]。

4.1 任务1：三角形物体运输

图1显示了用于多机械臂来运输具有外部干扰的三角形物体的ST−ZNN模型（18）的结果。图1（a）说明了3D视图中用于多机械臂运输三角形物体的运动控制过程。多个机械臂协调配合。有效的协调运动控制可以在图1（b）的另一个视图中找到。末端执行器的三个实际轨迹在过渡状态下快速且和谐地朝着预定路径移动，并最终在稳态下与预定运动路径重叠，如图1（c）所示。残留误差验证了每个PUMA560 机器人的有限时间收敛性，如图2（d）所示。数值研究中的收敛时间tc约为0.2s，与t≥的结果一致。

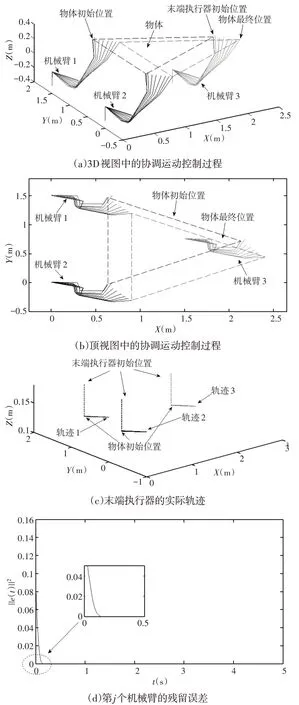
图1 提出的ST−ZNN模型（17）进行协调运动控制结果Fig.1 Proposed ST−ZNN Model（17）for Coordinated Motion Control Results

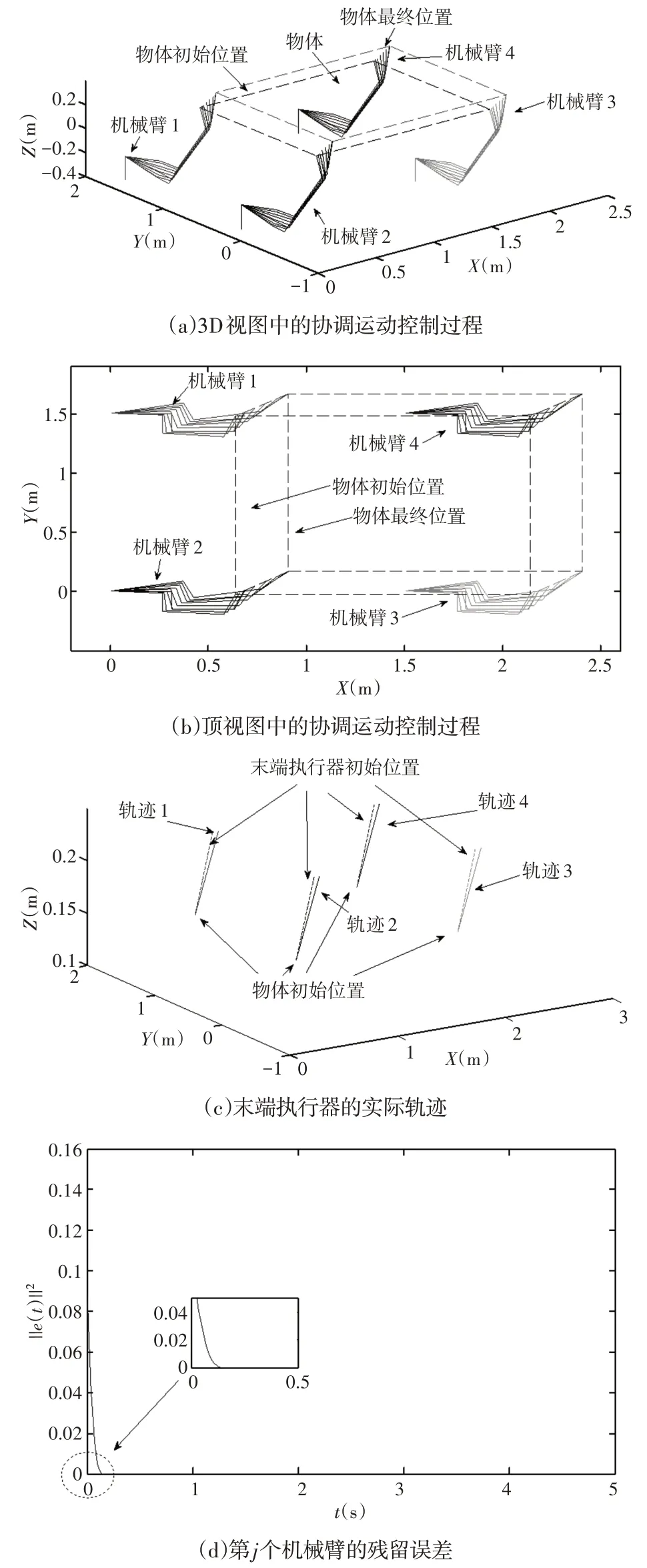
图2 当ST−ZNN模型（17）进行协调运动控制结果Fig.2 Results of Coordinated Motion Control when St−Znn Model（17）is Applied

4.2 任务2：矩形物体运输

图2 显示了用于多机械臂来运输具有外部干扰的矩形物体的ST−ZNN模型（18）的结果。图2（a）展示了3D视图中用于多机械臂运输这个大物体的运动控制过程。运动过程的另一个视图可以在图2（b）中找到。四个末端执行器的实际轨迹在过渡状态下快速且有效地朝着预定义的运动路径移动，并最终在稳态下与预定义的路径重叠，如图2（c）所示。残留误差也说明了有限时间收敛性，如图2（d）所示。数值研究中的收敛时间tc也约为0.2s，与结果一致。

4.3 比较

传统ZNN模型（8）和ST−ZNN模型（18）进行了比较，以进行无外部干扰和有外部干扰的协调运动控制。如图3、图4 所示。多机械臂的末端执行器通过无外部干扰的模型（8）和模型（18）传输三角形和矩形物体，从而说明了不同的收敛性能，如图3（a）、图3（c）所示。通过提出的ST−ZNN模型进行的运输运动在两个任务中均显示出在瞬态下更快的运动速度。残留误差验证了ST−ZNN 模型（18）有具有较短收敛时间tc的有限时间收敛特性，如图3（b）、图3（d）所示。在外部干扰注入的情况下，通过ST−ZNN 模型（18）产生的残留误差仍然具有鲁棒性和有限时间收敛性，而通过传统ZNN 模型（8）产生的残留误差具有更高的稳态误差。综上所述，所提出的ST−ZNN 模型（18）同时具有有限时间收敛性和对外部干扰的鲁棒性，与现有研究相比取得了新的进展。

图3 比较了传统ZNN模型（7）和ST−ZNN模型（17）的协调运动控制效果Fig.3 Compares the Coordinated Motion Control Effects of Traditional ZNN Model（7）and ST−ZNN Model（17）

图4 比较了传统ZNN模型（7）和ST−ZNN模型（17）在有外部干扰条件下，多机械臂的末端执行器运输三角形和矩形物体时的协调运动控制效果Fig.4 Compares the Coordinated Motion Control Effect of Traditional ZNN Model（7）and ST−ZNN Model（17）in the Transportation of Triangle and Rectangular Objects by the end Effector of Multiple Mmanipulators under the Condition of External Interference

4.4 测试

首先，如果在相同的初始机器人系统状态和相同的外部干扰下，参数φ的值从1增加到5，如图5所示。残留误差表现出较短的收敛时间。已经证明，ST−ZNN模型（18）的有限收敛时间理论上为预定义参数φ的值越大，所得解的有限收敛时间越短。其次，如果第j个机器人的初始误差εj(0)的值与相同的设计参数φ和相同的外部干扰一起减小，则产生的残留误差说明收敛时间更短，如图6所示。结果与理论分析一致。

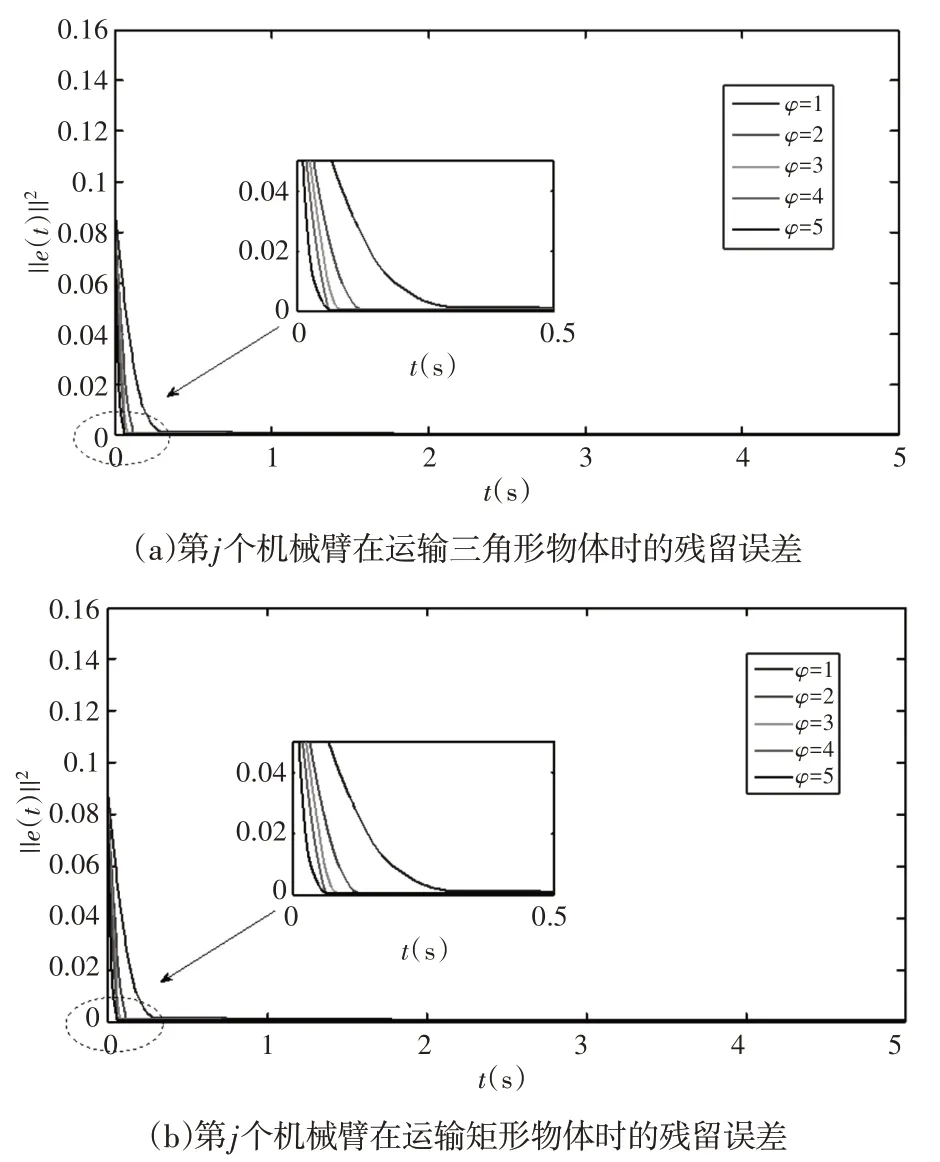
图5 在预定义参数的不同值条件下，多机械臂的末端执行器运输三角形和矩形物体时，通过ST−ZNN模型（17）进行的协调运动控制过程中的残留误差Fig.5 The Residual Error of the ST−ZNN Model（17）in the Coordinated Motion Control Process of the Multi Manipulator’s end Effector Transporting Triangular and Rectangular Objects Under Different Values of the Predefined Parameters

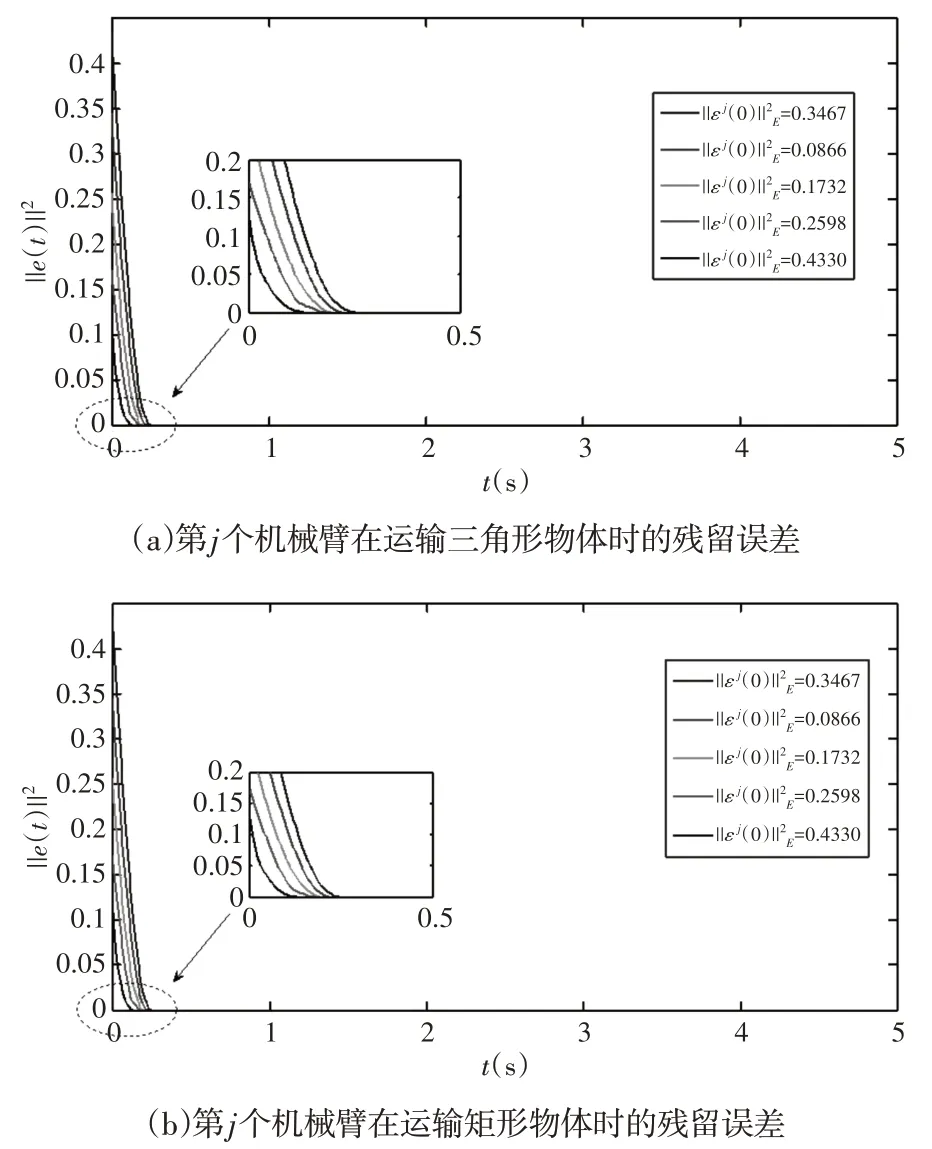
图6 在不同初始位置条件下，多机械臂的末端执行器运输三角形和矩形物体时，通过ST−ZNN模型（17）进行的协调运动控制过程中的残留误差Fig.6 The Residual Errors in the Process of Coordinated Motion Control by ST−ZNN Model（17）When the end Effector of Multi Manipulator Transports Triangular and Rectangular Objects Under Different Initial Positions

最后，利用图7所示的第j个机器人的剩余误差，研究了不同外部干扰对ST−ZNN模型（18）的影响。由此产生的残留误差在两个跟踪控制任务中表现出几乎相同的收敛性，也就是说，在相同的设计参数φ和初始执行器状态下，在不同的外部干扰ηi(i=1，2，…，5)下，收敛时间相同，如图7所示。有限的收敛时间与外部干扰无关。

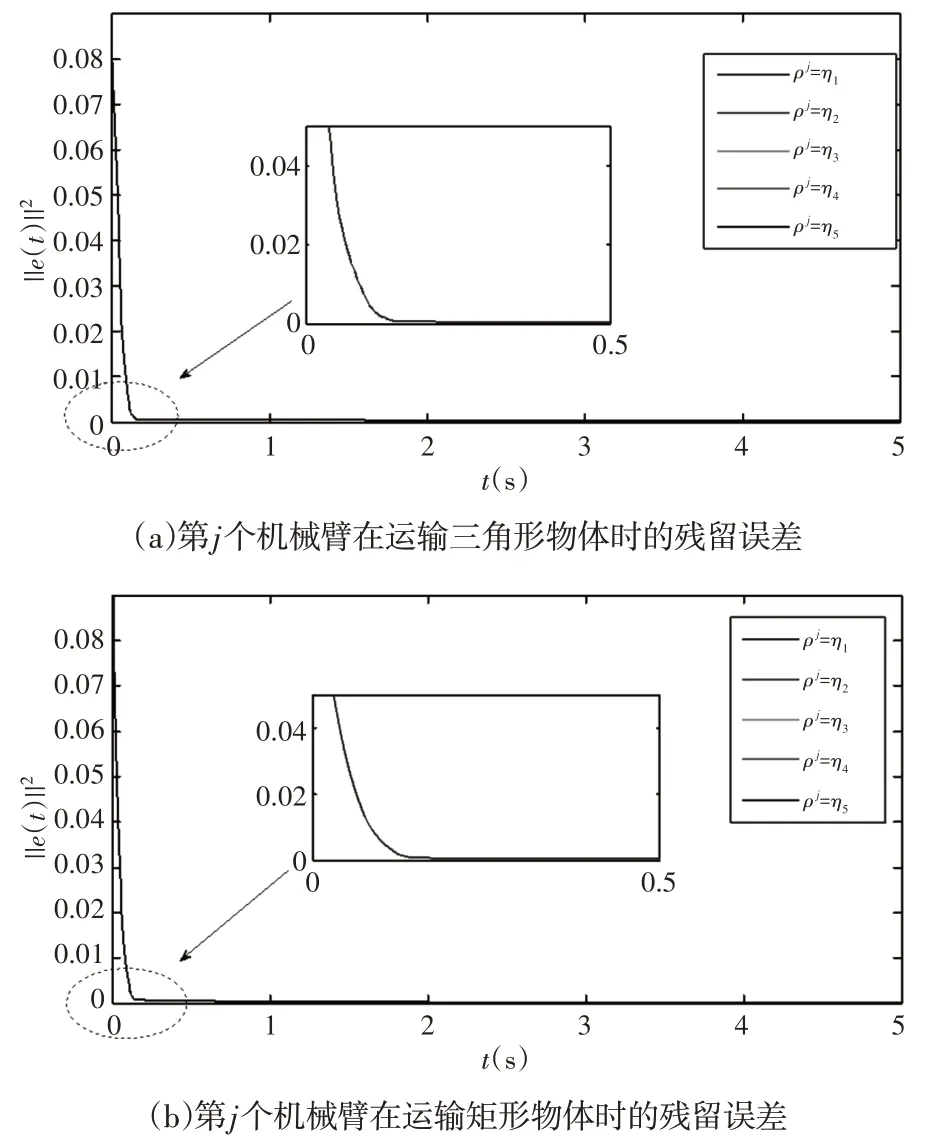
图7 不同外部干扰值的条件下，多机械臂的末端执行器运输三角形和矩形物体时，通过ST−ZNN模型（17）进行的协调运动控制过程中的残留误差Fig.7 The Residual Error of the ST−ZNN Model（17）in the Coordinated Motion Control of the End Effector of the Multi Manipulator in the Transportation of Triangular and Rectangular Objects Under Different External Interference Values

5 结论

为了解决传统ZNN存在的缺点，提出了一种ST−ZNN多机械臂协调运动控制模型。通过理论分析证明与两个多机械臂协调运动控制实例验证得出如下结论：

（1）ST−ZNN模型与传统ZNN相比，在不同的外部干扰条件下，具有更快的瞬态运动速度、更短的收敛时间以及更小的残留误差，验证了提出方法相对于传统ZNN的优越性。（2）ST−ZNN模型中，预定义参数的值越大，所得解的有限收敛时间越短，有限收敛时间的大小以及残留误差的收敛性均与外部干扰大小无关。（3）所提出的ST−ZNN模型在具有干扰的多机械臂协调运动控制具有全局稳定性、有限时间收敛性和鲁棒性，能够有效地实现外部干扰条件下的多机械臂协调运动控制。