基于BP神经网络的陕北黄土高原沟壑密度空间插值研究

孙京禄　张贝尔　王淑文　陆贝贝

［关键词］BP神经网络；沟壑密度；空间插值；辅助变量；陕北黄土高原

［摘要］沟壑密度是反映地表破碎度的重要因子，也是进行水土保持综合调查、制定流域综合治理规划的重要指标依据。因缺乏高精度的大尺度DEM数据，故选择合适的插值方法实现沟壑密度在区域尺度上的空间插值是迫切需要解决的科学问题。BP神经网络插值在区域尺度地理要素空间变异研究中，特别是小样本情况下，具有更高的精度。基于陕北黄土高原80个试验样区5 m分辨率DEM和将30 m分辨率DEM计算得到的研究区平均坡度作为辅助变量，利用BP神经网络插值方法进行陕北黄土高原沟壑密度插值，并与不同插值方法结果进行精度对比，结果表明：当处理目标变量与辅助变量之间存在相关关系却不存在一个准确关系式时，BP神经网络插值具有优越性，插值结果精度更高。此外，还对比了基于不同辅助变量的BP神经网络插值精度，结果表明：对于样本点稀疏、地形起伏较大的区域尺度空间插值，采用辅助变量的BP神经网络插值精度明显高于不采用辅助变量，且选取的辅助变量必须与目标变量有较强的相关性，增加相关系數低的辅助变量反而会导致插值精度降低。

［中图分类号］ P208；S157［文献标识码］ A［文章编号］ 1000－0941（2023）08－0024－04

沟壑密度是衡量黄土高原地区地貌发育阶段、影响侵蚀产沙过程的重要地形参数，也是进行水土保持综合调查、制定流域综合治理规划的重要指标依据[1-2]，因此准确计算黄土高原地区沟壑密度具有重要现实意义。目前，沟壑密度的计算主要是基于数字高程模型（DEM）提取沟谷网络，然后统计研究区沟谷网络总长度，研究区沟谷网络总长度与研究区面积的比值即为沟壑密度[3]。然而，DEM分辨率对沟壑密度计算结果的准确性有很大的影响，只有采用高分辨率DEM数据才可以得到比较准确的沟壑密度结果[4-5]。由于缺乏符合要求的大尺度数据，目前难以实现基于高分辨率DEM的黄土高原地区沟壑密度计算，因此在计算样区沟壑密度的基础上，选择合适的插值方法实现沟壑密度在区域尺度上的空间插值是迫切需要解决的科学问题。

目前广泛应用的插值方法主要包括反距离加权插值、样条函数插值、克里金插值等方法，这些方法有各自的优缺点和适用条件，在样本数目有限、插值区域较大时，插值结果的精度难以保证[6]。以克里金插值法为基础，利用辅助变量衍生出的插值方法包括局部平均的简单克里金法、具有外部漂移的克里金法、协同克里金法、回归克里金法等[7-8]，这些方法可以有效地提高估值精度，被广泛应用于中小尺度地理要素的空间估值中。但是，除协同克里金法外，这些插值方法的应用前提是待估值变量与辅助变量之间存在一个明确的关系。

然而，大多数情况下二者之间存在较强的相关关系，却不存在一个准确的关系式[9-10]。人工神经网络作为一种用计算机模拟生物机制的方法，无须事先确定输入、输出量之间映射关系的数学方程，仅通过自身的训练，学习某种规则，在给定输入值时可得到最接近期望输出值的结果，其分析原理使得这种方法对解决机理尚不明确的问题十分有效[11]。其中BP（Back Propagation）神经网络属于多层前馈神经网络，具有高度的非线性映射能力[12-13]，许多研究表明在大尺度地理要素空间变异研究中，特别是在小样本情况下，BP神经网络插值方法具有更高的精度[14]。因此，本研究以陕北黄土高原为例，采用BP神经网络方法进行沟壑密度插值，并与其他插值方法进行对比，分析BP神经网络插值结果精度，以期为获取区域尺度沟壑密度结果提供借鉴和参考。

1研究区概况

陕北黄土高原是黄土高原的核心地区之一，主要包括陕西省榆林市和延安市。该区以黄土地貌为主，黄土塬、梁、峁及沟壑等地貌发育十分典型，基本涵盖了黄土高原大部分的地貌组合及景观形态。其中，北部主要为沙丘、草滩等风沙地貌；中部主要为黄土梁、峁、丘陵、沟壑等地貌，并分布有石质山岭；西部为低山丘陵地貌；南部主要为黄土残塬、黄土台塬等地貌。属温带半干旱和暖温带半干旱气候区，降水主要集中在夏季和秋季，易形成暴雨径流侵蚀地面，造成严重水土流失。

2研究方法

2.1数据处理

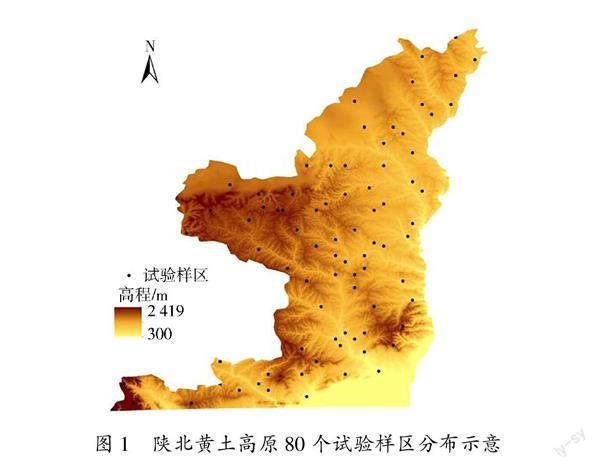
在研究区选择涵盖不同地貌类型、均匀分布的80个试验样区（见图1），采用每个样区5 m分辨率DEM计算沟壑密度，作为BP神经网络插值的基础数据，5 m分辨率DEM数据来源于陕西省测绘局；此外采用覆盖研究区的30 m分辨率DEM计算研究区平均坡度，作为BP神经网络插值的辅助变量，30 m分辨率DEM数据来源于地理空间数据云网站（https：//www.gscloud.cn/）。

2.2BP神经网络插值

2.2.1插值过程

BP神经网络包括输入层、隐藏层、输出层3层，理论上3层BP网络可以逼近任何有理函数[15]。BP神经网络算法包括信号的正向传播和误差的反向传播两个过程，其中在正向传播过程中，BP神经网络通过隐藏层神经元对数据进行处理，并输出相应结果；在反向传播过程中，BP神经网络通过对比真实结果与预测结果之间的误差来不断调整各层神经元的参数值，从而减小误差，达到理想效果。本研究将80个试验样区分为72个训练样本和8个检验样本，通过Matlab软件中神经网络工具箱完成BP神经网络插值计算，主要过程包括：数据导入→随机产生训练集和测试集→创建BP神经网络→设置训练参数→训练网络→仿真测试→数据反归一化→性能评价。

2.2.2插值方法对比

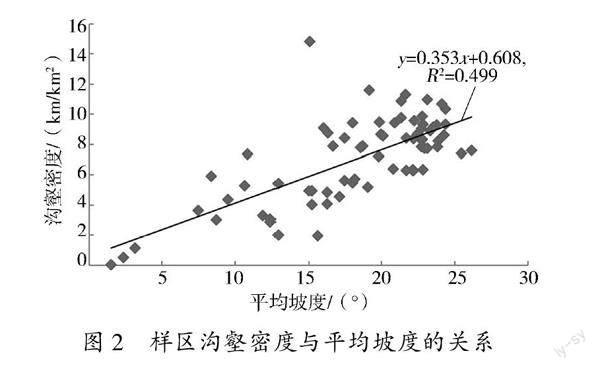
为了对比分析BP神经网络插值的精度，通过ArcGIS软件分别采用样条函数、反距离加权、协同克里金、回归克里金等方法进行插值，其中协同克里金法的协同变量为研究区平均坡度，回归克里金法的回归模型采用试验样区沟壑密度和平均坡度的线性拟合公式（见图2）。此外，为了对比分析基于不同辅助变量的BP神经网络插值精度，设置了研究模型和3个对比模型：①研究模型指辅助变量为研究区平均坡度；②对比模型Ⅰ指不采用辅助变量；③对比模型Ⅱ指辅助变量为3个邻近点坐标值；④对比模型Ⅲ指辅助变量为3个邻近点坐标值和研究区平均坡度。

插值结果的精度分析采用平均绝对误差和均方根误差2个误差评价指标，其中平均绝对误差反映了估值的误差范围，均方根誤差反映了估值的灵敏度和极值情况，平均绝对误差和均方根误差越小代表插值结果精度越高，计算公式分别为

式中：VMAE和VRMSE分别为平均绝对误差值和均方根误差值；n为检验样本数量，本研究中n=8；Pi和Ai分别为检验样本中的沟壑密度的插值结果和实际计算值。

3结果与分析

表1是不同插值方法的误差评价结果，插值结果精度从高到低依次是：BP神经网络插值法、回归克里金法、协同克里金法、反距离加权插值法、样条函数插值法。有研究表明，对于小区域的地理要素估值，如目标变量与辅助变量的相关系数在0.5以上，则采用协同克里金法插值时可以提高估值精度；如目标变量与辅助变量的相关系数在0.7以上，则采用基于目标变量与辅助变量的回归模型的回归克里金法插值时可以提高估值精度[16-17]。由表1可知，

回归克里金法和协同克里金法的插值精度高于反距离加权插值法和样条函数插值法，表明对于大区域的地理要素估值，回归克里金法和协同克里金法在一定程度上可以提高插值精度。以区域平均坡度作为辅助变量的BP神经网络插值精度高于回归克里金法和协同克里金法，这是由于尽管平均坡度和沟壑密度之间存在相关关系，但是由图2可知，样区平均坡度和沟壑密度的线性拟合决定系数为0.499，数据点的分布相较于拟合直线较为分散，二者之间的回归关系不够显著。因此，当处理目标变量与辅助变量之间存在相关关系，却不存在一个准确关系式时，BP神经网络插值具有优越性。

此外，本研究还对比了基于不同辅助变量的BP神经网络插值精度，结果表明插值精度从高到低依次是：研究模型、对比模型Ⅲ、对比模型Ⅱ、对比模型Ⅰ（见表2）。不采用辅助变量的BP神经网络插值精度最低，在采用3个邻近点坐标值作为辅助变量后，插值精度有一定程度的提升；在采用3个邻近点坐标值和研究区平均坡度作为辅助变量后，插值精度进一步提升。然而，BP神经网络插值精度最高的是采用研究区平均坡度作为辅助变量，表明增加辅助变量并不能使插值精度保持增加。通过计算，得到试验样本沟壑密度与平均坡度、第一邻近点沟壑密度、第二邻近点沟壑密度、第三邻近点沟壑密度的相关系数分别为0.707、0.552、0.540、0.415（显著性水平均为0.01）。可以看出，对于样本点稀疏、地形起伏较大的区域尺度空间插值，采用辅助变量的BP神经网络插值精度明显高于不采用辅助变量，然而选取的辅助变量必须与目标变量有较强的相关性，由于试验样区沟壑密度与邻近点沟壑密度的相关系数并不高，因此当已选择研究区平均坡度作为辅助变量时，再增加3个邻近点坐标值作为辅助变量（对比模型Ⅲ），其插值精度相比于研究模型反而下降，表明提升BP神经网络插值精度需要增加相关系数高的辅助变量，若增加相关系数低的辅助变量往往会造成多重共线性，导致插值精度降低[18]。

基于BP神经网络的陕北黄土高原沟壑密度插值结果见图3，陕北黄土高原沟壑密度在空间分布上总体呈现中部和东北部高、西北部和南部低的特点。北部地区地势相对平坦，沟壑密度较小；中部地区沟壑纵横，沟壑密度相对较大，这也是陕北黄土高原水土流失最严重的地区；南部地区主要是较平坦的塬面，侵蚀发育处于幼年期，沟壑密度相对较小。

4结论

沟壑密度是反映地表破碎度的重要因子，在土壤侵蚀、地貌演变等研究中具有重要作用，因此对于黄土高原等土壤侵蚀严重地区，精准估算区域尺度沟壑密度具有重要意义。BP神经网络插值在大尺度地理要素空间变异研究中，特别是在小样本情况下，具有更高的精度。本研究基于陕北黄土高原80个试验样区5 m分辨率DEM和将30 m分辨率DEM计算得到的研究区平均坡度作为辅助变量，利用BP神经网络插值方法进行陕北黄土高原沟壑密度插值，并与样条函数插值法、反距离加权插值法、协同克里金法、回归克里金法的沟壑密度插值结果进行对比，结果表明：插值结果精度从高到低依次是：BP神经网络插值法、回归克里金法、协同克里金法、反距离加权插值法、样条函数插值法。当处理目标变量与辅助变量之间存在相关关系，却不存在一个准确关系式时，BP神经网络插值具有优越性。此外，本研究还对比了基于不同辅助变量的BP神经网络插值精度，结果表明对于样本点稀疏、地形起伏较大的区域尺度空间插值，采用辅助变量的BP神经网络插值精度明显高于不采用辅助变量，然而选取的辅助变量必须与目标变量有较强的相关性，若增加相关系数低的辅助变量反而会导致插值精度降低。

[参考文献]

[1] 赵文武，傅伯杰，陈利顶.陕北黄土丘陵沟壑区地形因子与水土流失的相关性分析[J].水土保持学报，2003，17（3）：66-69.

[2] 卢金发.黄河中游流域地貌形态对流域产沙量的影响[J].地理研究，2002，21（2）：171-178.

[3] 田剑，汤国安，周毅，等.黄土高原沟谷密度空间分异特征研究[J].地理科学，2013，33（5）：622-628.

[4] 李俊，汤国安，张婷，等.利用DEM提取陕北黄土高原沟谷网络的汇流阈值研究[J].水土保持通报，2007，27（2）：75-78.

[5] 沈晶玉，史明昌，田玉柱，等.DEM网格尺寸与沟谷提取精度研究[J].中国水土保持，2007（2）：56-60.

[6] 朱会义，刘述林，贾绍凤.自然地理要素空间插值的几个问题[J].地理研究，2004，23（4）：425-432.

[7] 刘志华，常禹，贺红士，等.基于辅助变量的森林半腐层厚度空间插值精度[J].应用生态学报，2009，20（1）：77-83.

[8] 鲁程鹏，束龙仓，张颖，等.稀疏数据插值问题的回归克里格方法[J].水电能源科学，2009，27（1）：81-84.

[9] 姜勇，梁文举，李琪.利用与回归模型相结合的克里格方法对农田土壤有机碳的估值及制图[J].水土保持学报，2005，19（5）：97-100，126.

[10] 邓羽，刘盛和，姚峰峰，等.基于协同克里格的基准地价评估及空间结构分析[J].地理科学进展，2009，28（3）：403-408.

[11] 尤淑撑，严泰来.基于人工神经网络面插值的方法研究[J].测绘学报，2000，29（1）：30-34.

[12] 鹿应荣，杨印生，刘洪霞.基于BP神经网络的非线性组合预测模型在粮食物流需求预测中的应用[J].吉林大学学报（工学版），2008，38（增刊2）：61-64.

[13] 林宇锋，邓洪敏，史兴宇.基于新的改进粒子群算法的BP神经网络在拟合非线性函数中的应用[J].计算机科学，2017，44（增刊2）：51-54.

[14] 王汉涛，张潇潇.仿生算法优化BP神经网络在降雨空间插值中的应用[J].水资源与水工程学报，2019，30（3）：106-112.

[15] 赵明伟，汤国安，李发源，等.基于BP神经网络的陕北黄土高原侵蚀产沙影响因子显著性研究[J].水土保持通报，2012，32（1）：5-9，226.

[16] 刘艳芳，宋玉玲，郭龙，等.结合高光谱信息的土壤有机碳密度地统计模型[J].农业工程学报，2017，33（2）：183-191.

[17] 张欢，高小红.复杂地形区土壤有机质空间变异性分析及制图[J].水土保持研究，2020，27（5）：93-100.

[18] 秦雯怡，陈果，李小臻，等.基于机器语言的岷江上游流域表层土壤氢氧稳定同位素空间分布模拟[J].应用生态学报，2021，32（12）：4327-4338.

收稿日期： 2023-06-30

基金项目： 国家自然资源和地理空间基础信息库安徽省试点项目

第一作者： 孙京禄（1986—），男，安徽淮南人，助理研究员，硕士，主要从事地理信息系统工作。

E-mail： Jinglusun@126.com

（责任编辑李佳星）