云环境下加密图上top-k 最近模糊关键词查询
潘瑛颖
(福建师范大学 计算机与网络空间安全学院,福建 福州 350117)
0 引言
图数据在许多领域得到广泛应用,如社交网络、知识图谱等。 随着云计算的快速发展,数据拥有者倾向于将大规模图数据外包给云服务器以降低存储和管理成本,但数据隐私泄露的风险也由此增加。 为保护数据隐私,数据拥有者需要在外包前对图数据进行加密,同时保留一定的隐私查询能力。
2010 年,Chase 等[1]引入结构化加密的概念并提出支持图的邻居查询、邻接查询和标记图上聚集子图查询的结构化加密方案。 此后,一系列支持近似或精确最短距离查询[2-3]、约束最短距离查询[4]、最短路径查询等功能的图加密方案先后提出[5]。 Liu 等[6]提出了支持top-k 最近关键字查询的图加密方案,查询距离给定节点最近的k 个具有给定关键词的节点,是一类重要的图查询应用。 但是,该方案针对精确关键字的提出,缺乏对细微的文字拼写错误的容忍,在一些场景下不能满足应用的需要。 在此基础上,本文提出支持在加密图上进行top-k 最近模糊关键词查询的图加密方案,该方案基于2-Hop 标签技术构造加密的2-Hop 标签索引,使用基于通配符的方法为关键词生成模糊集,构造模糊关键词索引,可以在出现细微拼写错误的情况下,返回距离给定节点最近的k 个可能被想要的关键词标记的节点。
1 符号定义和系统模型
1.1 符号定义
本文的符号定义如表1 所示。 SKE=(Gen,Enc,Dec)是一个对称加密方案,包括密钥生成算法SKE.Gen、加密算法SKE. Enc 和解密算法SKE. Dec,在选择明文攻击下具有伪随机的密文,满足CPA 安全。无向标记图G=(V,E,W)由顶点集V、边集E 和关键词字典W 组成,对于关键词w,W[w]存储被w 标记的顶点的集合。

表1 符号定义
1.2 系统模型
本文方案支持在加密的标记图上进行top-k 最近模糊关键词查询,标记图的各个节点被若干关键词标记。 方案的系统模型包括两个实体:用户和云服务器。 用户将原始图数据转换成加密索引外包给云服务器;用户将查询令牌T 发送给云服务器;云服务器执行查询算法获得加密结果R 并返回给用户。 R 由k个节点密文组成,用户解密R 得到明文结果。 具体如图1 所示。
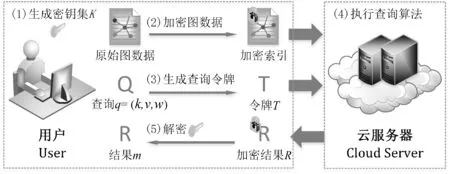
图1 系统模型
本文提出的支持top-k 最近模糊关键词查询的图加密方案包括5 个算法,形式化定义如下。
定义1. 一个支持top-k 最近模糊关键词查询的图加密方案Π 是一个包括5 个算法的元组Π =(KeyGen, Encrypt, Token, Query, Decrypt)。
(1)K←KeyGen(1λ):密钥生成算法,输入安全参数λ,输出密钥集K。
(2)I←Encrypt(K,G):加密算法,输入密钥集K和图G,输出加密索引I。
(3)T←Token(K,k,v,w):令牌生成算法,输入密钥集K,整数k,节点v 和关键词w,输出令牌T。
(4)R←Query(I,T):查询算法,输入加密索引I和令牌T,输出加密结果R。
(5)m←Decrypt(K,R):解密算法,输入密钥K 和加密结果R,解密得到明文结果m。
1.3 安全模型
图加密是结构化加密的一种,因此本文修改使用Chase 等[1]提出的自适应选择查询攻击安全性定义,即CQA2-安全性定义。 云服务器是诚实但好奇的,本文中被认为是敌手A。 泄露函数Λ1和Λ2分别表示存储在云服务器的加密数据泄露的信息和云服务器接收令牌查询的过程的泄露。
定义2. (CQA2-安全性)方案Π = (KeyGen,Encrypt, Token, Query, Decrypt)是一个图加密查询方案,Λ1和Λ2是方案的两个泄露函数。 给定安全参数λ,半诚实敌手A 和模拟器Σ 执行的两个概率性实验Real 和Ideal,定义如下。
(1)RealA(λ):敌手A 选择一个图G 发送给挑战者。 挑战者生成密钥K←KeyGen(1λ),计算加密索引I←Encrypt(K,G)返回给A。 A 生成多项式数量的自适应查询发送给挑战者。 对于每个查询(k,v,w),挑战者生成令牌T←Token(K,k,v,w)发送给A,A 运行Query(I,T)获得R。 最后,A 返回b∈{0,1}作为Real实验的输出。
(2)IdealA,∑(λ):A 选择图G。 给定泄露函数Λ1(G),Σ 模拟得到加密索引I∗发送给A。 A 生成多项式数量的自适应查询。 给定泄露函数Λ2,对于每个查询q,Σ 获得Λ2(I,Q),根据Λ2(I,Q)模拟令牌T∗返回给A,A 运行Query(I∗,T∗)获得模拟查询结果R∗。 最后,A 返回b∈{0,1}作为Ideal 实验的输出。
如果对所有概率多项式时间(Probabilistic Polynomial Time,PPT)敌手A,存在PPT 模拟器Σ满足:
| Pr[RealA(λ) = 1] - Pr[IdealA,S(λ) = 1] |≤negl(λ)
negl(λ)是一个可忽略函数,则方案Π 对于自适应选择查询攻击是(L1,L2)-安全的。
2 相关技术
2.1 2-Hop 标签
2-Hop 标签是一种预生成的快速计算两节点间最短距离的索引结构[7]。 给定无向图G=(V,E),L是图G 的2-Hop 标签,则L 为每个节点v 分配标签集L(v)。 L(v)是(u,d)对的集合,u 表示共享节点,d 表示u 和v 之间的最短距离。
对于任意两个可达顶点s 和t,存在至少一个节点u,使2-Hop 标签满足:(1)(u,d1)∈L(s),(u,d2)∈L(t);(2)u 在s 和t 之间的最短路径上。 因此,对于任意两个可达节点s 和t,可使用以下公式在L 上回答s 和t 之间的最短距离查询distQ(s,t,L)。
distQ(s,t,L)=min{d1+d2| (u,d1)∈L(s),(u,d2) ∈L(t)}
如果L(s)和L(t)没有共享节点,则distQ(s,t,L)=∞。 如果对任意s 和t,最短距离dst=distQ(s,t,L)成立,则L 是G 的一个2-Hop Cover。
本文使用Akiba 等[8]提出的剪枝地标标签(Pruned Landmark Labeling,PLL)算法生成2-Hop 标签。 PLL 算法对每个节点使用剪枝的BFS 构造2-Hop 标签索引。 如图2 所示展示了一个无向图的2-Hop 标签。

图2 2-Hop 标签示例
2.2 改进的保序编码
在2-Hop 标签索引上计算两节点间最短距离,需要再进行一次加法运算后进行值的比较。 Liu 等[6]改进的保序编码算法OPE 满足这一要求。 输入正整数密钥K3和整数d,OPE 将d 编码为D←K3·d+r,其中r 是(0,K3/2)内的随机数。
对于任意4 个整数值d1,d2,d3和d4,保序编码分别为Ddi←OPE(K3,di),i=1,2,3,4。 如果(d1+d2)>(d3+d4),那么(Dd1+Dd2)>(Dd3+Dd4)成立。
2.3 基于通配符构造模糊集
Li 等[9]利用编辑距离衡量两个关键词的相似性,并在此基础上提出一种基于通配符的方法构造模糊集。 编辑距离是指将一个单词转换为另一个进行替换、删除或插入一个字符3 种操作所需的次数。 基于通配符的方法使用通配符“∗”表示同一位置的一次编辑操作。 给定关键词w,Sw,ed是关键词w 的编辑距离≤ed 的模糊集,Sw,ed第一个元素是w 本身。 例如,令ed=1,art 的模糊集为Sart,1={act,∗art,∗rt,a∗rt,a∗t,ar∗t,ar∗,art∗}。
3 方案设计
本节对提出的标记图上top-k 最近模糊关键词搜索的图加密方案Π=(KeyGen, Encrypt, Token,Query, Decrypt)的各个算法进行详细介绍。
(1)K←KeyGen(1λ):密钥生成算法由用户执行,输入安全参数λ,生成λ-bit 随机字符串K1和K2作为伪随机函数P 的密钥,生成OPE 的密钥K3←Ζ2
λ,生成对称密钥K4←SKE. Gen(1λ),密钥集K=(K1,K2,K3,K4)。
(2)I←Encrypt(K,G):加密算法用户执行,输入密钥K,给定无向图G=(V,E,W),生成加密的图索引I=(DX1,DX2),包括一个加密的2-Hop 标签索引DX1和加密的模糊关键词索引DX2。 加密算法包括两个子算法HopIndex 和KeywordIndex,HopIndex 算法生成加密的2-Hop 标签索引,KeywordIndex 算法生成加密的模糊关键词索引。 如图3 所示,展示了一个加密索引示例,图3(a)是一个包含6 个节点、8 条边和3 个关键词的标记图,图3(b)和图3(c)分别是加密的2-Hop 标签索引和模糊关键词索引。
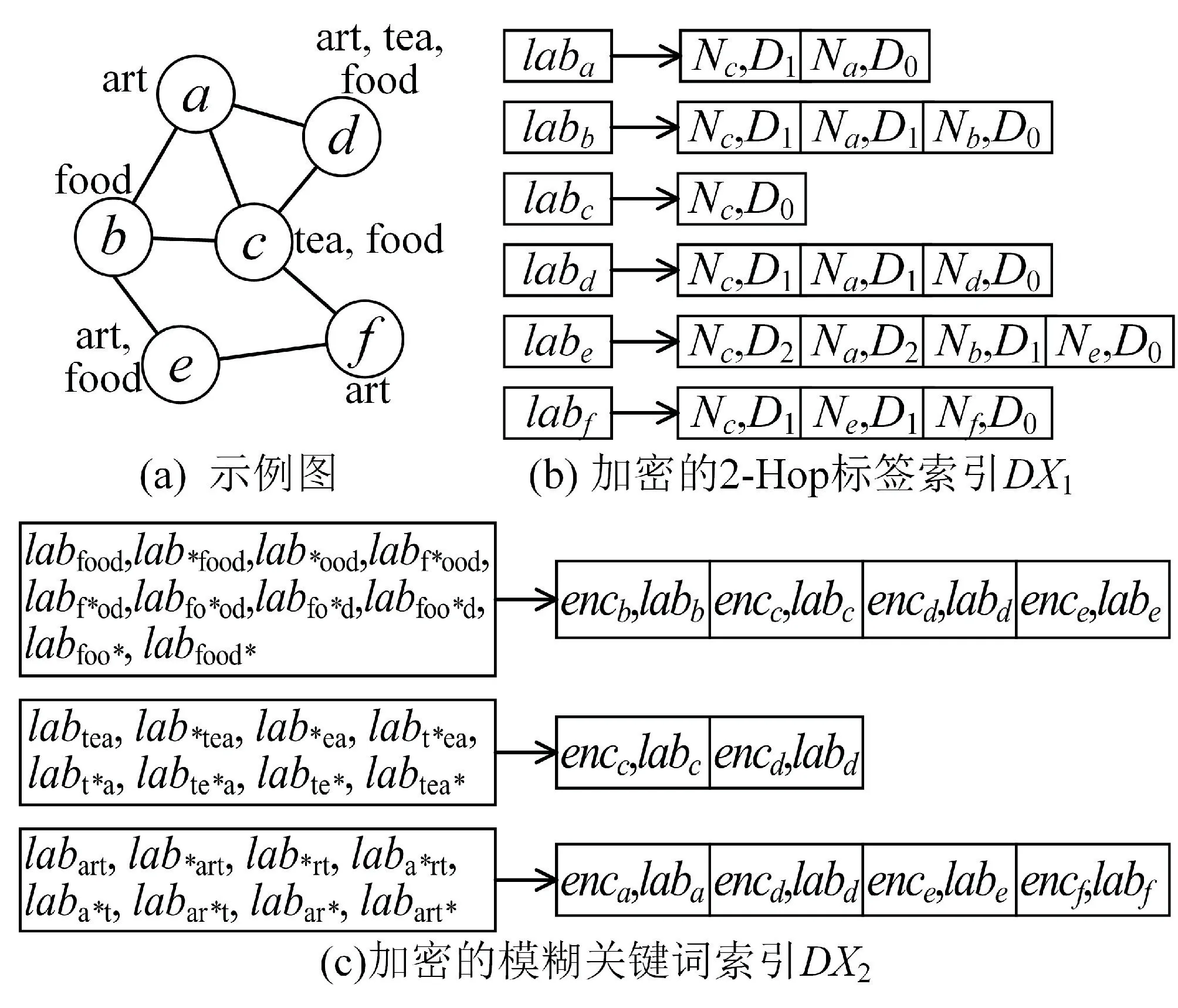
图3 加密索引示例
HopIndex 算法如算法1 所示,输入密钥集K=(K1,K2,K3,K4)和图G=(V,E,W),初始化DX1。 首先,使用Akiba 等[8]提出的PLL 算法计算图G 的2-Hop 标签L;然后,对L 加密,过程如下:先对图中的每个节点v,计算labv←P(K1,v‖′lab′)作为检索陷门,再对(u,d)∈L(v),计算Nu←P(K1,u‖′link′)隐藏真实的共享节点,并使用改进的OPE 算法加密距离d得到保序编码值Dd,将数据对? Nu,Dd? 插入Lv,Lv是L(v)的加密形式;最后,将键值对(labv,Lv)插入DX1。
算法1.DX1←HopIndex(K,G)
输入:密钥集K,图G=(V,E,W)
输出:加密的2-Hop 标签索引DX1
解析K 为(K1,K2,K3,K4),初始化DX1;
生成G 的2-Hop 标签索引L;
FOR v∈V DO
labv←P(K1,v‖′lab′);
初始化空集Lv;
FOR (u,d)∈L(v) DO
Nu←P(K1,u‖′link′),Dd←OPE(K3,d);
将
END FOR
将(labv,Lv)插入DX1;
END FOR
RETURN DX1.
KeywordIndex 算法如算法2 所示,输入密钥集K和图G=(V,E,W),生成加密的模糊关键词索引DX2。对于图G=(V,E,W)中出现的每一个关键词w∈W,首先,使用基于通配符的方法为其构造模糊集Sw,ed;然后,对于wt∈Sw,ed,计算保密值labwt←P(K2,wt‖′lab′)插入Labw,Labw是w 的加密模糊集;接着,对每个节点v∈W[w],使用SKE 加密v 得到密文encv,计算伪随机函数值labv←P(K1,v‖′lab′),并将
算法2. DX2←KeywordIndex(K,G)
输入:密钥集K,图G=(V,E,W)
输出:加密的模糊关键词索引DX2
解析K 为(K1,K2,K3,K4),初始化索引表DX2;
FOR w∈W DO
构造模糊集Sw,ed,初始化空集Labw和Lw;
FOR wt∈Sw,edDO
labwt←P(K2,wt‖′lab′),将labwt插入Labw;
END FOR
FOR v∈W[w] DO
encv←SKE. Enc(K4,v),labv←P (K1,v‖′lab′);
将
END FOR
将(Labw,Lw)插入DX2;END FOR
RETURN DX2.
(3)T←Token(K,k,v,w):令牌生成算法由用户运行,输入密钥集K=(K1,K2,K3,K4),整数k,节点v和关键词w。 首先,计算labv←P(K1,v‖′lab′);然后,为输入的关键词w 构造模糊集Sw,ed,并初始化一个空集Labw,对模糊集Sw,ed中的每个元素wi,计算labwi←P(K2,wi‖′lab′)并插入Labw,获得w 的加密模糊集;最后,算法输出查询令牌T=(k,labv,Labw)。
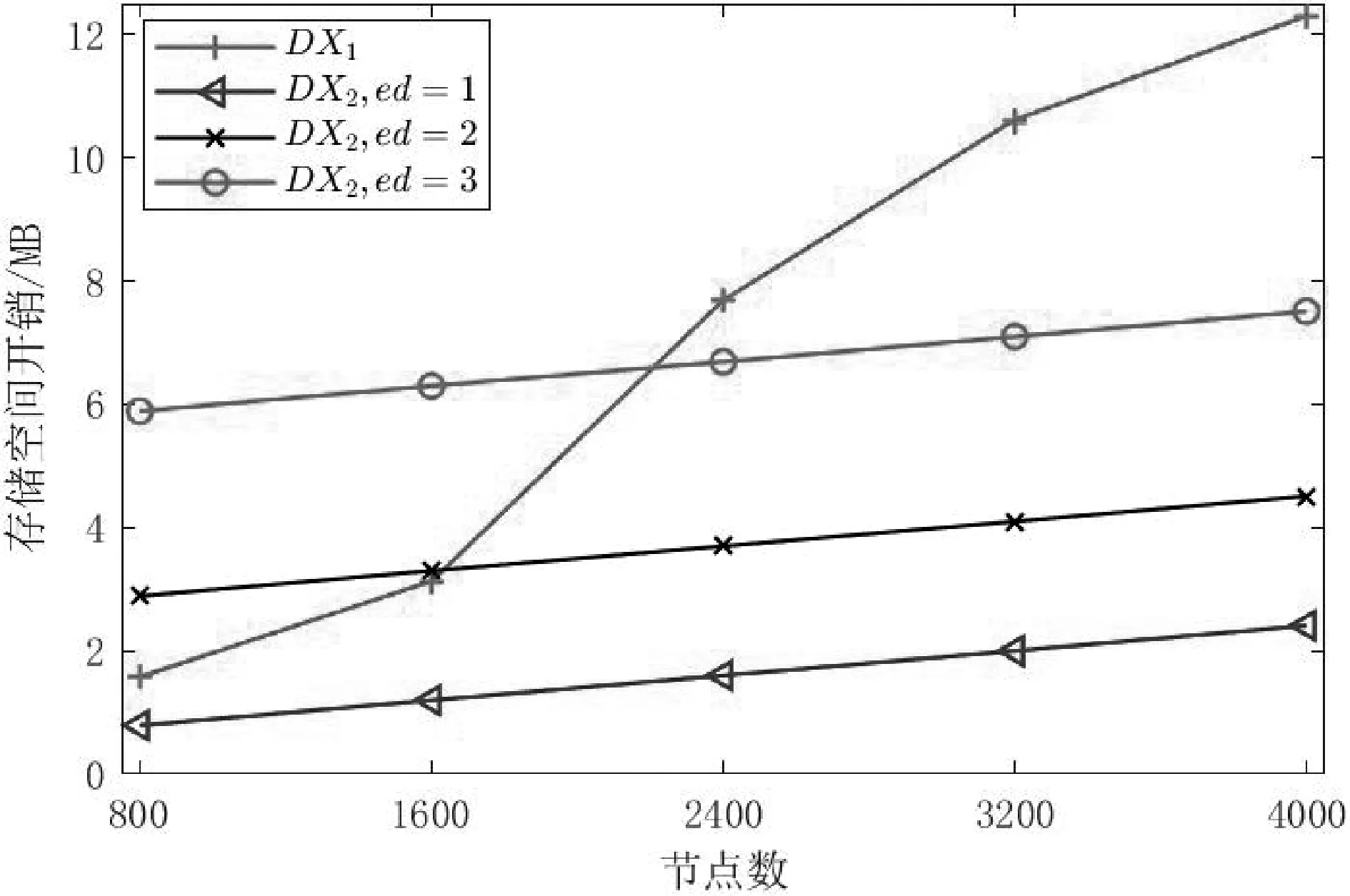
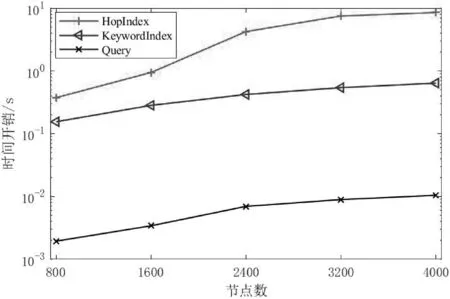
(4)R←Query(I,T):云服务器执行查询算法进行查询,过程如算法3 所示,解析令牌T 获得k,labv和加密模糊集Labw。 首先,借助labv从DX1获取给定节点v 的加密2-Hop 标签集。 初始化两个空集L′w和Temp 作为候选集。 比较Labw和DX2各条目中的加密模糊集Labwi,若两者交集不为空,则对应的加密节点集Lwi可能被用户想要的关键词标记。 从DX2中找出所有可能被关键词标记的保密数据项 算法3. R←Query(I,T) 输入:加密的图索引I,令牌T 输出:加密结果R 解析I 为(DX1,DX2),解析T 为(k,labv,Labw); Lv←DX2[labv]; 初始化空集L′w和Temp; FOR (Labwi,Lwi)∈DX2and Labw∩LabwiDO 检查每对 END FOR FOR Lu←DX2[labu]; Dvu←∞; FOR IF Ni= Njand Dvu> Di+ DjTHEN Dvu= Di+ Dj; END IF END FOR 将(encu, Dvu)插入Temp; END FOR 选取Temp 中距离编码值Dvu最小的k 个加密节点作为R; RETURN R. 如图4 所示,是一个查询过程示例。 查询距离节点e 最近的被art 标记的2 个节点,但在输入关键词时误拼写为artt。 图中生成的查询令牌T=(2,labe,{labartt,lab∗artt…labart∗,labartt∗})。 云服务器使用令牌T 在加密索引上进行查询。 第1 步,使用labe获取DX1中节点e 的加密标签集;第2 步,根据artt 的加密模糊集{labartt,lab∗artt…labart∗,labartt∗}检索可能包含想要关键词的加密节点项{(enca,laba),(encd,labd),(ence,labe),(encf,labf)};第3 步,在DX1中使用陷门获得a,d,e 和f 的加密标签集,分别计算e 到a,d,e和f 的最短距离编码;第4 步将加密节点-最短距离编码对插入Temp,选择最短距离编码最小的2 个节点密文ence和encf作为结果R。 图4 查询过程示例 (5)m←Decrypt(K,R):用户输入密钥K4和加密结果集R,依次对R 中保存的密文项使用SKE.Dec 解密,得到明文结果m。 本节简要分析两个泄露函数Λ1和Λ2,并证明提出的支持top-k 最近模糊关键词查询的图加密方案Π 满足CQA2-安全,即方案Π 对于自适应选择查询攻击是(Λ1,Λ2)-安全的。 泄露函数Λ1。 Λ1表示由存储在云服务器中的加密图索引I 存在的泄漏,定义Λ1(G)= {|V|,|W|,len1,len2,info},|V|和|W|分别是图的节点数和关键词数,len1和len2记录DX1和DX2中每个索引条目大小,info 泄露OPE 泄露的距离值顺序信息。 由于云服务器保存加密的2-Hop 标签索引,不泄露原始图的真实结构。 泄露函数Λ2。 Λ2表示查询过程引起泄露的信息。 设Q={q1,q2…qn}是一个非空查询序列,Λ2(I,Q)= {ΛQP(Q),ΛIP(I,Q)},包括查询模式泄露ΛQP(Q)和索引模式泄露ΛIP(I,Q)。 ΛQP(Q)揭示当前查询是否与已执行的查询存在重复,即查询的节点、关键词和整数参数k 的重复情况,由于使用伪随机函数对节点和关键词进行了混淆,不泄露真实的节点和关键词。 ΛIP(I,Q)揭示在查询过程中出现的泄露,包括两部分:(1)查询结果和查询过程访问了哪些索引条目;(2)查询过程中获取的索引内部关联情况,包括相同元素及部分距离顺序。 定理1. 如果P,OPE,SKE 是安全的,则方案Π即满足CQA2-安全。 证明:证明的主要思路是构造模拟器Σ,利用泄露函数Λ1和Λ2模拟索引I∗和查询序列Q∗。 如果敌手A 不能区分Real 实验和Ideal 实验,则认为方案满足CQA2-安全。 Σ 首先生成虚拟密钥集K∗←KeyGen(1λ),假定节点标识符和关键词。 模拟I∗:给定Λ1(G)= { | V|,| W|,len1,len2,info},Σ 在虚拟的密钥集、节点标识符和关键词上模拟构建加密索引I∗=(DX1 ∗,DX2 ∗)。 DX1∗包含|V|个条目,根据len1确定每个条目需包含的加密节点距离对的数量;DX2 ∗包含|W|个条目,根据len2确定模糊集中元素个数和对应节点集包含的节点密文数。 模拟Q∗:给定Λ2(I,Q)={ΛQP(Q),ΛIP(I,Q)},Σ 模拟查询令牌如下。 Σ 首先根据ΛQP(Q)检查待查询的节点和关键词和k 是否在之前的查询中出现过,如果是,使用先前的值;否则,Σ 根据ΛIP(I,Q)泄露的查询过程信息,选择模拟索引I∗中未使用过的对应项构造模拟令牌T∗。 由于伪随机函数P 具有伪随机的密文,OPE 只泄露顺序信息,SKE 是CPA 安全的,模拟的I∗和Q∗和真实情况不可区分, | Pr[RealA(λ) = 1] -Pr[IdealA,S(λ)= 1] |≤negl(λ) ,negl(λ)是一个可忽略函数,因此,方案Π 满足CQA2-安全。 本节对提出的方案进行实验评估。 实验在Intel(R) Core(TM) i7 CPU 2.30 GHz,16 GB 内存的PC上进行,利用Vmware 搭载开源项目OpenStack,使用Python 编程,选用斯坦福网络分析平台的ego -facebook 数据集进行测试,从中选取不同节点数的子图,选择500 个单词随机分配给各节点。 设安全参数λ=256,利用pycroptodome 库实现P 和SKE。 4.2.1 评估方案各阶段算法的存储开销 用户先生成4 个密钥,所需存储共128 B;构造加密的图索引I=(DX1,DX2)是一次性计算。 如图5 所示,展示在具有不同节点数的子图上,DX1存储开销和模糊集Sw,ed的参数ed=1,2,3 时,DX2存储开销变化。 DX1是加密的2-Hop 标签索引,存储和图的大小正相关;DX2存储在受图的大小影响的同时,ed 越大,关键词模糊集越大,所需存储空间越大。 图5 加密索引存储开销 4.2.2 测试方案各阶段的时间开销 KeyGen 算法生成4 个密钥,时间开销固定,在测试中低于0.1 ms。 令牌生成算法生成模糊集并计算若干伪随机函数,时间开销受模糊集大小影响,当关键词包含8 个字符且模糊集参数ed = 1 时,约为0.12 ms。 运行HopIndex 算法生成DX1、运行KeywordIndex算法生成DX2以及运行Query 算法进行查询所需时间如图6 所示。 HopIndex 算法生成2-Hop 标签并加密,所需时间与图的大小正相关; ed = 1 时,KeywordIndex 算法所需时间开销随图的规模增大而增大;在4 000 节点的子图上运行HopIndex 和KeywordIndex 算法,所需时间约为8.5 s 和0.64 s。查询所需时间主要受加密索引的大小影响,当节点数为4 000 时,查询所需时间为0.01 s,在实际应用中是可接受的。 图6 各阶段时间开销 4.2.3 分析方案的通信开销 用户完成对图数据的加密后,将加密的图索引发送给云服务器,这一过程是一次性操作,通信开销与加密图数据的存储开销一致。 在查询过程中,用户和云服务器之间的通信包括用户发送令牌给云服务器和云服务器返回加密结果给用户两部分。 本方案的令牌包括一个整数k 和若干λ 位伪随机函数值,在仅考虑ed=1 时,若关键词长为8,通信开销约为1.19 KB。 在云服务器将加密结果发送给用户的过程中,通信开销与k 有关,返回k 个SKE 加密的密文所需通信开销为16 KB。 本文提出一个在加密图上进行top-k 最近模糊关键词查询方案。 结合基于通配符的方法和2-Hop标签技术构造图索引并对标记图数据加密,利用OPE的性质对距离值进行比较,找出距离给定节点最近的可能具有所需关键词k 个节点。 安全性和实验评估表明本文方案是安全高效的。 然而,现实中各种网络往往是动态变化的,未来将进一步研究动态图的加密搜索,并将继续丰富本文方案的设计,使其支持更复杂的功能。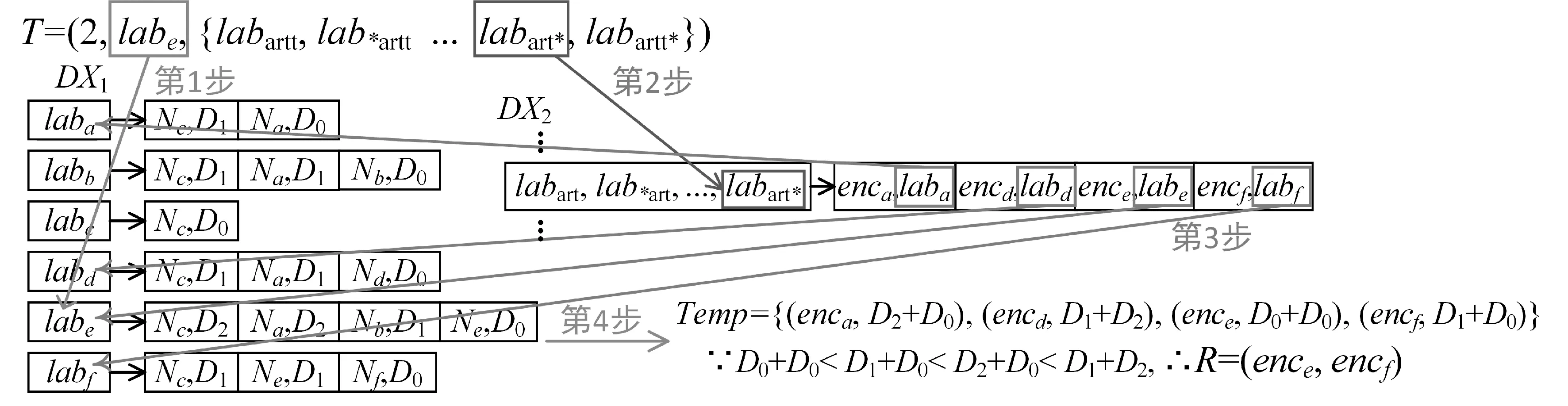
4 安全性分析和性能评估
4.1 安全性分析
4.2 性能评估
5 结语

