免支撑工具式桁架叠合板受弯性能试验研究与分析

张 旭，庞祖杰，王少杰，乔德浩，尹 烁，李 辉，张中文

(1.山东农业大学水利土木工程学院，山东，泰安 271018；2.山东高速德建集团有限公司，山东，德州 253000；3.东南大学土木工程学院，江苏，南京 210096)

混凝土叠合板是现代工业化建筑楼面结构体系中最常用的结构形式之一，由预制底板和上部后浇混凝土层叠合而成[1]，围绕其受弯性能已取得许多试验研究[2− 7]及数值或理论分析[8− 14]成果。然而，由于普通混凝土叠合板预制底板较薄(通常仅50 mm～70 mm)且上部桁架钢筋难以提供足够的抗弯刚度[15]，即使在吊装、运输等环节采取专用支架等措施仍难以完全避免预制底板易开裂问题，尤其是在施工期间依靠预制底板自身更难以承受各类施工荷载，从而使得叠合板施工现场如同现浇施工场地，仍需架设大量竖向支撑，不仅增加了施工成本、延长了工期，且不符合装配化施工特点。

为了显著减少甚至避免普通混凝土叠合板在施工全过程对竖向支撑的使用，吴方伯等[16]通过在板底设置可拆卸桁架代替竖向支撑，有效解决了底板开裂及施工期间受荷难题，置于板底的桁架可重复使用但拆除略显不便且拆除桁架后板底会有螺孔所致不平整现象。为此，借鉴钢-混凝土组合结构理念，通过在板顶设置混凝土肋[17−18]、钢肋[19− 21]等措施提高预制混凝土底板的受弯性能，除上述加肋措施外，在板顶设置灌浆钢管[22]、特殊材料或构件[23− 24]等措施也取得了良好效果，然而上述减少或免除支撑的措施多在浇筑后浇混凝土层时永久留在叠合板内部，无法作为工具重复使用。为了实现免支撑措施像工具一样可重复使用，项目组在前期研发了耳板式空腹桁架免支撑叠合板[25]并开展了试验研究，结果表明上部钢管始终处于弹性阶段并能重复使用，但在耳板区未被上部钢管覆盖的外围区域存在剪切失效风险，且耳板造价高不便于切除；进一步地，通过优化提出在端部设置斜筋代替耳板的策略，不仅可以降低造价，且斜筋可不切割或便于切割，还能通过端部斜筋覆盖区开裂避免跨中裂缝出现或减小跨中区域缝宽。

为此，首先通过3 个跨度相同端部斜筋覆盖区构造措施不同的免支撑工具式桁架叠合板试验，研究绑扎搭接、焊接、钢丝网片等构造措施对免支撑叠合板受力性能的影响；在明晰端部斜筋覆盖区构造措施基础上，综合运用试验研究和数值分析相结合的手段，研究不同跨度的免支撑工具式桁架叠合板的受弯性能与受力机制。最后，基于叠加原理，建立了精度高且具有明确物理意义的适于免支撑工具式桁架叠合板抗弯刚度和挠度计算的理论方法。

1 试验概况

1.1 试件设计与制作

与普通叠合板不同，工具式桁架叠合板在装配施工过程中可免除竖向支撑，如图1 所示其由下部混凝土底板、上部钢管以及连接二者的竖向连杆和位于两端部区域的斜筋等组成。为了探究两端斜筋覆盖区构造措施对免支撑工具式桁架叠合板受力及抗裂性能的影响，设计制作了3 个跨度方向均为3.6 m 长的试件，根据斜筋水平段与底板纵筋按照正常绑扎搭接(搭接长度220 mm)、焊接及在纵筋下侧增设钢丝网片(网格大小30 mm×30 mm)，分别命名为试件SM以及SM焊、SM网；在探明上述构造措施影响后，为探究不同跨度工具式桁架叠合板的受弯性能，以3.6 m 长绑扎搭接试件SM为参照，设计制作跨度方向分别为2.7 m和4.5 m 长的试件SS和SL。

图1 试件形式 /mmFig.1 Specimen form

各试件底板均为50 mm 厚、宽均为1.0 m，跨度、板宽方向钢筋布置分别为 8@150 和 8@300且均为HRB400 级；竖向连杆采用M14 螺杆与预埋在底板内的内螺纹套筒连接，内螺纹套筒下端有一长300 mm、直径为8 mm 的水平钢筋从纵筋下侧穿过；两端斜筋下部水平段按照前述构造措施与底板纵筋采用绑扎或焊接连接、上部焊有螺帽通过1 根M18 的水平螺杆与上部钢管相连；上部钢管均采用截面为矩形的空心钢管(截面尺寸b×h×t=60 mm×80 mm×5 mm)，钢管为Q235 级镀锌钢管，间距均为0.5 m，试件SS、SL及SM系列对应的钢管长度分别为2.3 m、4.1 m 和3.2 m，各试件详细尺寸如表1 所示。制作时钢管采用专用临时支架固定，待钢筋绑扎和各部品组装完成后，采用C30 商品混凝土浇筑并在专用模台上振捣制作底板。待底板混凝土强度达到设计强度后，连同上部可周转使用的工具式钢管，完成后续试件的转场、吊装运输、叠合施工(或试验加载)等；工程应用时当后浇叠合层达到设计强度后，拆除上部钢管即可，试验时混凝土实测强度为39.3 MPa。

表1 试件详细尺寸Table 1 Detailed dimensions of the specimens

1.2 加载制度

试件两端通过滚轴支座简支，端部支承长度均为100 mm。试验采用标准砝码均布加载[26]，前8 级采用单个重25 kg 的砝码，之后单个砝码的重降为20 kg。加载时砝码放置位置及顺序如图1 所示，按照B 奇C 偶、B 偶C 奇、A 奇D 偶、A 偶D 奇顺次交替进行，试件SS、SL及SM系列每级放置的砝码分别为8 个、10 个和10 个，前8 级各级对应的面荷载分别为0.78 kN/m2、0.57 kN/m2和0.72 kN/m2，第9 级及以后各级对应的面荷载分别为0.63 kN/m2、0.46 kN/m2和0.58 kN/m2。同条件养护试块达到设计强度后开始试验加载，正式加载前先进行预加载，预加载共分两级；之后，卸去砝码并清零，进行正式加载，各级均待在跨中板底布置的百分表读数稳定后再观察试验现象并采集应变、变形等数据，加载现场如图2 所示。

图2 试验加载现场Fig.2 Test loading site

1.3 数据采集

试验时采集各试件在各级荷载作用下对应的挠度、应变及试验现象等，试件SS、SM系列竖向变形测点分别布置在跨中、四分点和两端支座处(试件SL布置在跨中、六分点和两端支座处)，均通过电测位移计采集；各试件混凝土应变测点主要布置在底板跨中断面的板底、板顶及板的两侧，钢筋应变测点主要布置在两端斜筋覆盖区相邻的竖向连杆及斜筋中点处，具体方向为竖向连杆的左右侧和斜筋上下侧。通过uT8516 数据采集仪采集应变和变形，通过ZBL-F103 裂缝测宽仪测试缝宽，在对应方格纸上记录裂缝开展等试验现象。图3 为SM系列试件的变形和应变测点布置图。

图3 测点位置 /mmFig.3 Measuring point position

2 试验结果与分析

2.1 试验现象

2.1.1 构造措施

图4 为相同跨度(3.4 m)不同构造措施的3 个试件SM、SM焊、SM网的裂缝在板底及板两侧面的分布图，显然裂缝主要集中分布在两端斜筋覆盖区和跨中区域，各试件板底裂缝均未贯穿至板顶且板顶混凝土未见压碎，钢管、竖向连杆及斜筋均未见屈曲。试验数据分析可得，试件SM、SM焊、SM网对应的开裂荷载分别为4.32 kN/m2、3.60 kN/m2、5.04 kN/m2，分别位于端部斜筋覆盖区、跨中、跨中，缝宽分别为0.02 mm、0.02 mm 和0.08 mm；竖向荷载加载至最大试验荷载9.80 kN/m2时，各试件对应的最大缝宽分别为0.20 mm、0.37 mm 和0.16 mm，跨中挠度分别为27.1 mm、28.0 mm 和28.9 mm；卸除上部荷载后，各裂缝基本均闭合，最大残余缝宽分别是0.08 mm、0.08 mm 和0.03 mm，跨中残余变形分别是7.3 mm、8.8 mm 和6.7 mm。综上，斜筋覆盖区采取焊接措施对应的试件SM焊开裂最早且残余变形、残余缝宽均最大，采取增设钢丝网片能推迟首条裂缝出现并降低残余变形和残余缝宽，但最大挠度在3 个试件中最大。故，考虑加工制作的方便性和构造措施的实际效果，建议在斜筋覆盖区仍采用斜筋水平段与相应纵筋绑扎搭接构造措施。

图4 试件SM 系列的裂缝分布图Fig.4 Crack distribution diagram of specimen SM series

2.1.2 跨度

图5 为试件SS、SL的裂缝分布图，结合图4(a)所示试件SM的裂缝分布对比分析可知：裂缝分布特征与跨度紧密相关，以跨度较小的试件SS为例，裂缝全部分布在两端斜筋覆盖区，跨中区域无裂缝；中等跨度试件SM裂缝仍以两端斜筋覆盖区为主，但跨中亦有少量裂缝；跨度较大试件SL的裂缝分布已演化为跨中区域为主的特征。定量分析可知，试件SS、SM、SL对应的开裂弯矩分别为4.90 kN·m、6.24 kN·m 和6.59 kN·m，此时首条裂缝缝宽分别为0.02 mm、0.02 mm 和0.04 mm，对应的挠度分别为5.1 mm、8.9 mm 和13.0 mm；各试件施加至试验荷载最大值对应的弯矩分别是8.09 kN·m、14.16 kN·m 和14.75 kN·m，此时对应的最大缝宽分别为0.23 mm、0.20 mm 和0.14 mm，跨中挠度分别为10.6 mm、27.1 mm 和36.5 mm。综上可知，三种跨度的免支撑工具式桁架叠合板均在两端斜筋覆盖区存在开裂现象，伴随跨度增加底板跨中区方逐渐出现裂缝，破坏特征的不同对应受力机理的不同，小跨度试件除两端斜筋覆盖区外中间区域无开裂现象，底板与上部钢管的轴向变形一致，二者之间在跨中未开裂区域基本无剪切变形；当底板跨中区域开裂后，等同于开裂区底板被拉长，从而与上部钢管之间需要依靠竖向连杆及节点的剪切变形实现变形协调，故底板与钢管之间的桁架作用得到显现且贡献随挠度和跨度的增大而增大。

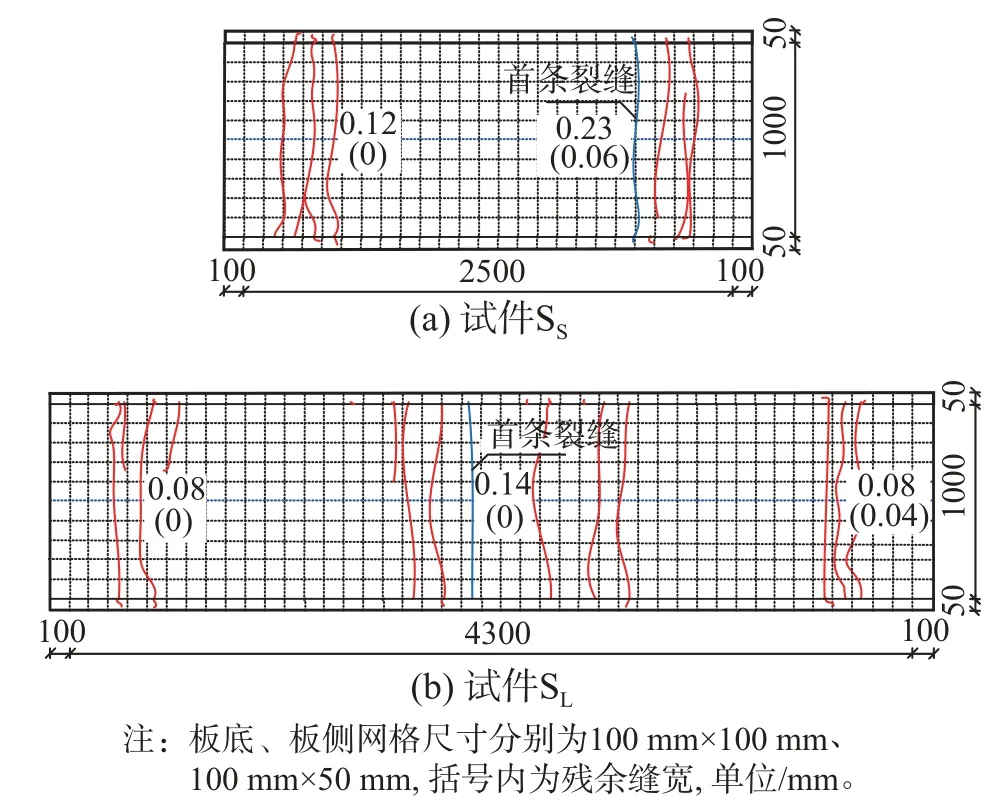
图5 试件SS、SL 的裂缝分布图Fig.5 Crack distribution diagram of specimen SS and SL

2.2 跨中弯矩-变形曲线

图6 为各试件跨中弯矩-变形关系曲线，可明显看出以开裂为界具有两阶段特征。开裂前，跨中变形伴随荷载增加近似呈线性增长；开裂后曲线斜率逐渐减小，挠度增长速率加快。由图6(a)可知，构造措施对跨度相同的3 个试件SM、SM焊、SM网的跨中弯矩-变形曲线无显著影响，趋势完全相同；定量对比分析可知，至施加的竖向面荷载最大值9.80 kN/m2时，试件SM、SM焊、SM网对应的跨中变形分别是27.1、28.0 和28.9 mm，卸除荷载后残余变形分别是7.3、8.8 和6.7 mm，显然斜筋覆盖区配置钢丝网片能降低残余变形但峰值变形以试件SM为最小。图6(b)为不同跨度的免支撑工具式桁架叠合板的跨中弯矩-变形曲线，显然伴随跨度增加在上部钢管规格相同的情况下试件开裂提前，对应第1 阶段缩短；跨中截面弯矩相同时，对应的挠度伴随跨度的增加而增加，以弯矩5.2 kN·m 为例，试件SS、SM和SL对应的挠度变形分别是6.2 mm、6.6 mm 和9.4 mm。

图6 跨中弯矩-变形关系曲线Fig.6 Mid-span moment-deformation relation curves

2.3 工作机制

因两端斜筋覆盖区对免支撑工具式桁架叠合板的受弯性能无显著影响，遂以跨度不同的试件SS、SM和SL为对象，通过上部钢管、下部混凝土底板及二者间竖向连杆及端部斜筋的实测应变探究免支撑工具式桁架叠合板的受力机制。

图7、图8 分别为不同跨度的免支撑工具式桁架叠合板在相应面荷载作用下上部钢管、下部混凝土底板跨中截面沿截面高度的实测应变分布。

图7 各试件钢管跨中截面实测应变Fig.7 Measured strain of mid-span section of steel tube of each specimen

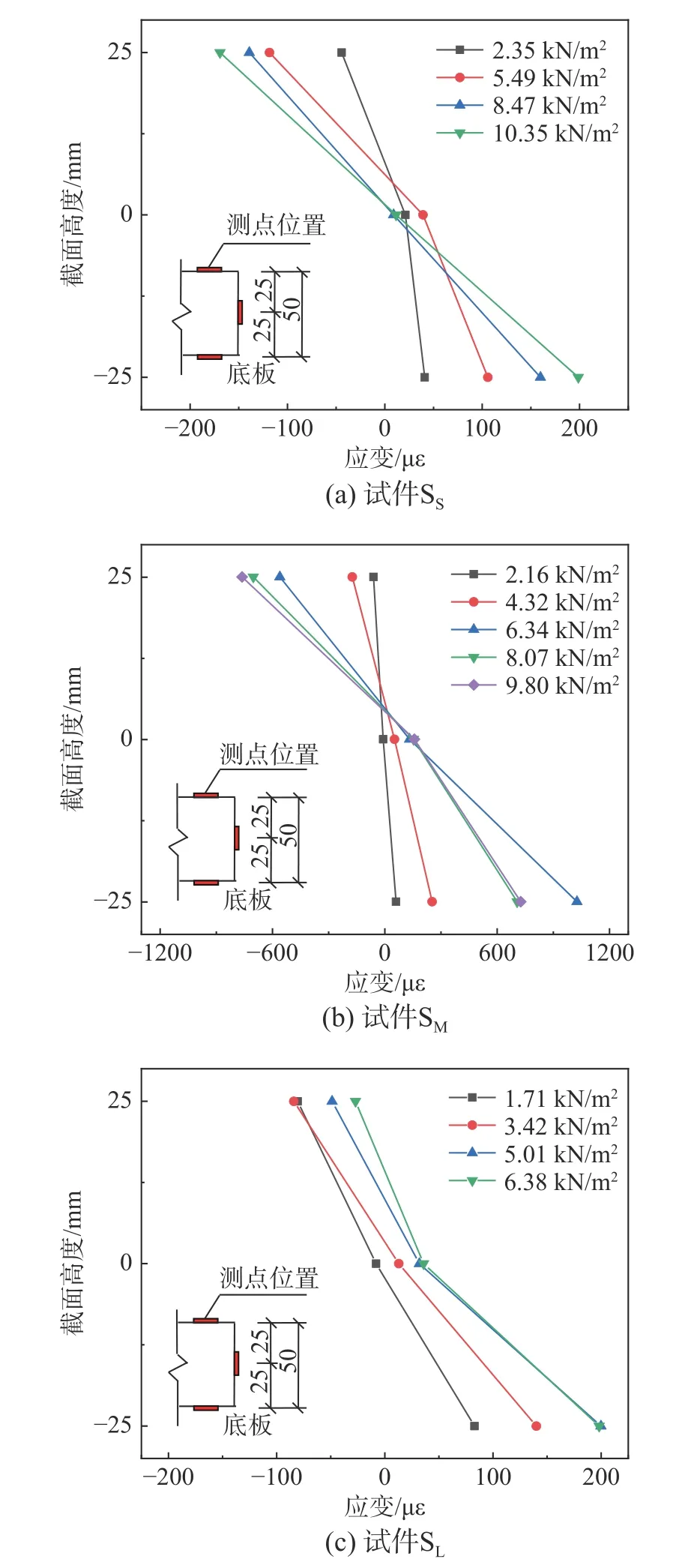
图8 各试件混凝土底板跨中截面实测应变Fig.8 Measured strain of mid-span section of concrete bottom slab of each specimen

由图7 可知，试件SS、SM和SL上部钢管为典型的受弯构件，截面上侧受压、下侧受拉，各级荷载下的拉、压应变绝对值大致相等且最大拉、压应变均小于屈服应变(1175 µε)，钢管均处于弹性受力阶段；由图8 可知，下部混凝土底板应变沿截面高度的分布规律与上部钢管类似，亦呈上部受压、下部受拉弯曲特性，但拉应变值较压应变值略大，至混凝土底板开裂后拉压应变沿截面高度的分布对称性变差。

由前文分析可知，免支撑工具式桁架叠合板受弯性能以开裂为界具有明显的两阶段特征且各阶段均近似呈线性特性。为探究上部钢管与下部混凝土底板之间的竖向连杆和端部斜筋的工作机制，并考虑试件SS、SM和SL的跨度不同，分别针对开裂前后选取跨中截面弯矩大致相等时竖向连杆及端部斜筋的实测应变开展对比分析。如图9所示，其中，试件SS、SM、SL在开裂前和开裂后对应的弯矩分别是4.29 kN·m、4.16 kN·m、3.95 kN·m和6.62 kN·m、6.24 kN·m、6.59 kN·m。分 析 可知，各试件的竖向连杆及端部斜筋的实测应变在底板开裂后较开裂前均显著增大，但底板在跨中区域未开裂试件SS的应变值在开裂前后均明显低于试件SM和SL且应变较小。究其原因是当底板跨中区域开裂后方会产生明显的拉伸变形，在底板被拉长的同时上部钢管的变形较小，使得与二者相连的竖向连杆、端部斜筋产生剪切变形并提供抗弯刚度；与之相反，如果底板在跨中区域未见明显开裂，上部钢管与下部底板间的剪切作用则较小，甚至可以忽略二者间的剪切变形对抗弯刚度的贡献。

图9 不同跨度试件腹杆实测应变对比Fig.9 Comparison of measured strains of the specimens with different spans

3 数值分析

3.1 数值模型

通过建立精细化的有限元模型开展数值分析，不仅能进一步直观展示和探究免支撑工具式桁架叠合板的受力特点，而且可以用于拓展分析。以试件SM为例详述建模过程，图10 为基于ABAQUS 软件建立的数值模型，混凝土底板上表面嵌有套筒，上部钢管与底板间通过竖向连杆螺栓连接，斜筋通过水平螺栓与钢管相连，斜筋下部水平段内嵌于底板内。其中混凝土底板、钢管、螺栓、套筒均采用C3D8R 六面体实体单元，钢筋采用T3D2 三维桁架单元，混凝土底板单元长度为25 mm，水平螺栓、竖向连杆与套筒的单元长度均为5 mm，斜筋及板内钢筋的单元长度为10 mm，钢管在长度和截面方向的单元长度分别为80 mm、20 mm，并对各圆孔处网格加密。在处理各组成部件的相互作用时，对于埋在混凝土板内部的钢筋网、斜筋及与竖向连杆相连接的套筒，均采用内置方法；竖向连杆与钢管、水平螺杆与钢管等接触面，均采用面与面接触并考虑滑移；板两端分别采用固定铰支座和可动铰支座作简支处理，并考虑竖向连杆预紧力的影响。考虑混凝土拉伸效应，混凝土采用塑性损伤模型[27]；钢筋、钢管等金属部件均采用理想双折线模型[28]。边界条件同试验加载，两端分别设为固定铰和可动铰，支承长度均为100 mm。

图10 数值模型(试件SM)Fig.10 Numerical model (specimen SM)

3.2 模型验证与分析

通过跨中弯矩-变形曲线验证数值模型及分析结果可靠性，如图11 所示；图中解析解为依据下文建立的理论计算方法所得。可明显看出，虚线所示数值解与实测值变化趋势一致且吻合度高，试件SS、SM、SL的平均绝对误差(MAE)分别为0.303 mm、0.486 mm 和2.048 mm，决定系数(R2)分别为0.992、0.996 和0.988，数值分析结果可靠。

图11 数值解、解析解与实测值对比Fig.11 Comparison of the numerical and analytical solutions with the measured values

进一步地可得到试件SS、SM和SL的应力大小及分布云图。图12 为各试件混凝土底板板底拉应力云图，可以看出板底受拉，应力在竖向连杆对应位置较大且外侧大于内侧；端部斜筋覆盖区板底最大拉应力均超过C30 混凝土对应的抗拉强度标准值(ftk= 2.01 MPa)；跨中区域混凝土所受的拉应力伴随跨度增加而增大，试件SS、SM和SL在板底跨中区域对应的最大拉应力分别为0.49 MPa、2.21 MPa 和2.08 MPa，试件SM、SL对应值均大于2.01 MPa，与2.1 节所述试验现象吻合，亦进一步厘清了2.3 节所述不同跨度免支撑工具式桁架叠合板的受力机制。与此同时，还提取得到了试件SS、SM和SL上部钢管对应的最大拉、压应力分别是58.8 MPa、112.0 MPa、120.9 MPa 和36.3 MPa、81.1 MPa、88.3 MPa，显然上部钢管所受应力伴随跨度增加而增大，但均远低于屈服强度，钢管处于弹性工作阶段，可作为工具多次周转使用。

图12 不同跨度试件混凝土板底应力云图Fig.12 Bottom stress cloud diagram of concrete slab with different span

4 计算方法

4.1 理论推导

建立在前文对免支撑工具式桁架叠合板受弯性能和工作机制的探究基础上，可得到如图13 所示的理论计算模型，免支撑工具式桁架叠合板的整体抗弯刚度由上部钢管1)和下部混凝土底板2)的弯曲变形及二者间桁架剪切变形3)三部分组成，可采用叠加法计算。各部分提供的抗弯刚度计算方法如下：

图13 计算模型示意图Fig.13 Schematic diagram of calculation model

1)钢管

钢管始终处于弹性工作阶段，刚度计算采用式(1)：

式中：Es为钢管弹性模量；Is为钢管截面惯性矩。

2)混凝土底板

由2.2 节可知免支撑工具式桁架叠合板以混凝土底板开裂为界具有明显的两阶段特征，因此选用《混凝土结构设计规范》(GB 50010−2010)(2015 年版)[27]7.2.3 节预应力混凝土受弯构件短期刚度计算公式计算混凝土底板提供的刚度，分别如式(2)、式(3)：

开裂前：

开裂后：

式中：Ec为混凝土弹性模量；Ic为混凝土底板截面惯性矩；κcr为混凝土底板正截面开裂弯矩Mcr与受荷弯矩Mk的比值，当κcr>1.0 时，取κcr=1.0；Mcr为混凝土底板正截面的开裂弯矩，采用式(4)计算；系数ω采用式(5)计算：

式中：ftk为混凝土轴心抗拉强度标准值；W0为混凝土底板截面抵抗矩；αE为钢筋弹性模量与混凝土弹性模量的比值，即Es/Ec；ρ为纵向受拉钢筋配筋率；γ为混凝土底板的截面抵抗矩塑性影响系数，采用式(6)计算；h为混凝土底板截面高度，γm取1.55。

3)桁架部分

上部钢管与下部混凝土底板之间的桁架依靠剪切变形提供刚度，其剪切变形由竖向连杆伸缩变形 ∆brace和节点变形 ∆joint共同组成，节点包括T 形和K 形节点，如图13 所示。参照文献[29 − 31]提供的方法计算免支撑工具式桁架叠合板因桁架剪切变形提供的刚度Bt，如式(7)～式(9)：

式中：P为作用于混凝土底板上表面的竖向荷载；为单位荷载作用下的支撑轴力；Nw为竖向荷载P作用下的支撑轴力；lw为桁架连杆节段长度；El为连杆弹性模量；Aw为连杆横截面面积；K为桁架节点轴向刚度，T 型节点KT、K 型节点KK分别采用式(10)、式(11)计算：

式中：b0、h0分别为钢管的截面宽度、高度；t0为钢管的厚度；leff为钢管受连杆影响的有效长度，等于b0(0.65−0.65β) ，β为竖向连杆或斜筋的直径与上部钢管宽度b0之比；Ka、Kb分别采用式(12)、式(13)计算，其中h1为连杆高度、g为斜筋间距、θ为斜筋与钢管之间的夹角角度。

综上可得，免支撑工具式桁架叠合板的整体抗弯刚度B=Bs+Bc+Bt，其中，根据混凝土底板跨中区域是否开裂作为考虑桁架作用的依据，即跨中区域开裂考虑桁架作用、跨中区域未开裂则不考虑桁架作用。进而据公式(14)可得到距离支座为x处任意截面的挠度，l为叠合板跨度；当x=l/2时，即为跨中截面对应的挠度计算公式，见式(15)：

4.2 方法验证与分析

由图11 所示跨中弯矩-变形曲线对比分析可知，实线所示解析解与实测值吻合度高，误差较小。开裂前，试件SS、SM、SL解析解与实测值 之 间 的MAE 分 别 是0.181 mm、1.713 mm 和1.035 mm，且相同荷载作用下的挠度变形解析解均略大于实测值，工程应用偏于安全；开裂后，三者对应的MAE 分别是0.856 mm、2.781 mm 和1.970 mm，各试件加载全过程对应的决定系数(R2)均大于0.99。因此，建立的理论计算方法精度与可靠性均较高，且物理意义明确。

基于建立和验证的上述理论计算方法，开展免支撑工具式桁架叠合板在加载全过程刚度变化和演化规律的分析。由图14(a)可知，试件SS、SM、SL的总体抗弯刚度在开裂前保持不变，且SL>SM>SS，即叠合板跨度越大抗弯刚度越大；开裂后刚度下降呈先快后慢之势，试件SS、SM和SL在加载至峰值荷载时对应的抗弯刚度分别降至开裂前的81.5%、80.9%和83.0%。图14(b)为上部钢管、下部混凝土底板及二者间桁架剪切变形提供的刚度占比，显然在开裂前各部分的占比不变，且占比大小是钢管>底板>桁架；在加载全过程对免支撑工具式桁架叠合板整体抗弯刚度贡献最大的部分均是钢管，且钢管的贡献在试件开裂后进一步提高，至峰值荷载时试件SS、SM和SL的钢管刚度贡献占比分别是77.3%、68.4%和59.2%；底板对试件抗弯刚度的贡献伴随混凝土开裂呈显著下降趋势，桁架的贡献在底板开裂后有小幅增长，但其增幅低于底板降幅；因试件SS桁架贡献被忽略，对比分析SM、SL刚度占比可知，叠合板跨度越大桁架对其总体抗弯刚度的贡献越大，即跨度较小时桁架剪切变形对刚度的贡献作用较小甚至可以忽略。

图14 不同跨度试件刚度变化与演化Fig.14 Stiffness variation and evolution of the specimens with different spans

5 结论

本文研发了一种免支撑工具式桁架叠合板，通过模型试验、数值分析与理论计算相结合的方法，探明了免支撑工具式桁架叠合板的受弯性能与工作机制，主要结论如下：

(1)免支撑工具式桁架叠合板受弯性能以开裂为界具有明显的两阶段特征，由上部钢管、下部混凝土底板的弯曲变形和二者间的桁架剪切变形共同提供抗弯刚度，桁架剪切变形对抗弯刚度的贡献伴随跨度增加而增加(跨度2.5 m 时可忽略)；两端斜筋覆盖区采用焊接或增设钢丝网片等构造措施，对免支撑工具式桁架叠合板的整体受弯性能无显著影响，但钢丝网片会推迟首条裂缝出现并降低板底残余缝宽。

(2)通过建立免支撑工具式桁架叠合板的精细化模型开展数值分析，可以得到与实测值变化趋势一致且吻合度高的数值解(决定系数最小值为0.988)，为开展该类免支撑叠合板受力性能拓展分析提供了高效研究手段，亦直观展示了受力易损区，为该类叠合板设计制作提供了参考依据。

(3)免支撑工具式桁架叠合板的整体抗弯刚度可由上部钢管、下部混凝土底板和二者间桁架剪切变形三部分叠加，所建立的刚度与挠度理论计算方法，不仅精度高且物理意义明确。结果表明，免支撑工具式桁架叠合板整体抗弯刚度以开裂为界具有两阶段特征，开裂后刚度均呈先快后慢下降趋势(平均降幅18.2%)，且加载全过程均呈现为跨度越大整体抗弯刚度越大；在开裂前三种跨度不同的试件SS、SM和SL对抗弯刚度贡献大小均是钢管>底板>桁架，且钢管贡献伴随混凝土底板开裂进一步增大，至所施加的峰值荷载时分别增至77.3%、68.4%和59.2%；开裂后底板对刚度的贡献下降，桁架剪切变形对刚度的贡献上升，但其增幅较底板降幅小。