混合梁刚构桥钢-混结合段的构造优化与试验

陈德宝，林志平，苏庆田，欧阳明谷，上官兵

(1.同济大学土木工程学院，上海 200092；2.福建省高速路桥建设发展有限公司，福建，厦门 361002；3.中交泉州高速公路有限责任公司，福建，泉州 362343)

混合梁桥是指在纵桥向上由钢梁和混凝土梁通过钢-混接头有效连接并共同受力的桥梁结构[1]。目前，混合梁在梁式桥[2]、斜拉桥[3− 4]和悬索桥[5]等桥型中均有应用。自混合梁的结构形式被提出之后，国内外结合混合梁斜拉桥工程开展了大量的试验研究[6−8]，明确钢-混结合段的受力特性和屈曲性能[9−11]、不同连接件形式对结合段传力性能的影响[12−14]、结合段承压板对轴力的传递比例[15 − 16]和结合段的疲劳性能[17]等。邓文中等[18− 19]于21 世纪初提出了混合梁刚构桥的设计方案，并率先应用于重庆石板坡长江大桥复线桥(主跨330 m，2007 年)，此后，国内又陆续建成了瓯越大桥(主跨200 m，2015 年)、鱼山大桥(主跨260 m，2018 年)等几座混合梁刚构桥。

混合梁桥的钢-混接头作为连接钢梁与混凝土梁的局部构造，受力复杂，构造形式多样。钢-混接头在纵桥向上包括钢梁过渡段、钢-混结合段和混凝土梁过渡段[20]。主梁一般采用箱形截面，在钢箱梁顶板、底板和腹板分别布置钢格室并填充混凝土构成钢-混结合段。对于混合梁刚构桥，主梁为承受弯矩和剪力作用的构件，且由于钢-混接头处一般会布置局部预应力钢束，所以钢-混结合段的局部格室处于压弯剪受力状态。

针对混合梁刚构桥钢-混接头的受力性能，田军伟等[21]依托石板坡长江大桥复线桥设计方案，按1∶2 相似比设计钢-混结合段的半截面模型，对缩尺模型进行了静力加载和疲劳加载，试验结果证明实桥的设计是安全可靠的。曹学亮[22]以瓯越大桥为工程背景，设计相似比为1∶16 的全桥缩尺模型并进行静力加载，试验结果表明在12.68 倍的汽车活载作用下支墩处的混凝土发生破坏而钢-混接头处完好。上述试验研究没有得到混合梁刚构桥钢-混接头的极限承载力和实际破坏形态。由于钢-混结合段中有数量众多的钢板、焊钉和开孔板(PBL)连接件及预应力钢束，形状尺寸多变，构造极其复杂，目前的数值计算方法还无法真实地模拟其受力情况，无法准确地得到其极限承载力和破坏形态[23−24]。此外，钢-混结合段的结构尺寸较大，目前受加载能力的限制，足尺模型试验难以测得钢-混结合段的极限承载力。因此，开展混合梁刚构桥钢-混结合段局部构造的极限承载力和破坏形态的研究，对明确结合段的安全储备情况具有重要意义[25]。

近些年随着我国交通建设的迅猛发展，主跨120 m～300 m 的桥梁越来越多地采用混合梁刚构桥这一桥型[26]。调研发现，国内几座混合梁刚构桥的钢-混接头构造均参考石板坡长江大桥复线桥的设计方案，采用有格室后承压板式的钢-混结合段形式[27]。在明确现有混合梁刚构桥钢-混结合段的受力机理和安全储备的基础之上，开展结合段形式优化，提出结构简单、受力安全、施工方便的结合段构造，能够为推广应用混合梁刚构桥提供基础性资料。

基于混合梁刚构桥钢-混结合段的研究现状与应用前景，本文结合一座主跨300 m 的混合梁刚构桥实际工程，对其钢-混结合段开展极限承载力和破坏形态研究，并依据计算分析结果及工程施工的实际情况，优化结合段的构造形式，测试优化后构造的极限承载力与破坏形态，论证其可行性与安全性，为进一步推广混合梁刚构桥这一桥型提供有益的参考。

1 背景工程

1.1 工程概述

安海湾特大桥为三跨混合梁连续刚构桥，跨径布置为135 m+300 m+135 m，总体布置如图1所示。跨中钢箱梁吊装段长度为103 m，钢箱梁两端通过钢-混接头与混凝土箱梁连接。箱梁顶板宽16.25 m，底板宽7.65 m。混凝土箱梁的墩顶截面梁高15 m，钢箱梁跨中截面梁高4.5 m，梁高按2 次抛物线规律变化。钢材为Q345qD，混凝土强度等级为C55。

图1 安海湾特大桥总体布置 /cmFig.1 General layout of Anhai Bay Bridge

钢-混接头总体布置如图2 所示，采用有格室后承压板式的构造形式。顶部设置14 个钢格室，底部设置8 个钢格室，钢格室高1.2 m，钢格室的壁板上设置PBL 连接件和焊钉连接件。顶部钢格室上顶板厚26 mm，下底板厚25 mm；底部钢格室上顶板厚25 mm，下底板厚24 mm；腹板钢格室外侧板厚28 mm，内侧板厚25 mm；后承压板厚50 mm。焊钉尺寸为Φ22×200 mm，PBL 连接件孔径为70 mm，穿孔钢筋为Φ20 mm。图3 为钢-混结合段局部构造的三维示意图。

图2 钢-混接头总体布置 /mmFig.2 General layout of the steel-concrete joint

图3 钢-混结合段局部构造三维示意 /mmFig.3 Three-dimensional schematic diagram of local structures of a steel-concrete composite segment

1.2 钢-混结合段受力分析

为了分析钢-混结合段的局部受力性能，如图4所示，首先建立Midas 全桥分析模型，计算混合梁连续刚构桥在各项设计荷载作用下的最不利内力状态，然后建立钢-混结合段的Ansys 精细化有限元模型。基于圣维南原理，选取足够长的节段可以消除节段的边界条件对计算结果的影响，因此Ansys 节段模型全长取24 m，包括5.5 m 长的标准混凝土段，5.5 m 长的混凝土刚度过渡段，2.5 m长的钢-混结合段，6.5 m 长的钢箱梁刚度过渡段，4 m 长的标准钢箱梁段。在钢梁侧设置固端约束，在混凝土梁侧施加Midas 模型中提取的截面内力。Ansys 模型采用Shell181 单元模拟钢结构，Solid95 单元模拟混凝土，Link180 单元模拟预应力钢束，Combin14 单元模拟焊钉和PBL 连接件。

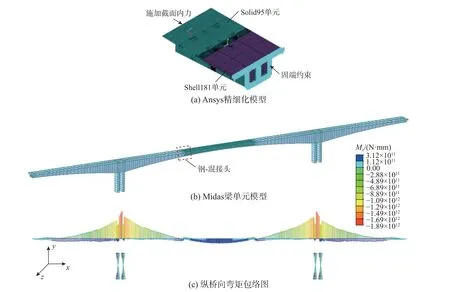
图4 钢-混结合段局部受力计算Fig.4 Local stress calculation of a steel-concrete composite segment

钢-混结合段在最不利的荷载工况组合下，各截面均受压，钢箱梁过渡段的应力大于钢格室的应力，说明在极限状态下钢箱梁过渡段会先于钢-混结合段破坏。钢-混结合段顶部钢格室的受力比底部钢格室的受力更为不利。因此，本文重点关注顶部钢格室的受力(图3 红色高亮部分为模型试验的原型)，将该部分单元的节点力求和得到钢-混结合段的设计轴向压力为8600 kN，设计竖向剪力为1000 kN。

1.3 钢-混结合段的初步优化

在钢-混结合段局部受力计算的基础上，建立局部钢格室的有限元模型，施加设计轴向压力，钢格室高度h分别为1.2 m、1.1 m、1.0 m、0.9 m和0.8 m，分析钢格室的传力规律和承担的轴力比例。

图5 给出了钢格室顶板的纵向应力变化规律。随着钢格室高度从1.2 m 减小至0.8 m，后承压板位置附近处的钢格室纵向应力峰值从−29.0 MPa增加至−36.7 MPa，表明钢格室高度减小33.3%，钢格室纵向应力峰值增加26.6%。图6 给出了钢格室承担的轴力比例的变化规律，随着与后承压板距离的增加，钢格室承担的轴力比例逐渐减小，在钢格室-混凝土过渡段截面处减小至0。从图中可以计算出后承压板通过填充混凝土承压作用承担的轴力比例。随着钢格室高度从1.2 m 减小至0.8 m，后承压板承担的轴力比例从75.3%减小至69.5%，表明钢格室高度减小33.3%，通过填充混凝土承压作用承担的轴力比例减小7.8%。

图5 钢格室顶板的纵向应力Fig.5 Longitudinal stress of the top plate of the steel cell

图6 钢格室承担的轴力比例Fig.6 The proportion of axial force borne by the steel cell

计算分析表明钢-混结合段通过后承压板的承压作用承担的轴力比例约占70%～75%，且钢格室高度的变化对于钢格室承担的轴力比例影响不大。钢-混结合段主要通过钢格室的外圈钢板将荷载从钢梁过渡段平顺地传递至混凝土梁过渡段。考虑到混合梁刚构桥的刚度过渡平稳性，钢-混接头处的刚度突变越小，对行车平顺性越有利。因此，在钢-混结合段承载的安全储备足够的前提下，可以对钢格室的高度进行优化。但是，钢格室的高度除了满足受力需求，还要保证施工的可行性(焊接钢结构和浇筑填充混凝土的操作空间)。结合变化格室高度的参数分析结果，提出如下钢-混结合段优化方案：将钢-混结合段顶、底部钢格室的高度从1.2 m 减小至0.8 m，将顶部钢格室的底板和底部钢格室的顶板的板厚从25 mm 减小至16 mm，将钢格室U 形开孔剪力板改为O 形开孔剪力板，以期改善钢格室对填充混凝土的面外约束效应。优化后的钢-混结合段局部构造如图7 所示。

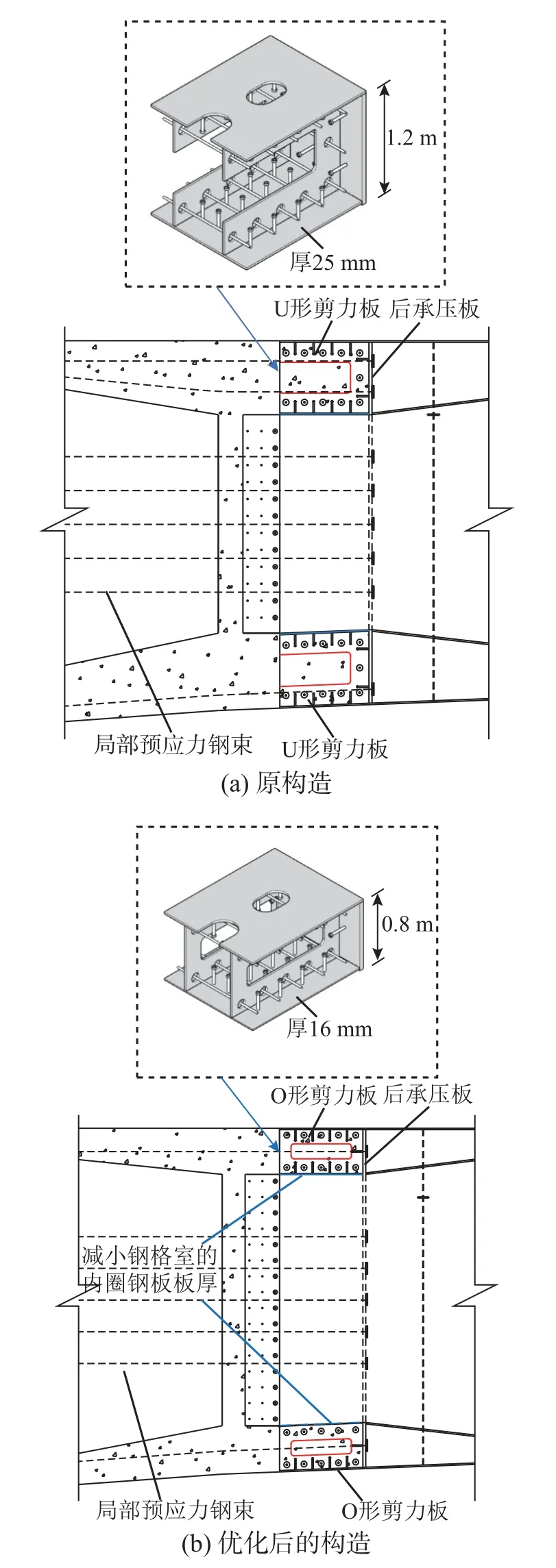
图7 钢-混结合段的构造优化Fig.7 Structural optimization of the steel-concrete composite segment

2 试验研究

为了研究混合梁刚构桥钢-混接头中构件的破坏先后顺序及失效模式，并验证优化后的钢-混结合段构造的安全性，取钢-混结合段中的标准格室作为原型(见图3)，设计缩尺模型开展静力试验。在工程设计中，钢-混接头通过配置局部预应力钢束，使得钢-混结合段全截面受压。因此，钢-混结合段极限承载力试验的加载方案采用轴向压力和剪力协同加载，验证局部格室的压剪承载力满足设计需求，并进一步研究轴向压力作用下钢-混结合段的破坏形态。

2.1 试件设计方案

试验设计方案如表1 所示。由于加载设备的空间限制，按1∶2 缩尺比设计钢-混接头的试验模型。试件SCC-1 以实桥构造为原型，试件长2.2 m，包括钢梁过渡段0.7 m、钢-混结合段0.75 m 和混凝土梁过渡段0.75 m。截面尺寸0.6 m×0.6 m，包含1 个标准钢格室和2 个对称的半钢格室。除承压板厚25 mm 外，钢格室和钢梁过渡段的板件厚度均为12 mm，焊钉规格为Φ13×100 mm。试件构造设计如图8 所示。

表1 试件设计方案Table 1 Design scheme of specimens

图8 试件构造设计 /mmFig.8 Structural design of specimens

试件SCC-2 以优化后的钢-混结合段构造为原型，将U 形开孔剪力板改成O 形开孔剪力板，同时将钢格室底板板厚从12 mm 减小为8 mm。为了保证钢梁过渡段不先于钢-混结合段破坏，特地将钢梁过渡段长度调整为0.4 m，并将板厚适当加厚，同时在钢梁过渡段上焊接贴板和板肋。

试件SCC-1 工况1 预计的破坏模式为钢梁过渡段破坏，所以当其破坏后，在钢结构加工厂内把破坏后的钢结构切割掉，重新焊接新的钢板并在钢梁过渡段上焊接贴板和板肋，对钢结构进行补强加固后，再次进行工况2 试验。

2.2 试件加载和测试方案

采用压剪机测试钢-混结合段试验模型在压剪耦合作用下的受力性能以及在轴向受压下的极限承载力和破坏形态。根据有限元模型计算结果并考虑试验相似比，试验模型的设计轴向压力为2150 kN，设计竖向剪力为250 kN。如图9 所示，轴向压力分别作用于钢梁过渡段和混凝土梁过渡段的截面形心，水平剪力作用于混凝土梁底座。

图9 加载方案Fig.9 Loading scheme

试件SCC-1(工况1)采用轴向受压加载方式，试验目的是为了验证钢-混结合段的轴压承载力大于钢梁过渡段的轴压承载力。为了测试试件SCC-1(工况2)和试件SCC-2 的压剪力学性能，采用同步施加轴向压力和水平剪力的加载方案且使用力加载控制。依据实桥受力情况，剪压比设置为1∶10，如图10 所示。为得到试件的受压破坏模式，需要避免其在水平方向上发生剪坏。因此，当水平剪力加至450 kN(1.8 倍设计剪力)后持荷，在这一荷载等级下观察试件的受力状态。随后，继续施加轴向压力且当试件接近破坏时，卸除水平剪力。

图10 试验加载制度Fig.10 Loading steps of experiment

试验测试内容包括钢-混结合段的轴向受压承载力、钢-混接头的轴向变形、局部预应力钢束的锚下压力、钢格室顶板应变和底板应变、填充混凝土和混凝土过渡段的应变。

3 试验结果

3.1 试验现象

试验结果汇总于表2 中。对于试件SCC-1(工况1)，当轴向压力加载至Pu=7100 kN 时，钢梁过渡段板件发生局部失稳，如图11 所示，试件达到受压极限破坏状态，而此时钢-混结合段仍处于弹性状态。如图12 所示，当轴向压力加载至0.32Pu时，钢梁过渡段腹板的内外侧测点的应变差值大于50 µε，这一差值表明钢腹板出现了面外应力，说明了钢梁过渡段腹板有鼓出的趋势。试验表明：实桥设计的钢梁过渡段的极限承载力小于钢-混结合段的极限承载力。

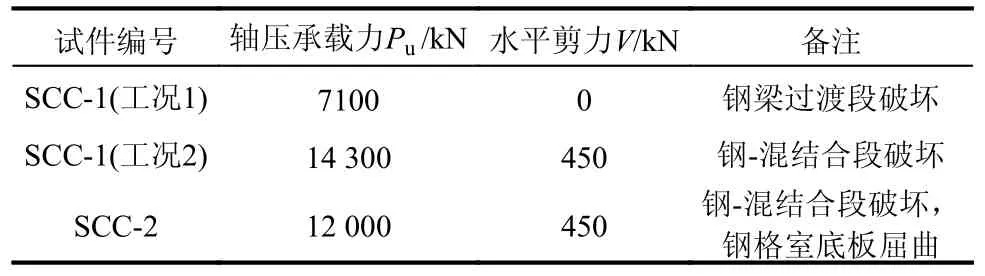
表2 试验结果汇总Table 2 Summary of test results

图11 试件SCC-1(工况1)钢梁过渡段板件局部失稳Fig.11 Local buckling of panels in the steel girder transition section of specimen SCC-1 (case 1)

图12 钢梁过渡段腹板测点的轴向压力-应变曲线Fig.12 Axial compression-strain curve of web plate measuring points of the steel girder transition section

由于试件SCC-1 的钢-混结合段在工况1 加载结束后仍然处于弹性状态，所以在试验设计时，对其钢梁过渡段进行更换并加固后，再进行工况2加载是可行的。对于试件SCC-1(工况2)，当轴向压力加载至4500 kN(2.1 倍设计轴向压力)，水平剪力加载至450 kN(1.8 倍设计竖向剪力)时，试件外观保持完好，受力处于线弹性状态。当轴向压力加载至14 300 kN 时，钢格室顶板与混凝土过渡段局部承压的位置(图13 中红色标记所示)出现压溃，表层混凝土剥落，纵向钢筋鼓出屈曲，钢-混结合段达到受压极限破坏状态，如图13 所示。试验结束后，凿除钢格室内压溃的填充混凝土，发现钢-混结合段的破坏模式为钢格室填充混凝土压溃，而焊钉和PBL 连接件均未被剪断，如图14 所示。

图13 试件SCC-1(工况1)钢-混结合段压溃Fig.13 Crushing failure in the steel-concrete composite segment of specimen SCC-1 (case 1)

图14 试件SCC-1(工况2)的焊钉连接件未被剪断Fig.14 Stud connectors of specimen SCC-1 (case 2) have not been snipped in failure

对于试件SCC-2，当轴向压力加载至4500 kN，水平剪力加载至450 kN，试件受力处于线弹性状态。当轴向压力加载至约12 000 kN 时，钢-混结合段压溃，表层混凝土剥落，钢格室底板出现以开孔剪力板为节线的局部受压屈曲，纵向钢筋鼓出屈曲，如图15～图16 所示。该试件的混凝土和钢结构基本同时达到了极限破坏状态。

图15 试件SCC-2 钢-混结合段压溃Fig.15 Crushing failure in the steel-concrete composite segment of specimen SCC-2

图16 试件SCC-2 钢格室底板受压屈曲Fig.16 Compression buckling failure in the bottom panel of steel cells of specimen SCC-2

分析试件SCC-1(工况2) 和SCC-2 的破坏现象发现，由于钢-混结合段的受压破坏模式是填充混凝土压溃，所以将钢格室的U 形开孔剪力板改成O 形开孔剪力板可以提高钢格室对填充混凝土的面外约束作用，如图17 所示。

图17 O 形剪力板对填充混凝土的面外约束作用Fig.17 Out-of-plane restraint effect on filled concrete of Oshaped perforated shear plates

3.2 试验测试数据

试件的轴向压力-变形曲线如图18 所示。从图中可以看出，在同一级荷载下，钢格室顶板侧的变形大于底板侧的变形，说明轴向压力通过顶板传递的比例大于底板传递的比例。当轴向压力小于0.70Pu(试件SCC-1 工况2)和0.67Pu(试件SCC-2)时，轴向压力-变形曲线近似呈直线，说明试件处于线弹性受力状态。随着轴向压力增大，试件开始进入塑性阶段。当加载至极限荷载时，试件SCC-1(工况2)和SCC-2 的顶板轴向变形分别约为8.7 mm 和5.6 mm。

图18 轴向压力-变形曲线Fig.18 Axial compression-deformation curve

试件的预应力钢束锚下压力(局部预应力钢束锚固在后承压板上)随轴向压力的变化规律如图19所示。随着轴向压力的增加，预应力钢束的预张力逐渐卸载，且卸载斜率逐渐变大，说明钢-混结合段在进入塑性阶段后，预应力钢束的锚下压力数值成为判断钢-混结合段达到极限破坏状态的重要指标。虽然试件的钢束预张力随轴向压力增大而逐渐卸载，但是当试件临近压溃时钢束仍保持较高的张力，试件SCC-1(工况2)和试件SCC-2 的剩余张力分别是初张力的89.4%和82.8%。对数据进行回归分析，锚下压力与轴向压力关系曲线的拟合方程呈三次函数分布。

图19 锚下压力-轴向压力曲线Fig.19 Anchor pressure-axial compression curve

钢格室顶、底板应变随距后承压板距离的变化规律如图20～图21 所示。从图中可以看出，随着与后承压板的距离逐渐增加，钢格室顶、底板的应变均逐渐减小，且顶板应变显著大于底板应变，说明钢格室顶板分担的轴力占比例较大。根据应变数据换算得原设计的钢-混结合段顶板分担的轴力约为底板的1.67 倍。

图20 试件SCC-1(工况2)钢格室顶、底板应变随距后承压板距离的变化规律Fig.20 Strain curves of top/bottom plate of steel cells with distance from rear bearing plate in specimen SCC-1 (case 2)

图21 试件SCC-2 钢格室顶、底板应变随距后承压板距离的变化规律Fig.21 Strain curves of top/bottom plate of steel cells with distance from rear bearing plate in specimen SCC-2

填充混凝土应变随距后承压板距离的变化规律如图22 所示。从图中看出，随着与后承压板距离的增加，混凝土应变逐渐增大，其规律性与钢格室应变的变化规律相反，说明钢-混结合段能够有效地将钢梁过渡段承担的轴力传递给混凝土梁过渡段。

图22 填充混凝土应变随距后承压板距离的变化规律Fig.22 Strain curves of filled concrete with distance from rear bearing plate

3.3 分析与讨论

试验测试了在轴向压力作用下钢格室和填充混凝土的应变规律，获得了钢-混结合段的破坏形态。结合试验结果分析钢-混结合段的传力机理，如图23 所示。钢梁过渡段通过钢-混结合段将轴向压力N传递至混凝土梁过渡段一共有5 条传力路径，分别是后承压板与填充混凝土的直接承压传力R1、PBL 连接件的剪切传力R2、焊钉连接件的剪切传力R3、钢格室顶板、底板和剪力板与填充混凝土之间的摩擦传力R4和钢格室顶板、底板和剪力板与混凝土梁过渡段之间的局部承压传力R5。由于焊钉和PBL 连接件被包裹在填充混凝土中，所以连接件的剪切传力也是直接作用于填充混凝土。

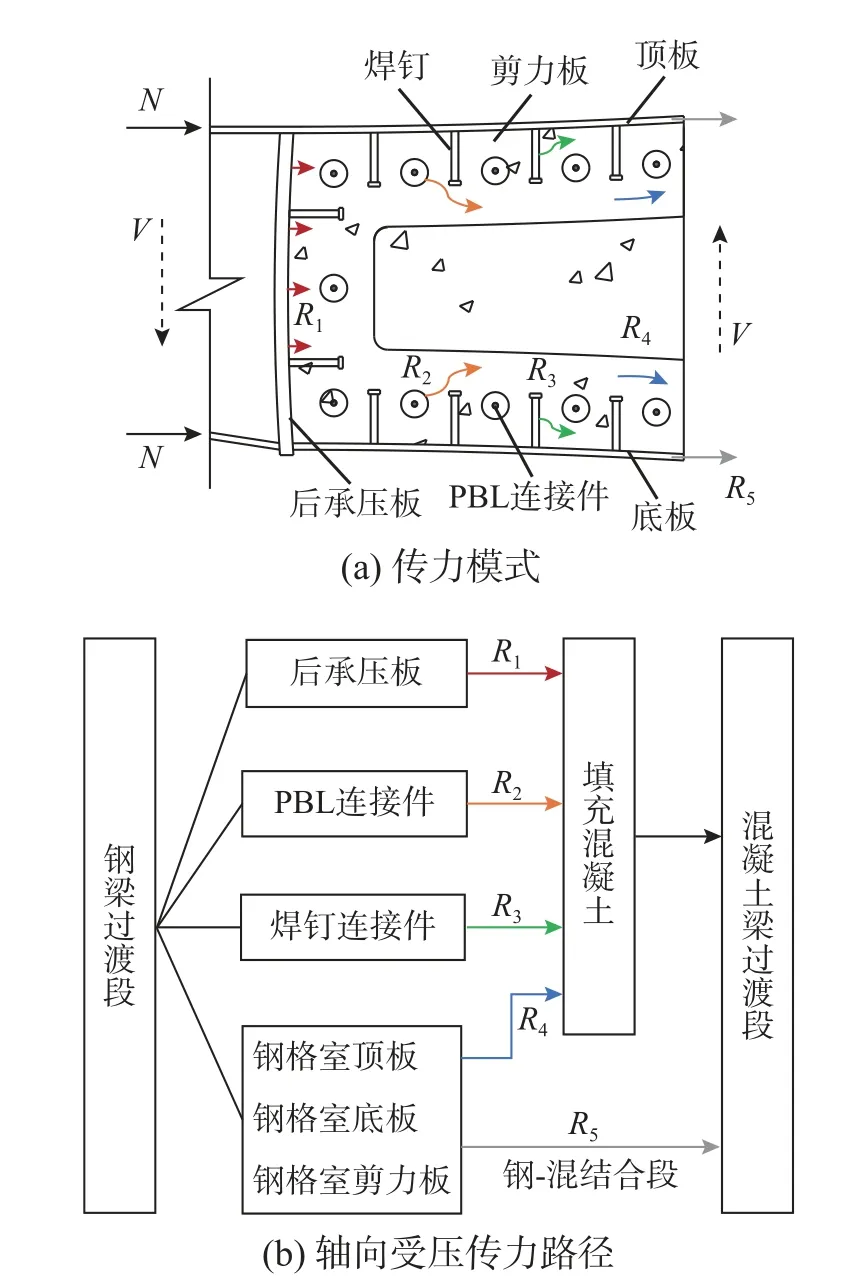
图23 钢-混结合段传力机理Fig.23 Force transmission mechanism of the steel-concrete composite segment

在后承压板与填充混凝土接触面位置处，通过承压作用传递的轴力R1所占比例较大，剩余轴力由钢格室Rs分担。参数分析表明，钢格室高度的变化对后承压板承担的轴力比例的影响不大。

在钢-混结合段初步设计时，可以按照以下简化方法计算后承压板位置处钢与混凝土的轴力分配：

式中：Nm、Na和Np分别为混合梁刚构桥钢-混接头处作用的弯矩(表示成一对力偶，符号以受压为正)、轴力(由混凝土梁的预应力钢束产生)和承压板处锚固的局部预应力钢束产生的轴力分量；α为承压板的轴力承担比例，根据有限元试算结果，α数值可以取为0.7～0.75。在得到钢格室和混凝土各自承担的轴力后，可以对结合段的各部分构件进行初步设计。

试验结果表明：实桥钢-混接头的极限破坏状态由钢梁过渡段控制，钢梁过渡段的屈曲承载力约为设计轴向压力的3.30 倍，且约为钢-混结合段极限承载力的50%。在正常使用阶段的荷载作用下，混合梁连续刚构桥的钢-混接头处于线弹性受力状态。在承载能力极限状态下，实桥钢-混结合段的轴压承载力约为设计轴向压力的6.65 倍，说明钢-混结合段构造设计得偏于保守，结合段有较大的优化空间。

本文优化后的钢-混结合段的钢格室高度降低1/3，局部钢板厚度减小1/3，其轴压承载力约为设计轴向压力的5.58 倍。与优化前相比，钢-混结合段轴压承载力降低16.1%，但是仍然大于原设计的钢梁过渡段的失稳承载力，说明将钢格室高度降低后，钢-混结合段的受力仍然能够满足设计需求。此外，把结合段的U 形开孔剪力板改为O 形开孔剪力板，可增强钢格室顶、底板对填充混凝土的面外约束效应，有助于提高钢-混结合段的极限承载力。

有限元分析和试验结果也表明钢格室通过顶板传递轴向压力的比例大于通过底板传递的比例。因此，在设计时可以减小顶部钢格室的底板和底部钢格室的顶板的板厚。由于钢-混结合段内的填充混凝土需要由钢格室的顶板浇筑孔向内浇筑，不便于填充混凝土的浇筑和振捣，所以为了施工方便，在设计时可以考虑取消钢-混结合段底部钢格室的顶板，这样便于将填充混凝土浇筑密实，但是需要通过计算复核和试验验证确保该构造满足承载力设计需求。

4 结论

针对混合梁刚构桥，本文对钢-混结合段的局部模型进行变化钢格室高度的参数分析和静力破环性试验研究，得到如下结论：

(1) 钢格室高度的变化对钢-混结合段后承压板承担的轴力比例的影响不大，后承压板的承压作用承担的轴力比例约占70%～75%，可为钢-混结合段初步设计提供参考；

(2) 现有设计的钢-混接头的失效模式为钢梁过渡段先于钢-混结合段破坏，破坏模式为钢梁过渡段板件发生局部受压屈曲，钢梁过渡段和钢-混结合段的承载力安全储备系数分别为3.30 和6.65，说明结合段有较大的优化空间；

(3) 本文提出的钢-混结合段优化构造，将钢格室高度降低1/3，局部钢板厚度减小1/3。试验得到钢-混结合段的轴压承载力仍高于钢梁过渡段的屈曲承载力，且安全储备系数为5.58；

(4) 将钢格室内的U 形开孔剪力板改为O 形开孔剪力板，可增强钢格室顶、底板对填充混凝土的面外约束效应，有助于提高钢-混结合段的极限承载力；

(5) 由于钢-混结合段轴向压力主要通过钢格室的外圈钢板传递，所以减小顶部钢格室的底板和底部钢格室的顶板的板厚是可行的。