给定预算下基于相对熵置信区间的蒙特卡洛树搜索最优动作识别算法

刘郭庆 钱宇华 张亚宇 王婕婷

（山西大学大数据科学与产业研究院 太原 030006）

（计算智能与中文信息处理教育部重点实验室（山西大学）太原 030006）

（山西大学计算机与信息技术学院 太原 030006）（guoqingl1001@163.com）

现有多数人工智能算法是通过自上而下的人为设计在有限的环境中实现特定机制或解决特定问题，不能很好地适应任务交叉复杂、场景未知多变的现实环境.针对这一困境，以“最大化奖励，自适应学习”为原则的强化学习被视为一个有效途径.强化学习[1-2]通过与环境交互得到反馈进行优化，无需提前标注数据和探索数据结构，因此能够更加适应任务和需求多变的开放人工智能场景，被视为开放环境下最具前景的方法之一.然而现有的强化学习算法仍然面临许多挑战：1）泛化性不足，即强化学习算法对环境变化的健壮性和在部署过程中的适应性仍需加强；2）可解释性不足，即对模型设计者和使用者而言，模型所学知识、模型内部逻辑等关键信息尚不明晰；3）指导性不足，即对任务场景的影响因素和的内在机理的研究较浅.为了应对这3个挑战，亟需从理论角度对强化学习领域中的重要算法以及模型进行分析.

自Kocsis 和Szepesv´ari以及Coulom[3-4]提出蒙特卡洛树搜索（Monte Carlo tree search , MCTS）后，MCTS作为一种典型的强化学习模型，其在树结构表示的组合空间中通过启发式搜索进行连续决策.后续工作通过引入领域知识或结合其他技术对特定问题进行处理，已经在化学合成[5]、组合优化[6]、规划调度[7-8]和机器翻译[9]等领域得到了成功的应用.其中最为瞩目的进展是AlphaGo[10]首次击败了人类围棋冠军和其他围棋程序，被认为是人工智能的里程碑式突破.随后Alpha Zero[11]从白板状态起步，实现了在国际象棋、围棋和将棋3个领域超越人类专家和其他程序的水平，MuZero[12]在多个不相关任务上实现超越人类的水平，为创造通用人工智能甚至理解智能本身提供了可能性.

MCTS基于树结构构建问题模型，其中节点表示状态，边表示从一个状态到另一个状态的动作.其面临的主要问题是在当前状态下，玩家如何在众多可行动作中选择出最优动作以确保获胜.MCTS主要包含4个流程：选择（从根节点开始，根据给定的搜索策略递归地选择子节点，直至叶子节点停止）、扩展（对非终止节点的叶子节点创建一个或者更多的子节点）、模拟（对扩展的子节点通过蒙特卡洛方法进行模拟得到估计值，直至终止节点停止）和回溯（根据模拟结果更新扩展节点到根节点这一路径上的节点估值）.重复进行这4个流程，当算法停止后选择当前状态下价值最高的边对应的状态作为输出.然而在现实场景中，基于实际任务构建的树结构往往具有巨大的搜索空间，但由于计算资源匮乏或者计算成本高等原因，完全充分地对树结构进行搜索是难以实现的，因此在有限的预算下高效合理地分配计算资源从而获得当前状态下的最优动作是目前研究的一个重要思路.

由于2名玩家、完全信息、零和博弈是MCTS模型体系中一个基础且重要的场景，因此，本文基于该场景对上述问题进行分析，在第2节中提出了抽象模型——极小极大采样树（minimax sampling tree, MST）模型并对树模型中的相关概念定义了数学表示，给出了固定预算下最优动作识别问题的算法目标.在第3节中，构造了包含叶子节点胜率估计、第1层节点值估计、最优节点选择3个部分的MST最优动作识别算法DLU （relative entropy confidence interval based pure exploration）.该算法首先基于相对熵构建了节点估值区间，以对叶子节点胜率进行更加准确地评估，进而从根本上提升算法的准确性；然后进行估值区间上传；最后给出了最优节点选择策略.在第4节中，基于DLU算法推导了输出动作的误差上界，从理论角度给出了算法误差的相关影响因素.在第5节中，在人造树模型和井字棋2种场景下对算法性能进行验证分析.实验结果表明，在固定预算设定下，所提出的基于相对熵置信区间的最优动作识别算法类在低预算时具有更好的性能表现，且模型越复杂识别难度越高时，该算法类的性能优势越显著.同时，在井字棋博弈场景下，将DLU算法与已知具有理论保证的最优算法进行比较，可以看出DLU算法能有效识别最优动作.同时，DLU算法具有快速选择采样节点的策略，从而降低时间消耗.

1 相关工作

高效的MCTS选择策略的目的是在探索（未经过充分测试的行动）和利用（迄今为止确定的最佳行动）之间保持适当的平衡，已有很多学者对其进行了全面深入地研究，相关进展在文献[13-14]中进行了详细的分类和阐述.经典的MCTS策略包括基于树结构上的上置信界（upper confidence bound applied to tree，UCT）算法[3,15]和汤姆森抽样算法[16]等，它们通过非对称的方式搜索博弈树，使得有希望的走子路径被更彻底地搜索以提高效率.然而具体的任务场景往往包含巨大的搜索空间和复杂的算法模型，基础的或单一的树搜索算法无法有效识别出最优动作，旨在解决这一问题的策略包括：限制可用行动的数量[17]、提前结束模拟阶段[18]、构造信息集合[19]、结合领域知识[20]、建模对手行为[21]等.同时，将MCTS与进化学习[22-23]、联邦学习[24]、迁移学习[25]等方法相结合实现优势互补，进而增强收敛性、泛化性、迁移性和可解释性等性能.虽然这些策略极大地提高了算法的效率和性能，但其中大部分策略仅通过实验对比展现优势，缺少理论保证和影响因素分析，导致算法缺少说服力.

将多臂赌博机（multi-armed bandit，MAB）算法引入到MCTS是促使其理论研究发展的关键一步，多臂赌博机的理论研究可为MCTS的分析提供有效参考.多臂赌博机[26]最初被提出用于管理临床试验，现在被常规应用于计算广告、电子商务等广泛任务中.多臂赌博机包含遗憾最小化[27]和最优摇臂识别 （best arm identification，BAI）[28]2个主要分支.文献[29]通过引入KL散度得到摇臂的置信上界，从算法和理论2方面对遗憾最小化问题进行分析.最优摇臂识别算法要么在给定的置信度阈值下追求最少的试验次数，要么在给定的试验次数下追求识别最优摇臂的最小误差[30-31]，固定预算下的MCTS最优动作识别问题与后者非常相似.

与BAI问题类似，MCTS最优动作识别问题的理论研究也可分为固定置信度和固定预算值2种设定.对于固定置信度的设定，文献[32]将BAI方法引入到MCTS中，通过自底向上的方式对树进行操作，并给出了返回具有可接受误差的节点所需的采样次数上界.文献[33]提供了另外2种MCTS算法并得到了严格的概率近似正确分析和包含多个相关因素的样本复杂度的高概率上界.对于固定预算的设定，文献[34]假设随机累计奖励服从期望已知、均值未知的高斯分布，通过将排序选择算法引入MCTS中提出了OCBA-MCTS算法，并得到了节点正确选择的下界保证.然而，在奖励样本较少或整体方差较大时，文献[33]给出的状态动作值的后验分布假设不能完全保证，造成理论保证不足.同时，OCBA-MCTS算法的正确选择概率下界表明方差、间隔等相关因素与算法性能相关，其他相关因素仍需进一步探索.

2 极小极大采样树模型

本文对2名玩家、完全信息、零和博弈的蒙特卡洛树搜索模型进行分析，为了有效地进行理论研究，引入了MCTS的抽象模型——MST模型，如图1所示.该模型的大小由深度Depth和宽度Edge定义，即每个状态下有Edge 个可行动作，树结构有Depth个状态层，最上层被定义为根节点层，最底层被定义为叶子节点层.根节点s0所在层数被定义为D(s0)=0，叶子节点f所在层数被定义为D(f)=Depth，叶子节点集合被定义为F.为了在树状结构中反映博弈过程，将玩家所在的偶数层节点定义为MAX节点，将对手所在的奇数层节点定义为MIN节点.

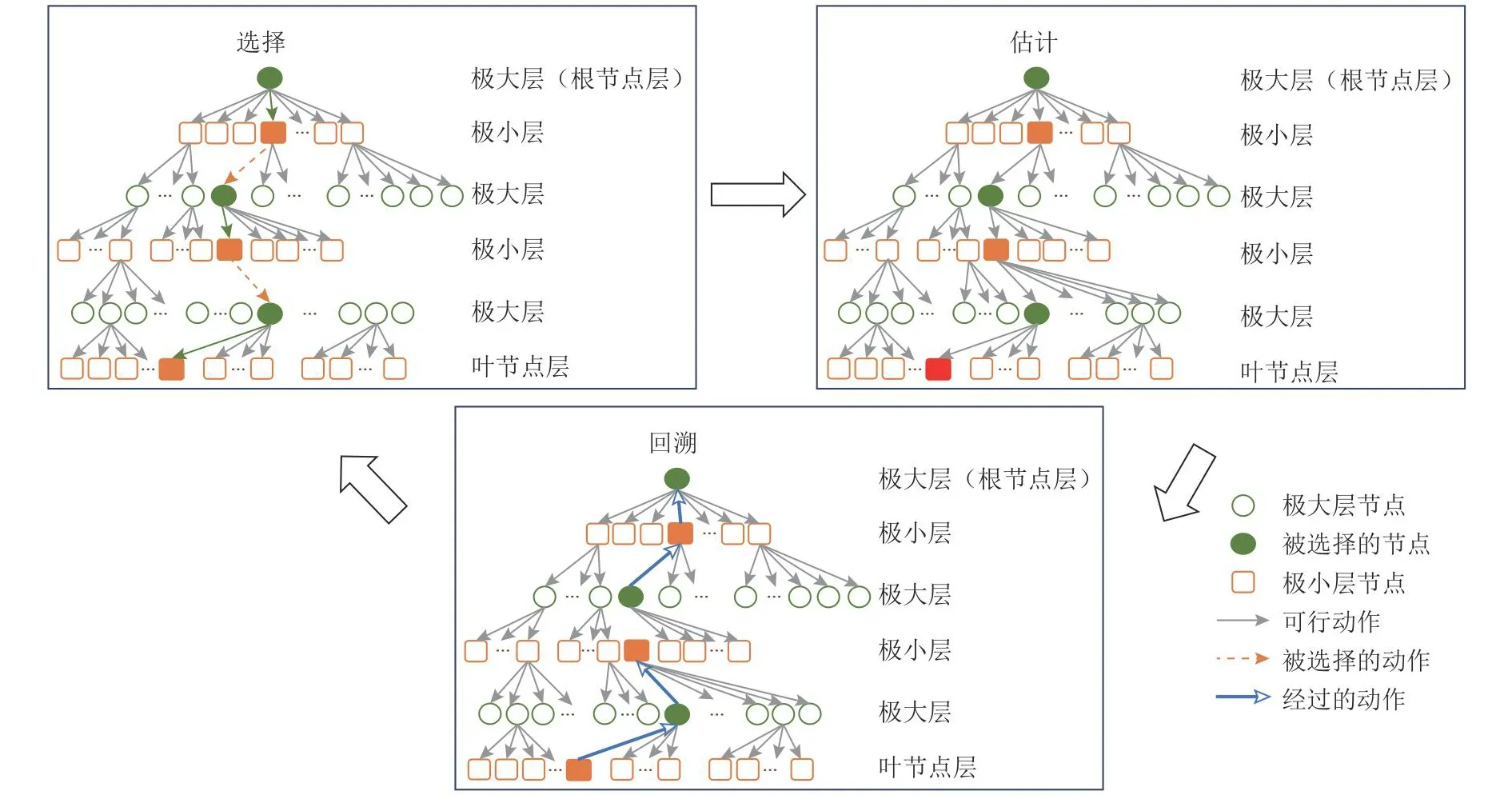
Fig.1 Flow chart of MST model图1 极小极大采样树模型流程图

MST模型包含3个流程：选择、估计和回溯.在选择流程中，MST通过给定策略选择当前状态下的最优动作并不断下行，这与MCTS中的选择流程一致.但MST将MCTS模型中的扩展流程和模拟流程合并为一个估计流程，即将扩展和模拟流程中通过随机走子形成的子树由一个服从伯努利分布的叶子节点f替代，其期望值pf为玩家在当前状态的真实胜率.在实际探索过程中，叶子节点的期望值pf对玩家而言是未知的，因此玩家需要通过对叶子节点f的真实胜率进行估计.在回溯流程中将叶子节点估计值进行上传，对该叶子节点的所有祖先节点的估值进行更新.由于MST依据叶子节点估值对所有非根节点进行估值，因此找到高效准确的叶子节点估值方法是最基础和关键的一步.本文定义C(s)和P(s)分别表示节点s的子节点集合和1个父节点，从而可以得到树结构中所有节点的期望值Vs： 如果节点s是叶子节点f，则Vf=pf；否则：

MST中的最优动作识别即识别出根节点s0下具有最大期望值的第1层节点：

在固定预算设定中，最优动作识别算法迭代N次后可返回第1层节点，算法旨在最小化识别误差.

3 基于相对熵置信区间的最优动作识别算法

面向第2节中的MST模型，本节结合固定预算设定构造了MST最优动作识别算法DLU，其包含3个部分：叶子节点胜率估计、第1层节点值估计、最优节点选择，其分别对应MST中估值、回溯和选择3个流程，3个部分自下而上循环执行.首先在3.1节中，本文提出了基于相对熵的置信区间方法以估计叶子节点胜率.其次在3.2节中给出了区间上传策略，依照该策略可以得到树结构中所有非根节点的置信区间，从而对树节点期望值进行估计.最后在3.3节中，本文给出了一种基于节点上下置信界的最优节点选择策略，其包含选择采样节点和输出推荐节点2部分.

3.1 叶子节点胜率估计

在DLU算法中，从第1节点中选择出的最优节点是基于节点的估计值进行的，而第1层节点的估计值是通过以一定方式上传叶子节点的估计值而得到，因此叶子节点估值的准确性对最优节点选择是否正确和是否高效具有根本性的影响，更加准确的叶子节点估计策略将显著提升算法性能.

为了对叶子节点f∈F的真实胜率V(f)=pf进行有效地估计，本文对叶子节点构造置信区间[35-36]：If(t)=[Lf(t),Uf(t)]，其中Uf(t)和Lf(t)分别是第t轮叶子节点胜率的置信上界和置信下界.在MST中设定叶子节点f∈F服从期望值为pf的伯努利分布β(pf)，通过对其进行采样估值来表示MCTS中扩展阶段和模拟阶段形成的随机走子过程.具体而言，在第t轮，算法选择叶子节点ft并对其进行采样得到样本Xft～βft，进而计算叶子节点平均值并按照定义1得到置信区间Ift(t).

定义1.当算法第t次进行选择流程并选择叶子节点ft时，可基于相对熵得到其置信区间Ift(t)：

其中置信上界和置信下界分别为：

在式（5）中，Nft(t)表示叶子节点ft直至第t轮时被选择的次数，pˆft(t)表示第t轮时叶子节点ft的平均值，α(Nft(t),λ)表示给定的探索函数，d(µ,µ′)为2个伯努利分布β和β′之间的相对熵，其中µ=E(β) 和µ′=E(β′)，即：

按照惯例，本文设定 0log0=0log0/0=0，及当x＞0时xlog(x/0)=+∞.对于任意的pˆf(t)∈[0,1], 函数y-→d((t),y)在区间 [pˆf(t),1]中是严格凸且单增.

3.2 第1层节点值估计

在得到叶子节点置信区间的基础上，需要将其进行上传以完成MST中的回溯流程.具体而言，由于MST由极小层和极大层交替组成，每次叶子节点ft的置信区间Ift(t)被更新后，依据式（6）将叶子节点的置信区间上传[33]：

上传过程直至第1层节点结束，从而完成ft每个祖先节点as∈AS的置信区间Ias(t)的更新，最终完成回溯流程.祖先节点集合AS定义为从根节点到达叶子节点ft时所有经过的节点.回溯流程完成后可以得到每个非根节点s包 含期望值V(s)的置信区间：Is(t)=[Ls(t),Us(t)].

在第t轮回溯流程中，第1层节点c∈C(s0)的置信区间Ic(t)为其期望值V(c)的估计范围，能够较为准确地表示当前状态下玩家的胜率，更紧的置信区间能更好地为最优第1层节点选择提供依据.

3.3 最优节点选择

根据第t轮第1层节点c∈C(s0)的期望值估值区间Ic(t)，本文基于多臂赌博机方法给出了一种基于上下置信界（lower and upper confidence bounds, LUCB）[37]的最优节点选择策略，其包含选择采样节点和输出推荐节点2个部分，当t≤N时每次选择一个第1层节点的代表叶子节点进行采样，当t＞N时输出推荐节点，该策略详细流程为：

1）选择采样节点部分被划分为确定备选节点和寻找代表叶子节点2个步骤.

①给出了以最高下界为准则的基于间隔的一致探索（unified gap-based exploration, UgapE）策略[38]，该策略基于置信界选择备选节点，更紧的置信界能够更加准确地刻画节点值，从而在低采样次数下更具优势.UgapE策略对于每个第1层节点c∈C(s0)，计算指标并确定2个备选节点分别为：

②选择lt和ut中具有较大置信区间的第1层节点置信区间越大表明该节点的不确定性更大，更需要探索.本文进一步定义第t轮每一个非叶节点s的 代表性子节点cs(t)为：

不断向下寻找代表性子节点，最终可获得第t轮每一个非根节点s的 代表性叶子节点rfs(t)为：

按照式（8）中的节点下传方式，选择Rt的代表叶子节点.

2）输出推荐节点部分即当算法满足N次采样后算法终止并输出推荐节点sˆN.DLU算法架构如算法1所示.

算法1.DLU算法.

输入：博弈树结构T， 探索函数α(n,λ)，预算值N；

① fort=1,2,…,|F|

② 对每个叶子节点f∈F进行一次采样，更新每个叶子节点的采样次数Nf(t)并按照式（5）计算置信区间；

③ 按照式（6）更新每个非叶非根节点的置信区间Is(t)；

④ end for

⑤ fort≤N

⑥ 按照式（7）确定2个备选节点lt,ut；

⑦ 选择具有较大置信区间的节点：

⑧ 选择Rt的代表叶子节点rft；

⑨ 计算代表叶子节点rft的平均值pˆrft(t)并更新置信区间Irft(t)；

⑩ 更新叶子节点的每个祖先节点as∈AS的置信区间Ias(t)；

⑪t=t+1；

⑫ end for

4 误差上界分析

第3节提出了DLU算法，该算法旨在给定预算时最小化识别误差本节对最优动作的识别误差上界进行推导.

首先，当设定d(µ,µ′)为2个期望值µ=E(β)和µ′=E(β′)的伯努利分布β和β′之间的相对熵时，基于Pinsker不等式可知这表明基于相对熵构造的叶子节点置信区间If(t)比基于霍夫丁不等式构造的置信区间IHf(t)=[LHf(t),UHf(t)]更紧，即If(t)⊆IHf(t)，其中：

进而可知当使用相对熵构造置信区间时，定理1成立.为了更清晰地进行证明，本文先给出了引理1.

引理1（引理5[33]）.令∈F If(t))成立，UGapE-MCTS算法使用探索函数：α(n,λ)=log(λ|F|)+3loglog(λ|F|)+1.5log(1+logn),λ≥1/max(0.1|F|,1)，

运行且在第t轮还未结束时，在第t+1轮选择叶子节点f后可得：

其中Hf为叶子节点f的复杂度项，其中表示第1层节点中最优动作与次优动作之间期望值之差的平方，表示f的祖先节点s与其父节点P(s)之间的期望值之差的平方.基于其可以得到在第t轮叶子节点f的采样次数Nf(t)与探索函数α（Nf(t),λ)的关系，H为所有叶子节点的复杂度项之和.

定理1.当DLU算法的采样次数设定为N＞8H(W+2log(1+log(8HW)))，可以得到算法识别最优动作的误差上界为：

其中，W=log(λ|F|)+3loglog(λ|F|).

证明：

文献[33]中在固定置信度的设定下，UGapEMCTS算法运行直至满足终止条件Uut(t)-Llt(t)＜η后停止采样并且得到终止次数τ.对于DLU算法，本文假设η=0且在探索函数α(n;λ)=log(λ|F|)+3loglog(λ|F|)+1.5log(1+logn)，λ≥1/max(0.1|F|,1)下运行UGapEMCTS算法N次后，返回节点，进而分为2种情况进行分析：

1）对P(V(s0)≠V(sˆN)|τ≤N)P(τ≤N)的上界进行分析.如果τ≤N，那么DLU算法在第τ轮满足了终止条件Uuτ(τ)-Llτ(τ)＜η，并且输出节点{1,2,…,N}也满足了该条件.同时当假设和成立时，由式（6）进行置信区间上传可得进而根据文献[33]中引理2可知到V(s0)=V().因此，如果V(s0)≠V(sˆN)，这意味着存在t∈[1,N]，εt不成立.即：

2）对P(τ＞N)进行上界分析，其表明算法在N次采样后还未停止的概率.如果τ＞N，那么DLU算法的输出节点其是在t∈{1,2,…,N}中具有最小指标Blt(t)的第1层节点.然后结合引理1可得：

其中可由引理1得到不等式（11）成立，是将UGapEMCTS算法在探索函数α(n;λ)中运行得到的.

基于引理1并结合DLU算法最终可得到结论：通过定理1可以得到，最优动作的识别误差与探索函数和叶子集合的复杂度项有关，这表明固定预算下的DLU算法可通过改进这些影响因素以提升算法性能.

5 实验分析

面向固定预算下的MCTS最优动作识别问题，为了最小化识别误差，本文基于相对熵构造节点置信区间以评估节点值.为了验证基于相对熵置信区间的算法优势，本节在2种实验场景下进行算法对比：人为构造的树模型和真实博弈场景井字棋.在每一种实验场景下，本文首先阐明了相关对比算法，然后给出了实验参数设置，最后进行实验分析.分析结果表明在人为构造的树模型下，本文所提出的基于相对熵置信区间的算法类在低采样次数下能显著地提高识别准确度，从而节省计算资源.在井字棋场景下，本文提出的DLU算法可以有效地识别最优动作,减少时间复杂度.

5.1 构造树模型场景

5.1.1 对比算法

首先，为了能够证明基于相对熵置信区间的算法能够从根本上提升算法性能，本文引入另一类备选节点计算策略：以最大均值为准则的EME策略[39]，该策略确定2个有希望的备选节点lt,ut的步骤为：

其次，本文在最优节点选择部分中提出了均匀采样（uniform sampling, RS）策略作为基准策略.与第3节使用的最优节点选择策略LUCB每次只对1个节点进行采样对比，均匀采样策略是每轮对所有第1层节点进行采样，详细的算法流程为：

算法2.RS策略算法.

输入：博弈树结构T，探索函数α(n,λ)，预算值N；

输出：第1层节点sˆ=lN.

① fort=1,2,...,|F|

② 对每个叶子节点f∈F进行一次采样，更新每个叶子节点的采样次数Nf(t)并计算置信区间If(t)；

③ 更新每个非叶非根节点的置信区间Is(t)；

④ end for

⑤ fort≤N

⑥ forc∈C(s0)

⑦ 选择第1层节点c的代表叶子节点；

⑧ 计算代表叶子节点rfc的平均值(t)并更新置信区间Irfc(t)；

⑨ 更新代表叶子节点rfc的祖先节点as∈AS(rfc)的置信区间Ias(t)；

⑩t=t+1；

⑪ end for

⑫ end for

然后，本文引入文献[33]中基于霍夫丁置信区间的2个算法，为了方便对比，将2个算法分别重命名为HLU算法和HLE算法.由于这2个算法只限定于LUCB策略，本文将这2个算法拓展至均匀采样策略下，形成了HRU算法和HRE算法使用的探索函数为：

最后，本文将第4节DLU算法中的UgapE策略替换为EME策略，提出了DLE算法，同时将DLU算法和DLE算法中的LUCB策略替换为RS策略分别生成了DRU算法和DRE算法.8个算法的对应关系如表1所示.

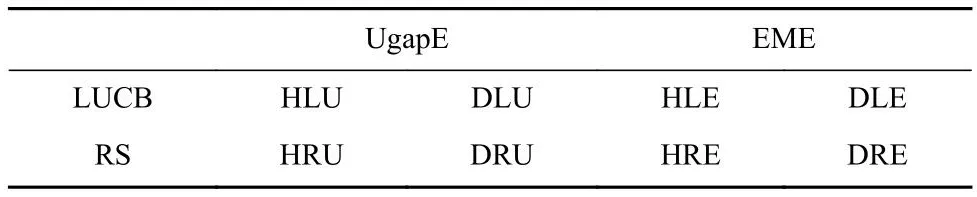
Table 1 Setting of Experimental Algorithms表1 实验算法设置

Table 2 Setting of Experimental Models表2 实验模型设置

5.1.2 实验模型

本文首先构造了3种树类别、15种树结构以验证算法的性能表现.由于边数Edge（表2中以E表示）和深度Depth（表2中以De表示，不包括根节点）是构成树结构的2个元素，本文在其基础上构造了边数变化、深度变化、固定积数的3种树类别.具体而言，对于边数变化的树类别，本文设定树的深度为2，构造边数分别为4，8，12，16，20的5种树结构.对于深度变化的树类别，本文设定树的边数为2，构造深度分别为2，4，6，8，10的5种树结构.同时，固定边数与深度之积S为24，得到(E,De)分别为（3，8），（4，6），（6，4），（8，3），（12，2）的5种树结构.

在每一种树结构下，进一步设置不同的节点间隔s_gap从而验证算法在节点区分难度不同的树模型的性能.节点间隔为2个同父结点取值的最小差值，设置取值为0.010或0.02，即

其中，V(s)表示节点s的 期望值，Ps表示节点s的父节点.

对于每一种树模型，基于叶子节点和树节点的个数给出不同倍数的采样次数，具体的比例见实验结果.设置参数λ=10.在每一种树结构下对应生成2000个模型以进行树搜索，最终对2000个模型上正确输出最优动作的次数取平均值作为该结构在对应采样倍数下的准确度：由于每个树模型中叶节点的期望值p∈（0，1），因此在实验过程中设定节点期望值的最大置信上界是1，最小置信下界是0.每个叶子节点的期望值在值空间中随机选择以保证模型的随机性，设定多种架构和类别能够更加全面地展现算法的性能优势，凸显算法对性能的影响.

5.1.3 实验结果

图2～7分别为3种树类别中不同节点间隔s_gap和采样倍数下的算法准确度，由于节点识别难度随着节点间隔的减小而增加，因此在小节点间隔时给定更高的采样倍数.8种算法在3种树类别上性能表现都具有相同结论，即采用准确度作为评价标准时，基于相对熵置信区间的算法类都优于基于霍夫丁置信区间的算法类.

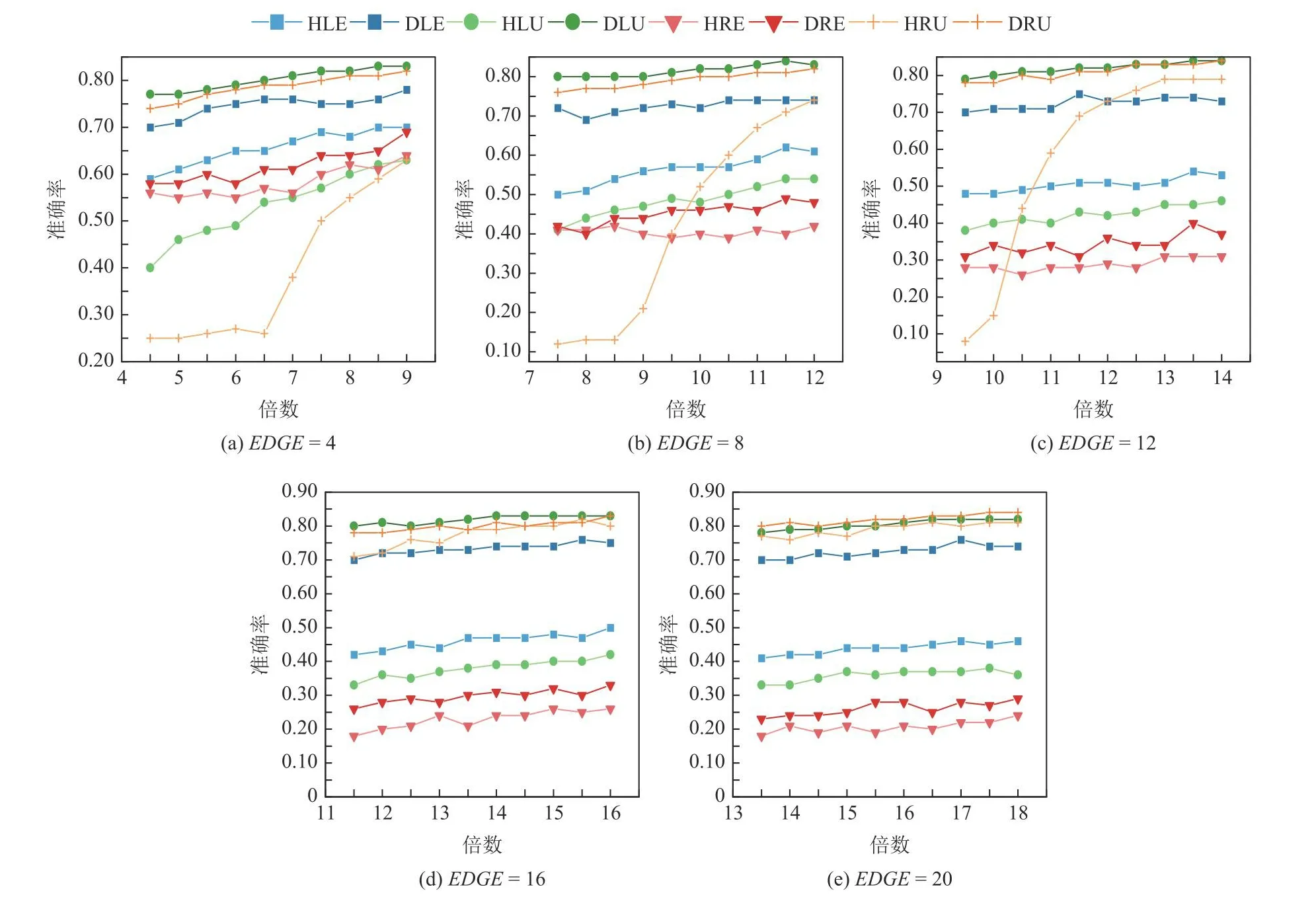
Fig.2 Accuracy of algorithms for edge-varing trees with node gap equals to 0.01图2 节点间隔为0.01时边数变化的树类别的算法准确度

表3表示边数变化的树类别下的5种树架构，可以发现随着边数的增加，总节点个数基本翻倍增加，因此给定的采样倍数也逐步增加.图2和图3分别表示边数变化的树类别在节点间隔分别取0.01和0.02时8种算法的准确度，可以发现除了DRE算法和HRE算法，其他基于相对熵置信区间的算法都显著优于对应的基于霍夫丁置信区间的算法.DRE算法和HRE算法准确度差距不显著可能是因为当边数增加时，第1层节点的取值逐渐接近，区分难度变大，需要更高的采样倍数才能区分性能差异.同时由于均匀采样策略对所有第1层节点使用相同的采样次数，没有在探索和利用之间进行均衡.然而，由于基于相对熵能构造更紧的置信区间从而更准确地对节点取值进行估计，因此DRE算法的准确度仍然高于HRE算法.同时HRU算法对采样倍数变化非常敏感，在低采样倍数下DRU算法具有明显优势，随着采样次数增加，HRU算法准确度有了极大的提升.

Table 3 Five Edge-varing Tree Structures表3 边数变化的5种树结构

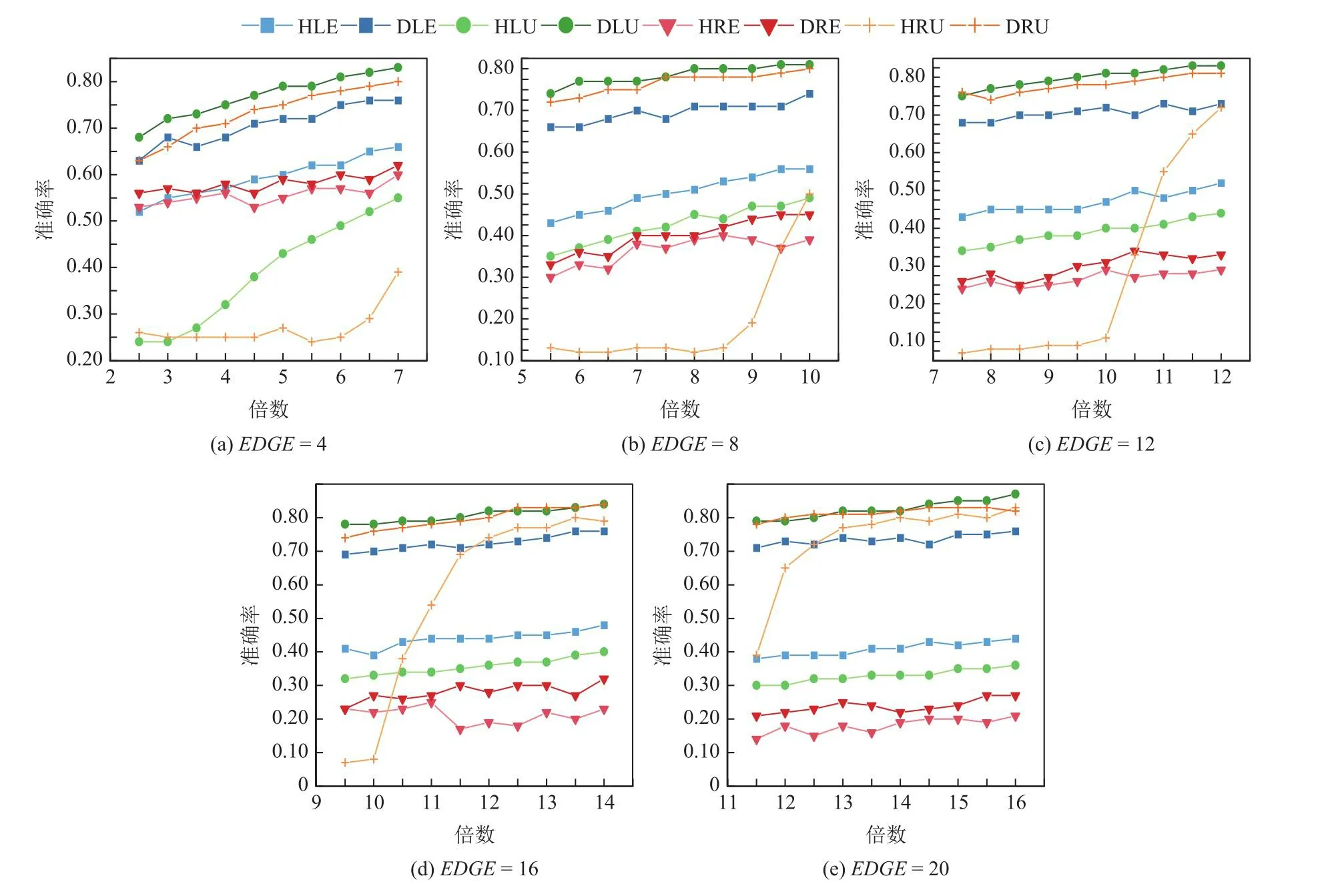
Fig.3 Accuracy of algorithms for edge-varing trees with node gap equals to 0.02图3 节点间隔为0.02时边数变化的树类别的算法准确度

表4为深度变化的树类别下的5种树结构，可以发现随着深度的增加，叶子节点个数和总节点个数急剧增长，因此在深度较小的树结构中增大采样倍数，在深度较大时减小采样倍数，从而将采样次数保持在合理范围内，以体现算法性能差距.图4和图5分别表示深度变化的树类别在节点间隔分别取0.01和 0.02时8种算法的准确度，可以发现基于相对熵置信区间的算法类相较于基于霍夫丁置信区间的算法类具有断层优势，且随着树结构深度增加，优势愈加明显.这是因为深度增加时，置信区间上传次数增加，更紧的置信区间能够更加精准地对节点取值进行估计，减少上传误差.

Table 4 Five Depth-varing Tree Structures表4 深度变化的五种树结构

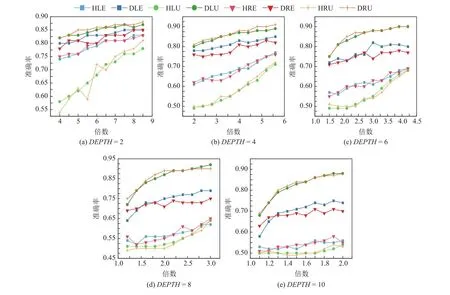
Fig.4 Accuracy of algorithms for depth-varing trees with node gap equals to 0.01图4 节点间隔为0.01时深度变化的树类别的算法准确度

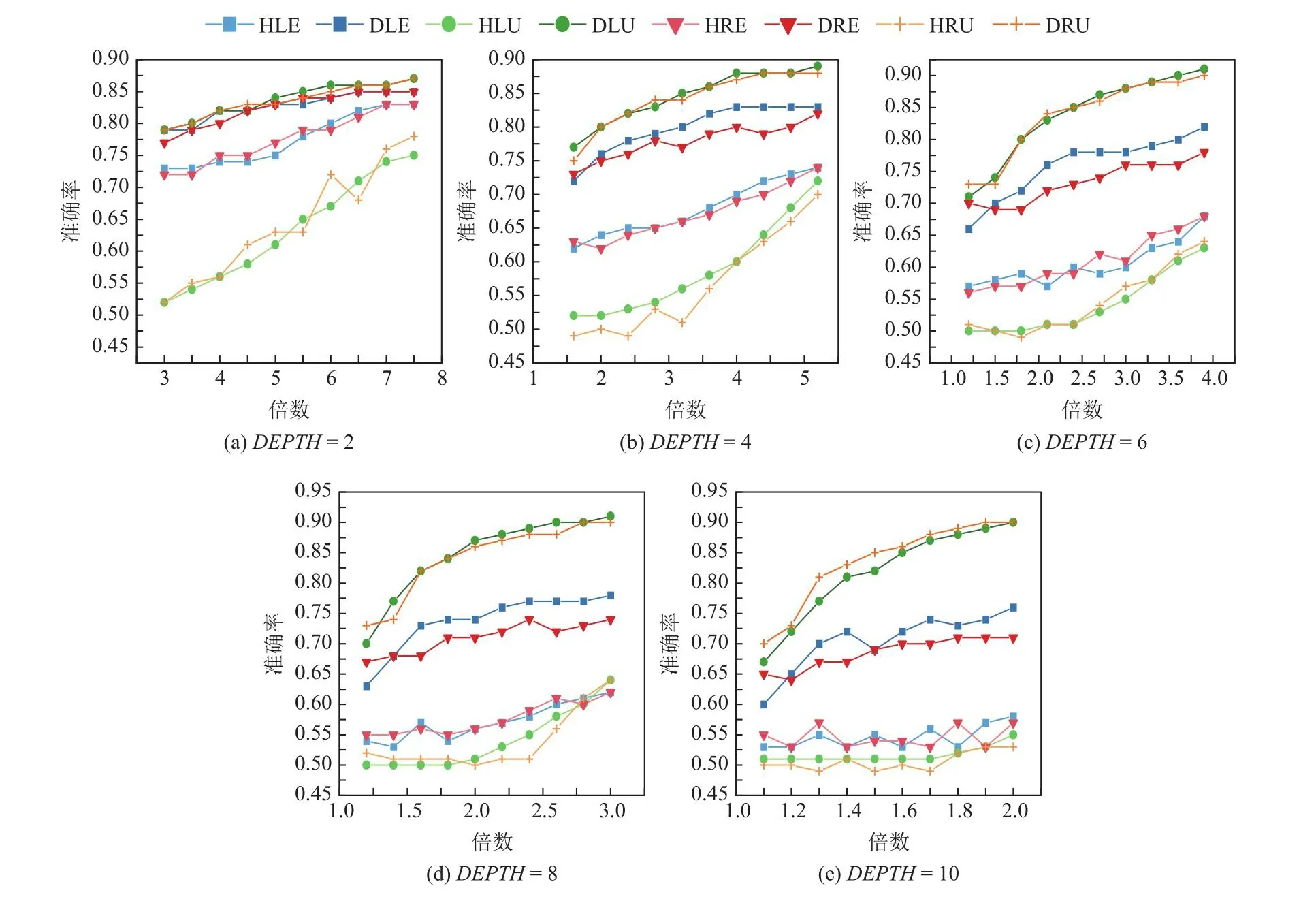
Fig.5 Accuracy of algorithms for depth-varing trees with node gap equals to 0.02图5 节点间隔为0.02时深度变化的树类别的算法准确度

表5设定固定积数的树类别，以观察在树节点数量显著不同的树结构中算法性能的表现.图6和图7分别为固定积数的树类别在节点间隔分别取0.01和0.02时8种算法的性能，可以发现在庞大的树结构中，基于相对熵置信区间的算法类在采样次数小幅度增加时其准确度会显著增加，这表明本文所提的DLV算法类更适用于大规模树结构，以实现节省计算资源的目的.

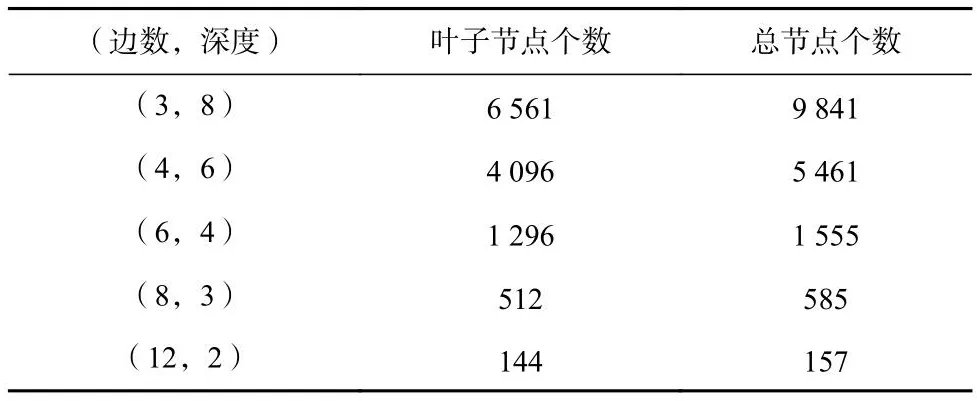
Table 5 Five Fixed Product Tree Structures表5 固定积数的5种树结构

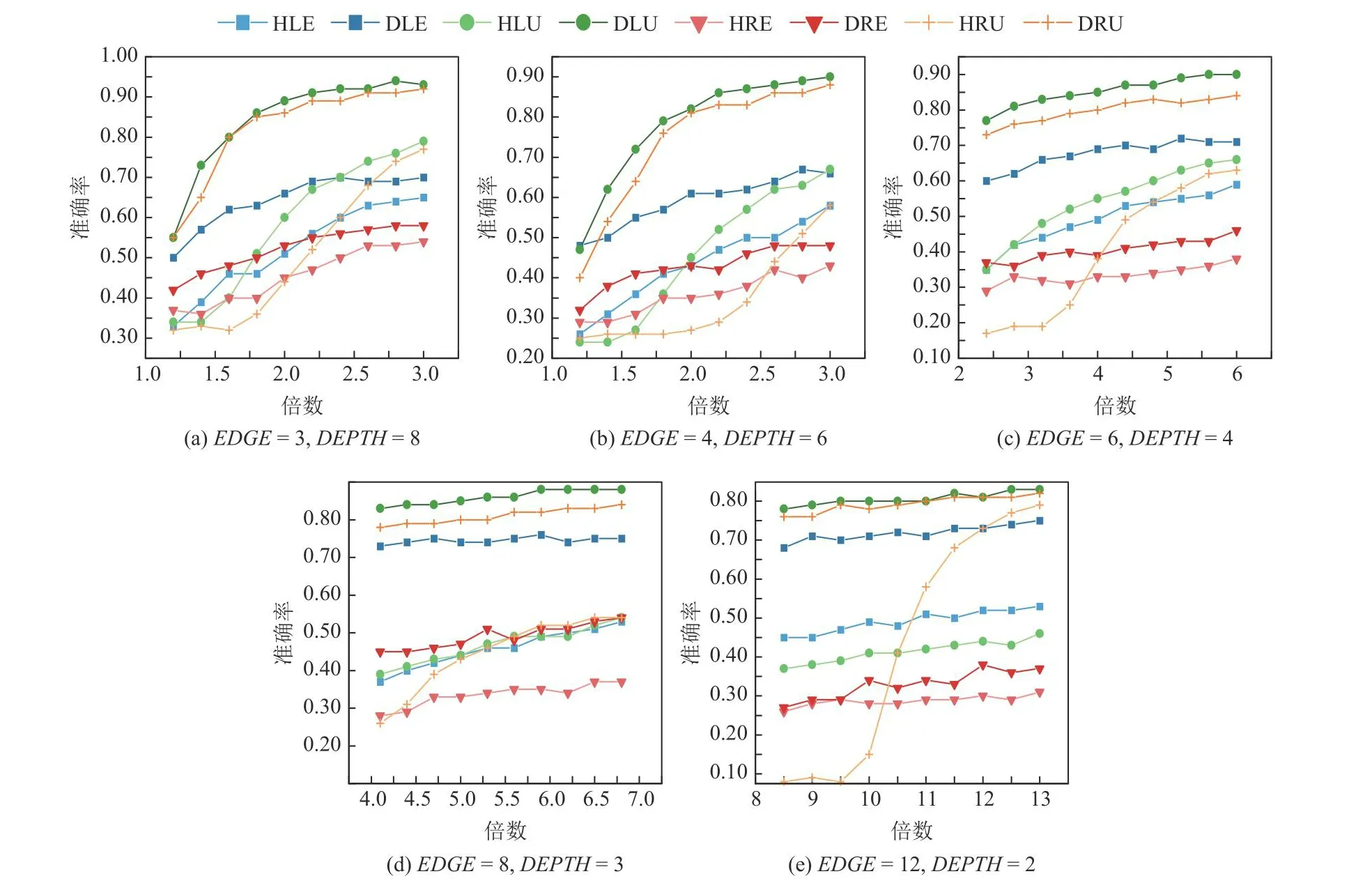
Fig.6 Accuracy of algorithms for fixed product trees with node gap equals to 0.01图6 节点间隔为0.01时固定积数的树类别的算法准确度

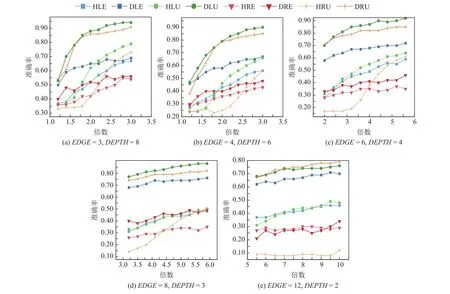
Fig.7 Accuracy of algorithms for fixed product trees with node gap equals to 0.02图7 节点间隔为0.02时固定积数的树类别的算法准确度

同时，通过比较基于RS策略和LUCB策略的算法类可以发现，LUCB策略整体而言具有更高的准确度.这是因为RS策略忽略节点之间的价值差异，对所有第1层节点进行等量采样.而LUCB策略首先计算出2个高价值的备选节点，并对其中不确定性更大的节点进行采样.LUCB策略作为一种启发式方法，避免了对低价值节点进行过度采样造成的资源浪费，在有限的预算内对更有价值的节点进行更充分地探索，因此能获得更好的性能.

设定节点间隔为0.01，表6、表7和表8表示将15种树模型上8种算法的实验性能按照基于相对熵置信区间和基于霍夫丁置信区间进行分类的结果，可以发现本文所提出的构建相对熵置信区间以估计节点取值的方法能够显著提升算法性能.

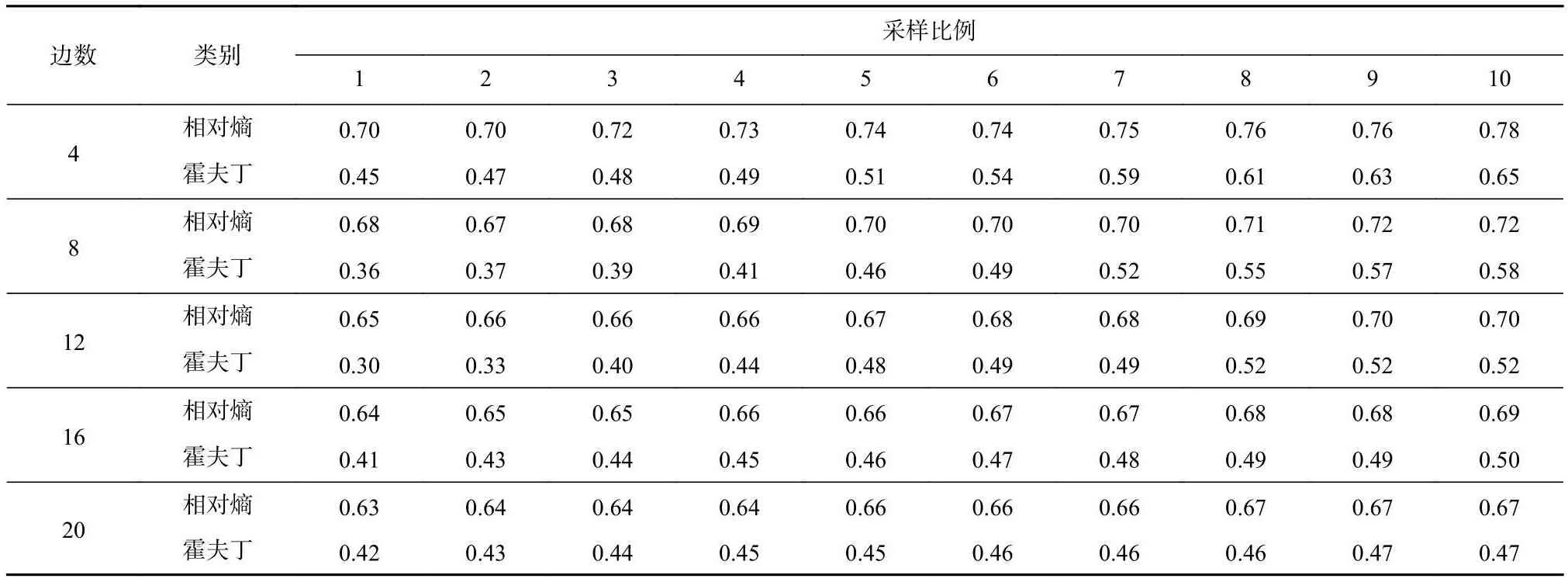
Table 6 Accuracy Comparison of Two Classes of Algorithms for Edge-varing Trees with node gap equals to 0.01表6 节点间隔为0.01的边数变化树上的2类算法准确度对比

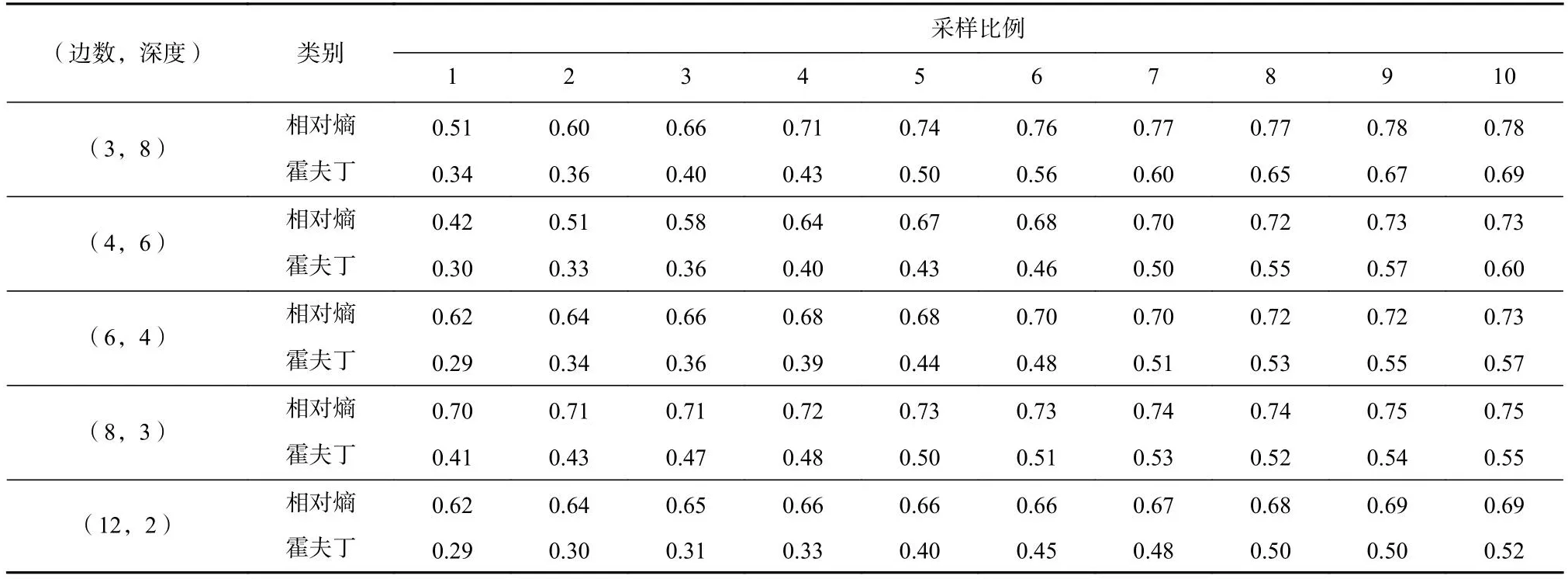
Table 8 Accuracy Comparison of Two Classes of Algorithms for Fixed Product Trees with node gap equals to 0.01表8 节点间隔为0.01的固定积数树上的2类算法准确度对比

5.2 井字棋博弈场景

为了验证DLU算法在实际博弈场景中具有良好的性能，本文引入OCBA-MCTS算法[34]，其完全契合固定预算下最优动作识别问题的最小化识别误差的目标，是目前已知具有正确识别概率下界的最好算法，并在井字棋这一实际博弈场景中表现出优越的性能.

井字棋是一个2名玩家、完全信息、零和博弈游戏.棋盘为3×3大小，共有9个落子点，己方玩家（“O”）和对手玩家（“X”）轮流落子，见图8.当在1行、1列或对角线上出现连续3个相同标记时，标记对应的一方获胜.如果双方都采取最佳行动，游戏将平局结束.本文考虑2种游戏设置： 图9和图10的左图分别表明对手玩家已经在0号位置（设置1）和4号位置（设置2）标记了 “X”.图9和图10的右图分别表明己方玩家在对应设置下的最优动作.由于棋盘的对称性，因此在设置2中己方玩家的最优动作是0，2，6，8中的任意一个位置.如果算法运行结束后返回的动作与最佳位置匹配，则算法识别了一个正确的动作.OCBA-MCTS算法的参数设置与文献[34]保持一致.DLU算法设置参数λ=10，算法重复5 000次观察平均性能.在初次对所有叶子节点进行估值时，使用探索函数：α(n,λ)=log(λ)+1.5log(log(n)+1)，其后计算置信区间时使用探索函数:

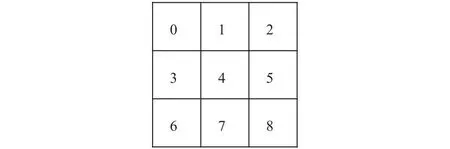
Fig.8 Tic-tac-toe board图8 井字棋棋盘

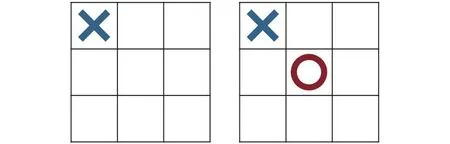
Fig.9 Tic-tac-toe game setup 1图9 井字棋游戏设置1

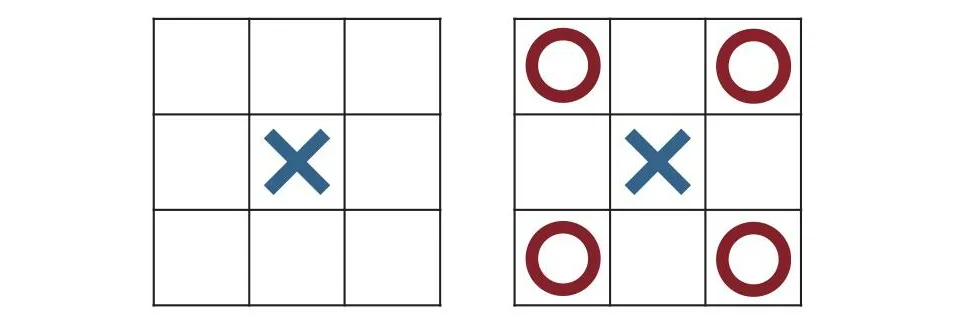
Fig.10 Tic-tac-toe game setup 2图10 井字棋游戏设置2

图11和图12分别为DLU算法和OCBA-MCTS算法在2种游戏设置下的实验结果，2个算法性能相近，都能够有效地识别最优节点.然而，OCBA-MCTS除了理论分析中的分布假设难以保证外，该算法在选择流程中，需要计算当前节点下的每个子节点的新采样分配，进而确定采样节点，因此运行时间较为缓慢.当任务模型状态空间越大，该算法的时间消耗将是一个不能忽视的问题.DLU算法使用的最优节点选择策略相比更加简洁，具有更低的时间复杂度.

Fig.11 Accuracy of algorithms under setup 1图11 设置1下的算法准确度

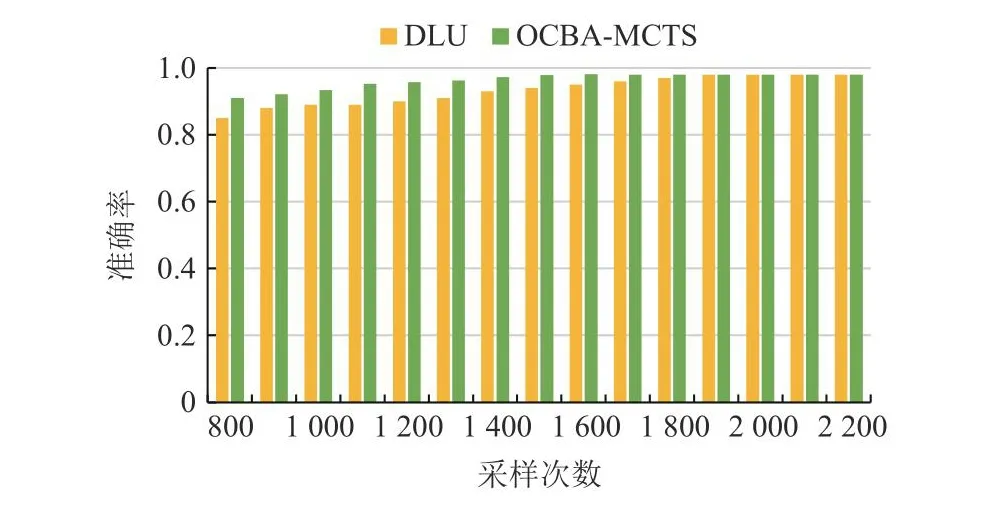
Fig.12 Accuracy of algorithms under setup 2图12 设置2下的算法准确度

6 结 论

为了解决固定预算下的MCTS最优动作识别问题，本文构造了极小极大采样树抽象模型MST并提出了基于相对熵置信区间的DLU算法，其包含与MST模型估值、回溯和选择3个流程对应的3个部分：叶子节点胜率估计、第1层节点值估计、最优节点选择.同时，本文给出了最优动作的识别误差上界，并通过在30个树模型上的实验验证了基于相对熵的算法类在准确性上具有显著优势.

在未来的工作中，将基于非平稳多臂赌博机对MCTS最优动作识别问题的采样次数和误差进行分析，从而更加还原MCTS流程，使得分析结果与实际算法更加匹配.同时，对强化学习的主要算法存在的随机一致性[40-41]进行性能分析，以指导生成更具有泛化性、可解释性的新方法，也是未来值得关注的研究方向.

作者贡献声明：刘郭庆提出了算法内容并撰写论文；钱宇华指导并完善论文；张亚宇和王婕婷提出了修改意见并修改论文.