基于ACO-ENN 算法的高压直流输电线路故障测距技术

李 迎

（国网江苏省电力工程咨询有限公司（国网江苏省电力有限公司建设分公司），江苏 南京 210011）

0 引 言

电力系统中，高压直流电线路承担着电能传输的任务，具有承载容量大、节点连接简单以及传送距离远等特点，在我国发展前景非常广阔。我国地域辽阔，地形条件复杂，输电线路通常会受各种自然环境、地形以及气候等因素的影响，极易引发系统故障，高压直流输电线路故障不仅会制约我国社会经济的发展，还会影响电力系统正常运行[1]。精确定位故障点，有助于减少线路查找的物力和人力，及时实现故障处理，降低由于停电引发的经济损失[2]。因此，探究可靠、精确的线路故障测距算法，可为输电线路稳定安全运行提供保障。Elman 动态神经网络（Elman dynamic Neural Network，ENN）数据拟合能力比较强，其自身也存在反馈结构，因此将固有频率2 倍频与主频频率、幅值等当作网络输入训练样本，同时将故障距离当作网络输出训练样本，基于ENN 计算高压直流输电线路故障测距。选择蚁群优化（Ant Colony Optimization，ACO）算法优化ENN 阈值和权值，通过MATLAB 与PSCAD 软件展开联合仿真，研究结果显示基于ACOENN 算法的输电线路故障测距具有较高的可靠性、测距精度以及稳定性。

1 固有频率故障测距法

1.1 故障测距法

通常在高压直流输电线路发生故障时，初始行波会在系统与故障点间持续反射，形成故障行波，从频域上看就是一系列谐波，也就是故障行波固有频率。基于电流函数公式，将固有频率、边界条件与故障距离的关系表示为

式中：d为故障距离；v为行波传播速度；s虚部为固有频率，实部为行波衰减系数。边界条件主要分为故障点反射系数（即a2）与测距点反射系数（即a1），用公式表示为

式中：Zs为系统输电侧的阻抗；ZF为故障位置阻抗；Zc为线路传输阻抗。求解式（1），得出

式中：aM、aF表示a1与a2所对应的反射角。分析故障行波频谱发现，频谱内首个峰值对应幅值达到最大，与该频率相对应的是主频，本文提取主频对故障测距算法展开研究。

1.2 可行性分析

在高压直流输电系统内部，母线出现比较少，极易提取故障行波暂态信号[3]。因此，自暂态信号内进行固有频率的提取，计算固有频率和故障距离的函数关系，以计算故障距离。图1 为暂态行波频谱。

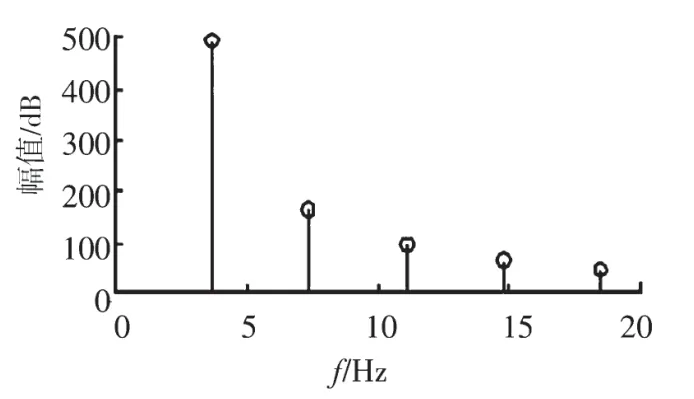
图1 暂态行波波形、频谱

分析图1 可知，故障行波传播输电线路时，其幅值会呈衰减态势，且波头畸变严重，自时域内很难将行波波头提取出来[4]。本文自频域角度展开测距，有效避免了由于识别反射波头产生的误差。即使图1 内故障行波波头畸变与衰减状态下，也可将精准固有频率提取出来，因此该测距方法具有较高稳定性与可靠度。

2 ENN 分析

2.1 神经网络

ENN 在反馈网络中具有代表性，最初的ENN 主要功能在于处理语音，且ENN和普通网络存在差异性，不仅具备隐含层、输入层以及输出层，而且增加了特殊联系单元，特殊联系单元能够用于存储隐含层的历史输出数据，因此将该单元叫作结构层，ENN 具备动态记忆功能[5]。图2 为ENN 的结构。

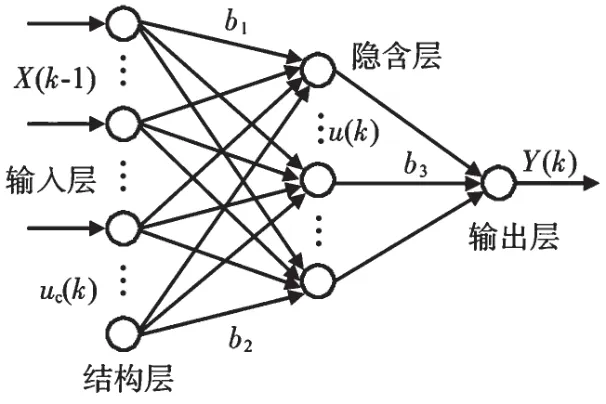
图2 ENN 的结构

分析图2可知，网络结构主要包含结构层、输入层、隐含层以及输出层，其中结构层可存储隐含层的历史输出值，能够自隐含层对反馈信号进行接收，在延迟存储后输入隐含层，由此不仅能够提升网络的动态信息处理能力，而且能够增强其对历史数据的敏感性。网络结构中，输出层具有线性加权功能[6]。

2.2 ENN 的数学模型和学习算法

ENN 结构图中，b1表示隐含层与输入层之间的权矩阵，b2表示隐含层与特殊联系单元之间的权矩阵，而b3则表示隐含层与输出层之间的权矩阵，由此获得ENN 数学模型，用公式表示为

式中：f(·)表示结构层传递函数，一般采用Sigmiod函数；而g(·)则表示输出层传递函数，一般采用线性函数。具体表达公式为

假设系统的第N步输出函数为yd(x)，那么系统目标函数，也就是误差函数用公式表示为

图3 为ENN 学习算法流程图。

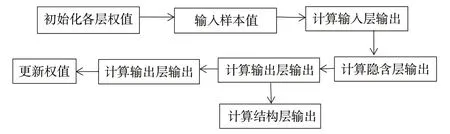
图3 ENN 学习算法流程图

2.3 ACO-ENN 优化算法

在ENN 中，信息素发挥是蚂蚁交流信息的一种基本方式，该方式对蚂蚁生活极为重要。通过逐步分析蚂蚁觅食行为发现，觅食期间，蚂蚁通常会通过信息素相互写作，以形成所需正反馈，确保各路径蚂蚁可以在最短路径收敛。未经优化情况下，ENN 网络训练过程中极易陷入局部最优解，尤其是收敛速度不理想，缺乏确保系统稳定性，这就需要优化处理ENN 初始权值和阈值。选择ACO 算法优化ENN，能够有效防止ENN 陷入局部最优解现象，缩减训练频率和时间，同时有助于故障测距精确度与收敛速度的提升。

3 仿真试验与结果

3.1 仿真试验

ENN 训练前必须提取输入输出训练样本，因此需要考虑到样本约束条件及其特征，所选样本既要考虑故障模式，又要符合ENN 训练条件。此次试验选择PSCAD 软件对高压直流输电线路模型进行搭建，具体见图4。

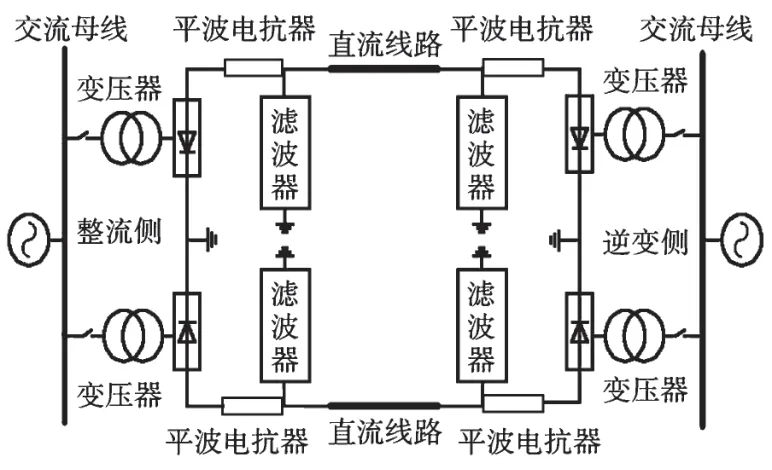
图4 输电线路模型

线路模型中，线路总长度设为800 km，传输电流、电压分别是2.5 kA、±600 kV，设施线路平波电抗为0.35 H。线路滤波器选择双调谐模式，再对线路模拟仿真，获得测量端电压，通过后向预测Prony 算法将二倍频、主频提取出来当作样本属性，能够获得2 000组数据，随机抽选其中的1 500组当作模型训练，其他500 组数据当作模型检验。通过MATLAB 软件仿真原始ENN 和ACO 优化后的网络，得到如图5、图6 所示的误差曲线。

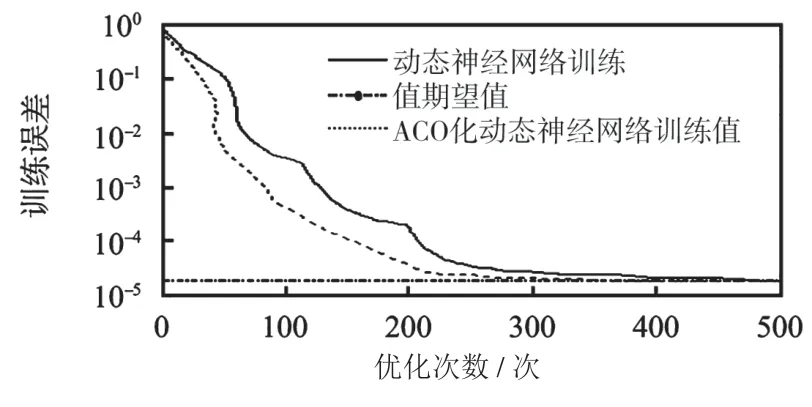
图5 ACO 动态神经网络与ENN 收敛曲线

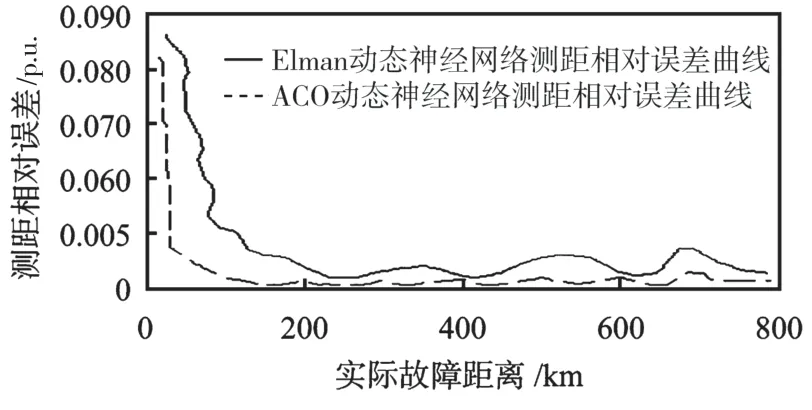
图5 ACO 动态神经网络与ENN 相对误差

ACO 优化后，分析相对误差曲线可以看出，蚁群算法优化后在很大限度上提升了测距误差平稳性，同时缩减了误差值。首端故障发生过程中，误差值较大，可达8.7%，主要是因为首端故障降低了固有频率精度。首端故障发生后，测量终端母线与故障点的行波频率较高，导致行波衰减速度较快，而且对面端反射行波也会对被测端频率提取产生影响。

3.2 试验结果

基于ACO-ENN 进行高压直流输电线路的故障测距，以5 个故障点当作试验点，测距结果受过渡电阻制约，因此试验中所选过渡电阻不同，分别采用0 Ω、40 Ω、80 Ω 的过渡电阻，依照所设参数得出故障测距数值，见表1。

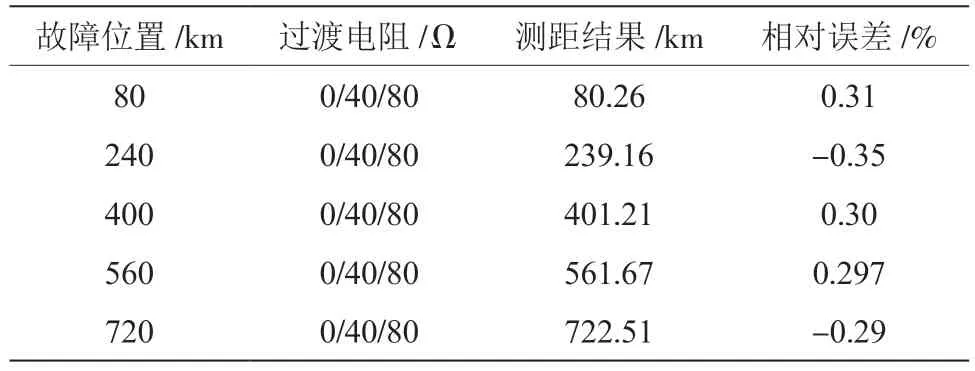
表1 高压直流输电线路故障测距结果

分析表1 可知，网络优化后能够达到精准测距，故障测距时，故障测距精度受过渡电阻影响比较小，虽然测距精度会随距离增加而有所降低，但在600 ～800 m 中，可控制测距精度为±0.4%。因此，通过该方法展开高压直流输电线路故障测距，具有良好的鲁棒性和稳定性。

4 结 论

在高压电流输电线路故障测距中，应用ACOENN 能够在很大限度上提升网络收敛速度和精确度，因为ACO算法鲁棒性比较强，并实现全局最优解搜索，所以该方法有助于提高网络训练收敛速度，防止陷入局面最优。因此，ACO-ENN 算法可在直流输电线路故障测距领域应用与推广。