功率循环载荷下BGA 焊点应力与应变分析

高超，黄春跃，梁颖，刘首甫，张怀权

(1.桂林电子科技大学,桂林,541004；2.成都大学,模式识别与智能信息处理四川省高校重点试验室,成都,610106；3.成都航空职业技术学院,成都,610021；4.工业和信息化部电子第五研究所,广州,511370)

0 序言

随着集成电路制造业的快速发展，封装器件集成度持续提升，I/O 引脚数的急速增加使封装器件功耗越来越大,对集成电路封装要求变得更加严格[1].作为集成电路封装主要方式之一的球栅阵列封装(ball grid array，BGA)使每平方英寸的存储量大幅度提升，并且具有体积小、散热性能及导电性能更好的优势被广泛应用在电子产品中[2].含有BGA 封装的电子器件在使用过程中，周期性的通电、断电会使器件承受不同的功率载荷，器件内部的热流密度也会产生周期性的变化，因此，器件在服役时必然重复承受通电升温和关断降温的循环过程[3].由于芯片、基板、BGA 焊点及塑封材料之间的存在着热膨胀系数失配问题，在温度变化的情况下会致使BGA 焊点承受周期性循环变化的应力与应变，产生热疲劳损坏，导致整个封装器件失效[4-5].

因此，应该重视由高低功率载荷而导致的包括BGA 焊点在内的各种互连焊点的失效问题.国内外学者针对互连焊点在功率载荷下的可靠性已开展了相关研究，如王强等人[6]分析了芯片尺寸封装(chip size package,CSP)焊点在给定功率循环载荷下的应力与应变，结果表明，应力最大焊点位于阵列的最外侧，从而确定了关键焊点位置.王建培等人[7]分析了在热功率载荷下阵列中不同位置BGA 焊点的应力分布情况，并采用响应曲面法和遗传算法相结合的优化方法完成对BGA 焊点结构参数的优化.Huang 等人[8]构建涵盖高低温蠕变特性的新型SnAgCu 钎料本构模型，通过该模型模拟功率模块内部芯片中SAC305 焊点的循环蠕变变形情况，结果表明，蠕变累积应变和蠕变应变能密度估算焊点的热疲劳寿命更接近试验结果.Junghaenel 等人[9]研究了功率脉冲持续时间对封装器件焊点可靠性的影响，并通过功率循环测试分析了芯片互连焊点热疲劳失效机制，失效分析表明芯片的横向温度梯度对焊点疲劳有显著影响.Karppinen 等人[10]分析了在固有频率下功率载荷对焊点断裂模式的影响，结果表明，在固有频率下，功率载荷会加快焊点裂纹的扩展，降低元器件服役可靠性.以上研究结果一方面表明了功率载荷对焊点可靠性的影响显著，另一方面也反映出国内外学者针对功率循环载荷下焊点应力的研究尚有不足，例如尚无针对性的研究功率循环载荷下焊点结构参数对焊点应力影响的显著性，未建立焊点应力与结构参数的量化评价模型，进而提高互连焊点的服役可靠性.

以BGA 焊点为研究对象，基于ANAND 本构方程对功率循环载荷下BGA 焊点的应力与应变进行有限元分析，搭建试验平台完成功率循环载荷下器件应力与应变的测量，验证仿真分析的可行性，并分析焊点直径、焊点高度、焊盘直径、FR4 基板厚度对焊点应力的影响大小及显著性，基于回归分析构建了焊点功率循环应力的量化评价模型，为实际工程应用中提高BGA 焊点在功率载荷下的可靠性提供一定的理论指导.

1 功率循环载荷有限元分析

1.1 BGA 焊点分析模型

建立BGA 焊点仿真分析模型时，参考了由Hynix 公司生产的H5TC2G63 GFR-PBA 型封装器件，仿真分析模型由FR4 基板、铜焊盘、BGA 焊点和芯片4 部分组成，如图1 所示.

图1 BGA 焊点模型Fig.1 BGA solder joints model

对模型施加功率循环载荷进行仿真分析时假定焊点无空穴和气孔等缺陷[11].模型中共有96 个焊点，焊点材料选用无铅钎料SAC387，FR4 基板尺寸为21 mm × 17.5 mm × 1 mm，芯片尺寸为13 mm ×7.5 mm × 0.76 mm，焊点间距为0.8 mm，焊点径向尺寸为0.45 mm，上、下焊盘直径均为0.32 mm，焊盘高度为0.02 mm，焊点高度为0.33 mm，模型中不同结构材料参数如表1 所示.

表1 材料参数Table 1 Material parameters

为了准确模拟BGA 焊点模型中焊点在功率循环载荷下的应力响应，采用ANAND 本构模型描述焊点的变形行为，SAC387 钎料ANAND 模型参数如表2 所示[12].对BGA 焊点模型进行有限元网格划分时，采用映射网格划分方式对模型进行网格划分，并对BGA 焊点、铜焊盘与芯片和FR4 基板接触部位进行网格细化，模型网格划分后单元数为143 392 个，节点数为181 242 个.

表2 SAC387 钎料ANAND 模型参数[12]Table 2 SAC387 solder ANAND model parameters

1.2 功率循环载荷下焊点应力分析

采用热-结构间接耦合方法对BGA 焊点模型完成加载分析.即首先进行热分析，BGA 焊点模型中所有结构均选用热单元SOLID70，以功率密度的形式对芯片施加功率循环的热源，在BGA 焊点模型的外表面设置空气的对流换热系数，其值为10 W/(m2·K)，零应力参考温度为20 ℃，得到模型温度场.然后再进行结构场分析，将BGA 焊点单元类型转为粘塑性单元VISCO107，其余结构单元类型转为结构单元SOLID185，把热分析结果作为体载荷施加到模型中进行分析，边界条件为FR4 基板底面4 个角点为全约束，得到BGA 焊点在功率循环载荷下的范式等效应力与应变.

考虑到H5TC2G63GFR-PBA 型封装器件的实际工作温度为0～ 85 ℃，施加功率循环载荷时，设置如图2 所示的功率密度加载曲线.启动电源时功率密度由0 上升到9.6 × 106W/m3，待机时功率密度 由 9.6 × 106W/m3下 降 到1.2 × 106W/m3，高、低功率运行时间均为20 min，升、降功率时间均为10 min，此为一个周期，共6 个功率循环加载周期.

图2 功率循环加载曲线Fig.2 Power cycle loading curve

对BGA 焊点模型施加功率循环载荷，焊点内部范式等效应力随时间变化曲线如图3 所示.由图3可知，BGA 焊点内的范式等效应力随时间累积增加，在低温保温开始时，焊点内的范式等效应力达到最大，而在高温保温结束时，范式等效应力达到最小，焊点内的应力随循环加载曲线作周期变化.功率循环加载过程中高低功率对应的焊点阵列温度云图如图4 所示，高功率加载时焊点阵列温度为83.821 ℃，低功率加载时焊点阵列温度为32.353 ℃，符合H5TC2G63GFR-PBA 型封装器件的实际工作温度范围.

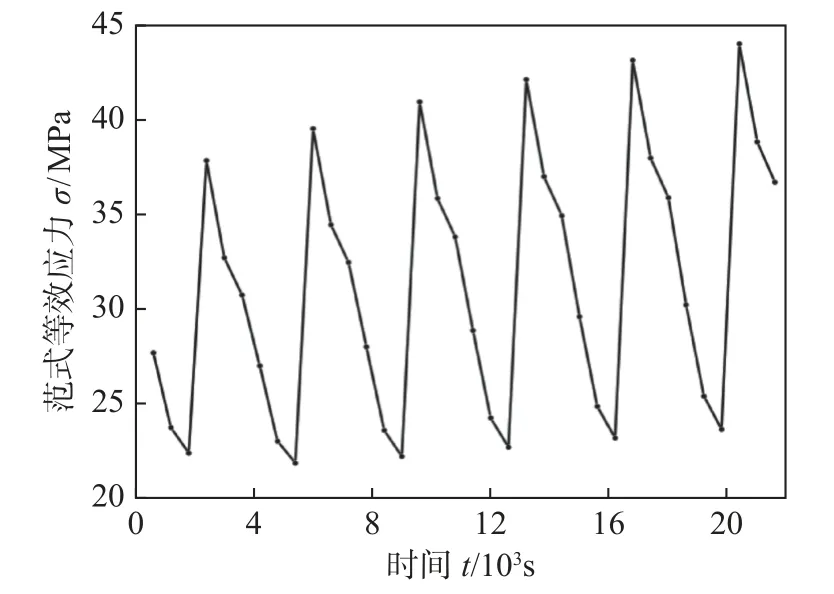
图3 BGA 焊点等效应力曲线Fig.3 Equivalent stress curve of BGA solder joints

图4 BGA 焊点阵列温度云图Fig.4 Temperature cloud of BGA solder joints.(a) low power solder joints;(b) high power solder joints

BGA 焊点模型在功率循环加载过程中，6 个循环后BGA 焊点应力应变幅趋于稳定，因此选择第6 个循环过程读取BGA 焊点的范式等效应力和等效塑性应变，等效应力与应变分布图如图5 所示.

图5 BGA 焊点应力与应变分布Fig.5 Stress and strain distribution of BGA solder joints.(a) stress distribution;(b) strain distribution

由图5 可见，功率循环载荷下BGA 焊点应力与应变在焊点阵列中呈不规则状态分布，焊点应力与应变从阵列内侧向外侧逐渐增大，位于阵列边角处焊点的应力与应变最大.BGA 焊点最大应力为43.991 MPa，最大应变为0.010 422.单个焊点内部的应力与应变也呈不均匀状态，但焊点内应力与应变的变化趋势一致，均是从焊点内中间部位向焊点外围曲面逐渐递减，向端面两侧逐渐递增，最大应力与应变出现在焊点与PCB 铜焊盘的连接处，长期的应力与应变集中会使该处产生裂纹，导致焊点与铜焊盘剥离，影响器件服役的可靠性.

2 功率循环加载试验分析

文中设计了元器件功率循环应力与应变测量平台，通过试验分析验证仿真分析的可行性.制作试件并采用应变片完成功率循环应力与应变的测量，获得试验数据后计算与仿真数据之间的相对误差，完成试验验证.

2.1 应变片公式基本原理

试验过程中采用直角应变片测量应变，通过应变仪直接测出0°,45°和90°方向的线应变，分析平面应变状态可知，测试点处任一方向的线应变为[13]

式中：εθ为任意角度方向的应变；εx为x方向的应变；εy为y方向的应变；γxy为xOy平面的剪切应变.

分别把θ=0°，θ=45°和θ=90°代入式(1)，可求得x，y方向的应变与xOy平面的剪切应变.

仿真分析时，FR4 基板平面置于xOy平面，在平面应力状态分析中，应变和应力方向一致.根据广义胡克定律，基于式(5)～ 式(7)求出测试点处x，y方向应力及xOy平面内剪切应力.

式中：σx为x方向的应力；σy为y方向的应力；τxy为xOy平面内的剪切应力；E为材料的弹性模量；μ为泊松比.

2.2 试验结果与分析

制作与图1 所示仿真模型相同的测试试件并在测试点处粘贴应变片完成功率循环应力与应变的测量.试件上共粘贴3 个应变片，放置位置如图6 所示，粘贴应变片的试件如图7 所示.获得测试点处试验分析结果，与仿真模型上相同位置处的仿真分析结果进行对比.

图6 应变片放置位置示意图Fig.6 Position diagram for the strain gauge

图7 BGA 焊点试件Fig.7 BGA solder joints test sample. (a) before applying the strain gauges;(b) after applying the strain gauges

搭建的BGA 元器件试验样件功率循环应力与应变试验测量平台如图8 所示.试验平台包括：试件(含直角应变片和陶瓷加热片) ①、继电器②、直流稳压电源③、示波器④、应变测量显示界面⑤、动态应变仪⑥和信号输入线⑦.

图8 功率循环试验测量平台Fig.8 Experimental measurement platform for power cycle

通过动态应变仪测得的试验样件在测试点处0°，45°及90°方向的应变数值，根据式(1)～ 式(7)计算得出测试点处x，y方向应力值及xOy平面剪切应力值如表3 所示.

表3 试验测试值与仿真值对比Table 3 Simulated and measured values

由表3 可知，在功率循环载荷下，试验样件测试点1 处x，y方向应力以及xOy平面剪切应力试验测试值，与仿真模型中相同位置处仿真值的相对误差分别为12.37%，11.28%，9.81%.测试点2 处x，y方向应力以及xOy平面剪切应力试验测试值，与仿真模型中相同位置处仿真值的相对误差分别为10.49%，11.89%，9.46%.测试点3 处x，y方向应力以及xOy平面剪切应力试验测试值，与仿真模型中相同位置处仿真值的相对误差分别为11.93%，11.14%，9.07%.3 个测试点处的相对误差值均小于15%，即通过试验测试进一步证明了仿真分析的可行性.

3 模型结构参数分析

模型结构参数的改变会直接影响BGA 焊点在功率循环载荷下的应力，为有效降低BGA 焊点在功率循环载荷下的应力，提高元器件在服役时的可靠性.对BGA 焊点模型结构参数进行正交试验，结构参数包括FR4 基板厚度、焊点高度、焊点直径和焊盘直径.通过极差分析和方差分析确定了BGA 焊点应力最低结构参数组合和应力影响显著因素，获得最优参数水平组合，并基于回归分析构建BGA 焊点功率循环应力的量化评价模型.

3.1 正交试验组合设计

正交试验法可用于影响元器件焊点可靠性因素的分析[14-15]，基于正交表确定BGA 焊点仿真试验组合时，固定焊点材料为无铅钎料SAC387，在焊点模型结构参数中选取FR4 基板厚度δP、焊点高度HS、焊点直径DP和焊盘直径DS为4 个可控因素，每个因素确定4 个水平值，表4 为不同因素水平表.基于L16(44)正交表获得16 组不同因素水平试验组合，如表5 所示.分别建立16 组BGA 焊点仿真模型完成功率循环加载分析，不同参数水平组合的BGA 焊点最大应力值如表5 所示.

表4 因素水平表Table 4 Factor level table

表5 正交设计试验Table 5 Orthogonal design test

3.2 功率循环应力极差与方差分析

根据表5 中的正交试验数据，对BGA 焊点在功率循环载荷下的应力作极差分析与方差分析，获得BGA 焊点应力最低的结构参数组合，并确定各个结构参数对BGA 焊点应力影响大小排序及影响是否具有显著性.BGA 焊点功率循环应力极差分析结果与方差分析结果如表6 和表7所示.

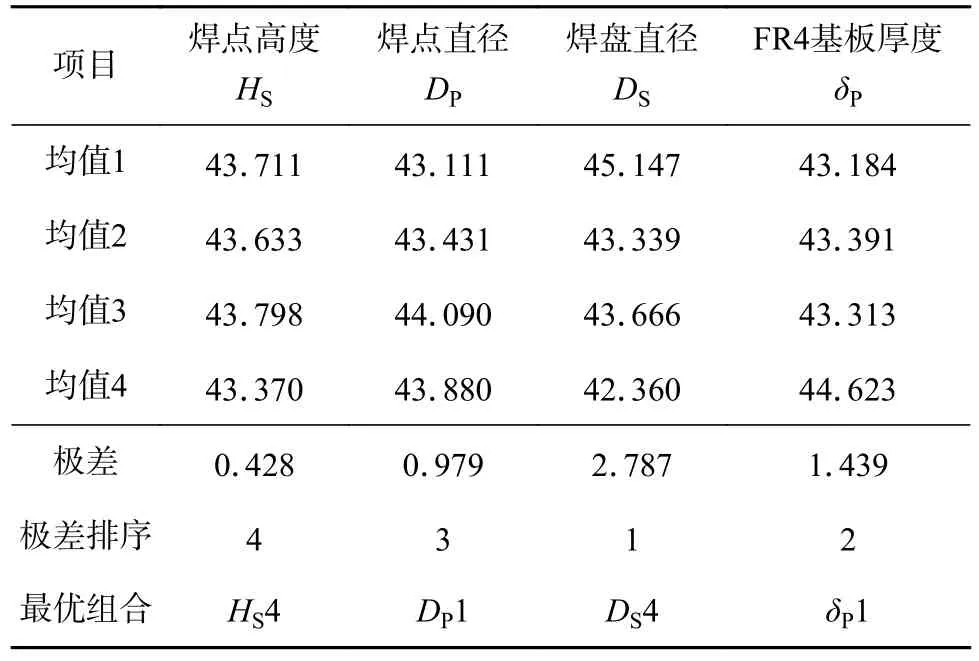
表6 极差数据分析Table 6 Analysis of range data

表7 方差数据分析Table 7 Analysis of variance data

由表6 可知，BGA 焊点仿真模型在功率循环载荷下，选取的4 个结构参数HS，DP，DS和δP的极差值分别为0.428，0.979，2.787 和1.439，极差值大小排序为：DS，δP，DP，HS，因此这4 个因素对BGA 焊点功率循环应力影响力排序为DS，δP，DP，HS；根据4 个因素均值数据，取每个因素最小均值得到最优结构参数组合为HS4，DP1，DS4，δP1，即焊点高度0.39 mm，焊点直径0.42 mm，焊盘直径0.34 mm 和FR4 基板厚度0.8 mm.

由表7 可知，置信度为95%时的F 临界值κ为9.280，4 个模型结构参数HS，DP，DS和δP的F 值f分别为0.297，1.698，11.637 和3.906，f大小排序为DS，δP，DP，HS，表明选取的4 个因素对BGA 焊点功率循环应力影响力排序为DS，δP，DP，HS，此分析结果与极差分析结果一致.其中DS的F 值f大于F 临界值κ，HS，DP，和δP的F 值f小于F 临界值κ，因此在置信度为95%时，焊盘直径对BGA 焊点功率循环应力具有显著性影响，焊点高度，焊点直径和FR4 基板厚度对BGA 焊点功率循环应力不具有显著性影响.

为验证BGA 焊点模型最优结构参数组合的正确性.固定焊点材料为SAC387，选取焊点高度0.39 mm、焊点直径0.42 mm、焊盘直径0.34 mm和FR4 基板厚度0.8 mm 建立仿真模型，对模型施加热功率载荷完成分析.分析结果如图9 所示.

图9 最优参数组合焊点应力与应变分布Fig.9 Distribution of stress and strain at the solder joint under the optimal conditions.(a) stress;(b) stress

由图9 可知，最优参数组合的BGA 焊点功率循环等效应力最大值为41.528 MPa、塑性等效应变最大值为0.008 507 2，与1.2 节仿真分析时BGA焊点功率循环等效应力最大值43.991 MPa 相比减小了2.463 MPa，与塑性等效应变最大值0.010 422相比减小了0.001 914 8；与正交试验设计中等效应力值最小组合的41.843 MPa 相比，相差了0.315 MPa，达到了BGA 焊点结构参数的优化目的.由此证明,基于正交设计试验极差分析优化BGA 焊点模型结构参数的合理性和正确性.

3.3 功率循环应力量化评价模型

回归分析能够从多组数据出发确定变量之间的定量关系式[16]，为了确定功率循环载荷下BGA 焊点应力与模型结构参数之间的定量关系，以BGA 焊点模型结构参数为自变量、BGA 焊点应力为因变量，采用多元非线性回归分析对模型各结构参数BGA 焊点应力进行定量描述，得到BGA 焊点应力量化评价模型并进行显著性检验.

对表5 中BGA 焊点模型不同因素水平组合数据及BGA 焊点功率循环应力进行多元非线性回归拟合，充分考虑焊点高度HS、焊点直径DP、焊盘直径DS和FR4 基板厚度δP这4 个因素之间的线性、交互作用和平方项对其进行了正交非线性回归，得到BGA 焊点功率循环应力与焊点高度HS、焊点直径DP、焊盘直径DS和FR4 基板厚度δP的多元非线性量化评价模型为

为了确保BGA 焊点应力量化评价模型的可靠性，完成对模型(8)的方差分析和显著性检验，有关评价指标如表8 所示.

表8 响应面分析结果Table 8 Analysis results of response surface

由表8 可知，BGA 焊点功率循环应力量化评价模型的概率p小于0.000 1(通常小于0.05 表示该项显著)，表明该模型的拟合效果明显；量化评价模型决定系数R2为0.814，进一步表明该模型具有良好的拟合度.以上分析结果说明量化评价模型能够准确拟合如表5 所示.

在检查了BGA 焊点应力量化评价模型的显著性后，为进一步证明模型的可信度，将表5 中不同结构参数水平值代入量化评价模型，计算BGA 焊点应力值，将计算出的预测值与BGA 焊点应力仿真值进行对比，结果如图10 所示.由图10 可知，16 组数据的误差率均低于3%，其中第5 组数据误差率最大为2.681%，其余数据误差率均低于2%，证明了该量化评价模型的预测准确率与有效性.

图10 评价模型预测值和仿真值对比Fig.10 Comparison of predicted and simulated values of the evaluation model

4 结论

(1) 在功率循环载荷下，BGA 焊点内部应力与应变分布不均，从焊点中间部位向外围曲面递减，向端面两侧递增，焊点与PCB 铜焊盘的连接处应力最大，长期的应力与应变集中会使该处产生裂纹.

(2)功率循环载荷下BGA 焊点模型结构参数最优水平组合为焊点高度 0.39 mm、焊点直径0.42 mm、焊盘直径0.34 mm 和 FR4 基板厚度0.8 mm，最优组合下焊点应力与应变明显降低；4 个参数对焊点应力影响大小排序为：焊盘直径、FR4 基板厚度、焊点直径、焊点高度，其中焊盘直径对焊点应力影响显著.

(3) 通过非线性回归分析得到高拟合度的BGA 焊点功率循环应力量化评价模型，可以精确表达焊盘直径、焊点高度、焊点直径、FR4 基板厚度与焊点应力间的定量关系.