游戏背后思考的力量
郭燕玲 黄家林

【摘 要】在常态化教学过程中,不仅要彻底改变“学”与“教”的关系,而且要摆脱接受式学习、机械训练等传统教学方式,以学生的发展为本,游戏化、实验化的教与学方式无疑是较为有效的手段。把抽象的数学学习内容变成充满趣味性的主题游戏与数学实验活动,不仅能激发学生的学习兴趣,让学生在玩中学、做中悟,而且改变了教师课堂教学过于注重知识传授的方式。从而使课堂向培养思维能力、学科核心素养、构建新的实践型学习与育人方式转变。
【关键词】跨学科融合 游戏化 数学实验 思考力 核心素养
新课标倡导游戏化、生活化、活动化的“学”与“教”方式,给常态化课堂教学提出了要求,同时也指明了方向。对此,教师也有了新的思考:
问题1:面对小学生对数学抽象性的认知困难,如何发挥游戏在数学教学和课程体系建设中的作用,落实核心素养培养目标?
问题2:如何在常态化的教学中设计出符合小学生年龄特点的实验活动,让他们在真实的生活情境中经历学习的过程,真正感受到数学好玩、数学好用?
笔者从以下几个方面进行了尝试与探索。
一、游戏化学习“看见”思考的轨迹,“看见”思考的力量
以“小思考家”思维游戏课“提前计划——寻宝探险”的教学为例:
该课程以游戏“寻宝探险”创设情境,通过“掌握规则—经历任务—规划路线—利用资源—达成目标(获得宝藏)”等环节开展教学。
教学目标:在经历任务、规划路线、达成目标的环节中,通过自主尝试、主动思考,总结概括问题解决的策略,培养学生有序思考、理性分析的思维能力,逐渐建构问题解决的思维模型。
(一)利用智能课件“人机对话”,自主学习,主动思考
在学习游戏规则时,教师通过播放视频、智能提问等方式让学生自主学习规则,并通过智能课件预设问题,在辅助加深对游戏规则理解的同时,引发学生主动思考。这不仅能帮助学生熟练运用规则,开展游戏,还能让课堂充满趣味性、互动性,最大限度地提高学生的专注力与参与度。
(二)经历任务将思维过程“可视化”,“看见”思考的轨迹
(1)角色扮演——经历任务过程:让学生做游戏中的“寻宝奇兵”,学生仿佛身临其境,充满挑战的激情和获胜的欲望。
(2)规划路线——“看见”思考的轨迹:通过动画分解游戏过程,展现出“寻宝奇兵”的寻宝路线,引导学生体会“寻宝奇兵”中寻找宝藏的过程就是我们的思考过程;寻宝路线就是我们的思考轨迹。
(三)有序思考获得宝藏,“看见”思考的力量
通过学习思考法则“铺路策略”帮助学生掌握正确的思考方法“明确目标—找到所有完成任务的行动路线—充分利用游戏资源—确定正确路线—获得宝藏”。
思考法则:“铺路策略”就像一个解决问题的思维模型,学生在游戏中不断运用,使其成为思考策略,再逐渐内化,形成良好的思维习惯,在解决问题的过程中螺旋式上升最终形成思维品质,使学生感受到思考的力量。
二、數学实验将抽象概念变成实验数据,感受思考的力量
数学实验化教学一直是数学教师不断探索、创新的教学方式,在科技不断发展的今天,尤其是信息技术课程的引入,使数学实验化教学的实现通过跨学科融合有了新的探索。
以人教版数学教材中“相遇问题”和“追击问题”的教学为例:
(一)与信息课程融合
将全班学生分成10个学习小组,并指定小组长,具体要求:
(1)利用“机器人编程课程”完成“编程机器小车”的搭建。
(2)打开编程软件完成两个小车电机的速率、方向、时间、圈数的设定。先将两个电机功率设置为100的最高转速,方向设置为直行,时间设置为1秒,最后加一个停止。完成后,打开主控器,会看到小车用100的速度向前直行1秒后停止。两个小车调试完以后放在旁边备用。同时准备一个大于2米的皮尺和计时秒表备用。
(二)以数学实验的形式开始“相遇”和“追击”问题的教学
(1)首先教师要求各小组对小车的时速进行数据的测量,A小车在程序上设置30的转速,方向设置为直行,时间为2秒;B小车在程序上设置20的转速,方向设置为直行,时间为2秒。为了保证数据的真实性,两个小车分别测试3次,每次10秒钟,用皮尺测量小车行进的距离,计算得出A小车的平均时速为0.15米/秒,B小车的平均时速为0.1米/秒。
(2)探究相遇问题。
第一步:提出假设问题。
A小车从甲地开往乙地,B小车从乙地开往甲地,它们同时出发,A小车与B小车4秒后相遇,已知A小车的时速为0.15米/秒、B小车的时速为0.1米/秒,甲、乙两地的距离是多少米?
第二步:实验验证。
两个编程车分别放置在甲、乙两地(先任意设定,距离大于1米),然后输入指令让两辆小车相对行驶,4秒后两辆小车同时停止,让学生观察并测量:①两车行驶的距离;②两车相距的距离。
实验结论:减去两车相距的距离,得出两地距离为1米。
再次实验验证:在同一直线上设置甲、乙两地,距离为1米。然后重复上述实验,4秒后两车相遇。
第三步:反思思考——探究数学原理得出相遇问题计算公式。
通过实验,学生得出了以下结论和数据:两辆小车相遇时,行走的距离之和就是两地之间的距离。从而推导出相遇问题公式:速度之和×时间=两地距离。
(3)探究追击问题。
第一步:提出假设问题。
已知A小车的速度为0.15米/秒,B小车的速度为0.1米/秒,B小车从甲地出发,先行4秒后A小车从甲地出发,问几秒后A小车可以追上B小车?
第二步:实验验证。
学生利用秒表计时,得出8秒后A小车追上B小车的实验数据。
第三步:探究数学原理得出追击问题公式。
通过实验学生很直观地看到:A小车追上B小车时,两车行进的距离是不同的。
教师引导学生得出以下实验结论:
①A小车用8秒的时间行驶了B小车“4秒+8秒”的路程。
②B小车先行的4秒路程就是A小车的追击距离,从而推导出公式:追击时间=。
只有所处的学习环境能提供恰如其分的挑战,才能激励学生探索、理解和不断学习。通过信息课与数学课的融合,数学实验改变了数学课堂的教学形式,也改变了学生的学习方式,不仅极大地激发了学生的学习兴趣,还通过跨学科融合,全方位培养了学生的思考力和数学核心素养。
三、主题活动化学习让思考有力量
以“小思考家”思维拓展课程项目“小齿轮”为核心,设计主题活动“小齿轮大世界”。
(一)课前预习
教师布置学生课前查阅有关“齿轮”的文献资料,让学生了解了无论是在工业革命时期,还是在信息技术迅猛发展的今天,小小的齿轮在机械制造、精密仪器、人工智能等高科技领域的基石地位和巨大的技术潜能。
(二)课堂活动
借助齿轮等装置,让学生能够设计、测试机械运行过程并理解其原理。
(1)首先让学生观看齿轮运動的视频。学生直观地看到大小不同的齿数(相互咬合)之间转数的数量关系。
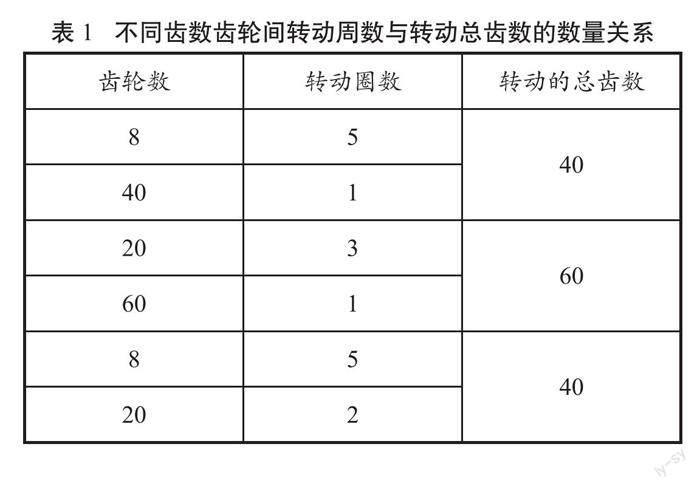
(2)将齿轮学具发给各学习小组:①一个8齿与一个40齿的齿轮组合联动;②一个20齿与一个60齿的齿轮组合联动;③一个8齿与一个20齿的齿轮组合联动。
要求分别在每个齿轮上任意选择一个齿,用彩笔做标记,作为每次转动的起始位置。
(3)要求学生动手操作并统计出下列数据:①每个组合中,大齿轮转1圈,小齿轮转多少圈?②小齿轮转1圈,大齿轮转动了多少个齿?③观察每个齿轮上作为起点标志的齿,转动多少圈能够再次重合?④重合时一共转动了多少齿数?
(4)引导学生列出不同齿数齿轮间的转动所表达的数量关系(见表1):
(5)引导学生探究数据表,得出研究结论:通过统计数据发现每组齿轮两个作为起点的齿重合时,转动的齿数是两个齿轮数的最小公倍数。
(6)活动总结:通过实验初步感受齿轮的工作原理与数学有着密不可分的关系。
无论是游戏化、数学实验化,还是主题活动化教学,其目的都是通过学习方式的改变、教学方法的创新让全体学生主动参与、勤于动手、乐于思考,并感受到数学好玩、数学好用,从而培养学生的学科核心素养和科学探究精神。

