科普教育活动中的计算思维培养方法初探

傅泽禄 方美玉 吴志庆 许玉球 佘协元

摘 要：本文摘用广东科学中心科普教育活动中的案例，探索计算思维的培养方法。案例中结合计算思维六要素展开探讨，展示了计算思维的形成和活动过程，为科普工作者进行计算思维培养提供有益的参考。

关键词：计算思维；科普教育活动；算法

自计算思维概念被提出后，相关理论引起了我国教育界的高度重视。2022年，教育部印发了新修订的《义务教育课程方案和课程标准（2022年版）》，其中《信息科技课程标准》明确将计算思维列为学生必备的四种基本素养之一，鲜明地指出：“信息科技课程要培养的核心素养，主要包括信息意识、计算思维、数字化学习与创新、信息社会责任。这四个方面互相支持、相互渗透、共同促进学生数字素养与技能的提升。”

然而，近十年来有关计算思维培养的研究，研究者主要来自高等教育领域的专家学者、研究生与博士生，虽然也有一线教师注意到了计算思维的培养，但是一线教师研究者的数量并不多［1］。作为实施科教兴国战略和可持续发展战略重要一环的科普教育领域，有关计算思维培养的研究则更为鲜见。

广东科学中心是广东省实施科教兴粤战略和人才强省战略，提高全民科学文化素养的大型综合性科普场馆，积极响应新课标的号召，探索了在科普教育活动中培养学生计算思维的方法。本文以广东科学中心科普教育活动案例為例，为扎根科普一线的科普工作者或教师提供有益的实践参考。

1 计算思维及其培养

计算思维的概念由美国卡内基·梅隆大学计算机科学系主任周以真教授所提出，在该概念被提出之后，世界各国的专家学者陆续跟进研究，从不同角度出发对计算思维的相关概念进行了多样化探讨。与许多新概念一样，计算思维的概念在学术界存在共识，但也有争议。在有关计算思维培养的研究中，郁晓华等对计算思维的培养进行了明确的概念界定，认为计算思维的培养是将计算机科学解决问题的方法和过程扩展到其他学科，进而形成计算化和自动化的解决方案，其核心业务是培养学生如何构建目标问题域和分解任务逻辑，抽象为系统方法并由计算机实现［2］。王飞跃认为，广义的计算思维是一种基于可计算手段并以定量方式进行的思维过程；狭义的计算思维是一种数据驱动的思维过程［3］。

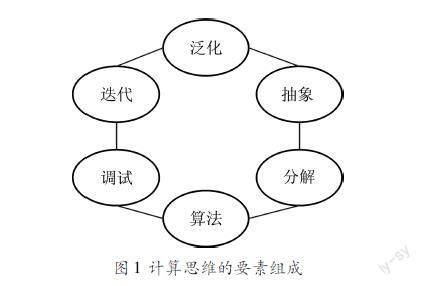
作为共识层面，普遍认可计算思维是一种思维过程，是人的思维，是未来世界认知、思考的常态思维方式，它教会孩子理解并驾驭未来世界。当前，计算思维已被认为是逻辑思维、实证思维后的第三种科学研究的思维方式。一个更具体化的概念是指以计算机软件和硬件设备为工具，通过抽象思维、模型建构、算法组织、自动化管理等操作思维方式，即运用计算机技术来解决问题的思维方式。同时，社会各领域对于计算思维的核心要素也有不同的理解，本文倾向于认同多数研究者认可的六大核心要素（如图1所示），即：迭代、泛化、分解、抽象、算法、调试。

一般地，人们普遍认为科普教育活动中的计算思维培养是指在科普教育活动中，通过计算机软件、程序、编程等方式培养学生的计算思维能力。计算思维培养的方法主要包括编程教育、机器人教育、游戏设计、基于设计的学习活动等。其中，计算机程序设计的过程恰好是解决问题的完整思维过程，因此编程教育被公认为是实施计算思维培养的强有力工具，是表达计算思维的最合适方式。然而，传统的计算机程序设计往往偏重于编程语言和编程技巧和教学，师生们的关注点是掌握一门编程语言和编程方法，并不是以计算思维培养作为课程主要目标，因此如何更有效地培养学生的计算思维，还需要广大教育工作者的不断探索。

2 计算思维培养案例探索

科普教育活动不必拘泥于传统教育的形式，在培养和引导学生计算思维能力方面，可以发挥其手段多样、方法灵活的特点。比如，一方面可以让学生通过模型构建、实验设计、程序攻关、计算机应用等活动，熟练掌握计算机语言、掌握计算机基础知识和技能，形成较强的计算思维能力；另一方面，可以引导学生思考计算机解决问题的步骤和过程，学习通过程序和算法解决实际问题，熟悉相关解决问题的思想和方法，养成解决问题的独立思考能力和动手能力。

我们在编程教学活动中尝试以寻求“算法”作为活动主要目的，通过复杂度逐步递进多个案例，使学生在实践过程中体验计算思维六要素的内在关系和解题路径，取得了良好效果。

计算思维的培养不局限于任何编程语言，学生在活动中可以采用自己熟悉的任何编程语言来实现算法调试。为了便于展示结果，本文重点探索活动中的一个案例，并以python语言进行算法调试。

首先预设生活场景，假设有大小两种重量的水果各100个。现需分配给3个小朋友，在不允许切开水果的前提下，要求每个小朋友拿到的水果重量尽可能地相等。

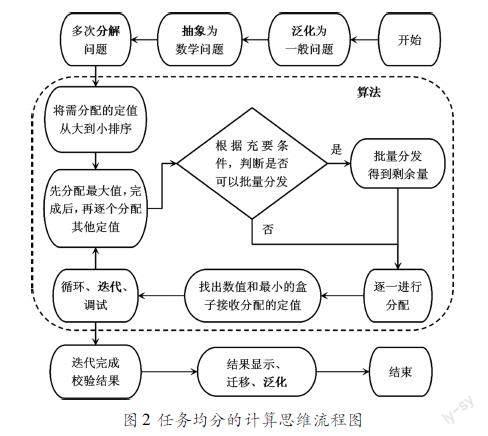
本问题的关键是水果“重量”尽可能地相等，学生的习惯性思维是称重取平均，但由于水果不可以切分，该方法难以保证结果恰好是最优解。教师在活动中适时地引入计算思维，引导学生利用计算思维解决问题，活动过程包括泛化、抽象、分解、迭代、调试等多个环节。例如，将水果问题问题概括并泛化为“任务均分问题”、将问题抽象为“数字分配”问题、将问题分解为多个子问题（如何分配才能保证所得结果是最优解？如何提高分配效率？可以批量分发的充要条件是什么），由子算法综合得到算法，最后进行结果显示和迁移等。任务均分问题计算思维流程如图2所示。

考虑到一般性，均分任务算法中的定值、定值个数、盒子个数均为随机整数，其python代码如下。

import random

import time

boxNum=random.randint（3，11）#盒子个数

ABCnum=random.randint（5，10）#定值个数

abcRange=random.randint（1，101）#每个定值的个数

ABCrange=random.randint（7，31）#定值的大小范围

gg=［（random.randint（1，abcRange），random.randint （1，ABCrange））for i in range（ABCnum）］#生成ABCnum个随机数组

print（f"现有{'，'.join（［f'（{xx［0］}个{xx［1］}）' for xx in gg］）}，需放进{boxNum}个盒子里。"）

Box=［（0，0）for i in range（boxNum）］#Box集合

boxStr=［（0，''）for i in range（boxNum）］#记录并保存分配情况

def LoopsAll（a，A）：#循环迭代，传递参数：a个A

total=0

for xx in Box：

total=total+xx［0］ #已分配的数值之和

gaps=max（Box）［0］*boxNumtotal #盒子中數值总差距

batch=int（（a*Agaps）/（boxNum*A））#根据充要条件计算批发量

if batch<=0：

batch=0

else：

print（"有"，a，"个定值"，A，"，可批量分发，每个盒子分得"，batch，"个。"）

for i in range（boxNum）：

Box［i］=（Box［i］［0］+batch*A，batch）

for i in range（1，a+1batch*boxNum）：

ind=Box.index（min（Box））

Box［ind］=（Box［ind］［0］+A，Box［ind］［1］+1）#逐一分配剩余量

#记录分配情况，将抽象结果显示为具体形式

temStr=''

for i in range（boxNum）：

if Box［i］［1］==1：

temStr=boxStr［i］［1］+'+'+str（A）

else：

if Box［i］［1］>0：

temStr=boxStr［i］［1］+'+'+str（A）+'*'+str（Box［i］［1］）

else：

temStr=boxStr［i］［1］

boxStr［i］=（Box［i］［0］，temStr.lstrip（'+'））

ss=time.time（）#统计时间

gg.sort（key=lambda x：x［1］，reverse=True）#按定值的大小进行排序

for i in range（len（gg））：

LoopsAll（gg［i］［0］，gg［i］［1］）

print（'耗时='，time.time（）ss）

boxStr.sort（）

print（'任务均分结果='）

for i in boxStr：

print（i）

程序运行后，某次随机参数所对应的结果如下：

现有（10个14），（33个26），（9个7），（43个16），（44个25），（12个1），需放进6个盒子里。

有 33 个定值 26，可批量分发，每个盒子分得 5 个。

有 44 个定值 25，可批量分发，每个盒子分得 6 个。

有 43 个定值 16，可批量分发，每个盒子分得 6 个。

有 10 个定值 14，可批量分发，每个盒子分得 1 个。

耗时=0.034515380859375

任务均分结果=

（476，'26*6+25*7+16*7+14+7*2+1*5'）

（477，'26*5+25*8+16*7+14*2+7'）

（477，'26*5+25*8+16*7+14*2+7'）

（477，'26*5+25*8+16*7+14*2+7'）

（477，'26*6+25*6+16*8+14*2+7*2+1'）

（477，'26*6+25*7+16*7+14+7*2+1*6'）

从程序运行结果看，所得结果为最优均分结果之一，此算法具有优秀的运行效率和良好的均分效果。其中，44个定值，批发量为6个，并非7个，这正是最优均分充要条件所决定的。

此案例表明，计算思维六要素是一个相辅相成的整体，各要素之间并无严格的执行次序。计算思维有一定的思维路径，但绝不是单一方向的执行步骤或操作方法，视具体问题的需要，将可能进行多次问题分解，而每次分解均有可能进行再抽象、再调试、再分解。每一个环节都有可能涉及六大要素并且形成该环节的结论，每个结论还可以进一步迁移和泛化。如图2所示，算法是整个流程的核心环节，而寻求算法的过程能天然地结合计算机科学基本思想和基本方法。运用计算思维进行问题求解的过程中，人与计算机各有所侧重，可以粗略地归纳为如下四步路径，其中前三步依赖于人的计算思维，而第四步主要由计算机执行。

路径1：把实际问题泛化并抽象为数学问题，即用数学语言描述问题。

路径2：把数学模型中的变量和条件用特定的符号代替，并形成可计算的规则。

路径3：将问题分解为多个子问题，并通过编程把解决问题的过程写成算法。

路径4：由计算机执行迭代并进行算法调试并显示结果（人们再对结果进行迁移）。

结语

本文探讨了广东科学中心科普教育活动中的实践案例，展现了计算思维的形成和活动过程，归纳了运用计算思维进行问题求解的若干路径。文中案例天然地融入了计算思维六要素，直观地展示了各个要素相辅相成的关系，让学生在实践活动中有路径可循，有方法可以模仿。从活动的效果来看，启发了学生意识，开始主动地利用计算思维去解决问题，其计算思维能力有了明显提高。

诚然，由于计算思维的内涵比较抽象且有较高的理论性，任何培養方法都具有一定的局限性，无疑对教师和学生都提出了更高的要求。如何更有效地培养学生的计算思维，还需要广大教育工作者的不断探索。

参考文献：

［1］常咏梅，李怡灼.计算思维培养的研究综述［J］.甘肃科技，2022，38（12）：4550+58.

［2］郁晓华，肖敏，王美玲.计算思维培养进行时：在K12阶段的实践方法与评价［J］.远程教育杂，2018，36（2）：1828.

［3］王飞跃.面向计算社会的计算素质培养：计算思维与计算文化［J］.工业和信息化教育，2013（6）：48.

基金项目：广东省科技计划项目（科技创新普及领域）2020—2022年广东省创意机器人科普教育创新实践平台建设（项目编号：2021B1414150001）

作者简介：傅泽禄（1976— ），男，汉族，广西岑溪人，硕士，讲师，研究方向：科学普及、科技情报等；方美玉（1983— ），女，汉族，广东揭阳人，本科，经济师，研究方向：科普教育；吴志庆（1983— ），男，汉族，广东顺德人，本科，助理研究员，研究方向：科普推广及科普活动；许玉球（1990— ），男，汉族，广东茂名人，本科，工程师，研究方向：科普教育；佘协元（1974— ），男，汉族，湖南桃源人，硕士，研究方向：科学普及、科技情报、科普标准等。