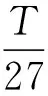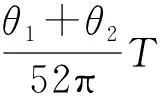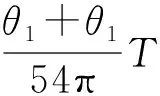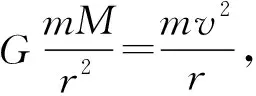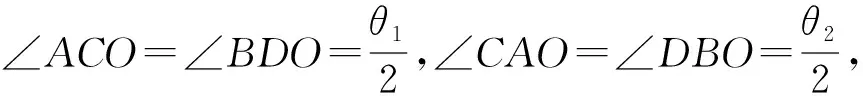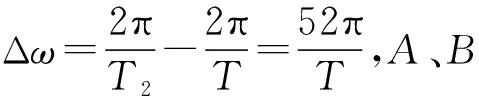天体圆周运动追及相遇问题方法总结和应用
沙希文 詹思楠
(佳木斯市第一中学)
天体圆周运动追及相遇问题来源于圆周运动的追及相遇问题,但是由于天体运动有自己的运动规律,涉及物理知识比较多,包括万有引力定律、开普勒第三定律、圆周运动向心力公式等,所以问题更复杂,但是解题本质上都是相似的,在做这类问题的时候要灵活选择方法和规律。本文分析和总结了解决此类问题的一些方法和在具体问题上的应用。
一、模型的建立和核心素养的培养
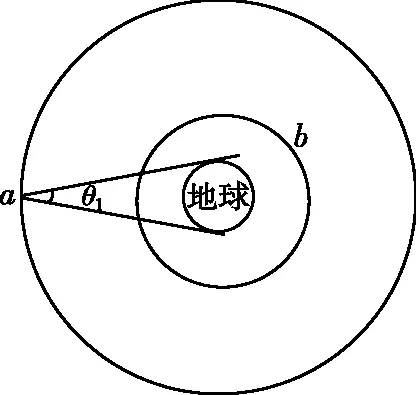
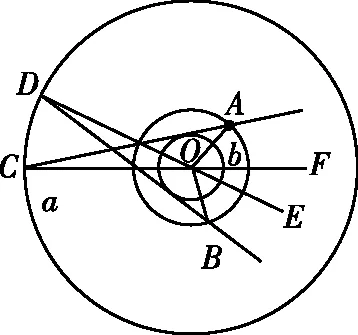
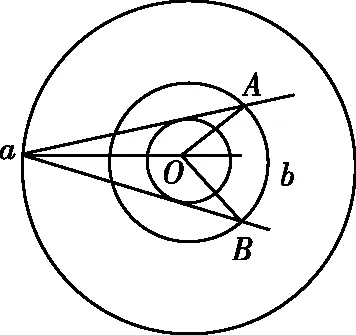
【情景】如图1所示为两个物体绕同一圆心O做同方向的匀速圆周运动,A物体的轨道半径小于B物体的轨道半径,A物体做匀速圆周运动的角速度为ω1,周期为T1,B物体做匀速圆周运动的角速度为ω2,周期为T2,其中角速度ω1>ω2,T1 图1 图2 (1)两个物体相距最近为t=0时刻,则经过多长时间两个物体A、B相距最近? (2)两个物体相距最近为t=0时刻,则经过多长时间两个物体A、B相距最远? 【解析】(1)方法一:角速度法 设经过t时间两个物体相距最近,则 A物体转过的角度为θ1=ω1t B物体转过的角度为θ2=ω2t 要想相距最近,需要满足A比B多转过的角度Δθ=θ1-θ2=2nπ(n=1,2,3,…) 方法二:圈数法 两个物体相遇最近的条件为,A物体比B物体多走圈数 ΔN=N1-N2=n(n=1,2,3,…) 方法三:相对运动法 假设B物体不动,则A相对B转动的角速度为Δω=ω1-ω2 两个物体要是相距最近,则A物体相对B物体转完整的圈数,设时间为t,则满足关系为 Δω·t=2πn(n=1,2,3,…) (2)方法一:角速度法 设经过t时间两个物体相距最远,则 A物体转过的角度为θ1=ω1t B物体转过的角度为θ2=ω2t 要想相距最远,需要满足A比B多转过的角度Δθ=θ1-θ2=(2n+1)π(n=0,1,2,3,…) 方法二:圈数法 两个物体相距最远的条件为,A物体比B物体多走半圈 方法三:相对运动法 假设B物体不动,则A相对B转动的角速度为Δω=ω1-ω2 两个物体要是相距最远,则A物体相对B物体多转半圈的奇数倍,设时间为t,则满足关系为 Δω·t=(2n+1)π(n=0,1,2,3,…) 【拓展知识】如果两个物体绕中心反向运动,从相距最近到再相距最近,方法和上面相同,就是转过的角度或者圈数满足θ1+θ2=2nπ(n=1,2,3,…)的关系。 【知识背景】冲日,简称冲,是由地球上观察天体与太阳的位置相差180°,即天体与太阳在地球两侧,三者共线的天文现象;如果地外行星在地球轨道以外,当太阳把行星和地球分开180°时,简称“合日”,即地外行星和地球在太阳两侧与太阳共线。(来源于网络)下面是以此知识为背景考查天体追及相遇问题的例题。 【例1】(2022年哈三中二模试题)我国火星探测器“祝融号”在2021年9月中旬到10月下旬约一个月的时间内发生短暂“失联”,原因是发生“火星合日”现象,太阳干扰无线电、影响通信。“火星合日”是指当火星和地球分别位于太阳两侧与太阳共线的天文现象,如图3。已知火星公转的周期为T1,地球的公转周期为T2,地球与火星绕太阳做圆周运动的方向相同。结合以上信息,下列说法正确的是( ) 图3 A.火星公转的周期T1小于地球公转的周期T2 B.“祝融号”火星探测器失联过程中火星与太阳连线扫过的面积等于地球与太阳连线扫过的面积 【命题意图】以中国航天事业为背景材料,考查开普勒定律、圆周运动物理量的比较、圆周运动追及相遇问题,问题比较综合,难度中等。 【答案】C 【知识拓展】如果从火星合日变成火星冲日最短需要多长时间? 相遇次数指的是在不同轨道做圆周运动的物体相距最近的时候我们说两个物体相遇一次,相遇一次即运动快的物体比运动慢的物体多走一圈,也就是我们前面分析的问题。 【例2】如图4所示,质点a、b在同一平面内绕质点c沿逆时针方向做匀速圆周运动,它们的周期之比Ta∶Tb=1∶k(k>1,为正整数)。从图示位置开始,在b运动一周的过程中( ) 图4 A.a、b距离最近的次数为k次 B.a、b距离最近的次数为(k+1)次 C.a、b、c共线的次数为2k次 D.a、b、c共线的次数为(2k-2)次 【答案】D 【错因分析】相遇次数指的是同侧相距最近,但要是问的是共线次数,那就包括同侧共线也包括两侧共线。同侧共线为多走整数圈,两侧共线则为二分之一圈数的奇数倍。 【巩固练习】假设有一载人宇宙飞船在距地面高度为4 200 km的赤道上空绕地球做匀速圆周运动,地球半径约为6 400 km,地球同步卫星距地面高为36 000 km,宇宙飞船和一地球同步卫星绕地球同向运动,每当两者相距最近时,宇宙飞船就向同步卫星发射信号,然后再由同步卫星将信号发送到地面接收站,某时刻两者相距最远,从此刻开始,在一昼夜的时间内,接收站共接收到信号的次数为( ) A.4次 B.6次 C.7次 D.8次 【答案】C 卫星传播信号时由于中间天体的遮挡导致信号中断,此类问题和追及相遇问题很相似,唯一不同的是运动快的物体比慢的物体多走的圈数不是整圈数,而是小于一圈或者说角度不到2π,涉及空间的几何关系,比前面讲的例题难度要大一些。 【例3】我国的“天链一号”卫星是地球同步卫星,可为中低轨道卫星提供数据通信,“天链一号”卫星a、赤道平面内的低轨道卫星b,地球的位置关系如图5所示,O为地心,地球相对卫星a、b的张角分别为θ1和θ2(θ2图中未标出),卫星a的轨道半径是b的9倍,且均绕地球同向运行,已知卫星a的周期为T,在运行过程中由于地球的遮挡,卫星b会进入卫星b通信的盲区,卫星间的通信信号视为沿直线传播,信号传输时间可忽略,下列分析正确的是( ) 图5 A.卫星a、b的速度之比为1∶9 【命题意图】同步卫星、低轨卫星信号传播问题,描述天体运动物理量的比较。 【答案】BC 分析CD选项 方法一:如图6所示 图6 方法二:相对运动如图7所示 图7 【方法点评】信号遮挡问题主要是几何关系的分析,方法和圆周运动追及相遇问题相似,其中相对运动的方法表达式比较简洁,但是要变换参考系,思维量大一些,而圈数法或者角度方法空间几何关系比较难分析,两个方法的选择各有利弊,需要根据学生的情况加以选择。 通过几个例题的分析我们可以看出来不同的情境和条件,但是方法都是相似的,都是需要算出两个物体圆周运动转过的角度或者圈数,二者的差值或者和是整数倍或者半周的奇数倍问题,相邻两次就是最小时间值。当涉及空间关系用相对运动变换参考系比较容易理解。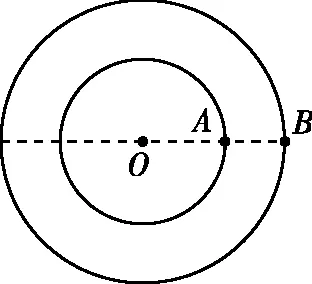

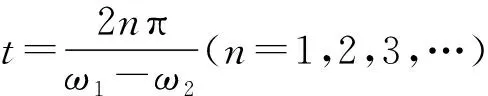
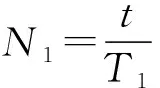
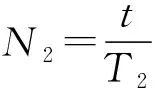
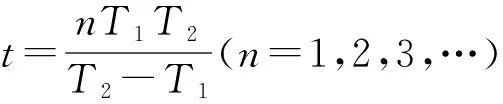
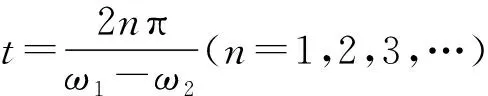
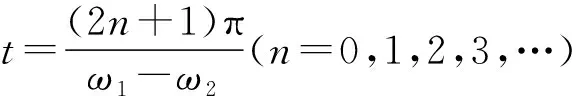
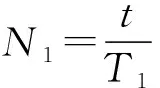
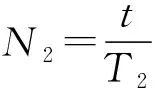
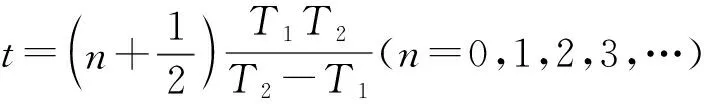
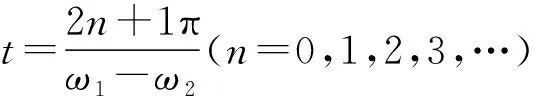
二、解决“视界”问题
(一)“火星合日” “火星冲日”问题分析
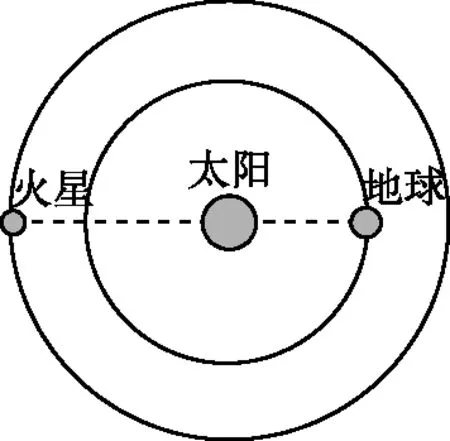
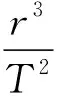
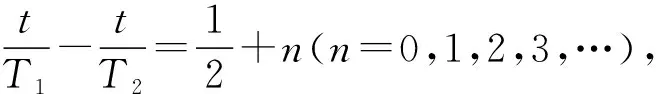
(二)相遇次数的判断
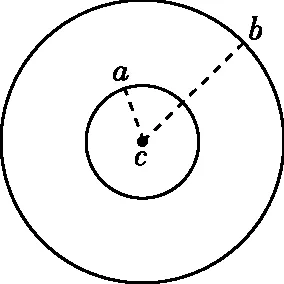
(三)信号传播遮挡问题分析