深层页岩气水平井钻柱动态摩阻扭矩分析*

刘伟吉 冯嘉豪 汪洋 祝效华 李枝林

(1.西南石油大学机电工程学院 2.西南石油大学地热能研究中心 3.中国石油集团川庆钻探工程有限公司)

0 引 言

我国页岩气资源丰富，根据国土资源部发布的资源预测结果显示，我国页岩气总量约为134×1012m3。实现页岩气的经济高效开发，对我国现阶段油气增储上产，确保国家能源安全具有重要战略意义。由于水平井的日均产气量和最终产气量都为垂直井的3～5倍，且效率高，故水平井已成为页岩气开采的主流井型。但在深层页岩气长水平段钻进时，钻柱所受摩阻扭矩大，能量传递效率低，托压问题严重，导致了钻压不能稳定传递，破岩效率大大降低。例如，四川盆地页岩气钻井整体机械钻速仅3～4 m/h，焦页185-3HF井和184-2HF井水平段机械钻速不超过2 m/h，仅为平均水平的25%[1]。因此，针对钻柱所受摩阻扭矩分布及变化规律进行研究，可以有效减轻钻进过程中所产生的托压问题，提高钻井效率。

目前，国内大量学者通过建立钻柱模型对井下接触与摩阻扭矩变化规律展开研究。传统的井下摩阻扭矩模型是C.A.JOHANCSIK等[2]提出的一种在定向井中预测钻柱扭矩和拉力的软绳模型。后来针对软绳模型的局限性，R.G.WHITTEN[3]提出考虑钻柱刚度对摩阻扭矩影响的模型，即刚杆模型，并基于刚杆模型和软杆模型对水平井进行了大量研究。钻柱与井壁的摩阻扭矩计算分静力学分析和动力学分析。静力学分析是针对钻柱变形，通过钻柱静力学模型计算，解决水平井非线性接触问题中接触摩擦力的分布问题[4-5]；同时针对井下不同井段的倾角建立模型，分析钻柱与井壁的接触形态，进而计算摩阻扭矩[6]。动力学分析主要考虑钻柱振动对钻柱摩阻扭矩的影响。文献[7-8]建立了一种可以主动控制纵、横扭振动的钻柱动力学模型，发现钻头运动会引起扭转振动，扭转振动反过来又会激发轴向和横向振动，从而导致钻头弹跳并与井壁发生碰撞，最后基于线性化模型设计了线性二次型调节器(LQR控制器)来消除振荡。许超等[9]针对超长定向复合钻进分别建立了轴向和旋转摩擦力矩模型。LI Z.F.等[10]研究了不同长短轴半径比的减摩接头对钻柱径向振动的影响，进而探究了径向振动对钻柱摩阻扭矩的影响规律。基于振动模型，祝效华等[11]和田家林等[12-13]研究了钻柱动力学模型的完整动态响应，包括接触、摩擦和冲击。胡以宝等[14]利用有限元方法探究了钻速对摩擦振动的影响。祝效华等[15]利用有限元方法建立了大斜度井三维非线性动力学模型和动态扭矩阻力模型，结合全井钻柱系统动力学模型和数值仿真，探究了页岩气水平井的摩阻扭矩、载荷传递和延伸钻进问题。吴泽兵等[16]和LIU J.X.等[17]基于有限元软件建立了钻柱与井眼正交各向异性及非线性接触摩擦模型，探究了钻柱屈曲与钻压之间的关系。张辉等[18]、LI X.M.等[19]和FU J.H.等[20]总结了温度、岩屑床和轴向振动对摩擦因数及井下摩阻扭矩的影响。

经过文献调研，目前国内外对页岩气水平井摩阻扭矩的研究多停留于静态摩阻扭矩，利用有限元建模综合考虑钻柱接触和钻柱振动对动态摩阻扭矩造成影响的文献较少。为此，笔者建立了实钻井眼轨迹的三维全井钻柱系统动力学数值仿真模型，针对深层页岩气水平井摩阻扭矩大的问题，以W202H11-1井的钻井数据为基础，分析了钻进过程中钻柱系统摩阻扭矩、应力分布及振动情况，以期为深层页岩气水平井钻井参数优化及提速方案设计提供依据。

1 钻柱动态摩阻扭矩分析

1.1 动力学模型理论

在钻井过程中，钻柱的多变和不可预测性给动力学计算带来了问题，必须通过全井动力学模型进行分析。全井动力学模型是假设全井钻柱系统为弹簧-质量-阻尼系统，利用Hamilton原理和有限元方法，通过假设整个钻柱由多个细小单元体离散而成，将每个钻柱单元与井壁考虑为随机碰撞和摩擦，通过虚功原理得到第e个钻柱单元的平衡方程：

(1)

(2)

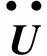
上述全井非线性动力学模型可以适配井下钻柱的非线性接触和几何问题，包括钻柱的弯曲、扭转及纵横扭耦合振动问题等。引入边界条件和载荷后，采用逐步积分中的Wilson-θ法求解式(2)，即可完成对整个钻柱系统的动力学特性分析。为了计算钻柱摩阻扭矩，将细小钻柱单元作为研究对象，其受力如图1所示[21]。

图1 钻柱单元受力图

(3)

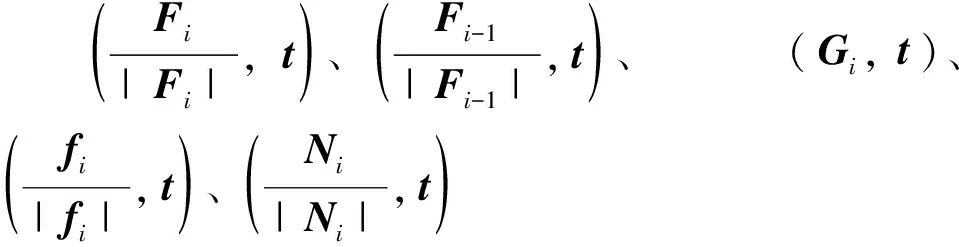
计算时，若钻柱向下延伸则fi取负，钻柱上提则fi取正。同时，钻柱与井壁的接触通常分高边接触和低边接触。若钻柱振动接触井壁时，高边接触则Ni取负，低边接触则Ni取正。因为钻柱与井壁的接触为随机接触，而非连续接触，则若未接触时，fi和Ni皆取0。

由逻辑弹簧阻尼系统可以求得钻柱节点与井壁碰撞后的接触力：

Ni=kα+cvri

(4)

式中：k为岩石和钻柱之间的刚度系数，N/m；α为钻柱向井壁的趋近距离，m；c为岩石和钻柱之间的阻力系数，(N·s)/m；vri为单元处切向速度，m/s。

若节点处受力满足式(3)，则可以直接求出该点处的摩擦力及摩擦扭矩。

1.2 全井钻柱系统摩租扭矩数值仿真模型

本文以W202H11-1井为算例进行模拟仿真。钻柱在井下作业时，随着轴向力和扭矩的传递，自身也会发生扭转变形而弯曲，与井壁接触，利用Abaqus软件对全井进行建模仿真。整个模型包括井壁、钻柱、PDC钻头和岩石4大模块。在建模前需要对模型做如下假设：①钻柱在接触过程中处于线弹性状态；②钻柱初始轴线与井眼中心轴线相重合；③井壁为刚体。

本井采用“直-增-稳-降-增-水平段”井眼轨迹剖面。根据录井参数建立全井数值模型，井眼轨迹参数检测表如表1所示。

表1 井眼轨迹参数检测表

该井四开采用的钻头为五刃PDC钻头，外径215.9 mm，长0.3 m。全井采用的主要钻具组合为：ø127.0 mm斜坡钻杆×2 273 m+ø127.0 mm加重钻杆×54 m+ø165.0 mm随钻震击器×3.7 m+ø127.0 mm斜坡加重钻杆×135 m+ø165.0 mm旁通阀×0.5 m+ø127.0 mm斜坡钻杆×1 700 m+ø165.0 mm止回阀×0.5 m+旋转导向系统×17 m。井壁直径240 mm，长4 184 m。岩石参数以龙马溪组层位为标准，全井钻具和岩石性能参数如下：岩石泊松比0.201，弹性模量23 GPa；钻柱泊松比0.300，弹性模量210 GPa；密度7 820 kg/m3，阻尼系数1.56×106(N·s)/m，刚度系数6.57×1011N/m；钻井液密度2.1 g/cm3。将PDC钻头、井壁、钻柱和岩石装配后得到全井有限元模型，如图2所示，同时还展示了模型下端装配剖面。

图2 全井段井下钻具组合模型及部分剖面图

基于上文水平井全井动力学模型，根据W202H11-1井实钻参数，对钻柱、井壁、PDC钻头及岩石施加相应的载荷和边界条件。在分析步中，设置时间总长度为6 s，在均匀时间情况下进行输出，并根据实际井下工况为钻柱施加浮重和扭矩，最后对各部件自由度创建约束，计算钻柱与井壁的接触力、接触力矩、钻柱系统的应力分布、振动以及轴向力的传递情况。

1.3 模型验证

为了验证所使用的钻柱摩阻扭矩模型的正确性，本文利用该模型计算得到的3 500～4 184 m井段大钩载荷与实际钻探中测得大钩载荷相对比，结果如图3所示。

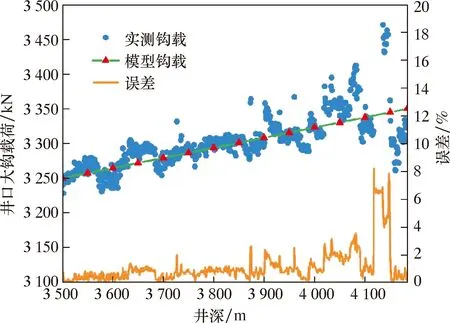
图3 3 500～4 184 m井段大钩载荷对比曲线

由图3可以发现，实测大钩载荷随井深的不断增加而增加，大钩载荷均值增加了94 kN。利用钻柱摩阻扭矩模型计算所得的大钩载荷，同样随井深增加而增加，且大钩载荷均值增加了86 kN，二者的误差介于0～8%之间，平均误差只有1.45%，故利用该模型计算的摩阻扭矩具有良好的适用性。

2 结果分析与讨论

2.1 下部钻具位移特性

钻头所受到的钻压由轴向力传递，主要受到顶驱拉力和钻柱浮重的影响。图4为顶驱拉力和钻压动态曲线。由图4可以看出：在2 s左右井口所受轴向力趋于稳定，且保持在327 kN上下小幅度波动；钻头处轴向力在稳定后，钻压在68 kN左右波动，且波动幅度较明显，极大值达88 kN，极小值为29 kN。较大的钻压波动可能会导致跳钻和反钻现象，并且显著缩短钻头的使用寿命。

图4 顶驱拉力和钻压动态曲线

钻头与岩石接触导致振动，振动可能会导致模型失效，故利用X、Y、Z轴三向加速度来反映钻头与钻柱耦合处振动情况，X为轴向，Y、Z为横向。图5为钻头加速度曲线。由图5可得：钻头轴向加速度峰值69 m/s2，大多数情况在20 m/s2以内波动；横向加速度峰值207 m/s2，大多数情况在100 m/s2以内波动。由此可知，此刻钻头振动并不剧烈，为下文计算接触力和摩阻扭矩提供了可靠性。

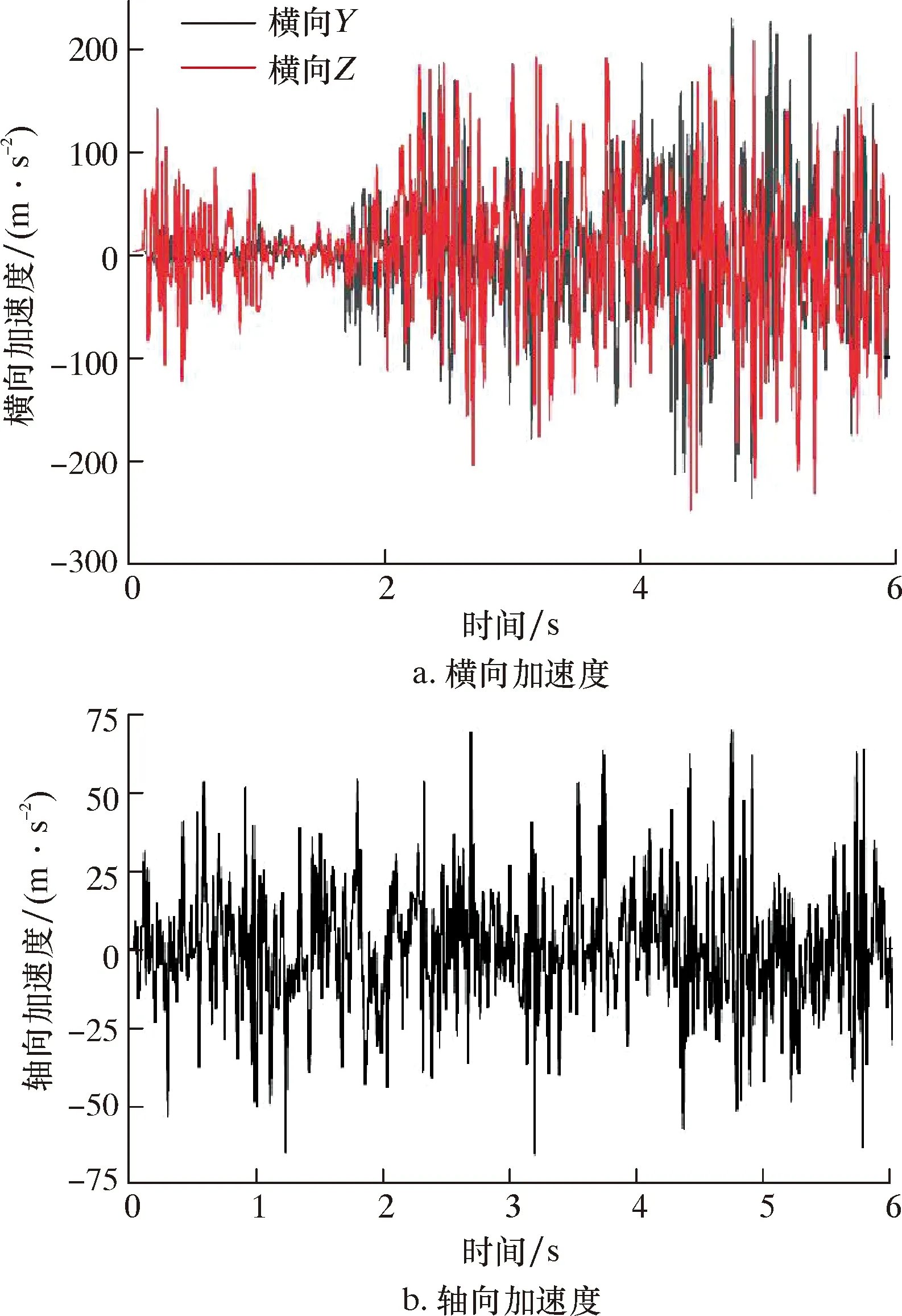
图5 钻头加速度曲线

2.2 动态摩阻扭矩分析

为了对钻柱的摩阻扭矩进行分析，首先需要对钻柱与井壁的接触情况做出讨论，利用ABAQUS软件对钻柱所受到的接触力进行计算。图6为钻柱进入稳定钻进状态后3～5 s时的接触力及平均接触力变化情况。图7为各井段的接触力分布云图。

图6 全井段钻柱接触力

图7 各井段的接触力分布云图

由图6可以看出，随着钻进的不断延续，钻柱所受接触力的变化幅度较小，在一定范围内波动，并且除了增斜段钻柱与井壁连续接触外，各井段钻柱与井壁的接触皆为间歇性接触。调整段钻柱平均接触力为0.2 kN，但随着方位角变化，钻柱弯曲导致与井壁接触力激增。增斜段接触力峰值达10 kN，平均接触力3 kN，变化幅度超过70%。水平段钻柱接触力减小后稳定，均值为0.8 kN。

图8为全井段钻柱所受瞬态应力及接触力云图。由图8可以看出，钻柱所受应力的变化趋势与接触力变化相同，在增斜段处应力值最大，约为123 MPa。同时可以发现在直井段和调整段的接触力方向不一致，而增斜段和水平段的接触力几乎朝向同一方向，说明在弯曲段之前钻柱沿井眼轴线来回波动，而进入弯段后钻柱几乎都与下端井壁接触。

图8 全井段钻柱所受应力及接触力分布图

基于接触力可以对全井的摩阻扭矩进行计算分析。图9为全井段钻柱平均摩阻扭矩和累计摩阻扭矩曲线。分析可知，整个钻柱所受到的平均摩阻扭矩与上文接触力分布趋势相同，井深300 m内的直井段几乎没有与井壁接触。在进入弯曲段之前，钻柱的摩阻扭矩都较小，直到造斜开始后，钻柱与井壁下端稳定接触，摩阻扭矩激增，随后水平段的摩阻扭矩趋于稳定。将平均摩阻扭矩累加后可以发现，全井摩阻扭矩达19.5 kN·m。

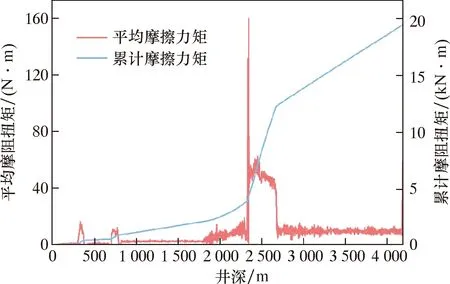
图9 全井段钻柱平均摩阻扭矩和累计摩阻扭矩曲线

2.3 钻井参数对动态摩阻扭矩的影响

钻压和钻速对动态摩阻扭矩的影响曲线如图10所示。由图10可知，随着钻压的增大，钻柱所受的摩阻扭矩有明显的增大。钻压为60 kN时，全井摩阻扭矩为19.5 kN·m；而钻压增大至140 kN后，摩阻扭矩增大至28 kN·m。由此可知，在为钻头施加钻压时，应在满足钻进速度的前提下尽可能地减小钻压，从而减小摩阻扭矩，提高钻井效率。同时由图10还可发现，随着钻压增大至140 kN，未发生下部钻具屈曲卡死现象。图11为不含钻头的水平段钻柱(4 100～4 184 m)弯曲状态。设置变形缩放系数为20，以便于观察。由图11可以看出，随着钻压增大，钻柱弯曲幅度增加，且越远离钻头处的钻柱越偏离井眼轴线。

图10 钻压与转速对动态摩阻扭矩的影响曲线

图11 下端水平段钻柱(4 000～4 184 m)弯曲状况(弯曲位移)

钻柱与井壁的摩擦为滑动摩擦，而顶驱钻速(转速)决定了钻柱与井壁接触摩擦相对速度的大小，故有必要探究顶驱转速与摩阻扭矩的关系。由图10b可得，随着转速从5 rad/s增加至10 rad/s，摩阻扭矩从22.8 kN·m减小至16.0 kN·m，变化幅值为30%。由此可知，增加转盘转速有利于减小钻柱的摩阻扭矩，但设置过高钻速会导致模型失效。

3 结 论

(1)钻柱所受平均摩阻扭矩在增斜段处激增达到极大值，而进入水平段后，摩阻扭矩急剧减小，最后趋于稳定。水平段的平均摩阻扭矩略大于调整段，且摩阻扭矩的数值分布趋势与接触力、钻柱所受应力的分布趋势相同。

(2)随着顶驱转速的升高，钻柱全井段所受摩阻扭矩显著减小；随着钻压的增大，钻柱全井段所受摩阻扭矩显著增大。

(3)钻柱所受的摩阻扭矩除了增斜段是连续分布的以外，水平段和调整段都是间歇性分布，但水平段比调整段分布更密集。同时钻柱接触力在水平段和增斜段都为低边接触。

(4)每当钻柱因井斜角、方位角变化而弯曲时，其所受应力、接触力和摩阻扭矩都会有明显的增加，且增加的快慢与钻柱的弯曲程度呈正相关。经过对钻柱接触力峰值和摩阻扭矩峰值的研究，增斜段处钻柱由于波动幅度大、极值大，更容易发生疲劳，应重点关注。