基于联合对抗深度迁移的轴承故障诊断方法*

陈纤 邹龙庆 李明磊 唐友福 缪皓 韩吉程

(1.东北石油大学机械科学与工程学院 2.中国石油天然气集团有限公司工程和物装管理部 3.大庆钻探工程公司)

0 引 言

滚动轴承作为旋转机械中的重要承载部件，通常工作在高速、重载、高温、腐蚀的复杂恶劣工况下，容易产生磨损、剥落、断裂等故障，轻则导致设备加工偏离有效指标，造成噪音污染、影响生产进度及产品质量，重则导致设备损坏，造成重大的经济损失。因此，开展有效的滚动轴承状态监测与故障诊断研究具有重要意义[1-2]。

目前广泛应用的深度学习算法在大数据分类和预测上具有明显优势。但是由于长期积累的滚动轴承现场监测信号往往是以未标记的正常样本为主的大数据，故障样本较少而且受噪声及监测误差的影响，有用故障信息容易淹没在正常样本数据中，特别在变工况和不同场景下，数据集服从不同分布，难以训练出鲁棒性好的诊断模型。因此，有必要研究一种基于少量标签样本建立的可靠诊断模型，对目标域数据进行分类识别。据此引入迁移学习的概念，它是一种半监督的学习算法，能够实现不同领域或任务之间的知识转化。但迁移学习对数据的特征表达能力不如深度学习，所建模型无法有效反映滚动轴承故障状态的现实情况。为此，如何将深度学习和迁移学习进行有机融合，建立互补的诊断模型是目前国内外学者广泛深入研究的热点。YANG B.等[3]提出一种基于特征的迁移神经网络，借助多层域自适应和伪标签学习减小源域与目标域之间的特征差异，能用海量未标注数据有效诊断滚动轴承故障。LI X.等[4]提出利用多核最大均值差异法构造一种多层域自适应卷积网络，将源域中学习到的表示适配到目标域中应用，并准确预测不同电机负载下的滚动轴承故障等级。陈祝云等[5]提出一种增强迁移卷积神经网络来改进机械设备在变工况下的诊断精度和泛化能力。孙灿飞等[6]提出了结合域对抗与深度编码网络的自适应域对抗深度迁移故障诊断方法，解决轴承故障诊断在变负载以及强噪声下的诊断难题。WU Z.H.等[7-8]提出一种利用长短期记忆网络进行轴承故障诊断的迁移学习方法，通过联合分布自适应来减小源域数据集和目标域数据集之间的概率分布差异，该方法对噪声具有很强的鲁棒性，并且在不同的噪声水平下具有出色的性能。WANG X.等[9]通过优化残差网络构建多尺度特征学习器，缩短2个域之间的条件分布距离，该模型可以从2个域中提取判别性和强大的特征，避免信息的丢失。ZHAO Z.B.等[10]提出一种联合分布领域对抗网络模型，并应用于凯斯西储大学滚动轴承故障的诊断。LIU J.等[11]提出一种自注意力小样本迁移学习模型，以较小的训练样本实现更高的准确性，该方法不能实现端到端训练。LI Q.F.等[12]结合知识图谱，提出了一种基于对抗网络的轴承故障诊断迁移学习方法，结果表明所提方法证明了理想的泛化能力，但其分类识别准确率有待提高。CHEN P.等[13]提出一种联合切片Wasserstein距离的无监督域自适应，以提供端到端训练和更高的精度。

以上方法虽然取得一定的诊断效果，但是由于未能同时考虑减少不同数据边缘分布距离和条件分布距离，模型可迁移、泛化能力以及识别的准确率未能达到理想效果。为此，笔者提出一种深度迁移学习算法——联合对抗深度迁移方法，并将其应用于滚动轴承的故障诊断。该方法能够有效实现现场滚动轴承大数据小样本的诊断识别，自适应和泛化能力较强，可为设备的预知性智能维护与健康管理提供有力支持。

1 联合对抗深度迁移模型的原理及建模过程

1.1 原理

假设在实验室设备中获得的数据或真实场景上带有标签的数据被记作有标记的源域(data obtained in laboratory equipment，DLE)，而由其他实验室设备或真实场景测量的未标记数据被用作目标域(data in the real-case scenarios，DRS)，显然2个域具有不同的特征分布。受对抗网络的启发，提出一种联合对抗深度迁移模型，其总体框架如图1所示，主要包括特征生成器、联合特征、领域判别器和分类器。其中，特征生成器由具有批量归一化层的卷积神经网络来实现，以提取域不变特征，加速训练过程和提高网络泛化性能，并更好地保留每个域的不同特征分布。联合特征结构是利用前K个相关标签生成DRS的标签，以此计算数据条件分布，提高标签的预测精度，动态域对齐用于平衡边缘分布和条件分布，以提高模型的可迁移能力，再利用联合广义切片Wasserstein距离准则计算联合分布，以减少计算量和提高模型的训练速度。域判别器用于区分不同的域以进行更全面的域适应，这形成了对抗性的域损失函数。分类器用于预测最终标签。

1.2 建模过程

(1)特征生成。特征生成器由一个4层卷积网络组成，输入大小为1×1 024的一维振动信号，经过第一层卷积核大小为15×1的卷积层，输出的信号大小为16×1 010。第二、三、四层的卷积核大小都设置为3×1，最终全连接层的输出大小为256。卷积神经网络的层数及大小设置如表1所示。

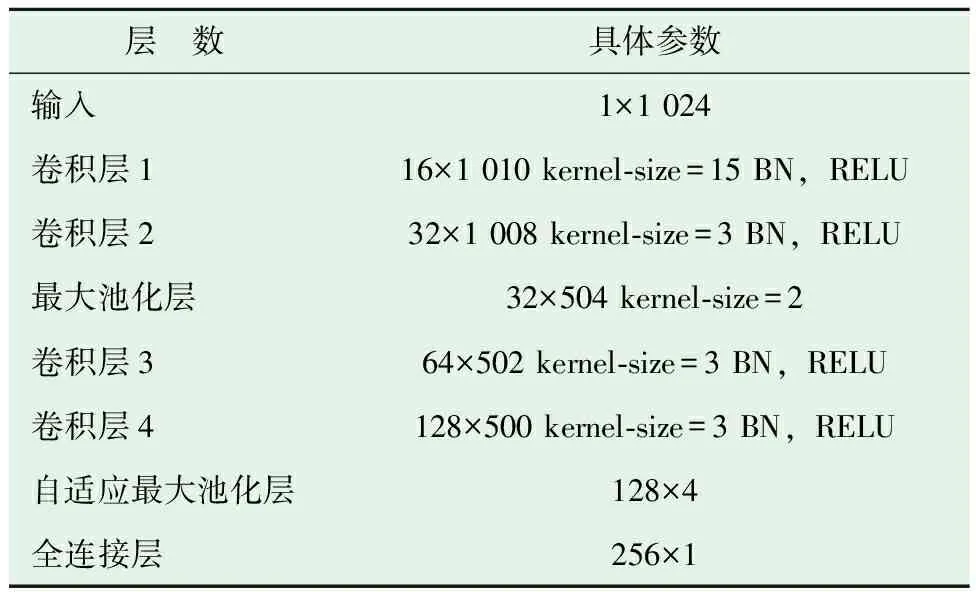
表1 卷积网络参数

(1)

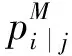
假设有5个有着相似特征的样本，经分类器预测后有的标签值ypred存在错误，为降低发生错误的概率将这5个样本按相似性从大到小排列。若K=3，即选择前3个最相似样本对应的预测，最后选择出现频率最高的标签值作为最终待测样本标签值，记作M(yK)。该方法可以明显降低对目标域标签值预测的错误率并且能准确计算特征条件分布。目标域标签损失可以写成：

(2)

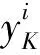
为实现特征条件分布更精准的度量，本文提出广义切片Wasserstein距离，该距离基于原始Wasserstein距离演变而来。传统Wasserstein距离存在难以测量高维分布的瓶颈，目前研究学者提出许多方法来改善Wasserstein距离的计算，例如切片Wasserstein距离[14]，其通过线性分片与拉东变换相关的概率分布来计算。虽然切片Wasserstein距离需要较少的计算复杂度，但是随机选择的线性投影的数量非常大，并且不能保证所选择的线性投影将提供特征分布距离的有效评估。受广义拉东变换的启发，通过将概率测度的线性切片扩展到非线性切片，提出一种新的测度距离——广义切片Wasserstein距离。

广义拉东变换由经典拉东变换发展而来。经典拉东变换是将超平面上的积分推广到流形超曲面上的积分，其定义如下：

(3)

式中：RPS/T表示在超平面Rd上将高维分布投影到低维分布上的无穷积分集；PS/T表示源域和目标域的概率分布函数。Sd-1表示超平面Rd-1中的单位球面，∀w∈Sd-1，∀t∈R，δ()表示一维狄拉克函数。广义拉东变换可表示为：

(4)

当g(x，w)=〈x，w〉时，经典拉东变换是广义拉东变换的特例。进一步地，广义切片Wasserstein距离表达式可定义为：

GSW(PS，PT)=

(5)

式中：PS、PT(PS/T)分别表示源域和目标域的概率分布函数。

利用该广义切片Wasserstein距离度量训练样本和测试样本特征概率分布距离，首先计算源域和目标域之间的联合分布差异。联合分布由边际分布和条件分布组成，2个域之间的边缘分布差异Dmar表达式为：

Dmar=GSW(PS，PT)

(6)

本文采用前K个相关标签来标记目标域数据，2个域之间的条件分布差异Dcon表达式为：

(7)

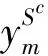
因此，上述的联合分布可以定义为：

Dj=Dmar+Dcon=GSW(PS，PT)+

(8)

以往的许多方法只分别考虑了边缘分布对齐和条件分布对齐，或者将边缘分布和条件分布以一种比重相同的方式对齐，没有考虑到这2种方式在实际应用中的重要性可能不同，从而产生了2个不同领域之间的传递迁移能力下降的问题。针对上述问题，本文通过一个平衡因子的计算动态对齐边际分布和条件分布，该平衡因子μ∈[0，1]。动态域对齐的表达式为：

(9)

2 联合对抗深度迁移学习在滚动轴承的应用

2.1 试验数据

为了评估所提出的方法在机械故障诊断领域中的可迁移能力，将其应用于不同数据集进行试验验证，2个标准数据集具体见表2和表3。现场轴承数据是从现场实际工作的往复压缩机上采集得到，其负载和运行条件不断发生变化，故障类别通常为疲劳、点蚀、塑性变形等，具体可见表4。

表2 凯斯西储大学轴承数据(CWRU)

表3 西安交通大学轴承数据(XJTU-SY)

表4 现场实际轴承数据

表2中：IF为滚动轴承内圈故障；RF为滚动轴承滚动体故障；OF为滚动轴承外圈故障。

表3中：CF为滚动轴承保持架故障。

2.2 模型训练过程

Lc(Fc(Fg(xs))，ys)=

(10)

域判别器学习函数Fd对输入数据进行域分类，域判别器的损失函数可表示为：

Ld[Fg(xs)，Fg(xt)]=

(11)

最后，应用上文提出的动态分布域对齐来平衡特征边缘分布和条件分布，以提高模型的泛化能力，域对齐损失表示如下：

+λ[μDmar+(1-μ)Dcon]

(12)

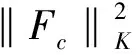
图2 计算流程图

文中提出模型的整体目标函数表示如下：

L=Lc+LK+Ld+LDA

(13)

2.3 结果与讨论

选择凯斯西储大学数据集和西安交通大学数据集作为DLE，不同工况下的迁移任务和从DLE到DRS的迁移任务如表5、表6和表7所示。将本文提出方法与原始卷积(S-only)、多核最大平均差异度量[15](multikernel maximum mean discrepancy，MK-MMD)、领域对抗神经网络[16](domain adversarial neural network，DANN)、特征对齐[17](correlation alignment，CORAL)和联合最大平均差异[18](joint maximum mean discrepancy，JMMD)等进行比较。

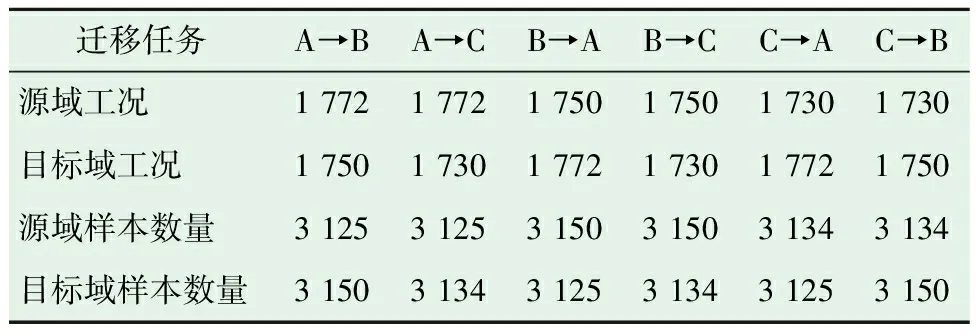
表5 基于凯斯西储大学轴承数据迁移任务

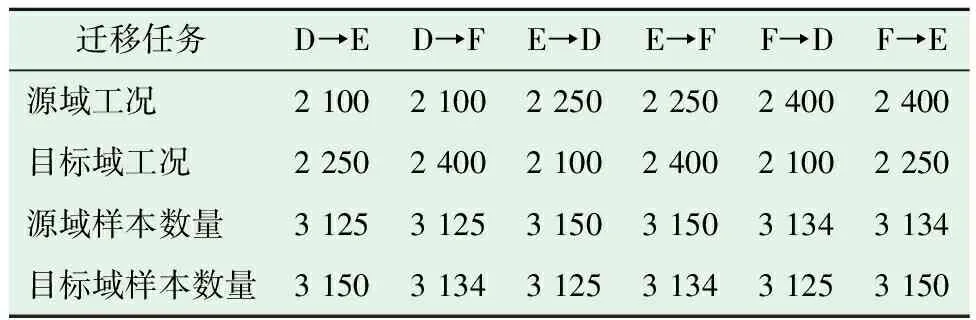
表6 基于西安交通大学轴承数据迁移任务

表7 DLE到DRS的迁移任务

不同工作条件迁移结果如图3～图5所示。显然，本文提出的JGSWD方法在6个任务上优于其他比较方法。其中S-only的准确率最低，JGSWD作为域自适应对抗方法，取得了比DANN更好的性能。随机选择B→C和E→F迁移学习任务作为t-SNE可视化的对象，它们的特征可视化结果如图6和图7所示。在图6和图7中，10种颜色代表10个类别，圆形点代表源域，相反，叉点代表目标域。对比其他方法，JGSWD方法的可视化结果图能够较好将圆形和十字形点聚集在一起，使源域和目标域的特征分布更加一致，且10种颜色分类更加清晰明朗，该方法实现了更好的聚类。

图3 凯斯西储大学轴承数据A→B迁移分类预测准确率

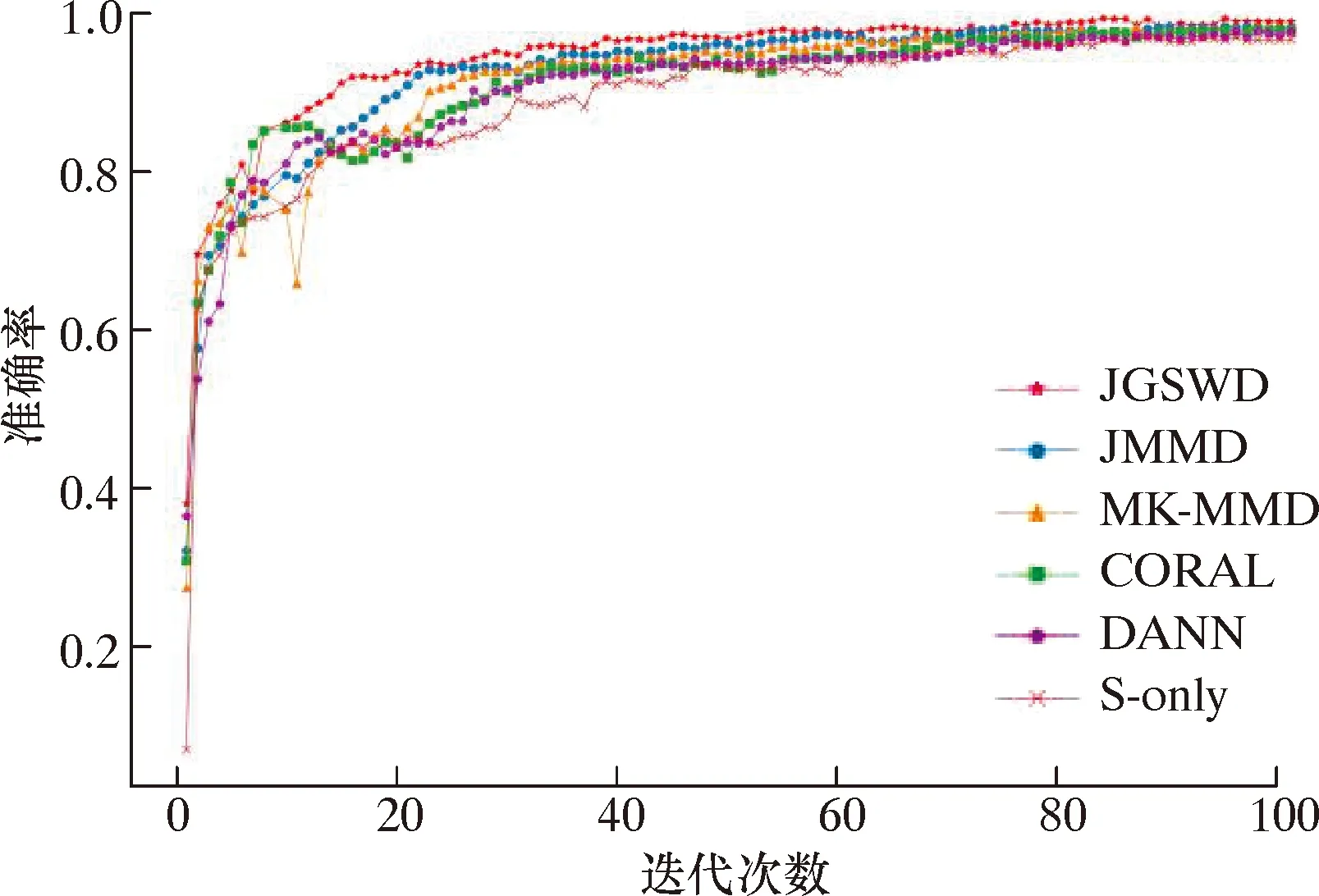
图4 西安交通大学轴承数据D→E迁移分类预测准确率

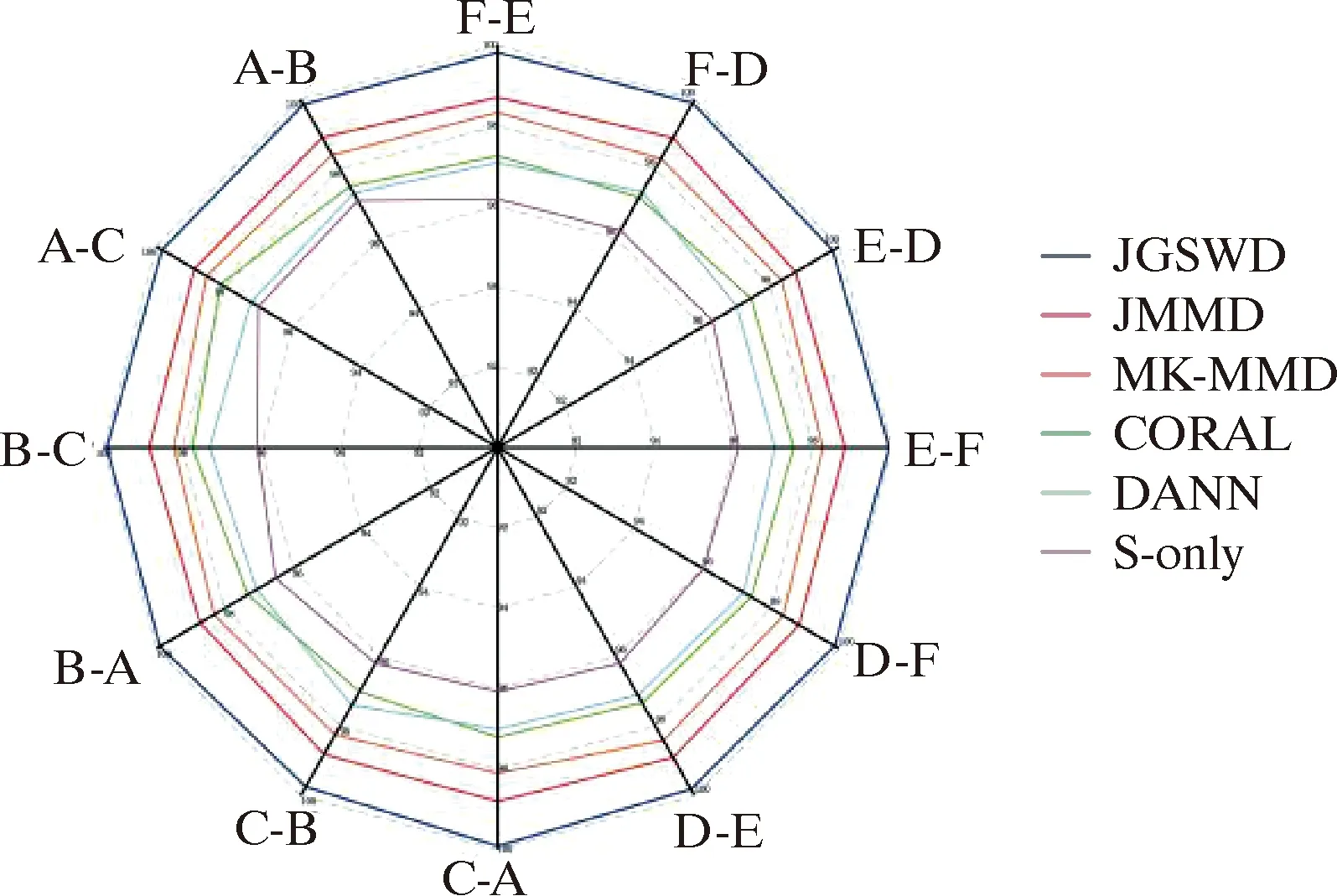
图5 轴承分类预测准确率雷达图

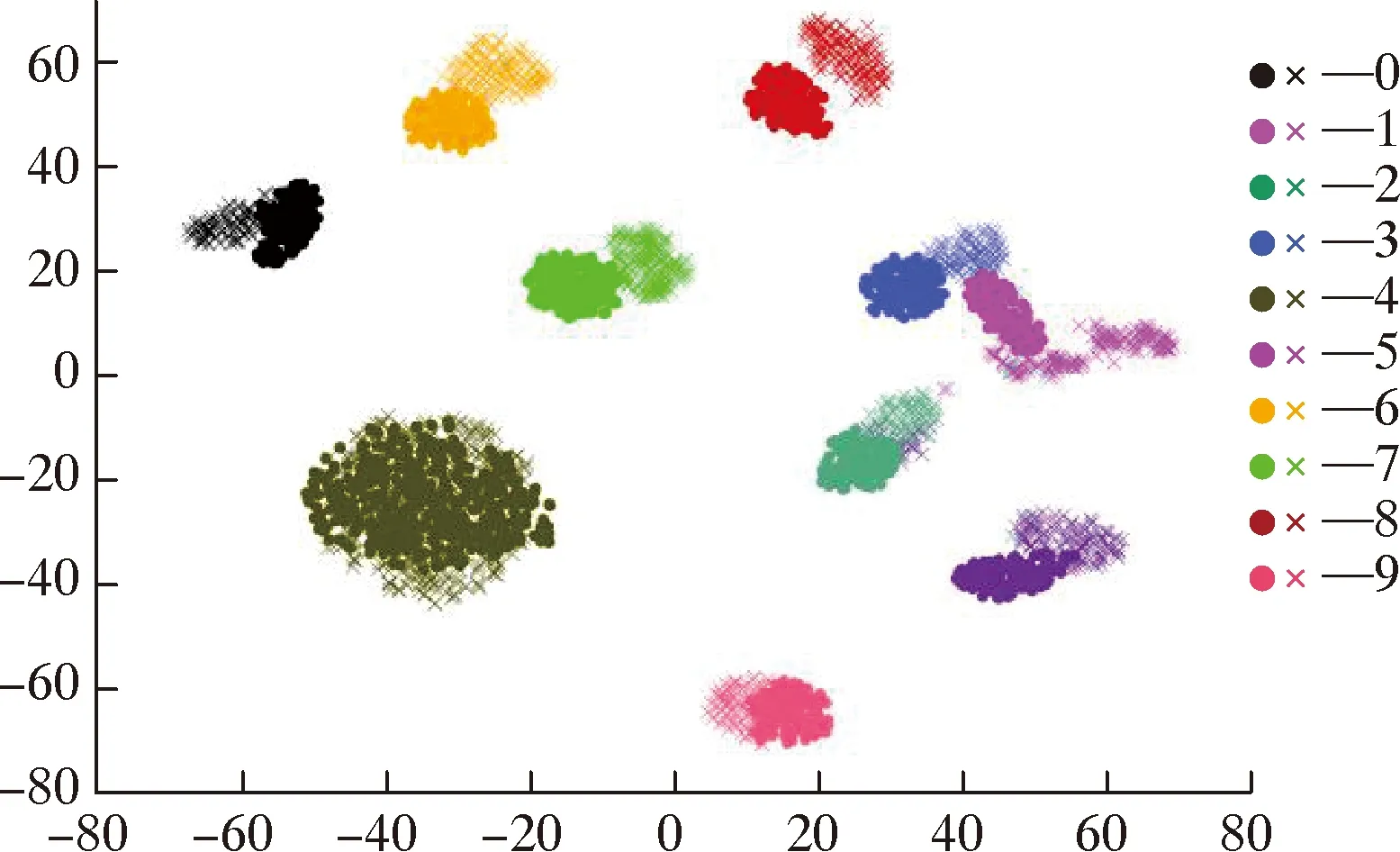
图6 B→C迁移任务的可视化

图7 E→F迁移任务的可视化

DLE到DRS的迁移结果表明：该试验的挑战在于故障轴承数据是在不同的机械设备中获得的，并且目标域是未标记的数据，导致DLE和DRS的分布差异更大。试验中本文所提出的方法分类性能如图8～图10所示，分类准确率高达97%，具有很好的特征可视化性能，并且预测测试样本故障类型的时间大大减少。

图8 CWRU→DRS的迁移任务分类预测准确率

图9 XJTU-SY→DRS的迁移任务分类预测准确率

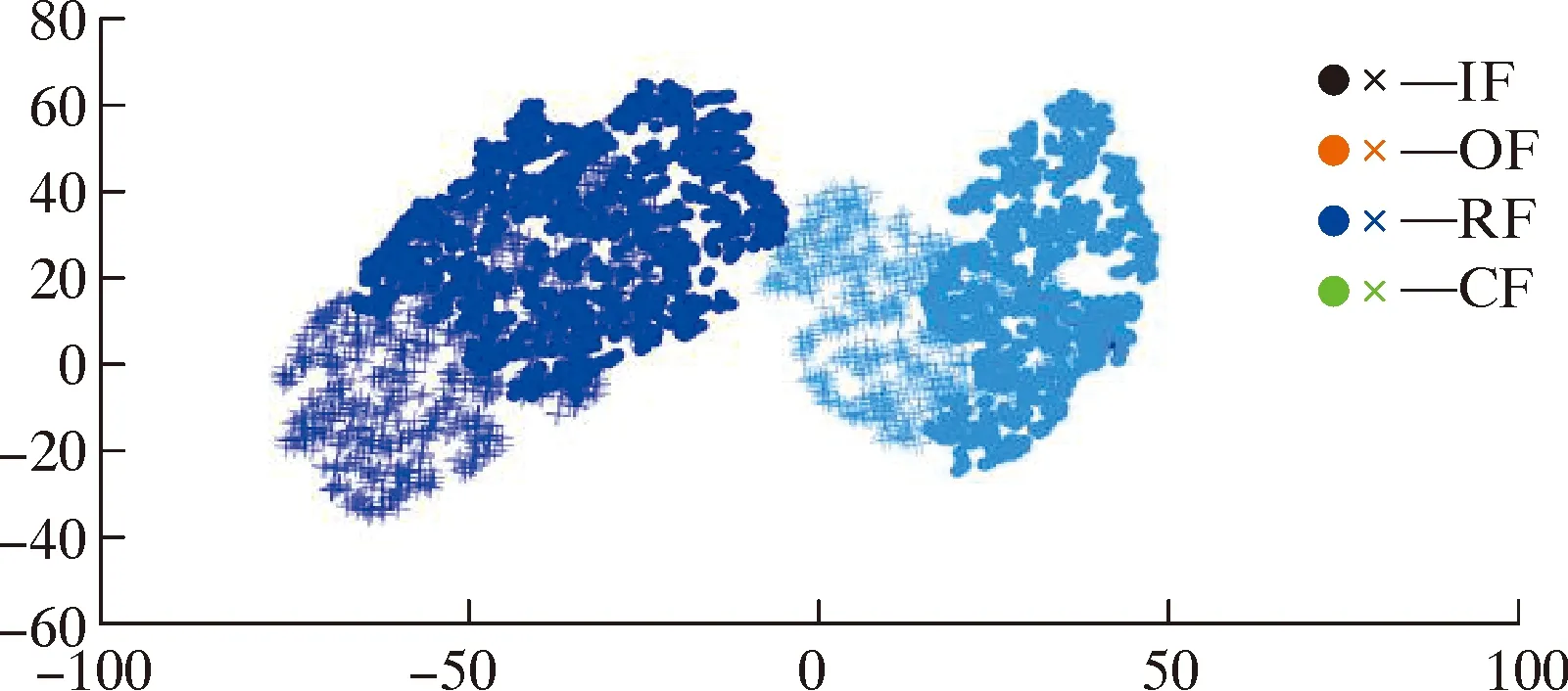
图10 DLE到DRS迁移任务的可视化

为了更好地证明每一项创新点在分类准确性上的有效性，对其进行消融试验。G：广义切片Wasserstein距离；K：前K个相关标签；DA：动态域对齐。“JGSWD-G/DA/K”表示没有广义切片Wasserstein距离、前K个相关标签和动态域对齐的故障诊断模型。消融试验如图11所示。很明显，本文所提出的JGSWD方法每一个创新点都有效地提高了模型迁移泛化性能和分类预测的准确性。

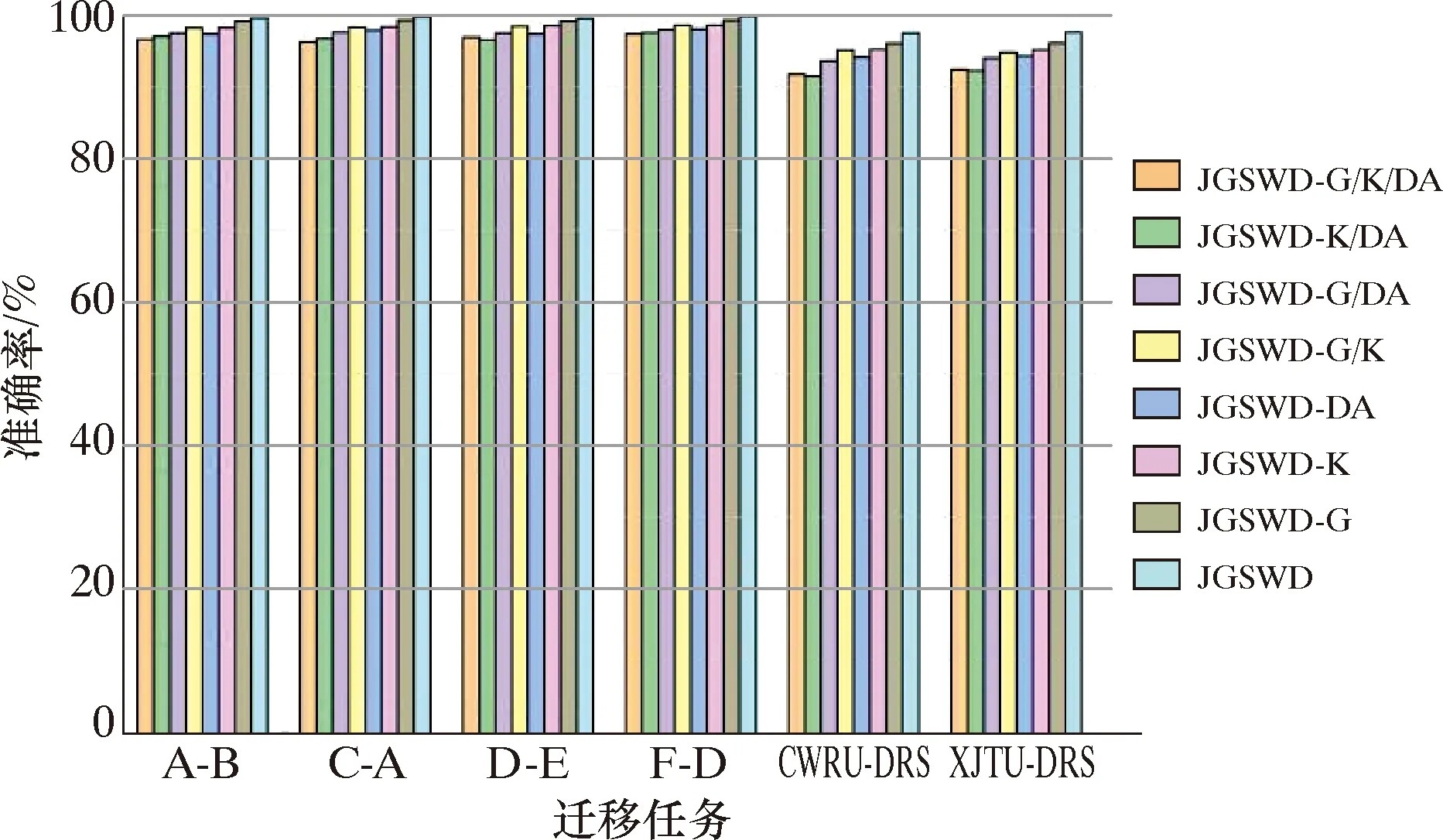
图11 消融试验

4 结束语

本文提出了一种基于领域自适应的滚动轴承故障诊断联合对抗深度迁移学习方法，主要解决DRS和DLE联合特征分布不同的问题，并通过动态平衡边缘分布和条件分布来最小化2个领域之间的联合差异，采用广义切片Wasserstein距离，极大减少了复杂计算量，提高了故障诊断的速度。此外，采用前K个相关伪标签计算目标域标签值提高了条件分布计算准确率和模型迁移泛化能力。JGSWD模型的有效性通过CWRU轴承数据集、XJTU-SY轴承数据集和往复压缩机轴承数据集得到了验证。在CWRU轴承数据集和XJTU-SY轴承数据集上的试验结果表明，JGSWD方法的平均分类准确率约为99%。从DLE到DRS的迁移试验结果表明，JGSWD方法的平均分类准确率约为97.56%，JMMD约为93.13%，DANN、MK-MMD和CORAL约为91%，S-only仅约为83%。JGSWD方法比其他方法具有更高的分类精度和更好的迁移性能，可为滚动轴承故障诊断提供一种新的有效方法。