巧用例子，让概念教学彰显数学本质——以“倒数的认识”为例

江苏南京市栖霞区靖安小学（210057） 李子豪

数学概念是数学知识的重要组成部分，对数学概念的掌握程度直接影响着后续数学知识的学习。近些年概念教学越来越受到重视，越来越多的研究者开始研究影响概念学习的因素。例子在这些因素当中占有一个很重要的地位。从狭义的角度来说，概念教学中的例子主要是正例和反例；从广义的角度来说，在教学中所使用的每一道例题都属于例子。概念教学以明确概念的内涵和外延作为主要目标，这就意味着在概念教学中需要使用一定数量的例子。心理学的研究也表明，学习者倾向于把例子作为获得信息的主要来源。那么，如何在概念教学中合理地使用例子成为一个亟须解决的问题。本文以“倒数的认识”一课为例进行探索。

表1呈现了三个版本教材关于“倒数”的编排。

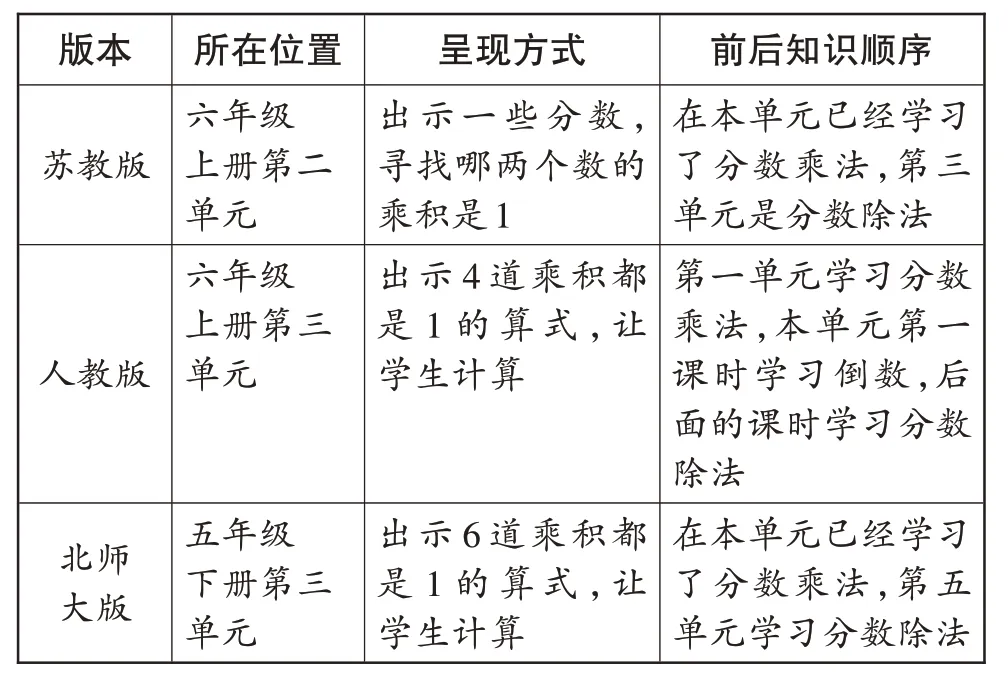
表1 三个版本教材中的“倒数”

从表1 可以看出，为了给分数除法做铺垫，“倒数”都被编排在分数乘法和分数除法之间，只有北师大版教材把“倒数”编排在五年级。从呈现方式的来看，人教版教材和北师大版教材均采用相同的呈现方式，即直接利用乘积是1 的例子来引入，而苏教版教材虽然没有这样做，但是指向性也非常明确。这些引入方式固然有开门见山的好处，但是否在概念引入的环节显得太过“着急”和“直接”了？怎样使用这些例子才能更好地让学生经历概念的发生和发展过程？

【教学片段一】巧用生成的例子引入概念

师（出示一些分数，略）：这里有一些分数，现在，请你们每次从这些分数中选2 个并算出它们的乘积，我说停的时候就停，看看谁写得多。开始！

（学生开始计算）

师（出示三位学生写的算式，略）：请观察这些算式，哪些比较特殊？为什么？

师：数学家也觉得这样的算式比较特殊，对乘积是1 的两个数给出了名称——乘积是1 的两个数互为倒数。怎样理解“互为”这两个字？能结合这个例子来说一说吗？

师：很好。如果甲、乙两个数满足“甲×乙=1”，那我们就说甲的倒数是乙，反过来也可以说乙的倒数是甲。现在，谁来照样子说一说和这两道算式中哪些数互为倒数？

教师对教材的引入方式做了一点改变，没有直接让学生去寻找乘积是1 的两个数，而是让学生在一定的时间里自由计算，这样做的目的有两个。

其一是让学生经历概念的发生和发展过程。直接点明乘积是1 固然有直入主题的好处，但是从数学史的角度来说，倒数概念的产生源于分数除法的需要，也就是说，倒数源于运算，是在运算过程中产生的。而在有限的时间里，学生为了能写出更多的算式自然会发现一些“好算”的算式，这样不仅能够复习前面所学的分数乘法，还能够让学生经历倒数概念产生的原始活动，从而对倒数概念有初步的认识，同时，学生自主生成的这些例子也成为概念教学的重要资源。

其二是让学生经历概念分类的过程。认知心理学认为，概念是分类的产物，是分类活动在学习者头脑中的表征，学习者学习概念就是希望通过一定的规则对具有明显特征的事物进行分类。在上述教学片段中，当教师询问学生“请观察这些算式，哪些比较特殊”的时候就是让学生经历分类的活动，通过这样的分类活动，学生容易从整体上把握概念，对概念的内涵有一个初步的认识，有利于提升学生的概括能力。

【教学片段二】选用合适的正反例明确概念

“倒数”概念具有两个本质属性——乘积是1和两个数，也存在一个无关属性——数的类别。而“互为”体现了两个数之间的一种关系，这种关系在说法上就需要注意。心理学研究表明，概念的正例所传递的信息最有利于概括，而概念的反例所传递的信息最有利于辨别。迄今为止，有大量的理论和实践研究表明概念的正反例在概念的建立和辨别阶段具有不可替代的作用，正反例在概念教学中的作用被一致认可。那么，如何在概念教学中选用合适的正反例呢？

笔者认为，在概念教学中所使用的正反例应该“互相匹配”，这里“互相匹配”的意思是所选用的正例和反例应该仅仅在概念的某一个本质属性上发生变化，而在其他的本质属性和无关属性上保持一致。变易理论认为，如果人们要识别出事物的某个属性，那么这个事物就必须在保持其他属性不变的前提下让那个属性在某个维度上发生变异，这样那个属性才能被识别出来。比如，第1 题的三个选项在数的类别、运算结果和参与运算的数的数量上保持一致，仅仅在运算的类别上发生了变化，通过这道选择题，学生马上就能识别出倒数概念的一个本质属性，即乘积是1。第2 题的三个选项在运算类别、运算结果和数的类别上均保持一致，仅仅是参与运算的数的数量不一样，这道选择题再一次让学生识别出倒数概念的另一个本质属性，即倒数是两个数之间的关系。这三道选择题起到了明确概念的内涵和及时评价的作用。

【教学片段三】利用有梯度的例子深化概念

师：你是怎么找到它们的倒数的？

生1：交换它们分子和分母的位置。

师：大家同意生1的说法吗？

生（齐）：同意。

生2：我是把它作为一种检验的手段，看看它们俩的乘积是不是1。

师：一个真分数或者假分数，交换它的分子和分母的位置，再跟原来的数相乘，结果怎样？

生（齐）：肯定是1。

师：真分数和假分数的倒数可以怎么找？

生3：直接交换分子和分母的位置。

师：有没有疑问或补充的？

生5：带分数的分数部分不能是假分数，得是真分数。

师：还有吗？

师：那正确的答案是什么？

这个阶段不仅是让学生掌握找倒数的技能，也是在帮助学生厘清概念的外延、深化对概念的理解。教师首先让学生尝试找真分数或假分数的倒数，在解决这个问题之后才让学生尝试找整数、带分数和小数的倒数。从知识的难度上，体现了由易到难的顺序；从例子的呈现方式上，先呈现概念最中心的正例，即原型，再逐渐由里往外，出示一些变式后的例子。真分数和假分数是倒数概念的原型，概念的原型具有该概念最多、最典型的特征，能让学生在短时间内最大限度地表征概念，所以先呈现真分数和假分数能让学生对于“找倒数”迅速地形成一定的认识。但是原型携带的概念特征会误导学生，这在找带分数的倒数中就体现了出来，有学生受负迁移影响，直接把带分数的分子和分母交换了位置，这就需要及时纠正。

在概念教学中用例子帮助学生形成观念时，要紧紧围绕概念的定义。上述教学片段中，无论是真分数、假分数，还是带分数，学生检验自己找的倒数对不对都是用概念的定义去验证，这与教学目标是相符的：我们希望学生在判断一个刺激物是否属于该概念时使用的是概念的定义，而不是拿它与概念的原型做对比后观察相似程度，因为后者往往会得到错误的答案。

在概念教学中还要明确所使用的每一个例子的目的，如上述的真分数和假分数，使用它们的目的不仅是让学生学会找倒数的方法，还需要通过对比让学生掌握相应的写法。

【教学片段四】搭配综合性的例子应用概念

师：请同学们在做这四组题的时候一边找倒数一边思考有没有什么规律。

生1：第（1）组，真分数的倒数是假分数；第（2）组，假分数的倒数是真分数；第（3）组，几分之一的倒数是几；第（4）组，几的倒数是几分之一。

师：你们同意吗？

生（齐）：同意！

师：他说“假分数的倒数是真分数”，大家同意吗？

生2：我不同意。

师：为什么？

师：其实，关于倒数的规律不止于此，比如在同号情况下，一个数越大，它的倒数越小；一个数越小，它的倒数越大。

莱什和兰多认为：评价学生对于概念的理解，要从四个方面着手，即感知、表征、联结和应用。也就是说，教师选用的例子不仅要包含多个有联系的知识点，还要有一定的推理层次，能综合考查学生对于相应概念的理解。

总之，教师在概念教学的过程中不能滥用例子，在概念引入、概念明确、概念深化和概念运用的环节都要积极地使用例子，但要遵循一定的原则和逻辑，只有会用例子、善用例子，数学课堂才会因“例”而精彩！