理性精神培养:审辩式学习的行动与省思
江苏苏州高新区实验小学校(215010) 黄海滢
“数学教育的核心任务是发展理性思维、培育理性精神”。《义务教育数学课程标准(2022 年版)》在“核心素养”之“会用数学的思维思考现实世界”中明确指出:发展质疑问难的批判性思维,形成实事求是的科学态度,初步养成讲道理、有条理的思维品质,逐步形成理性精神。张乃达先生在《数学证明和理性精神》中也谈到:“理性精神的缺失是我国文化的痛疾,这对社会的发展已经造成了巨大的伤害。”基于此,在数学教学中,坚持对学生进行审辩式思维培养,引导学生开启审辩式学习模式,开展理性精神教育非常必要。
一、内涵厘定:审辩式学习与理性精神的概念阐释
审辩式学习是对《中庸》中“博学之,审问之,慎思之,明辨之,笃行之”的创造性转化与创新性发展。“学、问、思、辨、行”是审辩式学习的特征,其核心在于审辩式思维的培养。
理性精神是一种信念,是指依靠思维能力对感性材料进行抽象和概括、分析和综合,以形成概念、判断或推理的理性认识活动并用于寻找事物的本质、规律及内部联系的精神。
审辩式学习与理性精神之间有着密不可分的关系,都指向严谨思考、慎思明辨、追求真理、实事求是、积极反思、勇于怀疑和批判、不断创新。审辩式学习的教育目的就是指向理性精神的培养。
二、问题扫描:审辩式学习教育及理性精神培养的现状审视
1.教师的教学理念亟待更新
(1)追求教学过程的精致,忽略思维过程的表达
日常教学中,特别是在公开课教学中,为了追求教学过程的精致化和标准化,教师往往会按照预先设计好的教学过程进行教学。但过程设计过细、预设过多,学生只能按照教师设定的教学流程进行学习,而教师留给学生思考的时间和空间不足,学生缺少表达自己独特见解的时间,思维表达受限。
(2)偏向知识技能的训练,轻视思维能力的培养
受课堂教学时间的限制,要在有限的时间内完成教学任务,教师往往会直奔教学主题,教学过程偏向知识技能的训练,学生的学习以模仿和记忆为主,过度追求“怎么做”,而对“为什么”鲜少思考。这样,数学课堂成了训练“答题机器”的操作间,而不是开启心智的智慧场。
2.学生学习品质有待提高
(1)止步于思维长度和梯度的提升层面,难以实现感性到理性的飞跃
一些学生缺乏吃苦耐劳的精神,数学的枯燥也让他们认为数学很难,他们在遇到复杂问题时难免存在畏难情绪,解决问题时也是浅尝辄止,不做深入思考,这样是难以实现感性到理性的飞跃的。
(2)停留在解题技巧和能力的培养,无法进行思维和创新的联结
如果教学过度追求解题能力的培养,忽略思维能力的提升,就会导致学生急功近利,学习只停留在寻求“怎么做”的层面上。学生多数时候只是在“照葫芦画瓢”,对知识的深层思考不够,更不愿反思解题思路和尝试用多种思路解决问题,无法进行思维和创新的联结。
三、价值探析:审辩式学习及理性精神培养的价值意蕴
1.审辩式学习指向求是精神的培养
审辩式学习表现为一种求是精神,它要求教师和学生对待科学应持求真求是的态度。教师应从学生的差异性出发进行教学设计,要求学生对科学知识始终抱有好奇心,不断追求真理,并勇于表达自己的观点,在学习中不断地创新、求异,进而达到培养理性精神的目的。
2.审辩式学习指向批判性精神的培养
审辩式学习表现为一种批判性精神,它指向不盲从权威,具有反思意识的学习态度。教师要引导学生对知识、结论、观点、问题等进行积极思考,在判断、推理等过程中形成独特的见解,并勇于将自己的独立见解表达出来,在深度理解知识的基础上培养学生的理性精神。
3.审辩式学习指向探究精神的培养
审辩式学习表现为一种探究精神。数学探究是一种教和学的方式,更是一种教学价值取向。教师要引导学生在独立思考、动手实践、自主探索、合作交流中完成对学科知识的内化,并能运用理性思维进行判断和推理,在分析的基础上进行整合和重构,使学生的理性思维、探索能力和理性精神得以培养。
四、路径求解:指向理性精神培养的审辩式学习教学实践
1.紧扣教学内容特点,搭建审辩支架,指向理性精神培养
(1)在概念获得中思辨,感悟理性精神
数学概念是人类认识事物的关键凭据,教师应引导学生主动经历概念产生的全过程,体会概念产生的必要性和可能性,抓住概念中蕴含的重要信息,挖掘数学概念的内涵,在质疑、探究中发现概念的本质属性,体验探索、创新的乐趣,提升思维品质,感悟理性精神。
[案例]苏教版教材三年级上册“长方形的周长和面积”
师:刚才咱们一起认识了周长和面积,并且通过方格图进行了周长和面积的比较。想一想,周长和面积到底有哪些不同的地方?
生1:面积指的是面的大小,周长指的是边线一周的长度,面积和周长的意义是不同的。
生2:面的大小是数方格,边线一周的长是数边。
师:因为意义不同,所以测量的方法也是不一样的。
师:用同样大的正方形,拼成如图1 所示的图形。想象一下,如果拿掉其中一个正方形,图形的面积会怎样?周长呢?
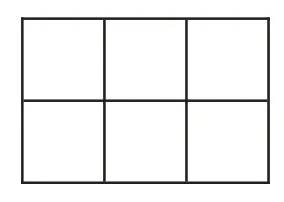
图1
生3:它的面积变小,周长不变。
师:具体说一说面积怎么变小了,周长怎么没有变。(学生回答略)
师(课件演示):看,面积确实会变小,周长则不变。
师(出示图2):去掉任意一个正方形,面积和周长还和原来一样吗?

图2
生4:去掉中间的一个正方形后就不一样。面积变小了,周长比原来的长了。
数学概念的教学一般都要经历概念的形成、概念的表述、概念的辨析、概念的应用等阶段。教师应引导学生通过观察、分析、比较、综合、抽象、概括等一系列思维活动,在不同形式的比较中全面把握概念的本质属性,进而培养学生的理性精神。
(2)在规律探究中思辨,聚焦理性精神
数学是一门严谨的学科,具有严谨的逻辑结构。数学教学的任务不应仅是让学生掌握结论性知识,还应让学生在自主探究的过程中,带着理性思维主动理解知识的本质,在辩证、辨析的过程中学会思考。这也是数学教学对学生理性精神培养的价值所在。
[案例]苏教版教材五年级下册“和的奇偶性”
师:任选两个自然数,算出它们的和,和是奇数还是偶数?(学生独立计算后在小组内交流)
师:这些算式能分类吗?它们有什么规律?
生1:奇数+奇数=偶数,偶数+偶数=偶数,奇数+偶数=奇数。
师:这些都是猜想,怎样验证你的猜想?
生1:再举一些例子。
师:举例是一个好方法,但能举出所有的例子吗?还有其他的方法吗?
生2:我用含字母的式子来证明。因为2x、2y是偶数,所以2x+1 是奇数。2x+1+2y=2(x+y)+1,所以“奇数+偶数=奇数”。
生3(出示图3):可以列表格,通过计算发现“奇数+偶数=奇数”。
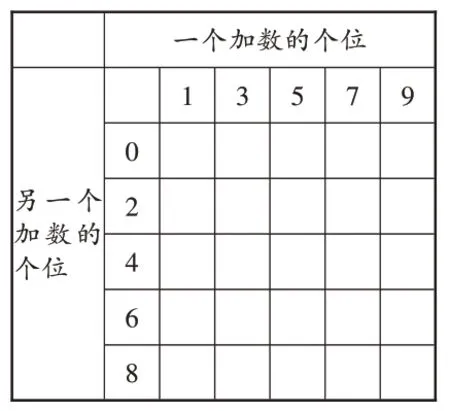
图3
生4(出示图4):这样看更方便。
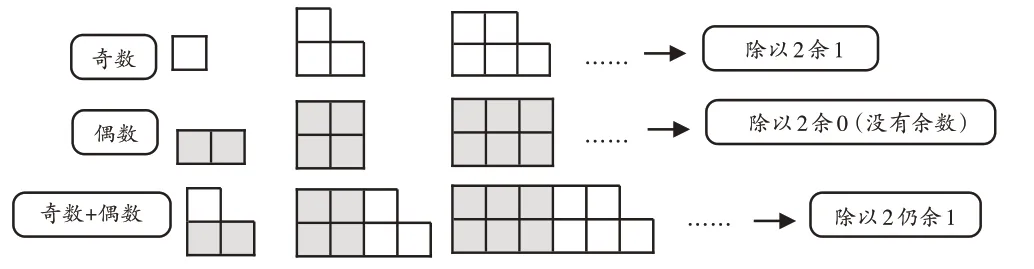
图4
推理是重要的数学思想方法,学生只有借助已有的知识经验对新知进行审辩,才能触摸到知识的本质,才能体会到数学思想的精髓。教学中,教师引导学生明确验证和推理的方法不只有举例,还有用字母表示数、列表格,以及数形结合的方法。将证明作为探索活动的自然延续和必要发展,理性精神自然能扎根于学生的心中。
(3)在问题解决中思辨,强化理性精神
《义务教育数学课程标准(2022 年版)》在总目标中指出,通过义务教育阶段的数学学习,学生能在探索真实情境所蕴含的关系中,发现问题和提出问题,运用数学和其他学科的知识与方法分析问题和解决问题。
[案例]苏教版教材六年级上册“解决问题的策略”
出示例1:小明把720 毫升果汁倒入6 个小杯和1 个大杯,正好都倒满。已知小杯的容量是大杯的,小杯和大杯的容量各是多少毫升?
师:你是怎样假设的?为什么要这样假设?假设后果汁的总量变没变?杯子的个数变没变?
生1:我把大杯换成小杯,这样就有9个小杯。假设把720 毫升果汁全部倒入小杯,那小杯的容量是720÷9=80(毫升),大杯的容量是80×3=240(毫升)。
生2:我把小杯换成大杯,这样就有3个大杯。假设把720 毫升果汁全部倒入大杯,那大杯的容量是720÷3=240(毫升),小杯的容量是240÷3=80(毫升)。
生3(出示图5):我用线段图帮助理解。
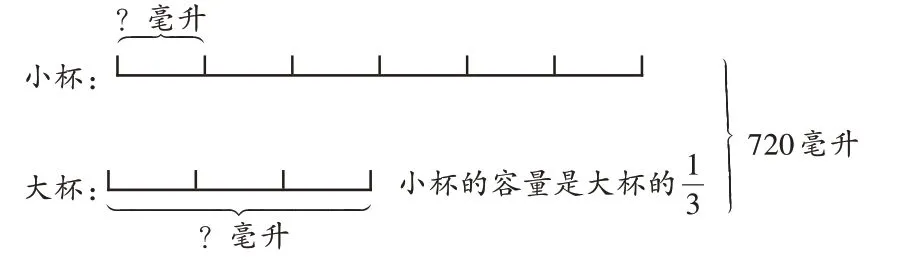
图5
生4:不管是把大杯换成小杯,还是把小杯换成大杯,都是把两种量假设成一种量。
审辩的过程是对问题的解决有自己的独特看法,而不是盲从。问题的解决往往不只有一种思路,教师要激发学生的探究意识,使学生在解决问题的过程中获得一些分析问题的经验,感受解决问题的一般过程,在用多种思路分析问题的审辩过程中发展实践能力和创新精神,培育理性精神。
2.设计多元教学方式,提供审辩媒介,实现理性精神培养
(1)创设问题情境,涵养质疑问难的理性气质
质疑是理性思维的核心,有疑问才能引发更多的思考,带着问题学习才会有更多的收获。“提出问题等于解决问题的一半。”教师在教学中应积极创设蕴含丰富数学背景的问题情境,以引发学生对所学知识的思辨,涵养学生质疑问难的理性气质。
[案例]苏教版教材六年级上册“求比值”
师:我们已经学习了求比值的方法,请大家一起来挑战吧。
出示:小明和小红买了同样价格的练习本,小明买4 本花了12 元,小红买6 本用了24 元。写出小明和小红买练习本所用钱数与本数的比,并求出比值。
生1:小明的是12∶4=3,小红的是24∶6=4。
师:3表示什么?4呢?
生1:3 表示小明购买的练习本的单价,4 表示小红购买的练习本的单价。
师:大家同意吗?
生2:题目中说他们买的练习本的价格是一样的,但是表示价格的比值又不同,题目有问题。
师:生2 具有敏锐的眼光,不只看结果的正确性,还看到了结果与题意矛盾。
面对同学的答案,生2 大胆地表达了自己的看法。教学中,教师就是要给学生质疑的时间,引发学生思辨,激发学生的探究热情,这是培养理性精神的起点。
(2)提供探究的时空,培育勇于自省的理性品质
《义务教育数学课程标准(2022 年版)》指出:发展质疑问难的批判性思维,形成实事求是的科学态度,初步养成讲道理、有条理的思维品质,逐步形成理性精神。教师要提供探究的时空,以唤醒学生的主体意识,使学生在自主、自觉的探究活动中获得对数学知识的感性认识后,向抽象的、理性的数学迈进。
[案例]苏教版教材四年级下册“三角形的三边关系”
师(出示图片,略):小明从家里到学校共有几条路线?如果是你,你会选择哪一条?为什么?
生1:我选择第三条。
师:让我们一起通过摆小棒来验证你的猜想。
师:老师为每个小组准备了一些小棒,请任意拿出三根,摆一摆,看看发现了什么。
生2:我们的是2、3、6,围不成三角形。
生3:我们的是3、4、5,围成了三角形。
生4:我们的是2、3、5,围不成三角形。
师:看来,不是任意三根小棒都能围成三角形的。这是为什么呢?我们一起把其中任意两条边的长度加起来,和第三边做比较。
生5:2+3<6,2+3=5,这两种都不能围成三角形。
生6:两边的和小于或等于第三边就不能围成三角形。
生7:任意两条边的和大于第三边才能围成三角形。
师:“任意”是什么意思?
生8:不管是其中的哪两条边。
师:是的,三角形的两边之和大于第三边。现在你能用三角形的三边关系解释为什么选第三条路线吗?
“理性思维是一种辨证思维”,这是认识的高级阶段。教师要重视提出问题、提出猜想、验证猜想,让学生在观察、联想、类比、推理、归纳、实验、反思的过程中进行理性探索,进而获得对知识的真理解,并在积极自省中实现知识的建构。
(3)引“说数学”的习惯,指向追根究底的精神内核
数学是思维的体操,语言是思维的外壳。数学教学的目的不应只是追求结论,还应重视质疑和说理的环节。因此,教师应引导学生“说数学”,经历“说”的过程,让学生的探究、归纳和逻辑推理能力得到充分训练,在“说数学”的过程中,指向追根究底的精神内核。
[案例]苏教版教材四年级下册“多边形的内角和”
师:我们已经知道了三角形的内角和是180度,那四边形、五边形、六边形的内角和分别是多少度呢?你想从哪一种图形开始研究?为什么?
生1:四边形,因为四边形是边数较少的图形。
师:好,那就从四边形开始研究。怎样求这个四边形的内角和?(出示四边形,图略)
生2:量出四边形4个角的度数后全部加起来。
生3:像研究三角形的内角和一样,把四边形的4个角撕下来拼在一起,正好是360度。
生4:我把四边形分成2个三角形,四边形的内角和就是360度。
师:这几个同学的方法中,谁的最简便?
生5:生4的。
师:把四边形分成2 个三角形,这样就把求四边形的内角和转化成了求2 个三角形的内角和之和,这种方法很巧妙。继续探究五边形、六边形的内角和。如果是有很多边的多边形呢?
语言与思维是紧密联系的,语言是思维的外显形式。关注思维品质的提升不仅要让学生知其然,更要让学生知其所以然。教学中,学生从“听数学”到“做数学”再到“说数学”,清清楚楚地表达自己的思想,厘清自己的想法,在“说数学”的过程中,学生的逻辑思维能力和理性精神自然生发。
审辩式学习的重要指向是理性精神的培养。数学理性精神是数学学科的精髓,理性精神的培养是数学教育的核心任务。作为数学教师,要积极为学生创设可思能辩的教学情境,鼓励学生质疑问难、主动探究,养成大胆表达、敢于审辩的思维品质,在“说数学”的过程中发展理性精神,用数学的理性光芒来提升数学核心素养。

