根据“货郎担”理论优化果蔬产品冷链配送路径

胡光萼

摘 要：为提高果蔬冷链运输的配送效率，降低成本，根据“旅行商”理论，应以最短路径、最小费用为目标，建立配送網络优化模型，并结合果蔬运输的案例运用线性规划求解。分析结果表明：经过优化后，配送距离和运输费用都有了明显的改善，更能满足市场果蔬运输的需求。

关键词：果蔬运输；旅行商理论；规划求解

中图分类号：F50文献标志码：ADOI：10.13714/j.cnki.1002-3100.2023.12.034

Abstract： In order to enhance the efficiency of cold chain distribution for vegetables and fruits and lower the cost， according to TSP theory， the distribution network optimization model should be established with the shortest path and minimum cost as the goal， and the liner programming should be used to solve it combined with the case of fruit and vegetable transportation.  The consequence shows that after optimization， both the distance and transport cost decreased obviously， which could better meet the requirements of distribution service in the market.

Key words： transport of vegetables and fruits; TSP theory; programming solver

运输新鲜果蔬和常温产品的区别在于新鲜果蔬采摘后仍然是具有生命的活体，并且还在不断地进行呼吸作用，消耗着养分和水分。果蔬产品的品质会在运输过程中不断下降，而且由于新鲜果蔬富含水分并且容易在采摘和运输过程中遭受机械伤，所以极易受到外界微生物的侵染，从而导致其腐败变质，失去商品价值[1]。新鲜果蔬的这些特点决定了找到从果蔬生产基地到各个配送点的最优配送路径是企业生存获利的关键。在日常的配送活动中，由于路径选择不合理而导致的运费成本居高不下等问题比较突出。如何通过建立一个合理的配送模型来优化配送路径，进而得到一个配送路线最短或者配送成本最低的方案是本文要讨论的重点。

果蔬冷链运输多数采用的是公路运输方式，可以依靠自己的车队或者外包给第三方物流公司完成。一般来说，同一个果蔬生产基地负责配送的区域相对稳定，配送对象的果蔬订购数量也相对稳定，而本文主要考虑一个生产基地、同一批货物、几个需求地点的果蔬配送问题。

1   “货郎担”理论介绍

“货郎担”理论是说一个销售人员要去N个城市推销商品，他从一个城市出发，需要经过所有城市后回到出发地，并且每个城市只能去一次，应该怎样选择路线才能使总行程最短或者总运费最少呢？根据“货郎担”理论，本文要通过规划求解的方法，找到从生产基地到各个配送点配送果蔬的最短路径和运输成本最小的路径[2]。

2    以路径最短为目标建立配送模型

2.1    果蔬冷链案例描述

位于上海的果蔬生产基地S0向位于周边地区的六个配送点配送果蔬28.5t，采用公路运输方式，每个配送点只能进出一次，车辆从果蔬生产基地向各个配送点运输果蔬产品，在配送过程中到达并且只能到达每个配送点一次，最后空车返回生产基地。各个配送点的需求量见表1。

2.2    建立模型

果蔬冷链运输情况复杂，需要准确把握配送的时间和数量。我国公路运输冷链车辆一般为隔热车辆，没有配备专门的制冷装置。所以，研究从生产基地到各个配送点的最短距离成为优先考虑的问题。尤其是夏季，果蔬更容易腐败变质，因此更需要及时配送到配送点。见表2。

该生产基地原来的运输路线是S0→S1→S2→S3→S4→S5→S6→S0。总路程为624公里，采用3辆10t车运输，生产基地3辆车单位配送运输费用为16.72元/（辆·km），空返费用为6.95元/（辆·km），总费用为24 391.14元。

原来的生产基地计算运输费用采用的计量单位是元/（辆·km）。但在实际运输过程中，车辆到达各个配送点后会卸载一部分货物，这时实际载重就会发生变化。因此，对于重车采用元/（t·km）计算运费更合理；对于空返车辆，因为没有载重，则可以使用原来的计费方式元/（辆·km）。根据市场调查的情况，本文采用的计费标准为：重车1.8元/（t·km），空车返程取4元/（辆·km）[3]。

2.2.1    决策变量

首先设一个决策变量Xij，含义是：

1 选择走节点i到节点j的路径，

Xij={

0 不选择走节点i到节点j的路径。

2.2.2    约束条件

对于网络中的节点S1，车辆都要经过并且只经过一次，也就是说对于节点S1来说都要走入一次。剩下的S2—S6同样如此。

同样，对于所有的节点，都需要走出一次。

从S0出发，经过所有配送中心后，最后回到S0，整个配送路线必须是一个完整的回路，对于其中连续的n个节点要满足以下条件。

2.2.3    目标函数

以配送距離最短为规划目标，节点i到节点j的距离为Lij，则目标函数为：

综上，果蔬冷链完整的配送路径数学模型如下。

目标函数：Zmin=Σ6i=0Σ6j=0Lij×Xij（i≠j），

Σ6j=1Xij=1（i=0，1，2…6；j≠i），

{Σ6j=1Xji=1（i=0，1，2…6；j≠i），

Xij=0或1。

2.3    模型求解

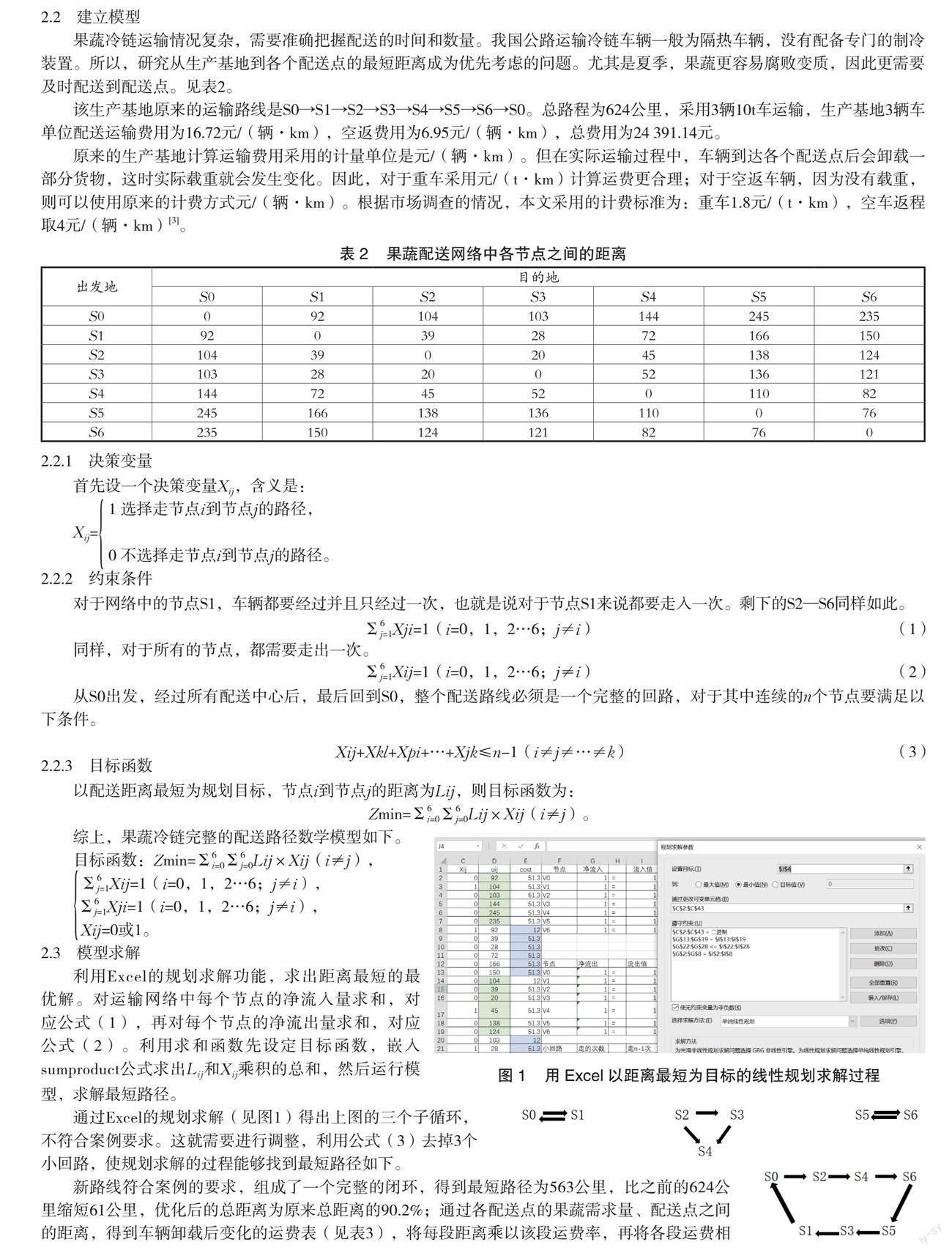
利用Excel的规划求解功能，求出距离最短的最优解。对运输网络中每个节点的净流入量求和，对应公式（1），再对每个节点的净流出量求和，对应公式（2）。利用求和函数先设定目标函数，嵌入sumproduct公式求出Lij和Xij乘积的总和，然后运行模型，求解最短路径。

通过Excel的规划求解（见图1）得出上图的三个子循环，不符合案例要求。这就需要进行调整，利用公式（3）去掉3个小回路，使规划求解的过程能够找到最短路径如下。

新路线符合案例的要求，组成了一个完整的闭环，得到最短路径为563公里，比之前的624公里缩短61公里，优化后的总距离为原来总距离的90.2%；通过各配送点的果蔬需求量、配送点之间的距离，得到车辆卸载后变化的运费表（见表3），将每段距离乘以该段运费率，再将各段运费相加，得到总运输费用为15 517.5元，为原来费用的63.62%。

3    以配送费用最小建立模型

和之前的模型一样操作，利用excel的规划求解功能（见图2），求出运输费用最小的最优解。因为每个节点都需要进和出各一次，所以对每个节点的净流入量求和，对应公式（1），再对每个节点的净流出量求和，对应公式（2）。利用求和函数先设定目标函数，目标函数为：Zmin=Σ6i=0Σ6j=0Lij×Xij×Cij（i≠j），Cij代表每段路径的运费。嵌入sumproduct公式求出Lij、Xij和Cij乘积的总和，然后运行模型，求解最小费用。输入约束条件后，得到两个子循环如下。

经过调整，利用公式3消除子循环，等到新的循环如下。

根据线性规划的结果，以费用最小为目标优化后的果蔬配送路径的总距离为588公里，比原来缩短36公里；通过各节点果蔬的需求量和节点之间的距离，得到车辆卸载后变化的运费表（见表4），将各段运费相加求得总运费为12 880.5元，比原来的费用减少11 510.64元。

4    结    语

本文针对果蔬的配送路径问题，基于“货郎担”理论建立了果蔬配送路径的优化模型，并将该模型应用于某地的果蔬配送中，同时对配送方案进行了以最短距离、最小费用为目标的优化。以配送最短距离为目标的优化结果是：总距离为原来总距离的90.2%，总运输费用为15 517.5元，为原来费用的63.62%；以配送最小费用为目标的优化结果是：总距离为原来的94.2%，总费用为原来的52.8%。该模型为果蔬的冷链配送提供了理论依据，管理者可以根据实际情况来决定采用哪种配送路径，如果是寒冷的冬季，室外温度满足大部分果蔬运输的要求，那么短途运输考虑总成本最低路线即可；如果是炎热的夏季，短途运输采用的是没有制冷设备的隔热车厢，那么还是应以最短距离作为最优配送路线为好。

参考文献：

[1] 李建春．农产品冷链物流[M]．北京：北京交通大学出版社，2014.

[2] 叶向．实用运筹学[M]．北京：中国人民大学出版社，2013.

[3] 孙敬博，冯鹏程．基于TSP理论的弹药配送路径优化[J]．军事交通学院学报，2019，21（8）：91-95.