机床主轴精度特性的弹性冗余空间机构参数研究

摘要：阐述零件表面几何特征随静、动联接面的弹性映射与运动映射规律，将多零件几何误差转换为旋转轴芯的误差运动，并以悬浮凸轮复演轴芯误差运动为准则构造等效凸轮轮廓；建立机构结构、凸轮轮廓、构件弹性等与机床主轴结构、零件表面几何特征以及零件弹性之间的等效关系，将机床主轴精度随各影响因素的变化关系分析问题转换为机构输出运动随机构几何与弹性参数的变化关系分析问题，并以典型机床主轴为例进行计算等效和试验验证。

关键词：机构；精度特性；机床主轴；误差传递

车床主轴精度是衡量主轴性能的重要指标，通常以主轴的位置误差和轴芯运动轨迹误差描述，即实际旋转轴与理想旋转轴之间的位置、形状与运动的差异，这种差异随零件几何特征与物理性能、载荷、运动等因素的变化规律形成了车床主轴的精度特性。目前关于车床主轴精度及其关键部件精度（轴承）的研究较多，包含了零件几何误差、装配误差、静态特性、动态特性、热特性等方面[1-6]。为此，在文献[7]中提出回转副精度特性的弹性冗余空间机构模型与分析方法，将机床主轴精度特性分析转化为等效机构的位移、运动与力分析，为实际工况下的机床主轴精度特性分析提供模型与方法。

本文以简化的典型机床主轴为例，阐述弹性冗余空间机构模型中几何与物理参数的意义、等效过程以及计算方法，为各种车床主轴结构提供参考。

一、弹性冗余空间机构基本方程与参数

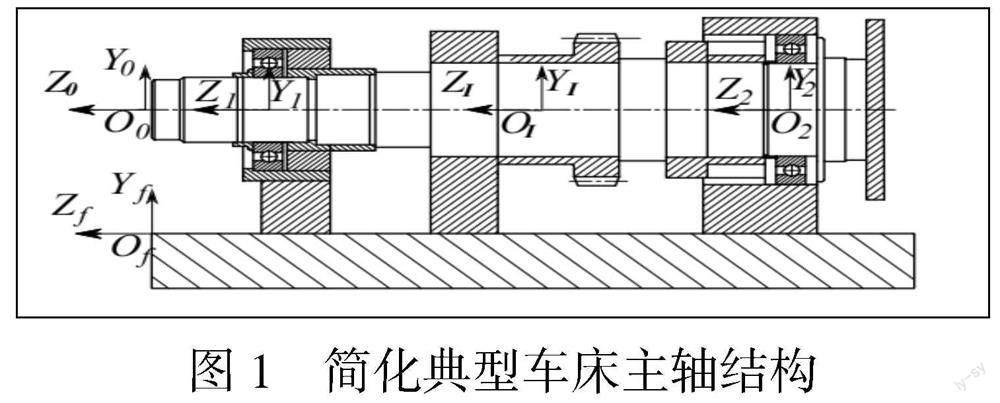
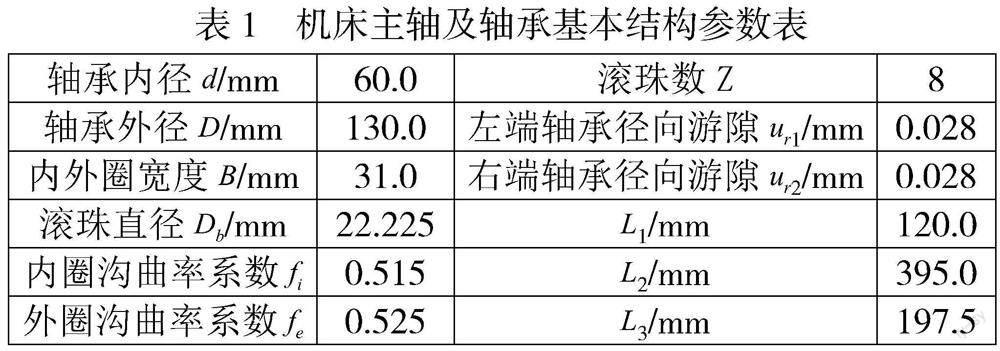
以图1所示的简化典型机床主轴为对象，其旋转轴两端各由一个深沟球轴承（型号6312）支承，右端端盖与力传感器相连，以便在试验中调节并测试轴承预紧力。以OP1截面作为机床主轴旋转精度的测量面（输出截面），OP2截面作为加载截面（输入截面），与机构等效相关的机床主轴及轴承基本结构参数见表1。

图1中机床主轴属于对称双支点单向固定滚动轴承结构，其等效弹性冗余空间机构模型为两端共10个凸轮从动件对应10个凸轮轮廓。

（一）凸轮轮廓方程

（1）

当V=Z时，i=1、j=2或i=2、j=1。上式展开共10个方程，包含如下2组参数：①表示凸轮i在坐标系（OXYZ）f中的位置和姿态参数，是机构基本方程的待求变量。②为凸轮坐标系（OXYZ）i下的凸轮轮廓方程，是机构的几何参数，由机床主轴零件的表面几何特征等效计算。

（二）机构位移方程

（2）

（3）

（4）

上述展开共10个位移方程，包含如下5组参数：①ri（V=X，Y，Z）为凸轮i在坐标系（OXYZ）f中的位置矢量，是机构基本方程的待求变量。②riVj （V=X，Y，Z）为凸轮矢径，即凸轮中心到凸轮从动件接触点的矢量，是计算中间变量，由凸轮轮廓方程与从动件轴线方程联立求解。③ LiVj （V=X，Y，Z）为凸轮从动件长度矢量，是机构的几何参数，由机床主轴零件的结构参数等效得到。④ δiVj   （V=X，Y，Z）为从动件位移矢量，是机构基本方程的待求变量。⑤LDi、LBi、LS为等效机构的几何结构参数，由机床主轴的结构参数等效确定。

（三）静力平衡方程

（5）

（6）

上述展开共10个静力平衡方程，包含如下3类参数：①FPk、MPk、rPk分别为旋转轴的外载荷、外力矩及其位置，是机构的已知输入参数。②FiVj （V=X，Y，Z）中为凸轮从动件对凸轮的作用力，是机构基本方程的待求变量。③riVj f  （V=X，Y，Z）为凸轮上载荷作用点的位置矢量，即机架坐标原点到凸轮从动件接触点的矢量，是计算中间变量，由凸轮轮廓方程与从动件轴线方程联立求解。

（四）机构物性方程

（7）

（8）

上述展开共16个位移方程，含如下5组参数：

①FiVj K为从动件支承弹簧的载荷，为计算中间变量，与公式（5）、（6）中的载荷FiVj 存在如下关系：

（9）

②kiVj 为从动件支承弹簧刚度，是机构的弹性参数。

③ε12为两端凸轮之间的相对位移与转角，是机构基本方程的待求变量。

④CSn为凸轮连接轴柔度，是机构的弹性参数。

⑤Pn=[FPn，MPn]T为凸轮轴上的等效载荷，是机构的已知输入参数。

综上所述，机构基本方程中的参数分类见表2。

二、弹性冗余空间机构的几何参数等效

（一）机构结构参数等效

机构结构参数（LiVj 、LDi、LBi、LS）取決于机床主轴的结构与尺度。机构两端凸轮截面间距LS =395mm对应轴承两端轴承跨距，机构径向从动件机架所在圆的直径LDi= 117.233mm（i=1，2）对应轴承外圈滚道底径，机构轴向从动件机架到端面凸轮距离LBi=15.5mm（i=1，2）及轴向从动件的初始长度= 15.5mm（i=1， j=2或i=2， j=1）对应轴承中间截面到轴向定位面的距离，机构径向从动件初始长度=22.225mm、=22.225mm（i， j=1，2）对应轴承内圈沟道底径到外圈沟道底径的距离。

建立基准坐标系（OXYZ）f取左端轴承座与基座的配合面，按机床主轴装配关系建立误差链，可得坐标系（OXYZ）fi的位姿参数εfi。

（二）凸轮轮廓等效

凸轮轮廓方程取决于机床主轴各零件表面几何特征及其随静态与动态连接面的映射。

1.零件几何特征简化与表述

零件回转表面的几何特征可简化为若干截面测量，对轴承外圈外圆面与内圈内孔面与的测试轮廓分别进行测试，采用测试截面间隔1mm，每个截面测量3600个等分点的轮廓数据。

采用傅立叶级数对各截面的实测轮廓进行拟合并简化，以各截面的拟合轮廓数据为基础，为将表达式简化，在此以柱坐标系下曲面的一般方程表示：

S：r                    （10）

式中表示零件理想表面，表示零件表面几何误差。

2.零件几何特征的弹性映射

图1中轴承座-基座配合面距轴承座内孔面较远且轴承座刚度大，轴承座内孔面上几何误差的弹性映射量小，而轴承座-轴承外圈配合面为过渡配合，零件弹性变形小，故此处仅计算轴-内圈配合面的弹性映射。

根据轴承内圈与轴之间静联接的弹性映射关系，以偏移节点法[8]使各零件表面形状按拟合的几何误差分布。根据左右两端轴承内圈与轴联接的计算位移云图，如图2所示，a1为内圈内孔面形状误差、a2为轴表面形状误差（含过盈）、a3为内圈内孔面与轴表面形状误差之和，a4为内圈滚道上的节点位移，近似公式为：

（11）

三、弹性冗余空间机构的弹性参数等效

（一）凸轮从动件支承弹簧刚度计算

分别建立左右两端轴承支承结构的有限元模型，计算等效轴承约束的刚度。对于案例中的机床主轴结构，除轴承外其他零件弹性变形与载荷呈线性，该部分刚度记为kiSj V，计算结果如表3所示。其中，支承约束刚度可按弹簧串联的刚度公式计算。

四、弹性冗余空间机构模型求解

（一）机构基本方程求解与参数意义

由于等效凸轮轮廓方程较复杂，且从动件支承弹簧刚度为非线性，机构基本方程需采用数值方法迭代求解，过程如下。

（1）迭代变量与初始值：以机架坐标系（OXYZ）fi中的Ri为迭代变量，其值取为Ri0=（0，0，0，0，0，0）；凸轮矢量ri=（xi，yi，zi），由Ri确定。

（2）凸轮轮廓方程：RiVjf =（xiVjf yiVjf ，ziVjf ），并计算点RiVjf 处凸轮曲面法向量niVj f 、从动件轴线夹角αiVjf 、凸轮矢径riVj   =（xiVjf -xi，yiVjf -yi，ziVjf -zi）。

（3）机构位移方程：将ri、riVj代入机构位移方程，求得从动件位移δiVj  。

（4）物性方程：将δiVj      代入从动件物性方程，求得弹簧回复力FiVj  k，进而由公式（9）计算从动件对凸轮的支反力FiVj ；由选择轴物性方程求解两端凸轮相对位移ε。

（5）静力平衡方程：将FiVj代入静力平衡方程，由于Ri为假设值，方程左端不一定为零，进而得到凸轮的位置变化量εiF。

（6）迭代求解：命令R1=R1+ε1F、R2=R2 +ε2F +ε12返回第（1）步进行迭代求解。

按步骤（1）～（6），可求解轴在任意转角与载荷时机构基本方程变量。如轴转角、输入载荷FPY2 =3000N时，两端凸轮位姿参数Ri分别为R1 = [1.99， -10.92， 36.59， -1.30×10-4， 1.92×10-5， 0]，R2 = [-0.54， -10.85， -394963.41， 1.28×10-4， 1.92×10-5， 0），表示机床主轴两端轴承支承截面轴芯实际姿位与理想姿位的偏差；ε12=[0，5.09，0，2.58×10-4，0，0]，表示旋转轴的弹性变形；从动件位移δiVj  及载荷FiVj  k（或FiVj   ），表示机床主轴支承截面处的弹性位移与支承载荷（见表4）。

（二）机床主轴精度特性分析

以机床主轴在输出截面（OXYZ）P1处的旋转误差的Y向分量作为考察对象，轴低速旋转、输入载荷为FPY2 =3000N，进行计算，如图3所示。

仅考虑零件几何误差：以等效凸轮轮廓形状体现，令轴刚度和弹簧刚度为无穷大，如曲线a1。

仅考虑轴承约束刚度：以从动件弹簧刚度体现，令轴刚度无穷大且凸轮为理想圆r0和理想平面z0，如曲线a2。

仅考虑旋转轴刚度：以凸轮联接轴刚度体现，令从动件弹簧刚度无穷大且凸轮为理想圆r0和理想平面z0，计算结果为曲线a3。

几何误差、轴承刚度、轴刚度三种因素均取实际参数，综合结果为曲线a4。

在算例计算条件下，轴变形与轴承支承结构变形方向相反，零件几何误差在不同相位时对机床主轴精度影响不同，即零件几何误差、轴承约束刚度、旋转轴刚度对机床主轴精度的影响各异，且与机床主轴运动与载荷相关。

五、结束语

①弹性冗余空间机构的几何参数由机构结构参数与凸轮轮廓参数构成，其中机构结构参数与机床主轴结构参数对应，凸轮轮廓参数由零件表面几何特征及其随静、动联接面的弹性映射与运动映射等效。②弹性参数包括从动件支承弹簧刚度与凸轮联接轴柔度，支承弹簧刚度由机床主轴轴承支承结构的约束刚度等效，凸轮连接轴柔度由机床主轴旋转轴柔度等效。③通过分析机构输出位移与机构几何与弹性参数之间的关系，可求解机床主轴精度与各影响因素之间的联系。

作者单位：纪英男 洛阳电光設备研究所

参  考  文  献

[1]于洁，李松生，袁伟，等.考虑热变形影响的主轴轴承动态特性[J].航空动力学报，2018，33（02）：477-486.

[2]田久良，洪军，朱永生，等. 机床主轴-轴承系统热-力耦合模型机器动态性能研究[J]. 西安交通大学学报，2012，46（7）：1-7.

[3]栗世豪，张俊，唐宇阳，等.零件加工误差与机床几何误差映射关系建模[J].西安交通大学学报，2021，55（10）：50-59.

[4]余永健，陈国定，李济顺，等.轴承零件几何误差对圆柱滚子轴承回转误差的影响：第一部分 计算方法[J].机械工程学报，2019，55（01）：62-71.

[5]王涵，吴玉光.不同类型接触面机械零件装配误差的自动计算方法研究[J].机电工程，2021，38（06）：655-664.

[6]陈代鑫，刘适，陈龙波，等.数控机床某些特性对零件加工质量的影响分析[J].航空制造技术，2014（03）：63-66+70.

[7]王德伦，王智，董惠敏，等.回转副精度特性的弹性冗余空间机构模型[J].机械工程学报，2013，49（17）：110-122.

[8]李震，关先磊，钟锐，等.联合载荷下角接触球轴承的动态特性分析[J].机械工程学报，2020，56（17）：116-125.