基于IMU体对角线旋转的双轴旋转方案

查 峰, 位秋硕, 何泓洋, 李 豹

(海军工程大学电气工程学院, 湖北 武汉 430033)

0 引 言

惯导系统具备自主性强、可靠性高的特点,可以使载体航行更加隐蔽,因此常常被应用于潜艇、无人潜航器等军事装备[1-4]。由于缺少外部信息的校正,以及惯导系统自身器件误差以及工作环境的影响,导航误差随时间累积,经过长时间的航行,载体的导航误差将不可忽视[5-9]。目前主要采用提升惯性器件精度和旋转调制技术两种手段提高惯导系统精度[10-13]。其中,旋转调制技术是减小导航误差经济且有效的方式[14-18]。旋转惯导系统利用惯性测量单元(inertial measurement unit, IMU)规律性旋转以调制系统常值和慢变误差,因此旋转方案是决定系统精度提升的关键因素[19-25]。目前,常见的单轴、双轴旋转惯导系统均以IMU的某一个或两个方向惯性器件敏感轴作为旋转轴,通过改变旋转轴的旋转速度、方向、次序来设计不同的旋转方案。该方案简洁直观,空间关系简单,易于实现。Levinson[23]在20世纪80年代提出了旋转调制的概念。文献[25]在国内较早开展旋转方案研究,针对单轴旋转系统,研究了四位置旋转方案,并针对其主要误差特性进行了研究和分析。针对双轴旋转系统,提出了改进八位置和十六位置旋转方案。文献[6]在此基础上针对速度误差累积问题,提出一种改进的十六位置旋转方案。文献[26]针对十六位置旋转方案中转角过大问题,提出一种三十二位置的旋转方案。文献[27]针对刻度系数误差与IMU运动的耦合效应,提出一种综合误差抑制的旋转方案,减小了一个周期内的速度误差累积,取得理想效果。文献[28]针对双轴旋转方案进行了深入研究,为了解决光纤陀螺刻度系数稳定性较差且不宜采用传统旋转方案的问题,提出一种外环水平结构双轴光纤惯导系统的旋转方案。此外,文献[29]设计了一种四十八位置的双轴旋转方案,不仅可以用于误差调制,还可以用于惯导系统的自标定。上述旋转方案研究均是基于旋转轴与惯性器件敏感轴同向的前提。由于旋转轴与惯性器件敏感轴同向,因此在绕某一轴旋转时,该轴向上的惯性器件相关误差难以得到调制。文献[30]提出一种改进的单轴旋转方案,使旋转轴与IMU天向轴呈一定角度,以解决天向器件误差不能调制的缺陷,有效提高了单轴旋转系统的精度。在该方案中,由于器件误差未知,旋转轴夹角确定相对困难,在一定程度上限制了补偿效果。

本文提出一种基于IMU体对角线旋转的双轴旋转方案。方案不再以惯性器件敏感轴为旋转轴,而选取IMU 3个正交惯性器件的体对角线为水平旋转轴,选取与该轴正交的垂向轴为另一旋转轴。通过改变水平和垂向旋转轴的旋转速度、方向和次序实现双轴旋转。由于旋转轴与惯性器件均不同向,因此在旋转的任意时刻,3个方向的惯性器件误差均得到调制,最大程度地提高了系统精度。

1 旋转惯导误差模型

1.1 坐标系定义

惯性坐标系(设为i系):惯性坐标系的原点位于地球的中心,z轴沿地轴指向北极,x轴在赤道平面内指向春分点,y轴与z轴、x轴构成右手直角坐标系;

导航坐标系(设为n系):选取当地地理坐标系,导航坐标系的原点位于载体质心,x轴指向东向,y轴指向北向,z轴指向天向;

载体坐标系(设为b系):载体坐标系的原点位于载体质心,x轴通过质心指向载体右方,y轴通过质心指向载体前方,z轴通过质心指向载体上方;

安装坐标系(设为m系):3组陀螺仪、加速度计互相垂直,构成IMU,3组惯性元件分别为安装坐标系的x轴、y轴、z轴;

旋转坐标系(设为p系):在旋转调制初始时刻,旋转坐标系与载体坐标系重合。当IMU绕载体坐标系的x轴旋转时,旋转坐标系的x轴与载体坐标系的x轴重合,旋转坐标系的y轴和z轴绕旋转轴x轴以旋转角速度转动;当IMU绕载体坐标系的y轴旋转时,旋转坐标系的y轴与载体坐标系的y轴重合,旋转坐标系x轴和z轴绕旋转轴y轴以旋转角速度转动;当IMU绕载体坐标系的z轴旋转时,旋转坐标系的y轴与载体坐标系的y轴重合,旋转坐标系x轴和z轴绕旋转轴y轴以旋转角速度转动;双轴旋转调制一般选择绕x轴和z轴旋转。

1.2 系统误差源定义

常值误差(表示为ε)和随机误差(表示为σ):惯性器件在没有输入信号的情况下有输出信号。该输入信号以常值、随机规律变化。

刻度系数误差(表示为δK):将惯性器件的输出电压转换为角速度或加速度时产生的误差。刻度系数误差矩阵表示如下:

其中:k11、k22、k33为3个陀螺仪输出转换为角加速度时的转换系数。

安装误差(表示为δA):惯性器件的敏感轴与理想正交安装产生的夹角,设k12、k13、k21、k23、k31、k32为6个安装误差角。安装误差矩阵如下:

其中:k12、k13、k21、k23、k31、k32为3个陀螺仪安装时与理想安装产生的6个未对准夹角。

1.3 旋转惯导误差方程

在惯性导航系统中,基于角度误差定义的姿态误差和速度误差如下所示:

(1)

(2)

由惯性导航系统误差方程可以得到传统的旋转惯性导航系统误差传播方程,如下所示:

(3)

(4)

定义式(3)中第3项(设为En)为导航坐标系下的角速度误差,式(4)中第2项(设为Γn)为导航坐标系下的比力误差,展开式为

(5)

(6)

2 旋转方案的数学模型

2.1 传统旋转方案建模

文献[6]旋转方案基于旋转轴与惯性器件敏感轴同向的前提,其具体旋转方案可以表示为

(1) 绕Z轴正转180°,停留ts秒;

(2) 绕X轴正转180°,停留ts秒;

(3) 绕Z轴反转180°,停留ts秒;

(4) 绕X轴反转180°,停留ts秒;

(5) 绕X轴反转180°,停留ts秒;

(6) 绕Z轴反转180°,停留ts秒;

(7) 绕X轴正转180°,停留ts秒;

(8) 绕Z轴正转180°,停留ts秒;

(9) 绕X轴正转180°,停留ts秒;

(10) 绕Z轴正转180°,停留ts秒;

(11) 绕X轴反转180°,停留ts秒;

(12) 绕Z轴反转180°,停留ts秒;

(13) 绕Z轴反转180°,停留ts秒;

(14) 绕X轴反转180°,停留ts秒;

(15) 绕Z轴正转180°,停留ts秒;

(16) 绕X轴正转180°,停留ts秒。

表1 传统16位置旋转方案和ωp的表达式

2.2 本文旋转方案建模

本文方案在传统旋转方案的基础上,改变旋转轴的设定,选取IMU 3个正交惯性器件的体对角线为水平旋转轴,选取与该轴正交的为垂向旋转轴,如图1所示。

图1 倾斜旋转调制方案Fig.1 Tilt rotation modulation scheme

本文方案在文献[6]旋转方案的基础上,改变IMU在双轴转台上的放置方式,将IMU 3个正交惯性器件的体对角线为水平旋转轴,与转台内环轴平行,与该轴正交的为垂向旋转轴,与转台外环轴平行,且水平旋转轴与IMU的3个敏感轴夹角相等,如图2所示。旋转秩序与文献[6]中的旋转秩序一致。

图2 安装坐标系与旋转坐标系关系Fig.2 The relationship between installation coordinate system and rotation coordinate system

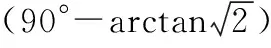
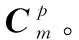
(7)

(8)

角速度误差和比力误差的展开式如下所示:

(9)

(10)

3 系统误差特性分析

3.1 姿态误差分析

首先讨论由常值误差、刻度系数误差和安装误差引起的姿态误差。

(1) 由常值误差引起的姿态误差:合理的双轴旋转调制方案都可以将常值误差调制为零,在此不再赘述。

(2) 由刻度系数误差引起的姿态误差:将式(9)中含有刻度系数误差的部分进行积分、累加,可获得每次旋转后由刻度系数误差产生的姿态误差变化幅度,如式(11)所示为一个旋转周期内(即经过十六次旋转后)由刻度系数误差引起的姿态误差。

(11)

(3) 由安装误差引起的姿态误差:将式(9)中含有安装误差的部分进行积分、累加,可获得每次旋转后由安装误差产生的姿态误差变化幅度,如式(12)所示为一个旋转周期内由安装误差引起的姿态误差。

(12)

将上述文献[6]和本文旋转方案相关数学表达式带入式(11)和式(12)中,可得到由刻度系数误差和安装误差引起的姿态误差。假设3组惯性器件的刻度系数误差相同,各轴向的安装误差相等,即设k11=k22=k33=k1,k12=k13=k21=k23=k31=k32=k2,如表2～表3所示。

表2 传统16位置旋转方案由刻度系数和安装误差引起的姿态误差

表3 改进方案由刻度系数和安装误差引起的姿态误差

将表2和表3中的刻度系数误差和安装误差引起的姿态误差幅度变化如图3～图4所示。

图3 由刻度系数误差引起的姿态误差Fig.3 Attitude error caused by scale factor error

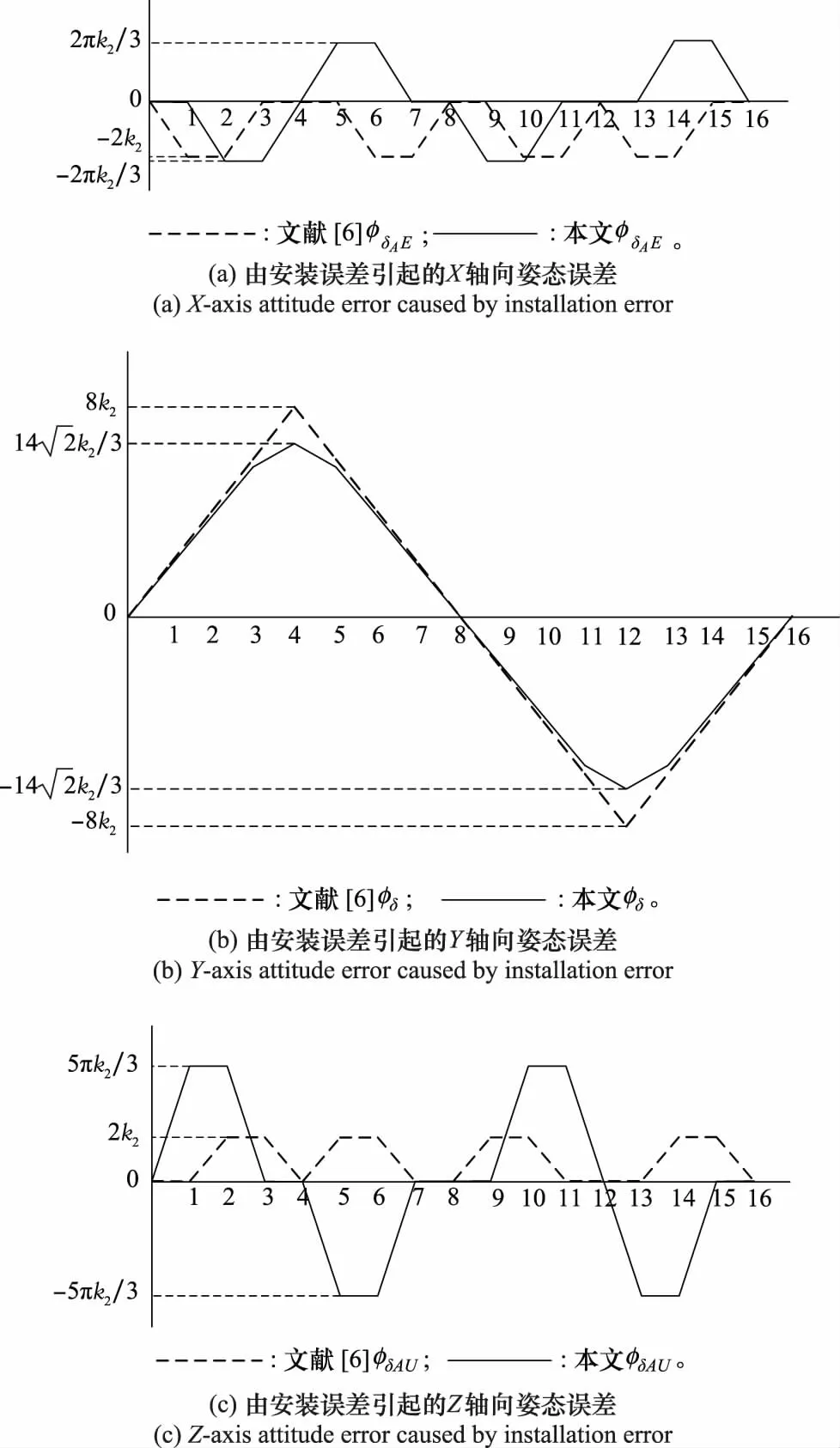
图4 由安装误差引起的姿态误差Fig.4 Attitude error caused by installation error

如图3所示,两种方案由刻度系数误差引起的姿态误差幅度变化一致,在北向轴上始终为零,东向轴和天向轴上的姿态误差被调制为零均值的周期形式,从而刻度系数误差不会出现积分并引起速度误差积累。

良好的课堂环境离不开师生的共同配合。教师的教学能够激发学生的学习兴趣，则课堂学习氛围好。要激发学生的学习兴趣，教师除了要有必备的学识，还要有良好的师德师风，具有人格魅力。而学生应多渠道加深对自己所学专业未来发展趋势的了解，挖掘所学专业的价值，发现学习的“有用性”，从而提升学习兴趣。[3]

3.2 速度误差分析

(13)

基于上文提到的载体静止预设,fn可以表示为

(14)

式中:g为当地重力加速度。

因此,可以得到东向速度误差和北向速度误差:

(15)

(16)

将式(11)和式(12)相加,求取由刻度系数误差和安装误差引起的姿态误差总和,并代入式(15)和式(16),可求得东向速度误差和北向速度误差。为了直观对比显示出两种方案的北向速度误差幅度大小,假设3组惯性器件的刻度系数误差相同,各轴向的安装误差相等。即设tr=π/ω,k12=k13=k21=k23=k31=k32=k2,k11=k22=k33=k1,简化后的北向速度误差如表4所示。

表4 两种方案的北向速度误差

从表4中可以看出,两种方案由刻度系数误差造成系统北向速度误差积累的幅值变化一致,本文方案的调制效果表现在抑制由安装误差造成系统速度误差的积累,如文献[6]中由安装误差引起的北向速度误差积累平均幅值为-9k2gtr,而本文方案平均幅值为(-2k2/3)gtr,在幅值大小方面本文方案的北向速度误差较小。

为了更清晰地显示本文北向速度误差幅值,将上述表格列写的由安装误差造成的北向速度误差累积幅度变化用折线图进行表示,如图5所示。

图5 北向速度误差幅度大小对比图Fig.5 Comparison diagram of error amplitude of northern velocity

数据处理结果表明:在本文提出的倾斜方案下,文献[6]的旋转调制方案能够更充分地减小由安装误差引起的北向速度误差累积,从而使位置误差得到充分调制。

忽略高度因素影响,位置误差方程为

(17)

(18)

式中:RM为子午圈曲率半径;RN为卯酉圈曲率半径。

由式(17)和式(18)可知,北向速度误差的减小导致纬度误差和经度误差减小。

4 仿真校验

为了验证本文所提出的倾斜方案的数学推导分析的正确性以及试验实际应用的效果,针对两种方案分别进行了刻度系数误差、安装误差和综合误差情况下的仿真实验。具体仿真参数设置如表5所示。

表5 仿真参数设置

4.1 刻度系数误差、安装误差仿真

为了验证上述关于由刻度系数误差和安装误差引起的姿态误差分析的正确性,分别设置仅有刻度系数误差和安装误差的两种仿真条件,验证姿态误差与图3和图4所述的幅值变化是否一致。

仿真条件仅包含刻度系数误差,具体数值如表5所示。实验结果如图6所示。图6为文献[6]旋转方案和本文旋转方案在一个周期内(960 s)由刻度系数误差引起的姿态误差对比,结合图3,两种方案由刻度系数误差引起的姿态误差幅度变化一致,所以如图6所示,本文旋转方案数据曲线将文献[6]方案覆盖。

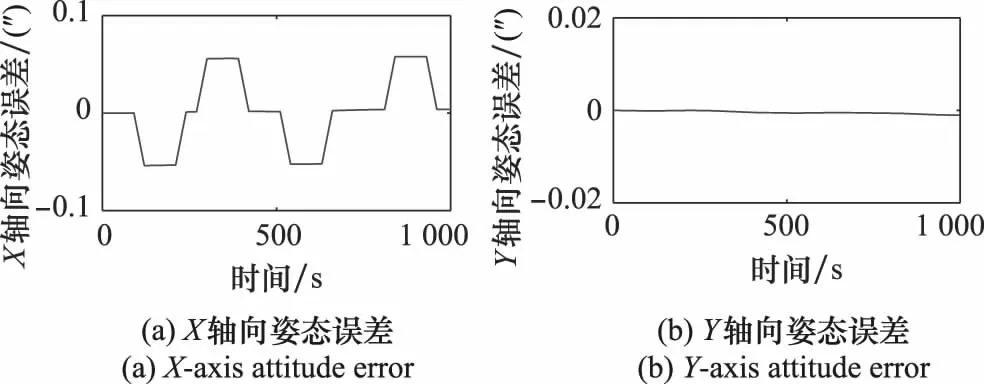
图6 由刻度系数误差引起的姿态误差对比图Fig.6 Comparison diagram of attitude errors caused by scale coefficient errors

仿真条件仅包含安装误差,具体数值如表5所示(见前页)。图7为两种旋转方案由安装误差引起的姿态误差对比图。从图7可以看出,本文旋转方案不仅可以将北向轴姿态误差调制为零均值的周期形式,而且还可以将东向轴和天向轴姿态误差调制为零均值周期形式。因此,验证了表3和图3中数学推导的正确性。

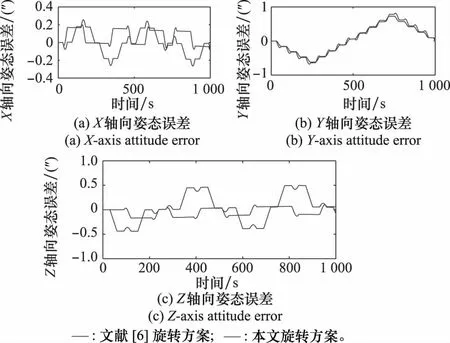
图7 由安装误差引起的姿态误差对比图Fig.7 Comparison diagram of attitude errors caused by installation errors

为了验证上述速度误差数学推导的正确性,实验仿真条件仅包含安装误差。实验结果如图8所示,本文方案相较于文献[6]方案速度误差显著减小,变化趋势与图5一致。

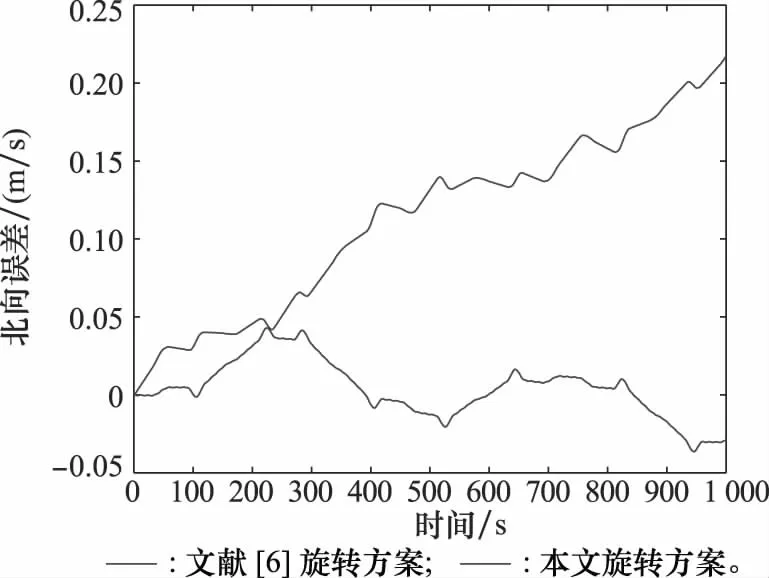
图8 由刻度系数误差和安装误差引起的北向速度误差对比Fig.8 Comparison diagram of north velocity error caused by scale coefficient error and installation error

4.2 综合误差仿真

为了试验本文方案在实际应用中的效果,在此设置实际应用中存在的主要误差源,进行综合误差仿真,参数设置如表5所示。

一个周期内(960 s)由综合误差引起的姿态误差和速度误差如图9和图10所示。

图9 一个周期内x轴、y轴姿态误差对比图Fig.9 Comparison diagram of x-axis and y-axis attitude errors in one cycle

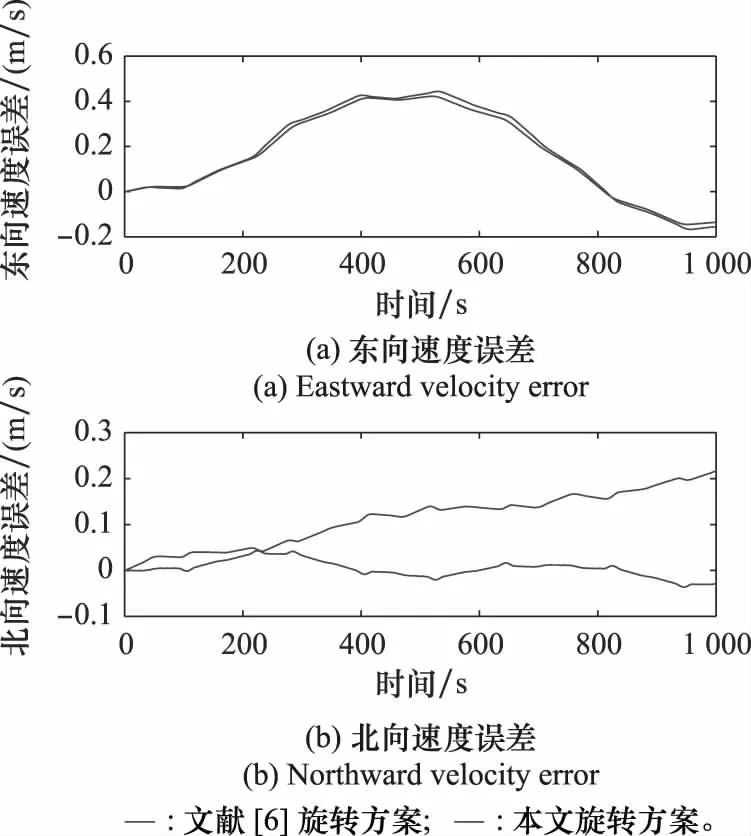
图10 一个周期内东向、北向速度误差对比图Fig.10 Comparison diagram of eastward and northward velocity errors in one cycle

长航时(120 h)内由综合误差引起的姿态误差、速度误差以及位置误差如图11～图13所示。

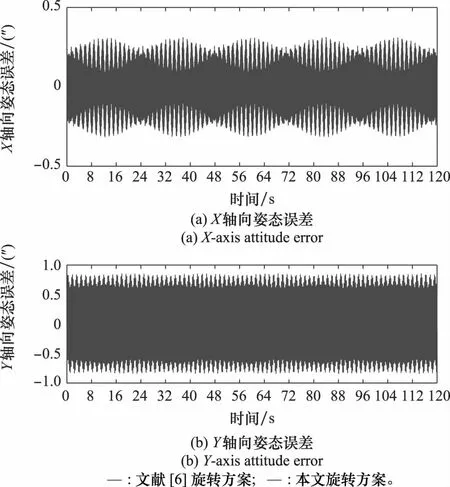
图11 长航时(5天)x轴、y轴姿态误差对比图Fig.11 Comparison diagram of x-axis and y-axis attitude errors in five days

图12 长航时(5天)东向、北向速度误差对比图Fig.12 Comparison diagram of eastward and northward velocity errors in five days

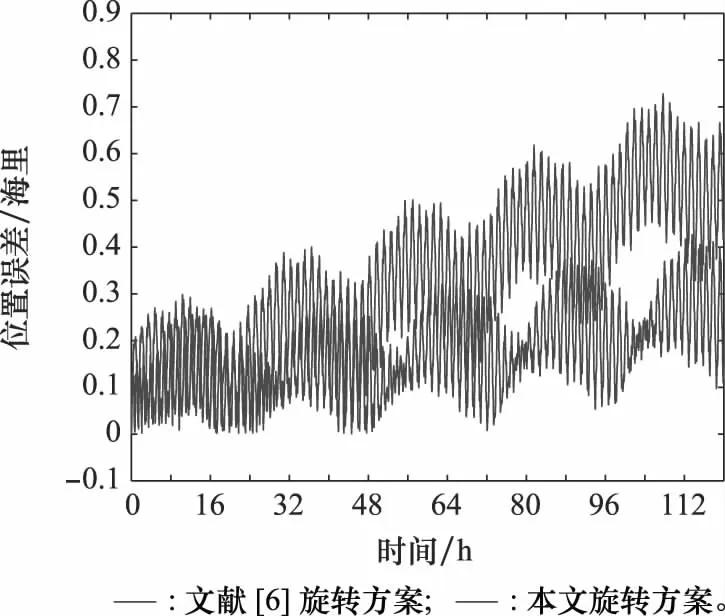
图13 长航时(5天)位置误差对比图Fig.13 Comparison diagram of position errors in a five days

如图9、图10所示,与文献[6]方案相比,在本文方案将x轴姿态误差调制为零均值的周期形式,结合表4,本文方案对系统x轴向姿态误差的调制效果主要体现在对安装误差的调制作用。因此,北向速度误差累积相应减小。本文方案在y轴向姿态误差幅度抑制能力与文献[6]方案相近,所以东向速度误差累积幅度减小不明显。因此,图9和图10进一步充分证明了上述理论推导的正确性。

由式(17)和式(18)以及上述分析,相较于文献[6]方案,在本文方案旋转调制下,系统北向速度误差减小,从而位置误差相应减小,如图13所示。本文方案的位置误差从文献[6]方案的0.418 9海里/120小时减小到0.120 7海里/120小时。

5 结 论

旋转调制惯性导航系统的误差补偿取决于旋转方案的设置。与传统旋转方案不同,本文采用IMU基于体对角线旋转的方式,不仅没有引入新的误差,而且使各种误差相对减小,特别是对安装误差的调制效果明显。在综合误差条件下,本文提出的基于IMU体对角线的旋转方案将文献[6]中的位置误差从0.418 9海里/120小时减小到0.120 7海里/120小时,达到了一定的误差抑制效果。