基于态势演化博弈的无人机集群动态攻防

盛 磊, 时满红, 亓迎川,*, 李 浩, 庞明军

(1. 空军预警学院, 湖北 武汉 430000; 2. 中国人民解放军95894部队, 北京 100000)

0 引 言

无人机在军事和民用领域都有广泛的应用[1-3],在复杂条件下,可以替代有人机执行“枯燥、恶劣、危险、纵深(dull, dirty, dangerous and deep, 4D)”任务[4]。随着人工智能(artificial intelligence, AI)技术的发展,集群控制成为无人机应用的发展方向[5]。无人机集群作战[6-8]也成为无人机军事应用的研究热点。

现阶段无人机集群动态攻防的研究仍处于初步阶段,实现的方法主要包括:基于专家系统和基于博弈论。

基于专家系统[9]的规则制定,就是通过总结以往空战经验,设计态势评估函数,针对障碍物或者敌我态势,己方选择相应行为准则。文献[10]设计了一种自组织的攻防对抗决策(offense-defense confrontation decision-making, ODCDM)算法,利用分布式决策,通过与邻近友机的通信,完成态势感知,求解控制输入,实现无人机集群的对抗。文献[11]提出了一种将模糊专家系统与差分进化算法相结合的逃逸机动决策算法,通过以往战术知识的学习,建立模糊专家系统,根据模糊专家系统实现机动动作的选择,而后经过差分算法寻优,最后完成对机动动作的最优控制。Yang[12]等利用深度Q网络(deep Q network,DQN)搭建了无人机决策模型,计算敌我双机对抗过程中的态势变化,根据机动动作库中相应规则,完成无人机决策。

虽然基于专家系统的无人机集群算法能够有效且稳定地解决无人机集群对抗问题,但是其依赖于专家库的建立,处于不确定环境或者集群规模过大时,存在调试时间长,策略选择不是最优等不足。

基于博弈论[13-16]的方法,就是一类研究智能体之间策略交互的数学理论与方法[17]。相比专家系统,该方法不需要先验知识,可以通过自学习逐步获得最优策略。文献[18]提出了一种基于演化博弈框架下的多智能体策略竞争,设立了合作、惩罚、投机以及孤立4种策略,通过初始条件的变化,验证了多智能体运动的演进方向。文献[19]基于捕食猎物粒子群优化(predator-prey particle swarm optimization, PP-PSO)的博弈论方法,将攻防对抗中的复杂任务分配转化为每阶段的双方博弈,然后利用PP-PSO求解与之对应的纳什均衡,保证攻防双方在对抗过程中采取对己方最有利的策略。文献[20]基于竞争学习鸽群优化(competitive learning pigeon-inspired optimization, CLPIO)算法,采用分布式群对抗方式,分别设计了两种动态博弈模型:仿鹰的攻击子群和仿鸽的对抗子群,利用CLPIO算法寻找混合纳什均衡。文献[21]利用多人动态博弈分解解决多无人机追逃问题,降低了时间复杂度,提升了运行速度。但是,这些基于博弈论的无人机集群攻防对抗,在涉及基地概念时,多数将其作为目标点,基地并不具备功能,这与实际情况存在差异。

本文结合专家系统和演化博弈的优点,提出了态势演化博弈模型。贴近实际作战场景,赋予基地探测功能,基地能够提高守方无人机的态势感知能力,并且能够与守方无人机集群保持通信。在此基础上,构造了基地-守方无人机集群-攻方无人机集群三者相互影响的攻防情形。首先,分别设计了攻方无人机态势评估函数、守方无人机态势评估函数和基地态势评估函数,切实体现对抗过程中攻防双方的态势变化情况。然后,将各阶段态势变化,代入演化博弈模型,使每一阶段的演化博弈过程延伸到全阶段全员的博弈,并使攻防双方在各阶段都处于演化稳定状态(evolutionary stable state, ESS),实现攻防双方无人机集群对抗策略的自适应最优选择。

1 双方无人机集群动态描述

双方无人机集群的动态描述包括无人机集群动态攻防场景与规则、基地生存模型、无人机单机攻防模型和无人机集群攻防模型。其中,无人机动态攻防场景与规则给定了攻防对抗的作战背景以及双方的胜负条件;基地的生存模型,主要表现基地受攻防双方无人机集群的影响,其生存率的变化情况;无人机单机攻防模型,主要体现无人机单机的运动准则及武器数量的变化;无人机集群攻防模型,主要体现集群运动规则以及控制输入随策略选择的变化情况。

1.1 无人机集群动态攻防场景与规则

双方无人机性能相同,携带武器的功能与数量相同。模拟场景假定为,不考虑高度因素,双方处于同一二维区域。攻方无人机已知基地位置,在一定的时间窗口,经过奔袭,对守方发动进攻。守方无人机集群在对抗开始前,采取巡航方式对基地进行有效防卫,且基地具备一定的探测能力,能与守方无人机集群建立持续有效的通信,在基地探测范围内,能够提升守方无人机的态势感知能力。当双方武器消耗殆尽时,攻方无人机会选择撤离,守方无人机会选择回到基地。

攻守布防示意图如图1所示。

图1 攻守布防示意图Fig.1 Offensive and defensive deployment diagram

攻方为达到进攻效益最大化,采取整体分散,局部聚集的策略;在未探测到攻方无人机时,守方无人机在基地受威胁区与基地探测区之间巡航。所谓基地受威胁区,就是以基地为中心,无人机攻击距离为半径的圆;所谓基地探测区,就是以基地为中心,基地探测距离为半径的圆。

在攻防对抗的时间窗口内,双方的胜负条件为:① 基地生存率小于被瘫痪阈值Ph,则攻方胜利;② 基地生存率大于被瘫痪阈值Ph,则守方胜利。

为简便分析,将无人机模型视为质点,并假设:① 无人机能够准确进行敌我识别,且每一时刻只针对敌方单一目标发动攻击;② 无人机能够探知友机的位置等信息;③ 无人机能够探知敌机的速度、方位、位置等信息。

1.2 基地生存模型

影响基地生存率的因素包括攻方无人机对基地的毁伤以及守方无人机采取防御策略时为基地带来的收益。基地的生存率模型为

pb(t+1)=pb(t)·Ab(t)

(1)

(2)

(3)

式中:t表示作战时刻;pb(t)表示t时刻基地的生存率;Ab(t)表示基地从t时刻到t+1时刻生存率;pib(t)表示t时刻攻方第i架无人机对基地的毁伤概率;nib(t)表示t时刻攻方第i架无人机对基地发射的武器数;β(0≤β≤1)为环境影响因素;Sib(t)表示t时刻攻方第i架无人机攻击基地时对基地的态势优势;Sjb(t)表示t时刻守方第j架无人机采取防御策略时为基地带来的态势优势;nDO为t时刻针对攻方第i架无人机采取防御策略的守方无人机数目;Kib表示武器对基地的理想杀伤概率,规定Sib(t)-Sjb(t)≥0。

设定基地瘫痪阈值为Ph=0.4,当基地的生存率小于基地存活阈值时,认为基地被摧毁。

1.3 无人机单机攻防模型

每架无人机的状态矩阵为

(4)

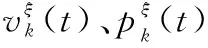
每架无人机的状态方程为

(5)

(6)

(7)

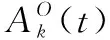
(8)

(9)

在t时刻,攻方第k架无人机发射的武器数为攻击守方无人机与攻击基地的数目的和,即

(10)

同理,守方第k架无人机发射的武器数为攻击攻方无人机的数目,即

(11)

(12)

(13)

(14)

设定无人机生存阈值为PT,当无人机的存活率小于无人机生存阈值时,认为该无人机被摧毁。

1.4 无人机集群攻防模型

常见的集群运动模型包括:Vicsek模型[22-23]、Couzin模型[24]以及社会力模型[25]。社会力模型是基于牛顿力学的建模方式,将个体间的协同,抽象为力的形式,能直观体现双方无人机集群的动态运动。

本文采用自下而上的基于个体的建模方式,通过个体运动的拉格朗日法,建立无人机集群的动力学模型,对于具有N个个体的群运动,群中个体i的拉格朗日模型为

(15)

集群运动的3个基本规则为分离、聚集和速度一致。在此基础上,针对双方无人机集群的对抗,本文又增加了进攻、防守与防御3项攻防规则。

(1) 分离准则

所谓分离,就是集群运动时,避免群内个体发生碰撞,相邻个体间产生斥力作用。

(16)

(2) 聚集准则

所谓聚集,就是在无人机探测范围内,群内个体相互靠近,相邻个体间产生引力。

(17)

分离和聚集规则,构成了集群运动的位置协同力,由位置关系产生的总力为

(18)

式中:a,b,c为常数,构建的目的是当无人机i与相邻友机距离过近时,相互排斥;当无人机i与相邻友机距离过远时,相互吸引。无人机间相互作用,在位置上形成群的形式,刻画个体间的防撞和空间的聚集特性。

(3) 速度一致性准则

所谓速度一致性,就是速度协同力,使群内个体保持速度一致。

(19)

(4) 攻击准则

攻方无人机的防守策略和守方无人机的出击策略,是彼此之间的攻击,因此两者采用相同的准则。

(20)

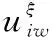
(5) 进攻准则

进攻准则就是攻方无人机向基地发动攻击的行为准则。

(21)

式中:kb为常数,是控制增益;uib为攻方第i架无人机对基地发起进攻时,其向基地运动的力。

(6) 防御准则

守方采取防御策略,最佳情况就是与基地保持适当距离,一旦探测到攻方无人机,保证守方无人机有充足的时间做出反应。

(22)

综上,攻方无人机会采用策略式(1)～式(5),即攻方无人机的总输入为

(23)

(24)

守方无人机会采用策略式(1)～式(4)和式(6),即守方无人机的总输入为

(25)

(26)

2 态势演化博弈模型

2.1 态势评估函数

态势评估[26-28]函数包括双方无人机的态势优势评估,以及基地与双方无人机间态势的相互影响。

2.1.1 双方无人机间的态势评估

某时刻,双方无人机对抗关系如图2所示。

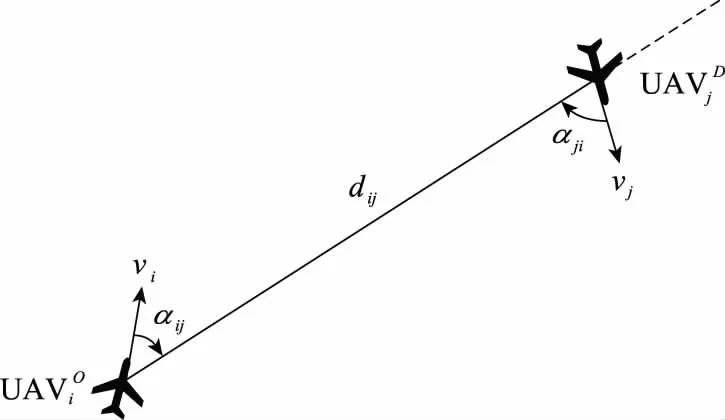
图2 双方无人机对抗方位图Fig.2 Azimuth map of unmanned aerial vehicle confrontation between both sides

影响无人机间态势评估函数的因素主要包括角度、速度以及距离。

(1) 角度优势函数

(27)

随着方位角的增加,角度优势呈非线性减小,即追击式的攻击会带来最大的角度优势。

(2) 速度优势函数

(28)

无人机间的相对速度越大,速度优势越明显。

(3) 距离优势函数

(29)

式中:dij为无人机间距离;rs为无人机探测距离。

随着无人机间的距离减小,距离优势函数呈线性增大。

上述3种优势函数,综合影响无人机间的态势评估,根据三者影响权重的不同,无人机间总的态势评估函数为

Sij=ω1Sαij+ω2Svij+ω3Srij

(30)

2.1.2 无人机与基地的态势评估

某时刻,无人机与基地对抗关系如图3所示。

图3 无人机与基地对抗方位图Fig.3 Azimuth map of unmanned aerial vehicle and base confrontation

(1) 攻方无人机与基地的态势评估函数

影响攻方无人机与基地态势评估函数的因素主要包括角度和距离。

角度优势函数:

(31)

即只有当攻方无人机向基地方向运动时,才会存在角度优势,该优势随着方位角的增加呈非线性减小。

距离优势函数:

(32)

随着无人机与基地的距离减小,距离优势呈线性增大。

上述两种优势函数,综合影响攻方无人机与基地间的态势评估,根据两者影响权重的不同,攻方无人机与基地间总的态势评估函数为

(33)

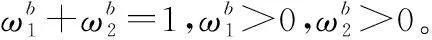
(2) 守方无人机与基地的态势评估函数

当守方无人机采取防御策略时,与基地相互作用,两者越近,基地为守方无人机带来的态势感知优势越明显;守方无人机越靠近基地,越能提高基地的生存概率。

守方无人机为基地带来的态势优势:

(34)

式中:rb为基地探测距离;djb为守方无人机与基地的距离。

守方无人机与基地的距离越小,守方无人机为基地带来的态势优势越大。

基地为守方无人机带来的态势优势:

(35)

基地与守方无人机的距离越小,基地为守方无人机带来的态势优势越大。

2.2 演化博弈分析

演化博弈模型[29-30]的优势是,既可以直观有效地解决博弈主体的行为选择,也可以出于利益最大化原则,体现双方攻防对抗的动态变化。

2.2.1 模型假设

本次博弈的主体为:攻方无人机和守方无人机。攻方无人机的策略集为{进攻,防守};守方无人机的策略集为{出击,防御}。具体定义如下。

攻方无人机的策略:① 进攻,即直接对基地发起进攻;② 防守,即直接与守方无人机进行对抗。

守方无人机的策略:① 出击,即在基地探测区外,主动对攻方无人机发动进攻;② 防御,即守方无人机在基地探测区域内与攻方无人机展开对抗。

攻方无人机对守方发动袭击,会产生燃油消耗、资源占用等成本Ci;攻方无人机选择进攻时,直接威胁基地,为攻方带来收益G1的同时,基地承担的风险,也以π1G1(0≤π1≤1)的方式影响守方无人机的收益;攻方无人机选择防守时,通过摧毁守方无人机,增加攻方无人机数目和能力优势,为攻方带来收益G2。

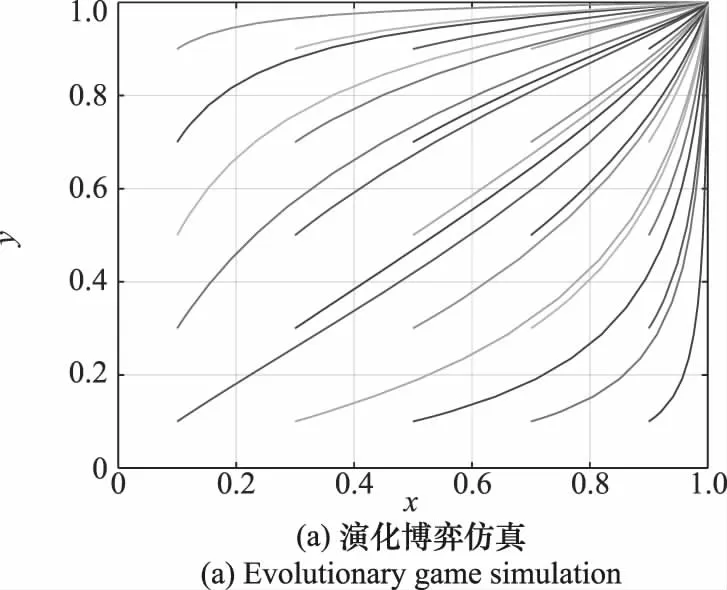
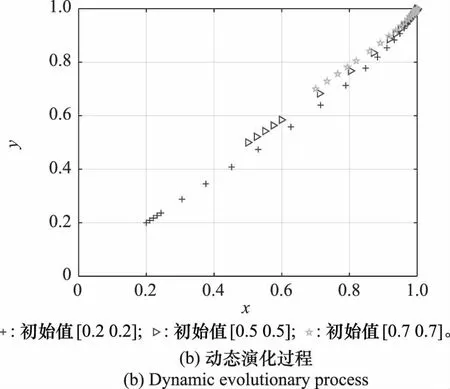
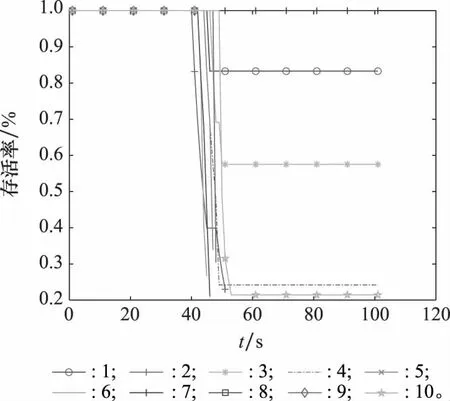
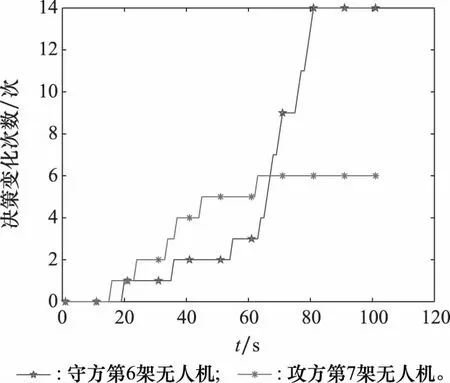
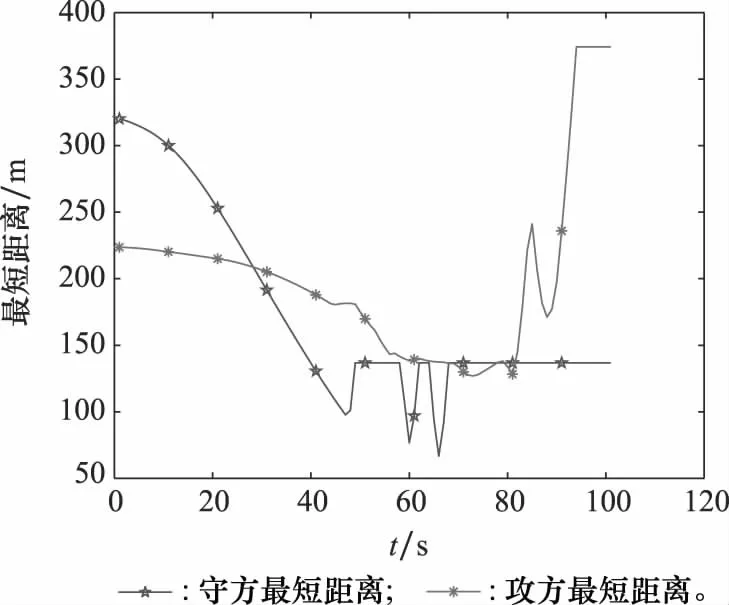
守方无人机前期进行巡航侦察,同样会产生燃油消耗、资源占用等成本Cj,由于守方无人机在基地附近巡航,不需要远距离奔袭,所以产生成本较小,即Cj

基地具备探测功能,能够提高守方无人机的态势感知优势,理想状态下会为守方无人机带来收益B3,随着基地生存率π3的变化,该收益也会发生变化。

攻方无人机发动进攻的概率为x,进行防守的概率为1-x;守方无人机进行出击的概率为y,进行防御的概率为1-y。

2.2.2 模型构建

根据模型假设,攻方无人机与守方无人机的收益矩阵如表1所示。

表1 态势演化博弈收益矩阵

结合表1的收益矩阵,设攻方无人机选择进攻的期望收益为E11,选择防守的期望收益为E12,攻方无人机的平均期望收益为E1。

E11=y(G1-Ci-B1)+(1-y)(G1-Ci-B2-π3B3)

(36)

E12=y(G2-Ci-B1)+(1-y)(G2-Ci-B2-π3B3)

(37)

E1=xE11+(1-x)E12

(38)

根据式(36)～式(38)可以得到攻方无人机的复制动态方程:

(39)

同理,设守方无人机选择出击的期望收益为E21,选择防御的期望收益为E22,守方无人机的平均收益为E2。

E21=x(B1-Cj-π1G1)+(1-x)(B1-Cj-G2)

(40)

E22=x(B2-Cj-π1G1+π2R+π3B3)+
(1-x)(B2-Cj-G2+π2R+π3B3)

(41)

E2=yE21+(1-y)E22

(42)

根据式(40)～式(42)可以得到守方无人机的复制动态方程:

(43)

2.2.3 演化博弈分析

由F(x)=F(y)=0,可得到4个均衡点如表2所示。

表2 均衡点

根据Friedman的研究方法,利用Jacobian矩阵的局部稳定性可以对这4个复制动态均衡点的稳定性进行分析,通过对F(x)与F(y)求偏导可得Jacobian矩阵为

根据演化博弈理论知识可知,只有满足det(J)>0且tr(J)<0的均衡点才会趋于稳定。各均衡点的稳定性分析如表3所示。

表3 各均衡点矩阵行列式和迹的表达式

2.2.4 攻防双方策略的选取

(1) 均衡点1的渐进稳定条件

均衡点1的渐进稳定条件如下:

对均衡点1的仿真结果如图4所示。图4中,横坐标代表攻方无人机选择进攻策略的概率,纵坐标代表守方无人机选择出击策略的概率。

即在此条件下,攻方无人机选择防守策略,守方无人机选择防御策略。

(2) 均衡点2的渐进稳定条件

均衡点2的渐进稳定条件如下:

对均衡点2的仿真结果如图5所示。

图5 均衡点2Fig.5 Equilibrium point 2

即在此条件下,攻方无人机选择进攻策略,守方无人机选择防御策略。

(3) 均衡点3的渐进稳定条件

均衡点3的渐进稳定条件如下:

对均衡点3的仿真结果如图6所示。

图6 均衡点3Fig.6 Equilibrium point 3

即在此条件下,攻方无人机选择防守策略,守方无人机选择出击策略。

(4) 均衡点4的渐进稳定条件

均衡点4的渐进稳定条件如下:

对均衡点4的仿真结果如图7所示。

图7 均衡点4Fig.7 Equilibrium point 4

即在此条件下,攻方无人机选择进攻策略,守方无人机选择出击策略。

2.3 态势演化博弈模型的实现

态势评估函数与演化博弈模型相结合,将某一时刻态势评估函数的值作为演化博弈模型的数据。在无人机的探测范围内,首先,利用态势评估函数,遍历自身对敌方无人机的优势。然后,依据演化博弈模型中选择策略的条件,实现双方无人机的自适应策略选择。最后,将每一阶段的态势评估函数数值以及无人机状态带入相应模型,完成全阶段态势演化博弈的策略选择和全员的实时状态更新,保证了每一阶段每一架次的策略选择都处于纳什均衡,即做出了对己方最有利的策略选择和状态变化。

态势演化博弈模型与态势评估函数的对应关系如表4所示。

表4 博弈论模型与态势评估函数的对应关系

当出现一架无人机对敌方多架无人机采取相同策略时,攻方无人机以G2的大小确定优先级顺序,G2越大越优先,G2相同时再按照态势评估函数的权重比进行优先级排序,即权重越大的态势评估函数,其值越大,则优先级越高。防守无人机的策略选择以态势评估函数的权重比进行判断。

3 仿真与实验

3.1 参数设定

本实验采用Matlab R2021b编写仿真程序。无人机与基地参数如表5所示,无人机集群动态对抗模型参数如表6所示。

表5 无人机与基地参数

表6 无人机集群动态对抗模型参数

3.2 仿真结果与分析

基地坐标为(0,7 500),攻方无人机经过突袭,在距离基地12～15 km处发起攻击。仿真结果如图8所示。

图8 无人机集群攻防轨迹Fig.8 Unmanned aerial vehicle swarm offensive and defensive trajectory

图8中,以基地为中心的小圆代表基地的受威胁区,当攻方无人机携带武器进入此区域时,会给基地带来一定的威胁。以基地为中心的大圆代表基地的探测区。每20 s为攻防双方的轨迹做一个标记。其中,代表攻方无人机的蓝色三角形反向时,表明此时武器消耗殆尽,攻方无人机撤离;代表守方无人机的红色三角形反向时,表明守方无人机策略的改变,由出击转为防御,不再远离基地,而是向基地方向回防。

从图8中可以看出,攻方无人机最初采取进攻策略,以编队方式向基地前进;守方无人机最初采取防御策略,在基地受威胁区与基地探测区间巡航。最终双方相遇,初始相遇阶段,攻方具备先发优势:守方无人机对最接近基地探测区的攻方无人机进行拦截,以使得守方优势最大化,这给后续分散到达的攻方无人机可乘之机,故而双方遭遇的初始阶段,守方无人机处于劣势。随着时间的推移,基地的作用凸显,守方处于优势:攻方无人机逐渐进入到基地的探测区内,此时基地为守方无人机增强了态势感知能力,守方无人机与攻方无人机在此范围内对抗,消耗了攻方无人机的武器数量,增加了基地的生存率。双方无人机对抗的最后阶段:双方武器消耗殆尽,攻方选择撤离,守方无人机或大角度机动,或缓慢机动,由出击策略变为防御策略,返回基地。

图9显示了双方无人机剩余数量随时间变化的情况,在45～49 s,双方最初遭遇,此时即攻方优势期,守方迅速损失4架。而后,双方进入相持阶段,彼此纠缠,在50～70 s,双方数量基本保持不变;在75～85 s,随着攻方无人机的持续深入,基地功能凸显,逐步进入到守方优势期,攻方无人机数目渐次减少;85 s之后,为对抗结束期,双方武器消耗殆尽,改变策略,各自撤离战场。

图9 双方无人机剩余数量图Fig.9 Number of remaining unmanned aerial vehicles on both sides

为更直观体现双方无人机的动态攻防过程,双方无人机的存活率分别如图10和图11所示,可以看到任一架无人机任意时刻被攻击的情况。其中,不连续的线,表示下一时刻该无人机的存活率低于生存阈值,即被击毁。

图10 攻方无人机剩余数量图Fig.10 Number of remaining unmanned aerial vehicles on offensive side

图11 守方无人机剩余数量图Fig.11 Number of remaining unmanned aerial vehicles on defensive side

图12和图13中显示了双方无人机剩余武器数目随时间的变化。

图12 攻方无人机武器剩余数量图Fig.12 Number of offensive unmanned aerial vehicles’weapons remaining

图13 守方无人机武器剩余数量图Fig.13 Number of defensive unmanned aerial vehicles’weapons remaining

由以上分析可知,在成规模的无人机集群对抗仿真中,基地安好,守方胜利。为更直接展现无人机集群对抗中无人机个体的策略选择,选取攻方第7架无人机和守方第6架无人机进行分析,两者策略变化如图14所示。

图14 所选无人机决策结果图Fig.14 Decision results of the selected unmanned aerial vehicles

图14中曲线的每一次突变,代表策略的变化。在未发生对抗前,即15 s时,攻方率先改变策略,对守方无人机发动进攻,体现了攻方的前期先发优势。守方迎战,策略变化慢于攻方,随着态势逐渐对守方有利,守方策略转化明显,即态势占优时攻击,击毁攻方无人机后,短时间无合适目标,选择防御策略,随着位置变化,又发现其他攻方无人机,进而策略不断变化。当双方武器消耗殆尽后,策略不再改变。图14说明,攻防双方的策略可以随着态势变化而自适应选择。

由图15的无人机间最小距离图可知,在集群攻防过程中安全可控,没有发生碰撞。守方无人机在对抗初始阶段的最短距离迅速变小,与之前分析相符。为了验证具备探测功能的基地对攻防双方胜负的影响,利用蒙特卡罗法分别进行1 000次仿真实验,基地具备探测功能时,攻方胜利次数:守方胜利次数为367:633;基地不具备探测功能时,攻方胜利次数:守方胜利次数为507∶493。即具备探测功能的基地为守方提高了14%的胜率。

图15 所选无人机决策图Fig.15 Selected unmanned aerial vehicles decision map

4 结束语

本文提出的态势演化博弈模型,能够解决基地具备功能情况下的攻防双方无人机集群协同对抗的自适应。无人机个体能够根据自身态势情况,选择最优策略,实现自身收益最大化。运用该模型,使无人机集群对抗展现出强大的对抗能力,仿真实验证明了基地具备探测功能时能够有效提高守方胜率。

下一步将拓展无人机和基地功能,实现攻防双方在三维空间上的集群动态对抗。