主瓣掩护式干扰背景下单脉冲雷达角度估计

王 磊, 张启亮, 翁明善

(1. 空军工程大学防空反导学院, 陕西 西安 710051; 2. 中国人民解放军93688部队, 天津 300202;3. 中国人民解放军93159部队, 辽宁 大连 116033)

0 引 言

单脉冲技术具有测角精度高、抗干扰能力强的特点,已经被广泛应用于现代雷达系统中[1-3]。随着电子战技术的不断发展,单脉冲雷达面临的电磁环境日益复杂,主瓣掩护式干扰是雷达主瓣干扰中一种较为常见的形式。这种干扰通常由敌方用于掩护战斗机飞行的干扰机施放,经雷达方向图主瓣进入接收机,并与目标之间保持一个非常小的夹角,该夹角通常小于雷达半功率波束宽度[4]。传统的用于对抗旁瓣干扰的低副瓣天线[5-6]、旁瓣对消[7-12](side lobe cancellation, SLC)、旁瓣匿影[13-15](side lobe blanking, SLB)等技术无法继续生效,并且由于干扰与目标夹角较小,常规自适应波束形成(adaptive beam forming, ABF)技术在干扰角度形成的零陷会使目标信号损失严重,导致单脉冲雷达的探测性能严重下降[16]。因此,如何在主瓣掩护式干扰背景下进行角度估计,是单脉冲雷达面临的经典问题。

Yu等[17]将旁瓣相消自适应阵列与主瓣干扰相消器进行级联,能够同时抑制主瓣干扰与副瓣干扰。胡航等[18]将该方法应用到子阵级中,但该方法依赖于主瓣干扰的精确信息,不容易实现。文献[19]提出了一种子阵间约束自适应和差单脉冲测角算法,能够在抑制主瓣与副瓣干扰的同时保持单脉冲比,提高测角精度,但该方法在主瓣干扰附近的测角精度较低。文献[20]采用分维的方法,在一个维度上进行MLC,在另一维度上进行目标角度测量,从而提高了单脉冲的测角性能。

针对主瓣干扰,目前的空域抗干扰技术[17-24]主要出发点是采取对消的方式,为避免主波束变形,通常需要采用主瓣保形技术,并且这些抗干扰技术依赖于对主瓣干扰角度的精确估计,这无疑增加了系统的复杂程度与工程实现难度。以频率分集阵为代表的波形分集阵列雷达,可以通过调制发射端使其具有额外距离维自由度,增加了系统设计与信号处理的灵活性,改变了传统雷达获取信息的方式,为解决主瓣干扰抑制难题提供了新的思路,是雷达技术创新的重要途径[25-26]。但该技术主要应用于新体制雷达,传统单脉冲体制雷达无法应用该技术。针对这些问题,本文基于单脉冲雷达提出了一种主瓣掩护式干扰背景下目标角度估计算法,该算法通过对接收到的信号进行处理,能够在主瓣掩护式干扰背景下较为准确地估计目标角度。

1 相关背景

1.1 一维单脉冲天线波束形成

假设一个N阵元,阵元间距为半波长的一维均匀线性阵列,其在θ方向的导向矢量可表示为

aθ,N=[1,ejπsin θ,…,ej(N-1)πsin θ]T

(1)

该天线在目标方向θp上的和、差波束形成器可表示为

wΣθp,N=aθp,N∘wT,N

(2)

wΔθp,N=aθp,N∘wB,N

(3)

式中:“∘”表示两个向量之间的Hadamard积;wT,N、wB,N分别表示Taylor窗向量与Bayliss窗向量[27-28];元素个数为N。

形成的和、差波束在方向θ上的天线增益分别为

(4)

(5)

由式(4)和式(5)可得一维均匀线性单脉冲角度鉴别函数:

(6)

1.2 二维单脉冲天线波束形成

对于纵向、横向阵元个数分别为Ne、Na,阵元间距为半波长的二维平面阵列,其在俯仰角θe、方位角θa方向上的导向矢量可以表示为

νθe,θa=aθe,Ne⊗aθa,Na

(7)

式中:“⊗”表示Kronecker积。

单脉冲轴线指向为俯仰角θep、方位角θap,和波束、俯仰差波束、方位差波束、双差波束的波束形成器可分别表示为

wΣ=wΣθep,Ne⊗wΣθap,Na

(8)

wΔe=wΔθep,Ne⊗wΣθap,Na

(9)

wΔa=wΣθep,Ne⊗wΔθap,Na

(10)

wΔΔ=wΔθep,Ne⊗wΔθap,Na

(11)

形成的波束在俯仰角θe、方位角θa方向上的增益可分解为对应的一维俯仰、一维方位单脉冲天线增益的乘积形式,分别为

(12)

(13)

(14)

(15)

由式(12)～式(15)可得二维单脉冲天线的角度鉴别曲线

(16)

(17)

1.3 二维单脉冲网络MLC原理

假设目标信号st的来向为俯仰角θet、方位角θat,主瓣干扰信号sj的来向为俯仰角θej、方位角θaj,此时单脉冲系统4个通道输出的目标、干扰与噪声的混合信号可分别表示为

xΣ=gΣ(θej,θaj)sj+gΣ(θet,θat)st+nΣ

(18)

xΔe=gΔe(θej,θaj)sj+gΔe(θet,θat)st+nΔe

(19)

xΔa=gΔa(θej,θaj)sj+gΔa(θet,θat)st+nΔa

(20)

xΔΔ=gΔΔ(θej,θaj)sj+gΔΔ(θet,θat)st+nΔΔ

(21)

式中:xΣ、xΔe、xΔa、xΔΔ分别表示和通道、俯仰差通道、方位差通道以及双差通道的输出信号;nΣ、nΔe、nΔa、nΔΔ分别表示和通道、俯仰差通道、方位差通道以及双差通道的噪声信号。

主瓣干扰会导致二维单脉冲角度鉴别曲线与静态鉴角曲线失配,使得角度估计性能严重下降。为了抑制主瓣干扰并能够保持单脉冲鉴角曲线,学者提出了单脉冲天线波束间MLC技术,图1为该算法的工作原理[17,29-30]。

图1 单脉冲天线波束间MLC技术Fig.1 MLC technique between monopulse antenna beams

二维单脉冲天线接收目标信号,各通道的输出信号经过MLC后的信号可分别表示为

(22)

(23)

(24)

(25)

其中[17,31]

(26)

(27)

经过MLC后,目标角度由下式确定:

(28)

(29)

2 本文算法原理

2.1 信号模型

对于纵向、横向阵元个数分别为Ne、Na的四通道单脉冲雷达,设定目标回波点数为M,则单脉冲天线接收信号模型可表示为

(30)

其中,

(31)

为和通道、俯仰差通道、方位差通道以及双差通道对干扰与目标信号的增益所组成的干扰及目标信号增益矩阵。

(32)

为干扰及目标信号矩阵;

(33)

为接收机噪声矩阵。

为方便表示,记:

(34)

其中,

(35)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

(46)

2.2 干扰信号来向估计

对于实际的单脉冲系统,可以通过测量得到接收信号X,由于干扰处于雷达主瓣范围内,各通道内的干扰信号功率远远大于目标信号与接收机噪声功率,各通道内的接收信号功率趋近于干扰信号功率。因此,干扰信号来向可以通过求取接收信号X的差和比获得。

俯仰差通道与和通道的差和比为

(47)

其估计值为

(48)

令:

ξ=(wΔexΣj-xΔej)(wΔexΣj-xΔej)H=

(49)

(50)

其中“(·)*”表示共轭复数。

(51)

同理,方位差通道与和通道的差和比估计值为

(52)

双差通道与和通道的差和比估计值为

(53)

从而可以估计出干扰信号来向。

2.3 目标角度估计

为了对目标回波信号进行提取,建立如下优化模型:

(54)

由于噪声信号功率远远小于目标与干扰信号功率之和,故该模型通过计算残差矩阵的F-范数获得目标及干扰信号的最优估计,当F-范数取最小值时,残差信号功率最小,则此时可得到目标及干扰信号的最优估计。

通过干扰信号来向可求取干扰、目标信号增益矩阵A中各通道的干扰信号增益。由于本文只需应用到各通道信号的增益比,故用干扰信号的归一化增益替代干扰信号增益,令:

gΣj=1

(55)

由式(47)、式(51)可得:

(56)

同理,

(57)

(58)

为确定A中各通道的目标信号增益,以3 dB波束宽度为目标回波来向θΔet、θΔat的搜索范围,并在搜索范围内分别等间隔取m与n个点,即:

θΔetm=θΔet0+mΔθΔet

(59)

θΔatn=θΔat0+nΔθΔat

(60)

其中,θΔet0、θΔat0分别为俯仰角与方位角的起始搜索角度,ΔθΔet、ΔθΔat分别为俯仰角与方位角的搜索角度间隔。

对于任意给定的θΔet、θΔat,将式(54)所表示的优化模型转化为对矩阵S的无约束二次优化模型,由于目标函数tr[(X-AS)H(X-AS)]为矩阵S的凸函数,其最优解可以通过下面的方法求得,令:

ξ=tr[(X-AS)H(X-AS)]

(61)

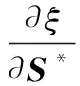
(62)

当∂ξ/∂S*=0时,可得矩阵S的解为

(63)

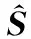
tr{[X-A(AHA)-1AHX]H[X-A(AHA)-1AHX]}

(64)

通过分析可知,式(64)为目标来向θΔet、θΔat的二维函数,因此通过对目标角度进行二维搜索,即可获得目标函数的最小值,即:

arg min tr{[X-A(AHA)-1AHX]H[X-A(AHA)-1AHX]}

(65)

在二维角度搜索过程中,θΔet、θΔat分别按照下列公式进行步进:

θΔet(m)=θΔet0+mΔθΔet

(66)

θΔat(n)=θΔat0+nΔθΔat

(67)

由式(64)可知,应用“残差矩阵F-范数最小化”准则可使接收信号X在目标、干扰增益矩阵A的正交补空间投影信号能量达到最小化,从而得到目标与干扰信号的最优估计。其中,干扰信号导向矢量由各通道信号估计得出,目标信号导向矢量通过式(65)所示的搜索算法得出。通过对比式(28)、式(29)与式(64)、式(65)的目标角度估计方法可知:MLC单脉冲算法只运用干扰对消后的两通道信号,目标角度直接通过差、和信号电压比值确定,受干扰信号残差影响较大;本文算法运用了全部通道信号,目标角度由“残差矩阵F-范数最小化”准则确定,受干扰信号残差影响较小。

2.4 算法流程

本文算法流程如下。

算法 主瓣掩护式干扰背景下目标角度估计算法输入 单脉冲雷达接收到的信号:X输出 目标俯仰角与方位角估计(1) 干扰信号来向估计:w^Δe=xΔejxHΣjxΣjxHΣjw^Δb=xΔajxHΣjxΣjxHΣjw^ΔΔ=xΔΔjxHΣjxΣjxHΣj(2) 目标角度估计:[S^,θ^Δet,θ^Δat]=arg minS,θΔet,θΔat|X-AS|2FS^=(AHA)-1AHX[θ^Δet,θ^Δat]=argmintr{[X-A(AHA)-1AHX]H·[X-A(AHA)-1AHX]}θΔet(m)=θΔet0+mΔθΔetθΔat(n)=θΔat0+nΔθΔat

3 复杂度分析

由于MLC单脉冲算法与本文算法在计算过程中主要用到了复数的乘法运算,对于加(减)法、除法等运算的使用次数较少,可忽略不计,故本文在分析复杂度时只对乘法的运算量进行计算,并在计算复杂度时设定目标回波点数为M。

3.1 MLC单脉冲算法复杂度分析

MLC单脉冲算法的运算量主要由系数ve、va的求解产生,由式(26)和式(27)可知,算法共进行了8次向量间Hadamard积的运算,其运算量为

T0=32M

(68)

则MLC单脉冲算法的复杂度为

T(M)～O(M)

(69)

3.2 本文算法复杂度分析

T1=24M

(70)

随后需要对矩阵A进行确定,通过干扰信号来向可确定矩阵A中干扰信号的归一化增益,由式(56)～式(58)可知,该过程与式(51)～式(53)一致,无需重复计算。为确定矩阵A中各通道的目标信号增益,需在搜索范围内进行m×n次搜索,每次搜索均需进行矩阵S估计和目标角度估计。

在进行矩阵S估计时,由于A为4×2阶矩阵,则(AHA)-1AH的复杂度与M无关,复杂度量级相对于M为常量阶,故其运算量可忽略不计。因此,由式(63)可知,矩阵S估计的运算量约为

T2=32M

(71)

求得矩阵S后可进行目标角度估计。同理,A(AHA)-1AH的运算量可忽略不计。由式(64)可知,目标角度估计的运算量约为

T3=128M

(72)

故由式(65)可进一步得出本文算法的总运算量为

T=T1+mn(T2+T3)=(160mn+24)M

(73)

因此,本文算法的复杂度为:

T′(M)～O(M)

(74)

由式(68)、式(69)与式(73)、式(74)可知,本文算法的运算量高于MLC单脉冲算法,但复杂度量级均为线性阶。目前的高速信号处理器具有强大的数据运算能力,完全可以满足本文算法的运算要求。

4 仿真验证

4.1 参数设置

本文实验仿真采用阵元个数为80×80的单脉冲雷达系统,阵元间距为半波长,方位维、俯仰维天线波束指向均为0°,搜索范围均为1°,搜索角度间隔均为0.02°。干扰信号来向为方位角-0.05°、俯仰角0.05°,目标信号来向采取俯仰角与方位角相等的方式,均在-0.5°至0.5°,每隔0.1°取1个角度值,共计11个角度值。随后,分别在俯仰角与方位角的每个角度值上进行5 000次蒙特卡罗实验仿真,最后取5 000次仿真结果的平均值作为算法对该角度值的测量结果。

4.2 实验结果

图2和图3为4组主瓣掩护式干扰条件下和差单脉冲算法、MLC单脉冲算法以及本文所提算法对目标俯仰角和方位角的测量结果,其中分图(a)、分图(b)、分图(c)、分图(d)的信干比(signal to interference ratio, SIR)分别为-20 dB、-30 dB、-40 dB、-50 dB。

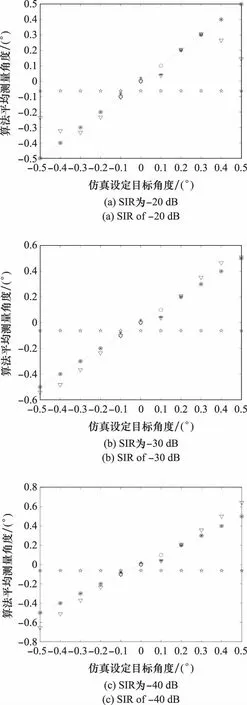
图2 目标俯仰角度测量结果Fig.2 The measurement result of target pitch angle

图3 目标方位角度测量结果Fig.3 The measurement results of target azimuth angle

从图2和图3可以看出,和差单脉冲算法测量出的目标角度与仿真设定干扰角度基本一致,无法反映目标位置,说明主瓣掩护式干扰背景下和差单脉冲算法无法测量目标角度。MLC单脉冲算法在目标与干扰的夹角小于0.2°时能够较为准确地测量出目标角度,但随着目标与干扰的夹角逐渐增大,算法的测量准确度逐渐降低,并且SIR对该算法的测量准确度影响较大。当SIR为-30 dB时,MLC单脉冲算法的测量结果较为准确;当SIR过小或者过大时,MLC单脉冲算法的测量准确度均会有所下降。本文算法能够在所有仿真设定目标角度上取得较好的测量结果,但在干扰附近时,算法的准确度有所降低。此外,算法的测量准确度基本不受SIR的影响。

图4和图5为MLC单脉冲算法与本文算法的测量误差在拉依达准则(3倍标准差准则)下的统计结果。

图4 目标俯仰角度测量误差拉依达准则统计结果Fig.4 Statistical results of measurement error of target pitch angle based on Pauta criterion

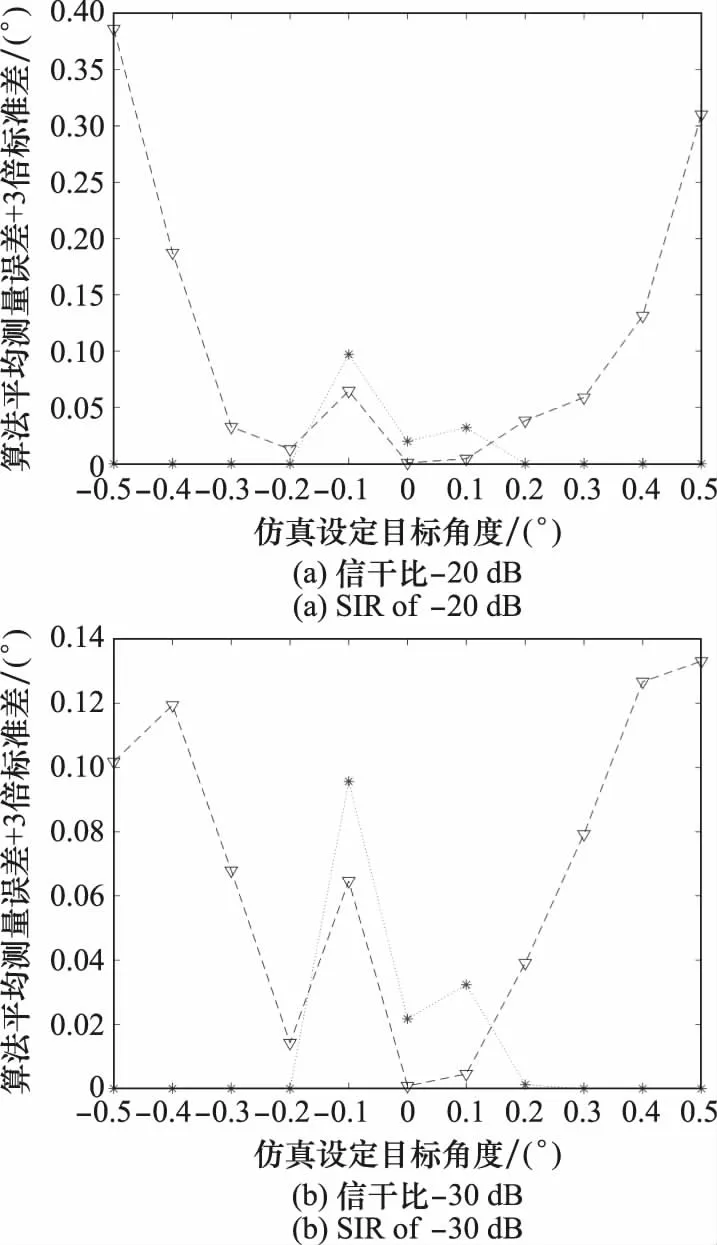
图5 目标方位角度测量误差拉依达准则统计结果Fig.5 Statistical results of measurement error of target azimuth angle based on Pauta criterion

由拉依达准则可知,算法的测量误差小于算法平均测量误差+3倍标准差的概率为99.7%。从图4和图5可以看出,当目标与干扰的夹角大于0.2°时,MLC单脉冲算法的测量误差较大且分布区间较广,算法性能较差;本文算法的测量误差较小且测量误差分布较为集中,算法性能较好。当目标与干扰的夹角小于0.2°时,本文算法与MLC单脉冲算法的性能相差不大。

5 结 论

本文提出了一种主瓣掩护式干扰背景下单脉冲雷达的角度估计算法。该算法首先通过雷达接收信号估计出干扰信号的来向,随后从接收信号中提取出干扰与目标回波信号,最后通过优化模型估计出目标角度。由于本文算法运用了全部通道信号,目标角度由“残差矩阵F-范数最小化”准则确定。在算法性能上,本文算法比传统的MLC单脉冲算法测角精度更高,稳定性更强,虽在运算量上有所增加,但当前雷达信号处理系统主要采用“DSP+FPGA”处理平台,完全能够满足本文算法的运算要求。后续将对算法进行改进,进一步提升目标方向与干扰方向夹角较小时的算法性能。