定常振荡流施肥模式对灌溉管道混合均匀性的影响

李 杰，李俊龙，张以升

（郑州大学 水利与土木工程学院，郑州 450001）

0 引 言

【研究意义】水肥一体化技术是一种新兴的农业灌溉新技术，水溶性肥液通过注肥设备进入灌溉管道后，与主干管中的水充分混合后进入支管，再经由毛管分配给各灌水器进而实施灌溉，水肥一体化能够最大程度地节约水肥资源提高施肥效率[1-3]。肥液与水的混合均匀性是决定水肥利用效率的重要因素，一般来说，肥液与水在进入第一级支管前充分混合，可大大提高水肥利用效率，因此研究定常振荡注肥模式对灌溉管网首部主干管道水肥混合均匀性的影响十分重要。【研究进展】Vicent 等[4]研究发现，管道入口角度趋近于90°时数值仿真结果与室内管道试验结果之间的误差小于10%；Walker 等[5]研究发现，在使用k-ε湍流模型时增加模型系数可改善肥液浓度与速度分布的一致性；Yenjaichon 等[6]研究发现，当注入模式由近壁注入改为射流混合时肥液混合质量会得到显著的提高；Lin 等[7]研究表明，在T 型管热混合过程中二次流对混合过程起重要作用；Akbari 等[8]研究将重流体注入轻流体的过程发现，随着重流流速的增加，流体之间的混合更加充分；殷鹏飞等[9]研究发现，在一定范围内提高水肥流速，降低其流速比及管径比，可有效提高水肥的混合效果，促进水肥混合均匀性；朱金铤等[10]研究发现，流量比对注肥三通管直通局部阻力系数有显著影响，管径比对局部阻力系数无显著影响；Sun 等[11]通过建立数值模型，探究了恒定流情况下管道盐溶液与水的混合过程，并通过管道试验验证了数值仿真结果的可靠性，但未探讨定常振荡流情况下液体混合过程；Zhang 等[12]对定常振荡注肥模式下，灌溉管道内水肥混合规律进行了试验研究，考察了部分管道结构参数、水力参数和肥料物理性质对水肥混合均匀性的影响，但未考虑温度对水肥混合过程的影响。【切入点】在实际喷滴灌工程中，多采用柱塞泵[13]以脉冲注肥方式向灌溉管道中注入肥液，实际为定常振荡流在管道中的液-液混合，目前关于此过程的研究较少，特别是针对影响水肥混合过程的重要影响因素的研究以及混合机理的分析不够具体。【拟解决的关键问题】本研究拟采用管道试验与数值仿真的方法探究定常振荡流时不同灌溉主管管径、温度、主管流量以及注肥比的情况下管道中水肥混合规律，提出定常振荡流情况下施肥管道支管的安全开口位置，对达成灌溉与施肥过程有机结合、节约水肥资源以及提高施肥效率有重要意义。

1 材料与方法

1.1 试验设计

为验证数值仿真结果的准确性设计了物理试验，试验在室内常温下进行。试验系统分为3 个部分：灌溉水控制系统、注肥系统以及水肥混合管。灌溉水控制系统以10 m3水箱作为水源，通过变频控制柜（宝鸡市秦川测控科技有限公司）控制水泵以及电磁流量计（CKLDG/LDG，中国，精度为±0.5%）对灌溉管道主管流量进行控制，基于工程实际选择了灌溉主管管径（D=63、90、110 mm），灌溉主管采用PVC 材料。注肥系统中柱塞泵进出肥管道均采用聚乙烯（PE）管道，直径为d=12 mm，注入混合管道之中的肥液是固体肥液与水混合稀释后的溶液，试验采用固体肥料为复合肥（ω（N+P2O+K2O）≥40%），注肥量采用动态称质量法进行测定，即根据1 min 内抽取的肥液质量换算得到平均注肥流量，试验使用的储肥桶容积为30 L，电子秤（正峰T1 台秤）量程为75 kg，精度为1 g。为确定水肥混合管道中水肥的混合情况，沿管道中心线布置了上下共34 根取样管，取样管采用直径8 mm、长度50 mm的聚乙烯管道，间隔为0.5 m。

试验考虑了灌溉主管管径（D）、温度（T）、主管流量（Q）以及注肥比（δ=q/Q）对水肥混合均匀性的影响。试验通过变频控制柜和电磁流量计控制主管流量，待管道流量稳定后，通过柱塞泵向管道中注入肥液。为确保肥液与灌溉水充分混合，在开始注肥5 min 后取样。以第1 根取样管道为P1，每隔1 min 对下1 根取样管进行取样，每根取样管进行3 次取样，使用电导率仪（DDSJ-319L）测定P1—P17 共计34 个样品电导率并转换成肥液质量分数，试验影响因素具体如表1 所示。

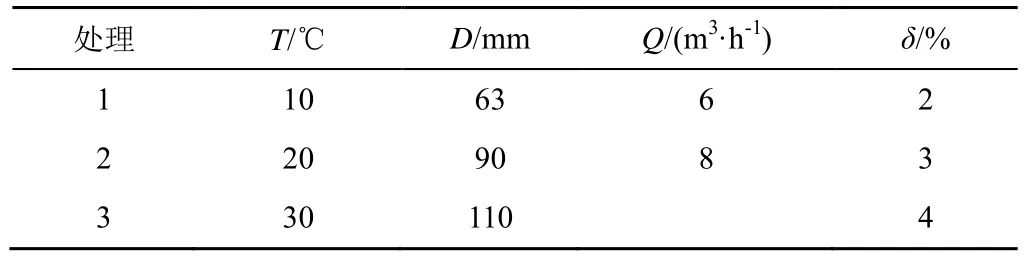
表1 试验因素水平Table 1 Experimental factor levels

1.2 数值仿真

1.2.1 模型建立

采用有限元分析软件 Ansys（2021R1）中的CFD 模块建立了如图1 所示的T 形三通管几何模型。模拟管道模型的长度为10 m，直径为12 mm 的垂直射流注肥口中心处与横向灌溉注水口的距离为1.5 m。根据所建立的几何模型，采用六面体结构网格进行绘制，不同管径（D=63、90、110 mm）主管的网格数分别为545 374、756 862、897 654 个，图1 所示注水口的直径D=63 mm。

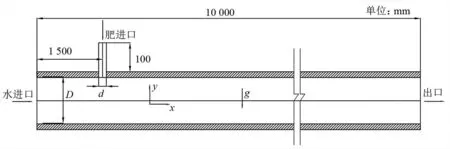
图1 混合管道数值模型Fig.1 Numerical model of mixed pipe

1.2.2 控制方程

在混合过程中竖直注肥管与横向灌溉管道中的液体流动状态均为湍流，湍流模型使用了应用范围广、精度更高的重新整化群（RNG）k-ε模型[13-14]，肥液与水的混合本质上为不同溶质液体的混合，混合模型采用组分运移模型（Species Transport）。

连续性方程：

式中：k为流体相数；ρ为流体密度（kg/m3）；φ为流体体积分数；ν̅为流体平均速度（m/s）。

动量方程：

式中：p为压力（Pa）；τ为分子动量（N/m2）；g为重力加速度（m/s2）；F为体积力（N/m3）。

第k相的体积分数方程：

式中：νdr,k为第k相的滑移速度（m/s）；νk为混合相的流速（m/s）。

1.2.3 边界条件

在肥液与水的混合模拟中，水进口与肥进口均采用速度入口，数值模型中填充的流体材料分别为水和肥料的溶液，流体材料的密度与黏度会对混合效率产生影响，使用的流体材料属性如表2。

表2 流体材料属性Table 2 Properties of fluid material

肥液通过柱塞泵脉冲注入混合管道中，肥液流量变化曲线计算式为：

式中：qf为肥液注入时的瞬时速度（m/s）。

注肥口与注水口的速度由流量决定，速度计算式为：

式中：D为灌溉主管直径（mm）；d为注肥口直径（mm）。壁面采用无滑移条件，近壁区采用标准壁面函数[15-16]。出口选择压力出口，动量、体积分数和湍动能采用一阶迎风式离散，计算时间步长确定为0.01，迭代次数为1 500 次，计算总时间为15 s。

1.2.4 网格无关性检验

以T1D1Q1δ1 为例，选择了3 种不同的尺寸对数值模型进行网格划分，网格总数分别为545 374、600 345、642 321 个。在相同的边界条件下，对3 种不同网格划分的数值模型，比较相同位置肥液质量分数。如表3 所示，在不同的网格数目下，相同位置的肥液质量分数基本无变化，故选择网格数目为545 374 的划分尺寸，以达到减少模拟时间的目的。

表3 T1D1Q1δ1 工况下网格的无关性检验Table 3 Mesh independence study for T1D1Q1δ1 conditions

1.3 数据处理

肥液与水在混合管道的混合本质上为两相流混合，为判断管道中水肥混合情况，本研究拟采用偏差系数法作为混合均匀评价指标，在管道截面上距离管壁2 mm 处从原点处顺时针依次取9 个点，计算截面的偏差系数。偏差系数越小则表示混合越均匀，φ≤0.01 时视作混合均匀[17]。理想状态下肥液从开始注入混合均匀的过程中，偏差系数值逐步变小最后趋于0。本研究测量了不同位置的采样管中混合液体的电导率，进而可以判断水肥混合管道系统中水肥混合均匀的位置。

1.4 模拟可靠性验证

通过电导率与肥液质量分数的关系，将试验实测混合溶液浓度转化为肥液质量分数与数值模拟结果进行比较，图2 展示了主管流量Q=6 m3/h 时，不同注肥比（2%、3%、4%）工况下肥液质量分数随混合距离的变化。由图2 可知，实测肥液质量分数与数值模拟计算结果吻合较好，在3 种工况下，上部取样管的肥液质量分数沿混合距离逐渐变小，下部取样管的肥液质量分数则随混合距离的增加逐渐变大，模拟结果中肥液沿程质量分数变化趋势与3 种工况下的试验结果趋于一致，采样管上部的相对误差为9.82%，采样管下部相对误差为5.01%，均小于10%。

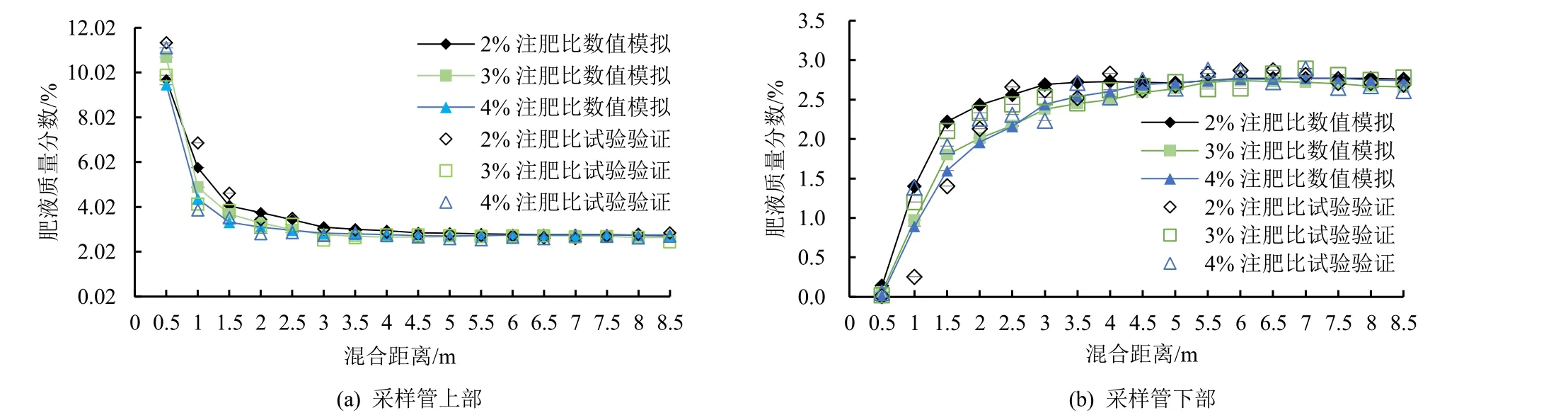
图2 试验结果与模拟结果对比Fig.2 Comparison of experimental and simulated results

2 结果与分析

2.1 混合过程与肥液质量分数变化

图3 为T1D1Q1δ1 工况下肥液混合云图。在肥液注入前，管道中被水充满；肥液注入管道后，肥液逐渐被稀释，但肥液与水之间存在明显的分层现象。随着混合过程的进行，肥液与水的混合均匀性进一步提升，肥液质量分数随混合距离的增加逐步减小，混合区域沿重力方向与管道x轴方向逐步扩大，沿x轴各肥液质量分数分层之间的间隔逐渐缩小。

图3 肥液质量分数轴向分布Fig.3 Mass fraction of fertilizer along the path

如图4 所示，根据采样管的布置沿x轴每隔0.5 m 取管道yz面截面，P0 处为注肥口截面。肥液注入混合管道后同时沿重力方向与灌溉水流方向扩散，受壁面的影响肥液的横向扩散速度远小于纵向扩散速度，随着混合距离增加，肥液与水混合而充满管道上部，肥液沿壁面的扩散速度超过纵向的混合速度，如图中P2 位置所示，肥液与水的混合速度加快最终在P4 位置（距注肥口大约3.8 m 处）开始混合均匀。

图4 沿x 轴肥液质量分数径向分布Fig.4 Mass fraction of fertilizer along the radial direction at different axis positions

沿程偏差系数变化如图5 所示。随着混合距离的增大偏差系数逐步减小，水肥混合均匀性逐步提高，最终在3.5～4 m 处混合均匀。

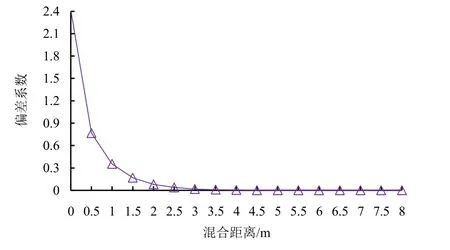
图5 偏差系数沿程变化Fig.5 Variation of deviation coefficient along the path

2.2 有效混合距离

偏差系数趋近于0.01 时，管道截面之间肥液质量分数变化可忽略不计。因此，当偏差系数[18]趋近0.01 时可认为水肥混合过程完成，故拟定以偏差系数φ=0.01 时的混合距离为有效混合距离，分析不同因素水平对有效混合距离的影响，各工况下的有效混合距离如表4。

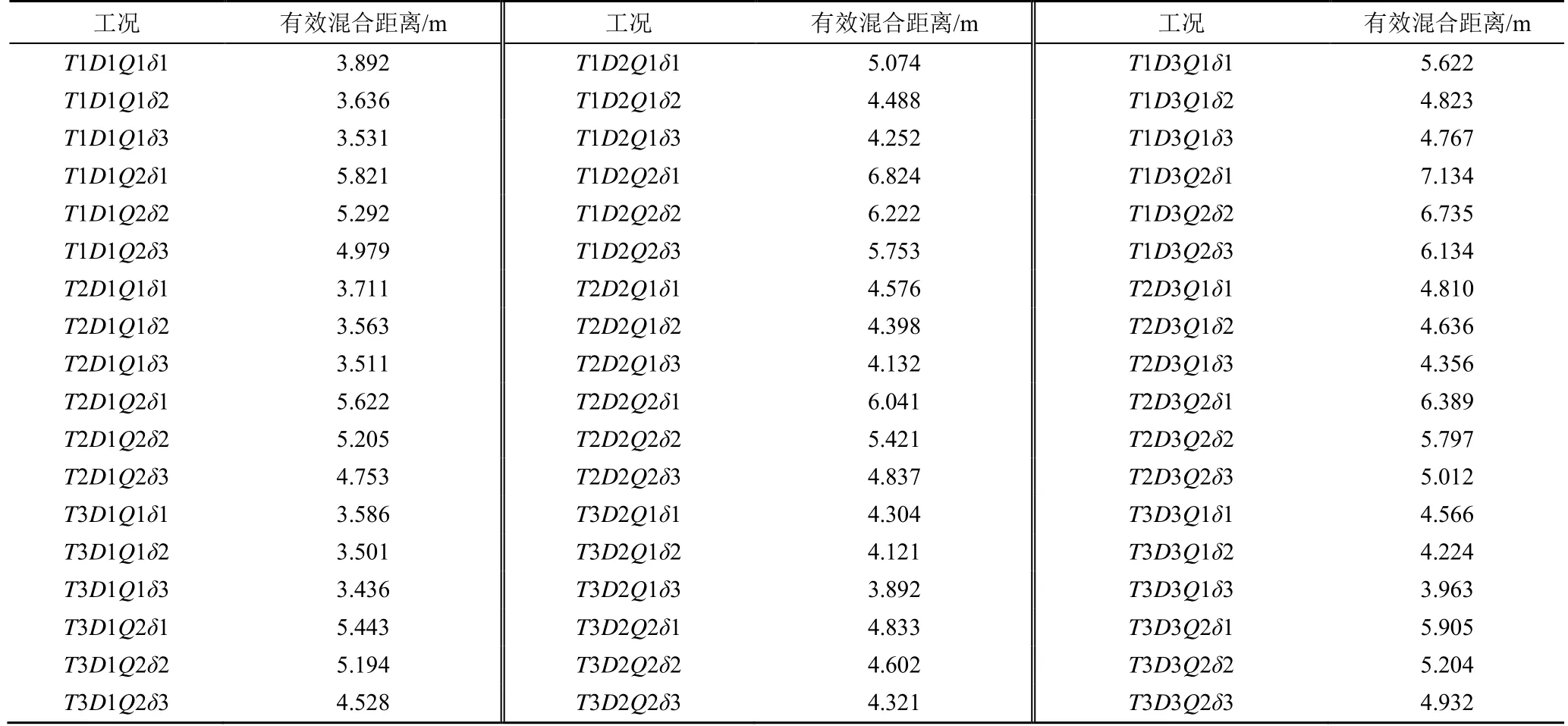
表4 不同工况下的有效混合距离Table 4 Effectivemixing length under different working conditions

相同温度下（T=20 ℃），管径与流量及注肥比对有效混合距离的影响如图6 所示。在流量与注肥比相同的工况下，管径从63 mm 增大到110 mm 时，有效混合距离平均增加了约0.769 m；注肥比相同，主管流量（Q）从6 m3/h 增加到8 m3/h 时，不同管径下的有效混合距离平均增加了 1.598、1.064、1.132 m。显然，较大的管径与主管流量会对管道中水肥混合带来不利的影响，随着二者数值的增加所需的混合距离会逐步增大，并且根据有效混合距离的变化幅度可知，主管流量对有效混合距离的影响较为显著。

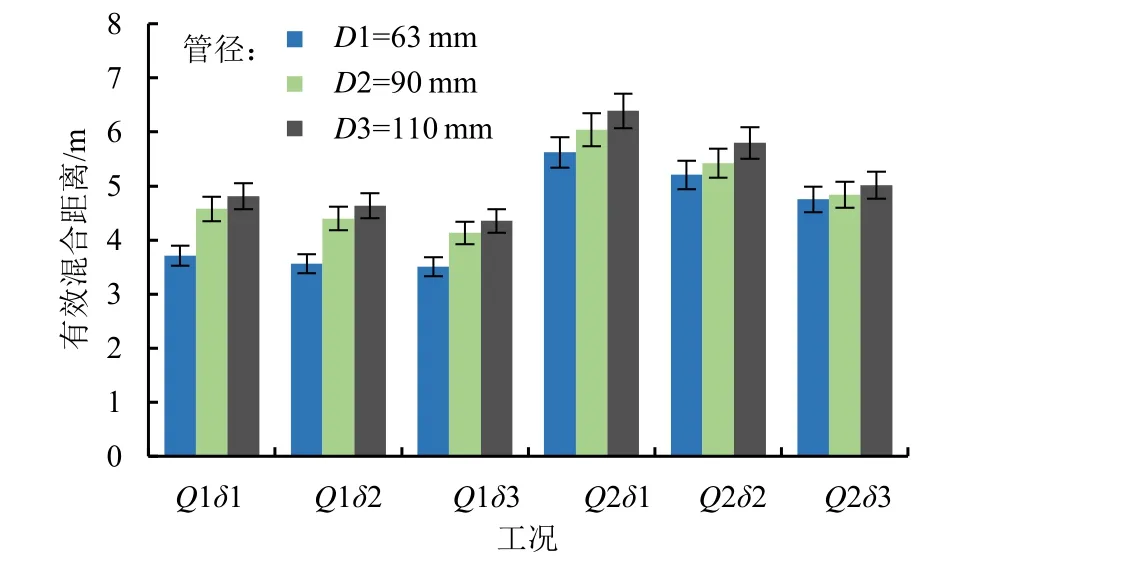
图6 不同管径下有效混合距离随主管流量和注肥比的变化Fig.6 Effective mixing distance as a function of the main flow and injection ratio under different pipe diameter

主管流量相同，注肥比（δ）从2%增加到4%时，不同管径下的混合距离平均减少了0.758 m，注肥比与有效混合距离负相关，但不同主管流量下注肥比的增加对有效混合距离的影响存在明显差异，如图7 所示。在Q=6 m3/h 时，随着注肥比的增加，有效混合距离平均减少了0.366 m；而当Q=8 m3/h 时，有效混合距离平均减少了1.15 m。由有效混合距离的变化幅度可以得到，当主管流量较大时，增大注肥比可有效缩短有效混合距离。

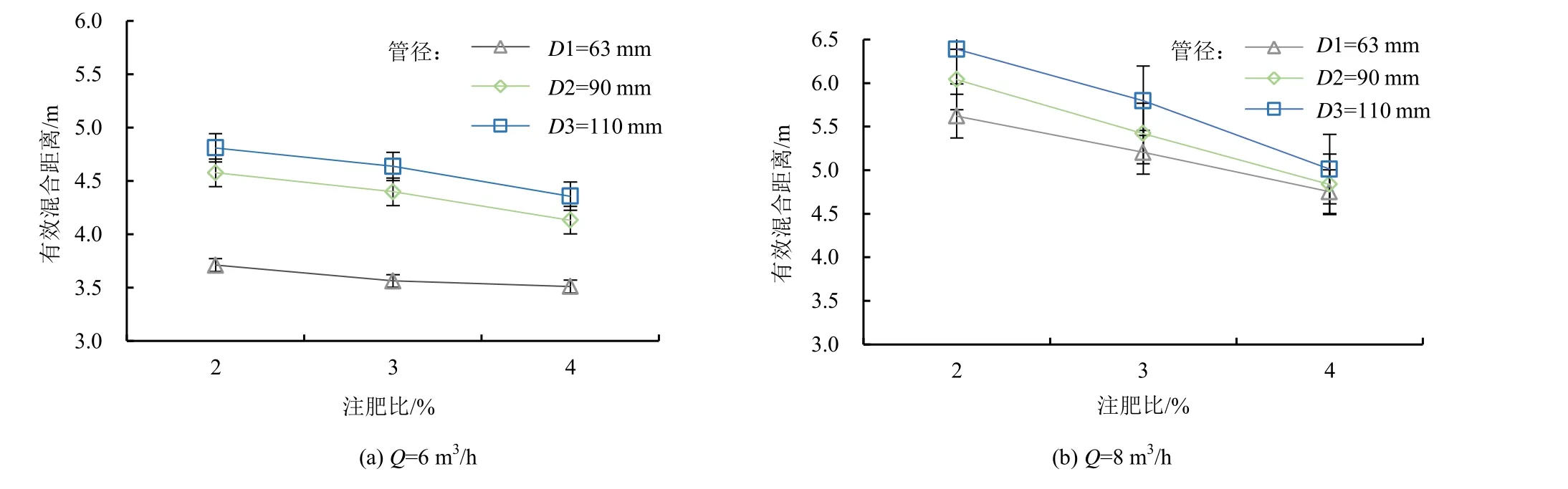
图7 不同注肥比下有效混合距离的变化趋势Fig.7 Variation trend of effective mixing distance under different fertilizer injection ratio

选取管径（D=90 mm）为定值，探究温度对有效混合距离的影响。图8 显示了在不同肥液温度梯度下各工况的有效混合距离变化趋势，随着温度的增加有效混合距离总体呈下降趋势。在Q=6 m3/h 时，温度从10 ℃升高至30 ℃，有效混合距离平均下降了0.499 m；而在Q=8 m3/h 时，有效混合距离平均下降了1.681 m。故当主管流量较大时，温度对有效混合距离的影响较为显著。

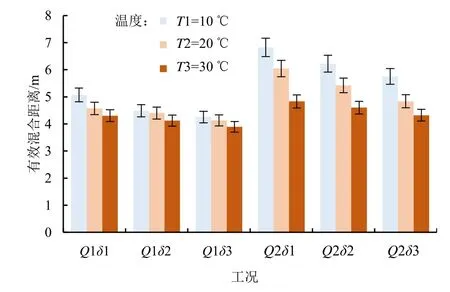
图8 不同温度下有效混合距离随主管流量和注肥比的变化Fig.8 Effective mixing distance as a function of the main flow and injection ratio under different temperature

由表5 可知，主管管径、温度、主管流量和注肥比均显著影响有效混合距离，与管径、温度和注肥比相比，主管流量对有效混合距离的影响效果最为明显，主管管径对有效混合距离的影响次之。

表5 各因素对有效混合距离的方差分析Table 5 Analysis of variance between each factor and effective mixing length

2.3 混合机理分析

肥液在刚注入管道时偏差系数急剧减小，随着混合距离的增大，偏差系数的变化幅度逐步减小最终趋于稳定，在这期间管道中流体的流态发生了剧烈变化。图9 为T3D1Q1δ1 工况下管道横截面的流速。由图9 可知，肥液注入管道后，在注肥管道与主管管道交界处的上部立即出现了2 个涡并且向四周扩散，管道中央的流速变化十分剧烈。随着混合距离的增大，沿中轴线右边的涡逐步扩大而左边的涡逐步缩小最终合并，管道内流场趋于稳定，此时管道中肥水混合基本完成。

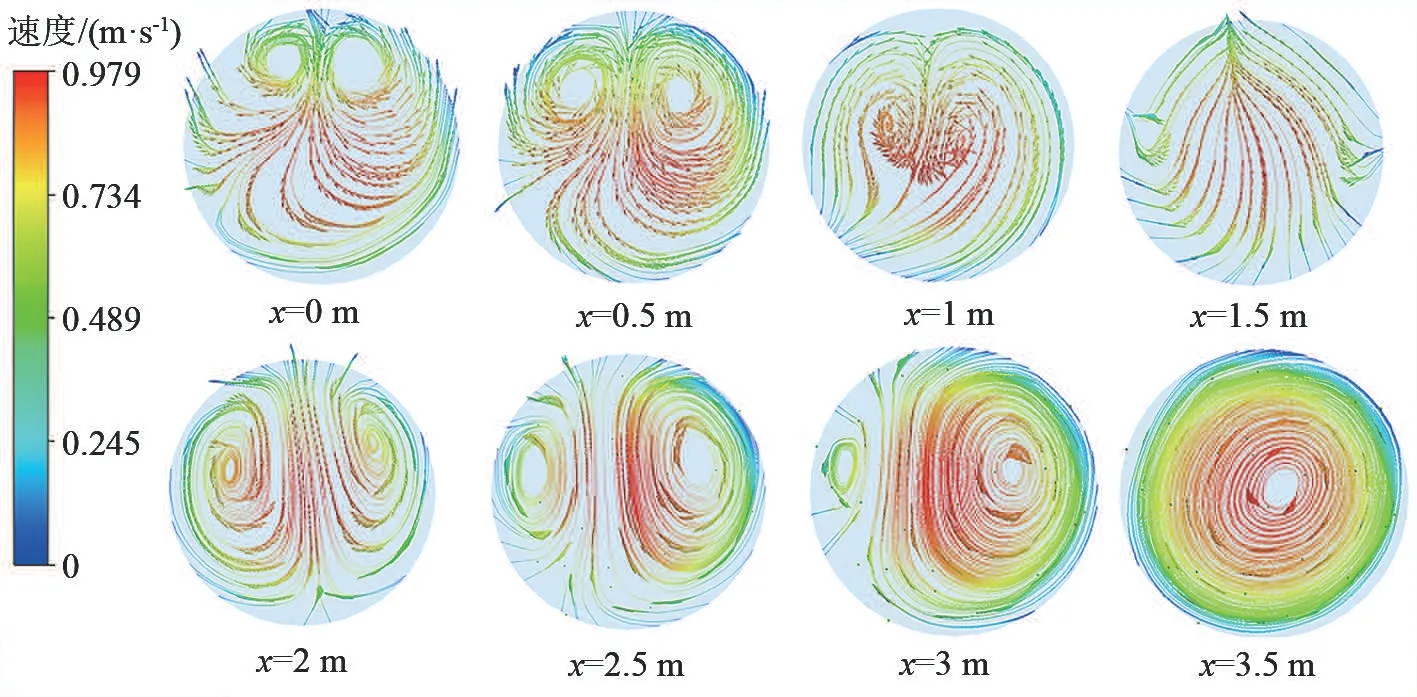
图9 沿x 轴肥液流速的变化Fig.9 Changes of velocity along the x axis

2.4分干管安全开口位置

在灌溉系统中水肥混合均匀所需要的混合距离，对于节约水肥资源，提高水肥利用效率以及施肥策略的发展具有重要意义，在工程实际中，水肥混合均匀进程通常在20 ℃左右，根据数值仿真结果，主管流量Q=6 m3/h 时不同管径的平均有效混合距离分别为3.595、4.369、4.601 m；主管流量Q=8 m3/h 时不同管径的平均有效混合距离分别为5.193、5.433、5.733 m。综合模拟结果，在定常振荡流情况下分干管的开口位置应位于距注肥口5～5.5 m 处，在温度较低的情况下，应适当地降低主管流量以及使用管径更小的灌溉主管，而在主管流量较大的情况下可通过提升注肥比减少有效混合距离。

3 讨 论

数值模拟可用于探究定常振荡流注肥模式下管道中的水肥混合问题。肥液注入灌溉管道后，在灌溉管道相同位置处，数值模拟结果与室内管道试验测量值吻合较好，肥液质量分数的相对误差小于10%，表明通过CFD 建立数值模型解决灌溉管道中水肥混合问题是可行的，这与Sun 等[11]的研究结果相似。本研究采用定常振荡流注肥模式与大多数针对水肥混合过程的研究[9-10]所使用的恒定流注肥模式存在一定的差异性，这主要是因为实际的喷灌工程中肥液多采用柱塞泵[13]脉冲注入管道，定常振荡流注肥模式更贴近于现实情况。

本研究中，水肥混合均匀所需的有效混合距离随管径与主管流量的增加而增加，这与Zhang 等[12]研究结果一致。这是因为在管径恒定的情况下，主管流量的增加，会引起灌溉水流速的增加，肥液脉冲注入时与其接触的部分相对减少，肥液浮于管道顶部的情况加剧，向外扩散的速度减慢。与此同时，灌溉水流速的增加伴随着更强的速度剪切，会带来巨大的能量损失，从而导致水肥混合的进程减慢，表现为所需的有效混合距离更长。较大的管径增加了肥液的扩散面积，在主管流量与注肥比恒定的情况下，管径越小越有利于肥液的扩散，有效混合距离越短。在较大的主管流量下，注肥比的增加可有效减少有效混合距离，在Q=6 m3/h 时，随着注肥比的增加，有效混合距离平均减少了0.366 m；而当Q=8 m3/h 时，有效混合距离平均减少了1.15 m。注肥比的增加带来了更大的注肥量，在注肥管管径恒定的情况下，注肥量的增加会带来更大注肥速度，使水肥混合更加充分，表现为所需的有效混合距离减少，这与Akbari 等[8]的研究结果相似。此外，温度作为灌溉工程中不可忽略的环境因子，对于加快水肥混合进程有重要影响，这一作用在主管流量较大时更为显著，在Q=6 m3/h 时，温度从10 ℃升高至30 ℃，有效混合距离平均下降了0.499 m；而在Q=8 m3/h 时，有效混合距离平均下降了1.681 m，这是因为温度的增加会使流体的粘滞性降低，流动性增加，加快了水肥混合的进程，表现为所需的有效混合距离变短。此外，注肥时肥液与灌溉水的接触会形成涡流，涡流的产生与消解带来的是肥液与水的充分混合，而温度的增加会加剧此过程。

4 结 论

1）管道试验中肥液质量分数分布与数值模拟结果基本吻合，水肥混合变化趋势一致。

2）水肥混合程度随着混合距离的增加而提升，此过程伴随着涡的产生与消解。

3）水肥混合均匀所需的有效混合距离随管径与主管流量的增加而增加，随温度与注肥比的增加而减少，主管流量的影响最为显著，管径次之；采用直径为63、90、110 mm 灌溉主管，分干管的开口位置应距注肥管道5～5.5 m 处。

（作者声明本文无实际或潜在的利益冲突）