肥液浓度对双点源涌泉根灌土壤入渗特征及水分运移的影响

张俊，缑丽娜，何振嘉，肖欣怡，梁飞，任虎兴，傅渝亮

（1.陕西省土地工程建设集团有限责任公司，西安 710075；2.华北水利水电大学水利学院，郑州 450045）

0 引 言

干旱缺水是限制我国节水农业发展的重要影响因素之一，我国农业灌溉保证率较低，尤其是地面灌溉等方式造成的水资源浪费较大，不利于我国节水灌溉的进一步发展，地下灌溉方式因能够有效减少水分损耗而受到国内外学者的普遍关注[1-3]。涌泉根灌是吴普特等[4]在陕北山地枣树种植中推广应用的一种微灌技术，是在滴灌基础上优化发展而来的地下局部灌溉。该灌水技术可将水肥直接输送至果树根区，可极大避免传统地面滴灌中地表水肥损失，有效提高水肥利用效率[5,6]。此外，涌泉根灌灌水器套管的保护避免了滴头与土壤直接接触，降低了滴头堵塞率，且其制作材料价格低廉，与传统滴灌相比具有较高的性价比优势，对于果树节水灌溉具有较大的应用推广价值[7]。

国内学者对涌泉根灌单点源入渗条件下土壤水分运移特性已有较多研究。费良军等[8,9]研究了不同流量和土壤容重条件下涌泉根灌土壤水分入渗特性和运移规律。樊晓康等[10]研究了不同灌水量和灌水器埋深条件下涌泉根灌土壤水分入渗规律。牛文全等[11]和刘显等[12]研究了土壤初始含水率对涌泉根灌湿润体特性的影响,丰富了涌泉根灌技术要素。水和肥是保障作物生长必备的2项重要影响因子，随着水肥一体化技术的广泛研究与应用，肥液入渗也是研究涌泉根灌灌水器相关技术参数的重点方向。费良军等[13]、何振嘉等[14-16]、刘显等[17,18]以涌泉根灌土壤水分入渗和运移相关研究为基础，对涌泉根灌水肥运移和氮素分布情况进行了大量试验，取得了一定成果，但多数研究主要基于单点源入渗。在生产实践中，双点源（或多点源）布置形式更为常见，且双点源（或多点源）交汇入渗较单点源入渗过程也更为复杂。目前，水肥共施条件对涌泉根灌双点源交汇入渗水氮运移特性影响的研究较少[19-21]。刘显等[22]对涌泉根灌双点源交汇入渗水氮运移特性进行了初步探讨，但其研究重点主要集中于不同灌水器间距条件对水氮运移和分布的影响。本文在肥液入渗基础上，研究不同肥液浓度对涌泉根灌交汇入渗湿润体相关技术参数及水分运移的影响，探究了双点源入渗与单点源的差异，为涌泉根灌技术的科学应用和灌水器相关技术参数的优化提供必要参考。

1 材料与方法

1.1 试验地概况

试验在陕西榆林市米脂县西北农林科技大学远志山试验基地(37°40′-38°06′N，100°15′-110°16′E)开展，属典型的黄土高原丘陵沟壑区域，气候为半干旱地区，年均降水量为451.6 mm。供试土壤为黄绵土，试验土壤颗粒组成使用英国马尔文仪器公司生产的Mastersizer-3000激光粒度分析仪测定，土壤中黏粒（＜0.002 mm）、粉粒（0.002～0.05 mm）、砂粒（0.05～2 mm）所占百分比分别为17.55%、42.59%、39.86%，根据卡庆斯基制分析土壤质地为壤土；土壤平均干容重为1.31 g/cm3，初始含水率为10.4%，田间持水率为23.4%，饱和含水率为39.8%；土壤较为贫瘠，有效N、P和K质量分数分别为34.74、2.91和101.9 mg/kg，有机质含量占比为0.21%，土壤平均NH4+-N含量为0.89 mg/kg，平均NO3--N含量为12.63 mg/kg；土壤pH为8.6，偏碱性。

1.2 试验装置及设计

试验装置由马氏瓶、灌水器和土壤剖面组成。马氏瓶截面积70.88 cm2，提供恒定水头并通过旋钮调节灌水器流量。灌水器通过橡胶管与马氏瓶连接，灌水器由灌水器内芯、过水流道以及配套套管组成，灌水器内芯套管中布设过水流道，高30 cm，外径4 cm，灌水器与配套套筒管通过螺口直接安装或拆卸，配套套管为PVC材料，壁厚2 mm，内径4 cm，出水口位于内芯内侧，水分在流道中经过消能从出水口流出，再经由套管以面源出流的方式导入土壤进行灌溉。灌水器上方有连通气孔，通过调节马氏瓶底部旋钮控制灌水时间和灌水流量，结合试验区土壤导水特性，模拟灌水器流量为5 L/h，使用秒表和20 mL量筒率定滴头流量，并校验试验过程中部分时刻的灌水器流量，确保供水稳定。试验灌水器间距50 cm，灌水器埋深15 cm，套管开孔率20%；肥液质量浓度设置5、10和20 g/L共3个梯度，以清水入渗作对照（CK），供试氮肥为尿素，为降低降雨和蒸发对湿润体的影响，试验结束后用塑料布遮盖湿润体，每组处理3次重复，取其均值作为试验结果。涌泉根灌示意图及试验系统示意图见图1、图2。

图1 涌泉根灌示意图Fig.1 Sketch map of bubbled-root irrigation

图2 试验系统示意图Fig.2 Experimental system structure

1.3 试验方法及观测内容

湿润锋观测采用剖面法，在试验区选择未经扰动的天然坡地，清除土壤表层覆土及杂草后，将剖面修整为光滑整齐的阶地，将水平和垂直剖面作为观测面，按照先密后疏的原则记录马氏瓶读数和湿润锋运移距离，不同时刻湿润锋运移距离使用钢卷尺直接在试验剖面上量出。交汇入渗发生后，以灌水器底部为起点，用直尺测量交汇面处湿润锋在竖直向上和竖直向下的运移距离，供水停止后，在距离灌水器0、12.5和25 cm（交汇面）处选用直径为5 cm的土钻分层取土，取土间隔为10 cm，用烘干法测定土壤含水率。

累积入渗量计算公式：

式中：I为累积入渗量，mm；r为马氏瓶底面半径，cm；h(t)为马氏瓶供水下降高度，mm，r′为灌水器套管半径，mm；h′(t)为不同入渗时间t内灌水器套管内积水深度，mm。

累积入渗量曲线利用Philip模型和Kostiakov模型对涌泉根灌双点源交汇入渗数据进行拟合。

Philip模型为：

式中：I为累积入渗量，mm；S为土壤吸渗率，mm/min0.5；t为入渗时间，min。

Kostiakov模型为：

式中：I为累积入渗量，mm；K为经验系数，mm/minβ；β为经验指数；t为入渗时间，min。

肥液浓度对涌泉根灌双点源交汇入渗条件下不同肥液浓度对土壤水分入渗特征的影响，利用增渗率Z（同一入渗时刻，肥液的累积入渗量较清水的增加量与清水累积入渗量的百分比）进行具体分析：

式中：Z为增渗率；IA为涌泉根灌双点源交汇入渗条件下清水入渗的累积入渗量，mm；IB为涌泉根灌双点源交汇入渗条件下肥液入渗的累积入渗量，mm。

1.4 数据分析

采用Microsoft Excel 2010分析软件处理试验数据并进行绘图，对相关试验数据进行Pearson相关检验和单因素方差分析，显著水平设定为P＜0.05。

2 结果与分析

2.1 肥液浓度对双点源涌泉根灌累积入渗量的影响

图3为肥液浓度分别为0、5、10和20 g/L单向交汇入渗整个过程累积入渗量变化曲线。可以看出，肥液促进了双点源涌泉根灌的土壤水分入渗。入渗70 min以内，不同肥液浓度累积入渗量差异不大，70 min后不同肥液浓度的累积入渗量差异逐渐增大。累积入渗量随着肥液浓度的增加而增加（P＜0.05）。这主要由于肥液入渗过程中，当毛管孔隙持水能力达到最大时，非毛管孔隙的大小决定土壤通气透水能力。土壤接近饱和状态时，由于尿素溶液中带负电荷的土壤胶体被肥液中带正电荷的铵根离子和钙离子所中和，肥液中的钙离子把土壤胶体中的钠离子进行置换，各个胶体之间产生吸引，有效改善了土壤团聚体的分布，特别是非毛管孔隙中的水稳性团聚体，孔隙中形成较好的通气透水能力，因此入渗率提高，导致相应时间段内的累积入渗量增加，肥液浓度越大，肥液中的正电荷越多，进而与带负电荷的土壤胶体中和幅度越大，相应产生的土壤团聚体越大，对肥液入渗的促进效果越显著[23]。

图3 不同肥液浓度条件下累积入渗量曲线Fig.3 Cumulative infiltration curve under the conditions of different fertilizer concentration

此外，随着肥液浓度的增大，湿润锋交汇的时间越短。这主要因为在水平方向湿润锋运移距离的差异主要受溶质势控制，肥液浓度越大，溶质势越小，湿润锋运移的势能差越大，湿润锋运移速度越快，交汇时间则越短。

对入渗70、150和300 min时不同肥液的累积入渗量分别与清水入渗（CK）进行比较（见表1），增渗率随着肥液浓度的升高显著增加（P＜0.05），随入渗时间延长显著增加（P＜0.05）。

表1 不同肥液浓度条件下增渗率比较Tab.1 Comparison of infiltration rate under different fertilizer concentration of fertilizer solution

2.2 肥液浓度对双点源涌泉根灌入渗模型参数的影响

依据实测数据（见图3），利用Philip模型和Kostiakov模型进行拟合，得到不同肥液浓度条件下涌泉根灌交汇入渗累积入渗量的数学模型（见表2）。2种入渗模型拟合效果较好，决定系数R2均能达到0.96以上。随肥液浓度增加，Philip公式吸渗率S逐渐增大，说明施加肥液可增强毛管力对土壤水分的吸收能力。原因是肥液中正电荷与带负电荷的土壤胶体中和形成水稳性团聚体，而水稳性团聚体是良好的土壤结构体，具有多孔性和水稳性特点；肥液浓度越大，肥液中的正电荷越多，形成的水稳性团聚体越多，土壤吸渗率也就越大。随着肥液浓度的增大，Kostiakov公式入渗系数K逐渐减小，经验入渗指数β逐渐减小，这表明肥液浓度的增加使土壤的初始入渗速率有所增加，提高了土壤入渗能力。

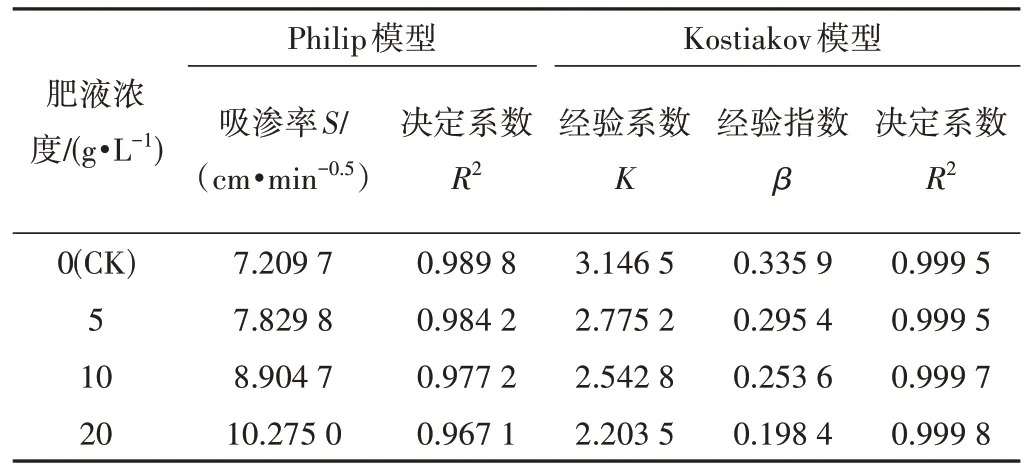
表2 累积入渗量拟合参数Tab.2 Fitting parameter table of cumulative infiltration

2.3 肥液浓度对双点源涌泉根灌土壤含水率分布的影响

入渗结束后，对清水入渗和不同肥液浓度（5、10和20 g/L）条件下，0～100 cm土壤含水率分布状况进行分析。测定位置分别为灌水器、交汇侧距灌水器12.5 cm和交汇面处（见图4）。

图4 灌水器处土壤含水率分布曲线Fig.4 The moisture curve at the emitter

灌水器下方垂直方向土壤含水率随土壤深度增加整体表现为先增加后减小的趋势，土壤深度20 cm处达最大值。肥液浓度分别为5、10和20 g/L时，土壤深度20 cm处土壤含水率分别较清水入渗显著（P＜0.05）增加了3.96%、7.42%和14.03%。相同深度的土壤含水率表现为随肥液浓度的增大而增大，土壤深度70 cm处肥液浓度为5、10和20 g/L的土壤含水率分别较清水入渗的土壤含水率显著（P＜0.05）增加了15.47%、42.12%和88.66%；当土壤深度大于70 cm时，肥液对土壤含水率的影响较小。

图5为交汇侧距灌水器12.5 cm处土壤含水率分布状况。由图5可知，灌水器交汇侧距灌水器12.5 cm处土壤含水率整体表现为先增加后减小，不同肥液浓度下的土壤含水率均在土壤深度20 cm处为最大值，在土壤深度20 cm处，肥液浓度5、10、20 g/L的土壤含水率分别较清水入渗显著（P＜0.05）增加了1.68%、5.49%、8.77%。另外，交汇侧距灌水器12.5 cm处的土壤含水率在土壤深度相同时表现为随肥液浓度的增大而增大；在土壤深度0～70 cm，肥液入渗条件下的土壤含水率较清水入渗的土壤含水率出现显著变化，随土壤深度的增加先减小后增加，在土壤深度70 cm处变化最显著，肥液浓度5、10、20 g/L的土壤含水率分别较清水入渗显著（P＜0.05）增加了19.02%、52.23%、68.53%；在土壤深度70～100 cm，肥液入渗条件下的土壤含水率较清水入渗的土壤含水率未出现显著变化；在土壤深度30 cm处，肥液入渗条件下的含水率较清水入渗的含水率之间无显著差异，其中肥液浓度5、10、20 g/L的土壤含水率分别较清水入渗增加了1.28%、4.81%、8.44%。

图5 交汇侧距灌水器12.5 cm处含水率分布曲线Fig.5 The moisture curve distance emitter 12.5 cm of the intersection side

图6为交汇面处土壤含水率分布状况。由图6可知，交汇面处土壤含水率整体表现为先增加后减小，不同肥液浓度下的土壤含水率均在土壤深度20 cm处达最大值，在土壤深度20 cm处，肥液浓度5、10、20 g/L的土壤含水率分别较清水入渗显著（P＜0.05）增加了2.09%、5.02%、6.69%。另外，交汇面处土壤含水率在相同深度时表现为随肥液浓度增大而增大；在深度0～60 cm处，肥液入渗条件下的土壤含水率较清水入渗的土壤含水率出现显著变化，在深度60 cm处变化最显著，其中肥液浓度5、10、20 g/L的土壤含水率分别较清水入渗显著（P＜0.05）增加了21.45%、42.00%、81.43%；在深度60～100 cm，肥液入渗条件下的土壤含水率较清水入渗的土壤含水率未出现显著变化；土壤深度30 cm处肥液入渗条件下的含水率较清水入渗的含水率无显著差异，其中肥液浓度5、10、20 g/L的土壤含水率分别较清水入渗增加了0.40%、1.69%、3.98%。整体来看，湿润区域的土壤含水率表现为随肥液浓度增大而增大。

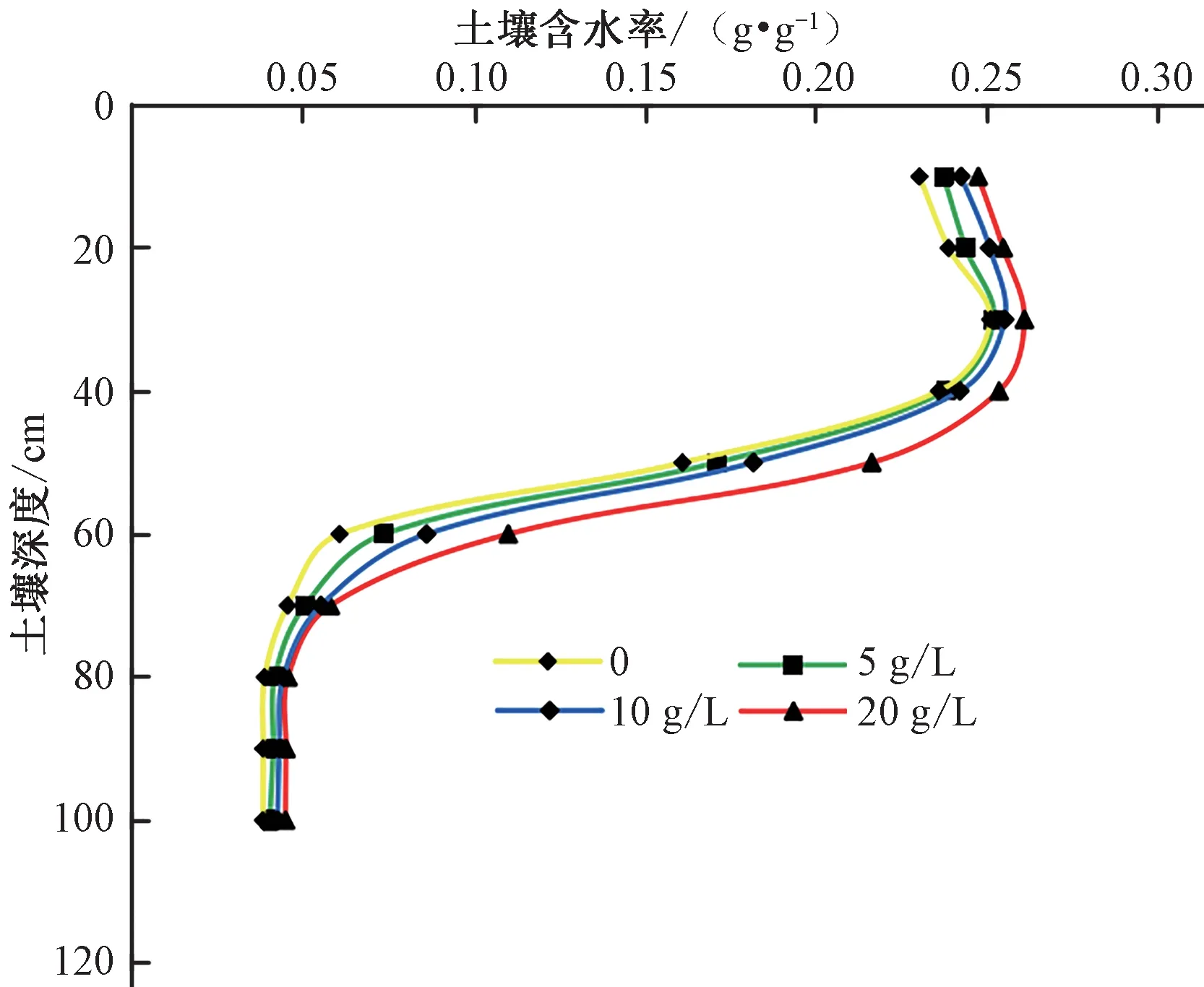
图6 交汇面土壤含水率分布曲线Fig.6 The moisture curve in intersection surface

2.4 涌泉根灌条件下双点源交汇入渗较单点源入渗的入渗特征分析

为进一步分析双点源交汇入渗特征，在相同肥液浓度下进行单点源入渗并进行对比。在双点源交汇入渗试验中根据2个灌水器湿润锋发生交汇现象的时刻，将入渗阶段分为自由入渗阶段和交汇入渗阶段。本次试验对湿润锋运移状况进行计时观察，其中10 g/L肥液浓度涌泉根灌双点源交汇入渗的湿润锋在入渗时间达到143 min时发生交汇。因此在10 g/L肥液浓度涌泉根灌双点源交汇入渗试验中，0～143 min为自由入渗阶段，143～300 min为交汇入渗阶段。图7为10 g/L肥液浓度条件下单点源入渗和双点源入渗的累积入渗量变化曲线。由图7可知，10 g/L肥液浓度条件下，在0～143 min单点源入渗和双点源入渗的累积入渗量变化曲线差异不大，在143～300 min双点源入渗累积入渗量较单点源入渗的有所减小，并且单点源入渗和双点源入渗的累积入渗量之间的差异随时间逐渐增大。

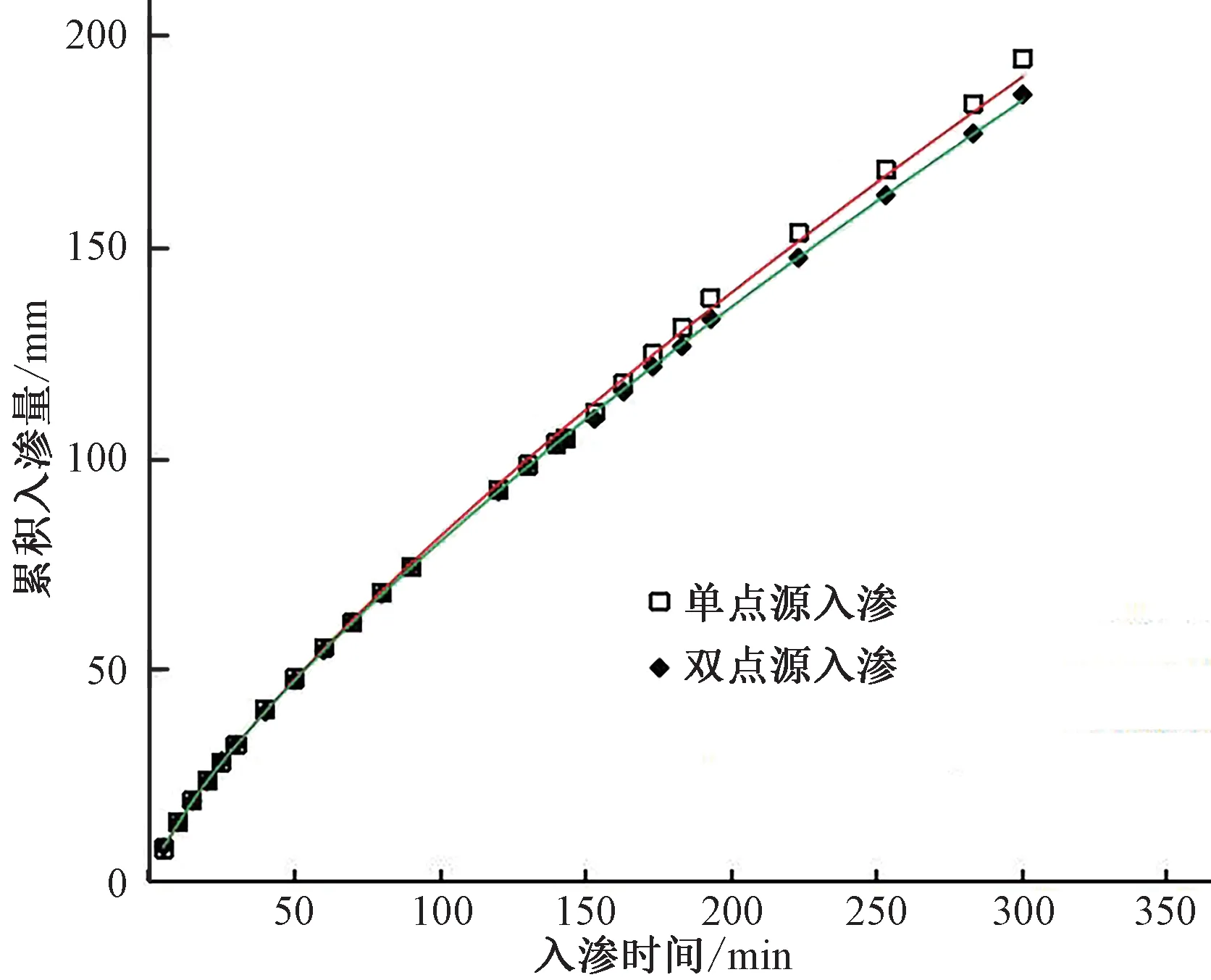
图7 涌泉根灌双点源入渗与单点源入渗累积入渗量曲线Fig.7 Cumulative infiltration curve of double point source infiltration and single point source infiltration in Bubbled-root irrigation

为量化分析涌泉根灌双点源交汇入渗条件下不同阶段累积入渗量特征，利用减渗量ΔI，对肥液浓度10 g/L双点源入渗交汇入渗阶段（143～300 min）的累积入渗量与单点源入渗相同时间阶段的累积入渗量进行对比分析。表3为肥液浓度10 g/L条件下143～300 min双点源入渗较单点源入渗的减渗量分析。

表3 双点源入渗交汇入渗阶段较单点源入渗的减渗量Tab.3 The infiltration reduction of double point source infiltration at intersection stage compared with single point source infiltration

经分析，减渗量随时间增加逐渐增大，减渗量与时间之间具有较好相关性。对减渗量ΔI与入渗时间进行拟合得：

式中：ΔI为减渗量，mm；t为入渗时间，min。

可以看出，涌泉根灌条件下双点源入渗交汇入渗阶段的累积入渗量与单点源入渗相同时间的累积入渗量符合幂函数关系。

对入渗结束后双点源入渗条件下交汇面处含水量与单点源入渗条件下距离灌水器相同位置处含水量垂直分布状况进行对比分析。图8为肥液浓度10 g/L条件下双点源入渗的交汇面处和单点源入渗距灌水器25 cm处含水率垂直分布状况。由图8可知，在土壤深度0～70 cm，双点源入渗的交汇面处土壤含水率明显大于单点源入渗距灌水器25 cm处土壤含水率，这主要是由于湿润锋发生交汇后，土壤水分运动在垂直方向受到基质势和重力势的共同作用，增强了水分向下运动能力，促进了土壤水分的积累。

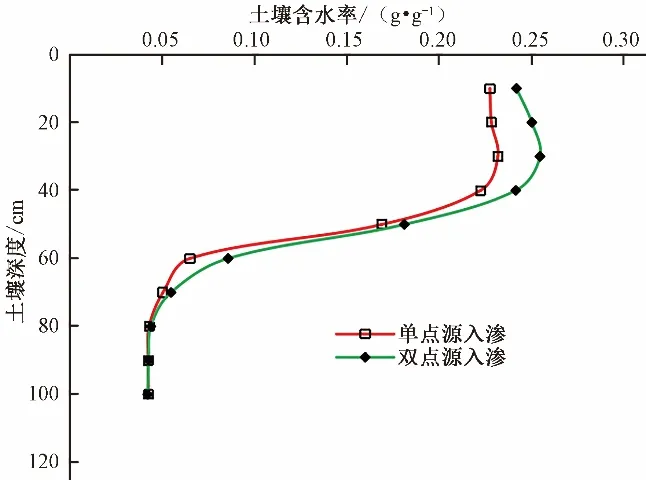
图8 双点源入渗交汇面处和单点源入渗相同位置含水率曲线Fig.8 Water content curve at the intersection surface of double point source infiltration and the same position of single point source infiltration

3 讨 论

涌泉根灌灌水技术对于缓解水资源短缺、提高水肥利用效率效果显著，尤其是在果树节水灌溉领域具有广阔的推广前景。涌泉根灌不同水肥条件对双点源入渗交汇面处土壤水分入渗特性、土壤含水率分布状况的影响，是进一步丰富涌泉根灌灌水技术要素的重要方面。大量研究表明[13-18]，涌泉根灌肥液入渗条件下累积入渗量随入渗肥液浓度的增大而增大，这是由于在肥液入渗过程中，土壤中带负电荷的胶体逐渐被肥液中的铵根离子中和，使土壤胶体之间排斥作用减弱甚至消失，进一步促使微小胶体形成团聚体，增加了土壤颗粒的粒径，改善了土壤结构，从而增强了土壤的入渗能力。但不同肥液浓度双点源入渗条件下累积入渗量变化的研究鲜有报道。本研究表明涌泉根灌双点源入渗条件下交汇面处的累积入渗量与入渗肥液浓度呈正相关幂函数关系，而相同肥液浓度下，在湿润锋交汇后的交汇入渗阶段双点源入渗的入渗量小于单点源入渗相同时间段的累积入渗量。这主要是由于涌泉根灌多向交汇入渗为充分供水条件下的空间三维入渗，在试验条件下，水分入渗过程中的土水势主要包括重力势、压力势和基质势等，土壤水分在土水势的驱动下运移；在涌泉根灌多向交汇入渗发生交汇后，入渗过程变为二维入渗，在水平方向，交汇界面两侧具有相同的土水势，水平方向的水流通量为零，该界面两侧不存在水势梯度，即水分不能通过零通量面，减弱了水分的水平侧渗，所以导致涌泉根灌多向交汇入渗量与自由入渗量存在较大差别，两者之间出现减渗现象，导致双点源入渗的累积入渗量较单点源入渗要小。本研究表明，双点源交汇入渗土壤含水率随肥液浓度的增大而增大，且在不同土层深度出，双点源入渗自由入渗测和交汇入渗侧含水率存在一定差异，在土壤深度0～70 cm时，肥液入渗条件下的含水率和清水入渗的含水率差异随土壤深度增加逐渐显著，且肥液浓度越大，土壤含水率差异变化越大，肥液浓度5、10、20 g/L的土壤含水率分别较清水入渗增加了15.47%、42.12%、88.66%，土层深度70～100 cm，肥液入渗和清水入渗条件土壤含水率差异逐渐减小。代智光等[24]研究了红壤区肥液浓度对涌泉根灌水氮运移特性的影响，结果表明，在同一土层深度范围内，土壤含水率与肥液浓度呈正相关关系，本研究表明肥液浓度对黄土区涌泉根灌双点源入渗条件下土壤含水率分布的影响同样具有正相关关系。这主要是由于在肥液入渗过程中，施入的尿素中含有大量铵态氮，其自身携带的正电荷与土壤胶体中大量的负电荷发生反应，促进土壤大团聚体的形成，有利于改善土壤水分的再分布特性。

4 结 论

（1）肥液促进了双点源涌泉根灌的土壤水分入渗能力，累积入渗量随肥液浓度增加而增加。

（2）双点源涌泉根灌累积入渗量可利用Philip模型和Kostiakov模型进行拟合，肥液增加了土壤吸渗率及初始入渗速率，土壤入渗能力的衰退速度有所延缓。

（3）肥液提高了双点源涌泉根灌的土壤含水率，且随肥液浓度增大显著增大。

（4）双点源涌泉根灌比单点源的累积入渗量有所减小，且随时间增加，差异逐渐增大。