滴灌系统压差式施肥罐施肥性能研究

杨 欣，王文娥，胡笑涛，孟庆海

(西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

0 引 言

现在农业生产中，滴灌技术广泛应用于温室大棚及经济作物灌溉，具有节水增产等优点，同时还可实现水肥一体化，将灌水和施肥相结合不但可以提高水肥资源利用率，降低农业面源污染，还具有节省劳动力、提高灌溉自动化的优点，在我国具有广阔的应用前景。滴灌系统常用的施肥装置按照其工作原理分为压差式、吸入式和注入式3种[1]。其中，压差式施肥罐因其成本低、维修简单、不需要外加动力等优点，是目前使用最为广泛的施肥装置[2]。

压差式施肥技术主要是通过调控施肥罐前后压差将肥液溶液带入滴灌管道，再通过滴灌管、滴灌带等灌水器件，以小流量的形式灌入到土层中[3]。由于施肥罐中的肥料在灌溉施肥前按照施肥量加入，在灌水施肥的过程中，肥液浓度持续衰减[4,5]，这个变化过程直接影响施肥质量和系统运行的稳定性。封俊等人[4]的研究表明，施肥罐容积、压差和施肥量是影响施肥罐输出肥液浓度衰减的主要因素。孟一斌等[6]研究指出施肥罐前后压差越大，肥液浓度衰减的速度越快，施肥的时间就越短。但对于影响压差式施肥罐肥液浓度变化过程和影响因素的定量关系研究还不深入，未建立施肥罐出口出肥液浓度衰减过程的通用模型。

为探索影响滴灌压差式施肥罐施肥效果的影响因素，本研究通过控制施肥罐前后压差和施肥量，对施肥罐出肥口肥料浓度随时间的变化过程进行了试验研究，建立了压差式施肥罐浓度变化的数学模型，为滴灌施肥系统能合理运行和设计提供建议。

1 材料与方法

试验在西北农林科技大学的农业部旱区农业节水重点开放实验室灌溉大厅内进行，试验布置如图1所示。该试验通过实验室灌溉大厅中央水泵进行供水，通过主管道(Φ63 mm)进水阀门2控制该系统的进水量，流量计3测定试验期间通过的总流量Q，通过调节阀门2和5的开度来调节压力表4和6(0.25 MPa，0.25级)，用来调控实验装置施肥罐前后两端的压力差。试验选用由石家庄元润农业机械科技有限公司生产的容积为13 L的压差式施肥罐，肥料选用大田常用的水溶性硫酸钾(K2SO4，K2O≫50%，上海汉合生产)作为本次实验的试验肥。

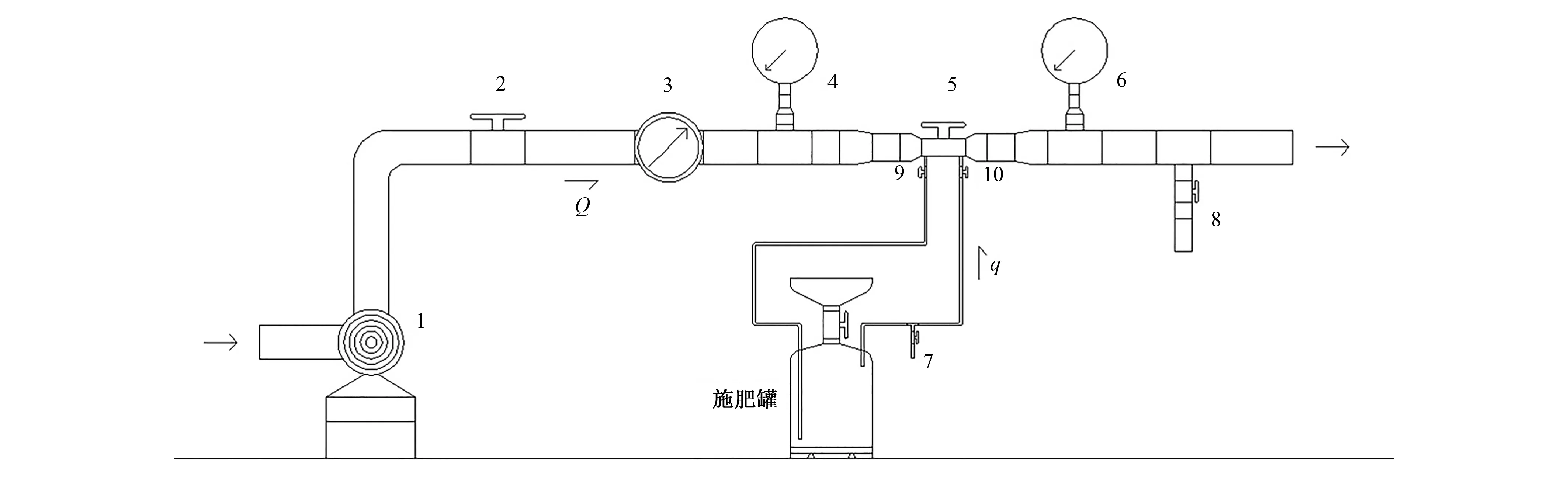
1-水泵；2-阀门(Φ63 mm)；3-流量计；4-压力表1；5-阀门(Φ32 mm)；6-压力表2；7-施肥罐出肥取样点；8-支管取样点；9-入水阀门；10-出水阀门图1 压差式施肥罐试验装置

试验通过控制不同施肥量和压差条件对施肥罐出肥口的肥料浓度进行检测，试验中施肥量选用1.0、1.5、2.0 kg 三个水平，施肥罐两头压差选用0.03、0.06、0.09、0.12、0.15 MPa五个水平。实验中将施肥罐出口压力P2控制为0.01 MPa，共进行11组压差与施肥量组合的试验，每个组合重复3次。如表1所示。

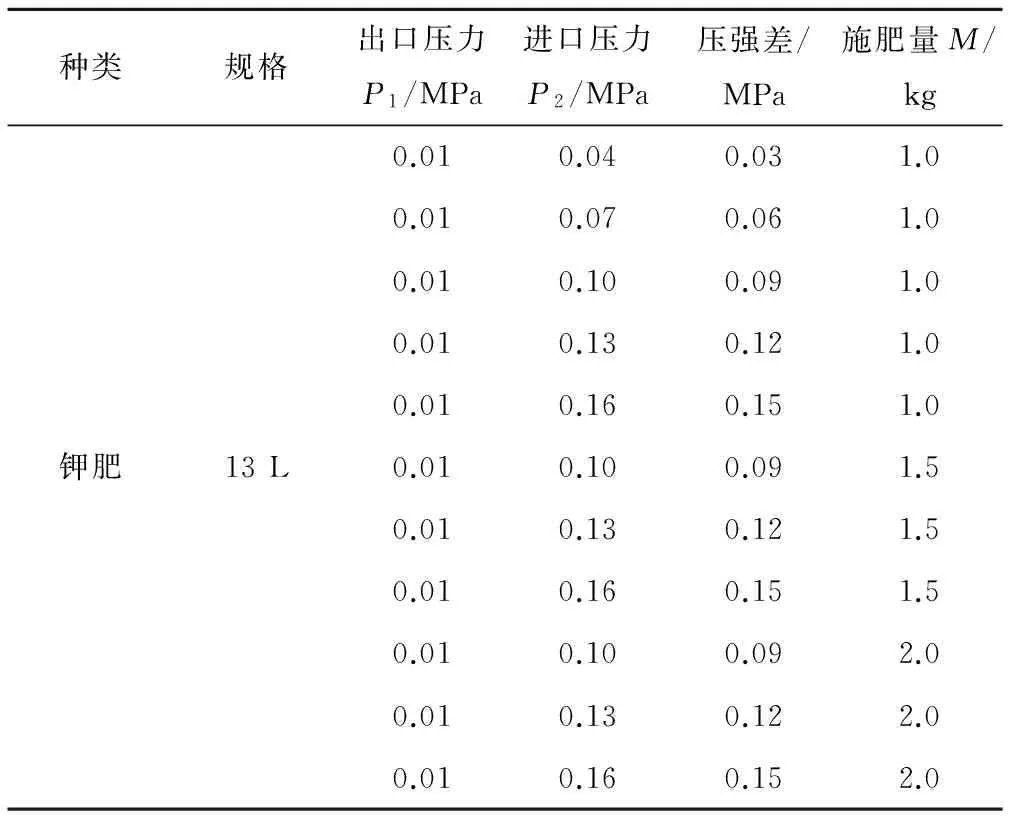
表1 试验因素的变化范围

试验开始前先称取一定量的钾肥加入施肥罐，通过施肥罐进水管注水，与实际农田滴灌施肥过程一致。待罐内注满水后，关闭施肥罐进水口，此时测得的肥液浓度即为系统的初始浓度。通过调压阀门2和5调节施肥罐进水口和出水口处的管道压力，试验过程中施肥罐出水口的管道压力恒定为0.01 MPa。待实验准备就绪，通过流量计读出初始流量，打开施肥罐进水口和出水口，同时开始计时。在实验开始后的固定时刻1、2、3、4、6、8、10、12、14、16、20、30、40、50、60、75、90、105、120 min取施肥罐出水管7和支管8处肥液样本100 mL，采用电导率仪[上海雷磁电导率仪DDSJ-308F，测量范围(0～199.9 mS/cm)，精度±0.5%，温度补偿(-5.0～110.0)℃]测得其电导率，当测得的电导率的值近似等于当日测得的纯水电导率时，可认为肥料全部溶解，并停止计时，读取流量计的度数，试验结束。

通过使用试验当日标定的肥液浓度与电导率的关系式(1)将肥液样本的电导率转化成浓度：

C=aEC-b

(1)

式中：C为肥液浓度，g/L；EC为肥液电导率，mS/cm；a、b为系数。

为了提高肥液浓度与电导率转换关系的精确度，需实验周期内每日配置定浓度肥液时设定3个不同的水平，即：10 g/L≤C≤50 g/L、1 g/L≤C≤10 g/L、0 g/L≤C≤1 g/L。图2给出了一次试验时肥液电导率和对应浓度的关系图，具有很好的线性关系。根据关系图通过拟合分析得到电导率EC与对应浓度C关系式(1)。由于电导率受水温等影响[7]，肥液浓度与电导率的关系式中参数a、b不是固定值，需根据当日配定肥料溶液，测定对应电导率，确定关系式(1)中的参数。

图2 肥液浓度与电导率的关系

2 结果与分析

2.1 施肥罐作用压差与通过流量的关系

调节施肥罐进出口压差可以控制通过罐体的清水流量，流量不同时溶解肥料的量、肥液浓度及肥料溶解过程均不同，进而影响到进入滴灌系统支管的肥液浓度和施肥过程。试验中分别在施肥罐出水口以及支管上设置肥液取样点。已知Q，通过计算得知对应的CQ和Cq，根据浓度的定义和组分质量守恒定律可以由公式(2)计算对应q：

CQQ=qCq

(2)

式中：CQ为主管道平均浓度，g/L；Cq为施肥罐出水口平均浓度，g/L；Q为主管道平均流量，m3/min；q为施肥罐出水口平均流量，m3/min。

施肥量出水口平均浓度与主管道平均浓度之比与压差的关系如图3所示。

通过回归分析，得出施肥罐的压差与流量比的关系式(3)以及确定系数。

q/Q=2.461ΔP1.657(R2=0.986)

(3)

式中：q为施肥罐出水口流量，m3/min；Q为主管道流量，m3/min；ΔP为施肥罐前后压力差值，MPa。

图3 通过施肥罐的流量与压差的关系

由公式(3)以及图3可以看出，通过施肥罐的流量与施肥罐进水口与出水口处主管道上的压力差呈幂函数增长，且相关程度极高。

2.2 肥液浓度随时间变化规律及影响因素分析

由于施肥罐开始施肥前罐内先充满水，肥料能够比较充分的溶解，肥液浓度最高，随着施肥过程的进行，施肥罐内的肥料不断被水稀释，浓度将逐渐降低。肥液浓度的均匀度影响作物根系对肥料的吸收，需要探明施肥罐出口肥液浓度随时间的变化规律。初始肥液浓度与施肥量在施肥罐内的溶解大小情况有关，还会受到水温等影响，即使是同施肥量的情况下，初始肥液浓度尽管相差很小但也不完全相同，所以用相对浓度(取样时刻t的肥液浓度与t=0时的初始肥液浓度比值的百分值)来表示施肥罐出水管的肥液浓度的变化，图4给出容量为13 L规格的压差式施肥罐加入1.0、1.5、2.0 kg的施肥量，在不同压差情况下施肥罐出口处相对肥液浓度随时间变化的过程曲线。

由图4可看出，施肥罐出口肥液相对浓度随时间持续降低，在前10 min肥液浓度急剧下降，之后降低较为平缓，20 min后浓度趋于稳定。以施肥量1.0 kg为例，t=1、4、10、14、20和30 min时，压差0.09 MPa下的相对肥液浓度值为83.43%、40.48%、11.42%、7.08%、3.47%和1.35%。也就是说，在一次施肥过程中肥液浓度随时间降低的过程很不均匀，尤其初始的20 min，将影响到田间灌溉施肥均匀性。

图4 施肥罐出口肥液相对浓度随时间的变化规律

当施肥罐内装入施肥量一定、施肥罐作用压差越大时，通过的流量越大，即罐内流速越大，进而加快了肥料的溶解，例如图4(a)施肥量为1.0 kg、施肥历时t=8 min时，压差分别为0.06、0.09、0.12 MPa工况下，相对肥液浓度分别为23.15%、15.12%、14.50%，可知施肥量相同时，在同一时刻，压差越大，相对肥液浓度越小。

当施肥量不同，相同压差条件下，相同时刻施肥量越大，相对肥液浓度越大，例如压差为0.12 MPa,施肥时间t=8 min，施肥罐内装入肥料量分别为1.0、1.5、2.0 kg时，其对应的相对肥液浓度值为15.94%、23.73%、33.06%。

但是施肥量与通过的施肥罐流量需要配合适当，这样才能使肥料在一定施肥运行时间内充分溶解、施入田间。在图4(a)中，施肥罐内装入肥料量为1.0 kg、压差0.03 MPa时，t=1 min时相对肥液浓度为40.66%，肥料溶解度低，原因是肥料放置在罐体底部，压差较小时进入罐体的水流流量小，流速低，水流与底部肥料接触不充分，造成溶解度低；相同装入肥料量情况下，当压差0.15 MPa时，相对肥液浓度变化与其他工况不同，t=1 min时相对肥液浓度仅有3.52%，然后迅速衰减，在t=3 min时接近0，浓度变化过程很不稳定；其原因是压差相对过大时，通过施肥罐流量也大，肥料被快速冲走，施肥过程中肥液的均匀性过低；施肥2.0 kg，压差为0.09 MPa和t=120 min时，相对肥液浓度值为6.4%，仍是一个相对较高值，施肥罐内肥液输送需要较长时间。所以在过高、过低施肥量和小压差条件下，施肥罐不易于施肥。

对不同条件下施肥罐出口肥液浓度随时间的变化过程可按照关系式(4)进行拟合：

C/C0=e-β t

(4)

式中：C为t时刻的肥液浓度，g/L；C0为肥液的初始浓度，g/L；β为拟合参数。

施肥罐出口肥液的初始浓度C0及参数β与施肥罐的容积、作用压差、肥料种类及装入肥料量、水温等因素相关。

2.3 施肥总历时影响因素分析

滴灌系统运行时，一般先滴清水，可以把管道及滴头内的残余物质冲出，大约运行半小时后开始施肥，施肥结束后再滴半个小时清水，使管道和滴头内的肥液全部施入田间，并冲洗系统残余物质，防止堵塞。一般认为肥液相对浓度低3%是可以认为施肥结束[8]。从图4可以看出当施肥量为1.0 kg，压差为0.03 MPa、0.15 MPa和施肥量为2.0 kg，压差为0.09 MPa条件下，运行时间t=60 min时，肥液相对浓度仍然大于3%，运行时间达到120 min时，肥液相对浓度才接近3%，施肥总历时较长。其他试验条件下，运行时间t=60 min时，肥液的相对浓度基本在0～1.35%范围内，肥液浓度接近0，可认为施肥结束，这样的运行时间与微灌系统灌溉及冲洗过程能够很好地配合，较为适宜。

滴灌系统一次运行时间根据灌水量和滴头流量确定，一般在2 h左右，所以施肥总历时不能过长，否则将影响整个系统的运行，很有必要确定施肥总历时的影响因素及其之间的关系。Amos Teitch曾总结旁通施肥罐内肥液浓度衰减的变化规律，给出公式 ：

T=4V/Qt

(5)

式中：T为施肥结束时间，s；V为施肥罐体积，m3；Qt为通过施肥罐的流量，m3/s。

公式可理解为，当单位时间内通过施肥罐的水体体积达到4倍的施肥罐体积时，可认为施肥基本结束[9]。由试验计算可知每次通过施肥罐的流量，通过公式(5)计算出对应施肥结束时间，见表2。由表2可知，施肥结束时间的实际值与计算值偏差很大，偏差率高达84.4%，可见该经验公式并不一定适用于各种压差式施肥情况，需考虑到别的影响因素。

从开始施肥到施肥罐出口肥液浓度衰减为零(施肥结束)的历时是微灌施肥灌溉系统运行管理的重要指标，与系统冲洗开始时间密切相关。图5为试验中各工况施肥结束时间与施肥质量和施肥压强差的关系，通过回归分析建立施肥历时Tc=0(min)与施肥量M、压差ΔP的函数关系式。

TC=0=3.594M1.18ΔP-1.03(R2=0.901)

(6)

式中：TC=0为施肥历时，min；M为施肥量，kg；ΔP为施肥罐作用压差，MPa。

表2 施肥结束时间实际值与计算值

图5 不同施肥量时施肥结束时间与压差的关系

由式(6)和图5可以看出，肥液浓度为零的时间Tc=0随施肥量的增大而增大，随压差比的增大而减小。通过对比图5实测值与式(6)模拟值的拟合情况，两者具有较好的一致性。通过计算施肥量1、1.5、2 kg的剩余标准差，其对应值为3.4%、2.69%和2.74%。因此该式(6)可用来估算不同情况下施肥罐的施肥结束时间。

3 结 语

(1)压差式施肥罐出口流量与施肥罐作用压差呈幂函数关系，流量随作用压差的增加而增加。

(2)压差式施肥罐出水口肥液浓度随时间呈指数函数关系持续减小，t=10 min前急剧衰减，t=20～30 min后浓度趋于稳定；肥液浓度与肥料量、作用压差、肥料的溶解度相关，在过高、过低施肥量和小压差条件下，滴灌系统不易获得均匀的肥液分布。容积13 L的压差式施肥罐使用钾肥时，适宜施肥量在1.0～2.0 kg之间，压差在0.06～0.15 MPa之间。

(3)施肥量和压差式施肥罐作用压差是制约施肥总历时的主要因素，通过建立施肥结束时间与压差、施肥量的变化关系，可对系统冲洗时间做出参考。在合理的施肥量和作用压差条件下，施肥总历时与施肥量和作用压差呈幂函数关系式。

[1] 韩启彪,冯绍元,黄修桥,等.我国节水灌溉施肥装置研究现状[J].节水灌溉,2014,233(12):76-79,83.

[2] 王 成.滴灌系统常用施肥装置操作要点及优缺点分析[J].现代农业科技,2015,647(9):234,238.

[3] 杨晓宏,严程明,张江周,等.中国滴灌施肥技术优缺点分析与发展对策[J].农学学报,2014,35(1):76-80.

[4] 封 俊.压差式喷灌施肥装置的研究[J].农业工程学报,1991,7(2):107-113.

[5] 陈 剑,吕 新.滴灌棉田压差式施肥罐注肥均匀度研究与分析[J].节水灌溉,2011,185(1):62-64.

[6] 孟一斌,李久生,李 蓓.微灌系统压差式施肥罐施肥性能试验研究[J]. 农业工程学报,2007,114(3):41-45.

[7] 顼魁辰,潘勇飞.电导率测量的影响因素及电导率、pH值异常与金异常的关系[J].黄金地质科技,1993,35(1):44-51.

[8] 韩启彪,李 浩,冯绍元,等.CFD模拟在压差施肥罐浓度衰减研究中的应用初探[J].灌溉排水学报,2015,34(12):81-84.

[9] Burt CM, O′Connor K, RuehrT. Fertigation[M].San Luis Obispo, Calif.:Irrigation Research and Training Center, California Polytechnic University,1995.