不同初始含水率下风沙土地下渗灌水分运移特性研究

马宏秀，孙 权*，鲁海涛，马文礼，蒋 鹏，张晓娟，蔡崭红，贾登成

（1.宁夏大学 农学院，银川 750021；2.宁夏农垦农林牧技术推广服务中心，银川 750011；3.宁夏农垦国营简泉农场，宁夏 石嘴山 753299）

0 引 言

【研究意义】西北地区虽然光热资源丰富，农业生产潜力巨大，但因缺水且缺乏养分，仅在有水源灌溉的区域零星分布着绿洲农业区。地下渗灌是一种地下微灌形式，是指在低液压条件下，使灌溉水（含可溶性养分）通过埋设在每株作物根系范围内的渗水管道，其管壁上分布有均匀的微孔，水分由内向外呈发汗状渗出，以滴渗方式湿润作物根系层周围土壤，即直接向每株作物根系适时适量地供水、供养的一种节水增产的灌溉技术方法[1]。该技术比地表滴灌更进一步减少了水分蒸发与肥料运移的损失，达到良好的节水、节肥效果，从而对干旱半干旱地区水肥资源的高效利用更具有现实意义。

【研究进展】土壤入渗是土壤水分的形成、转化与消耗的动态变化过程[2]，涉及土壤水分再分布、蒸发以及离子迁移等多方面[3]。土壤水分入渗受土壤体积质量、孔隙度等影响较大[4-5]，其中，土壤初始含水率作为重要的土壤物理性质，主要通过土壤湿润体内平均土水势梯度来影响土壤水分入渗过程[6]。康金林等[7]通过室内模拟土柱试验研究指出，均质红壤入渗能力与土壤初始含水率负相关，湿润锋运移速率随初始含水率的增大而增大。曾辰等[8]通过研究初始含水率对砂黄土和塿土的线源入渗特征的影响表明，2 种类型土壤的累积入渗量与初始含水率为二次函数关系。介飞龙等[9]基于HYDRUS 模型研究不同初始含水率对膜孔灌湿润体的影响，结果表明该模型优于Kostiakov 等传统入渗模型。然而，不同条件下初始含水率对土壤水分入渗过程影响不同，地下渗灌是一种利用土壤吸水作用发挥效能的被动供水方式且可以根据土壤初始含水率调节出水流量，因此，初始含水率对地下渗灌入渗特性有较大的影响[10]。【切入点】受地下渗灌管管材特质与承压特性的限制，地下渗灌技术尚在初始应用阶段，目前对不同初始含水率条件下地下渗灌入渗机制的研究较少。【拟解决的关键问题】为此，以西北主要土壤类型风沙土为对象，基于新型地下渗灌技术分析不同初始含水率条件下土壤水分入渗特征，以期为地下渗灌技术推广提供参考。

1 材料与方法

1.1 供试土壤

试验土壤风沙土于2022 年8 月取自宁夏银川市金凤区良田镇植物园二村，取土深度为0～30 cm，将取得不同土层深度土壤自然风干后，清除杂质，均匀混合，过2 mm 筛备用。土壤基本物理性质见表1。

表1 供试土壤物理性质Table 1 Physical properties of the soil tested

试验前按设计含水率（质量含水率）加水，混合均匀后用塑料布覆盖静置24 h，次日开展入渗试验，待土壤水分分布均匀后，按照设计土壤体积质量1.47 g/cm3，每5 cm 为1 层分层装入试验土箱。

1.2 试验材料和装置

试验所用渗灌管由南京德水节能科技有限公司提供，其主要参数为：内径13 mm，壁厚1.5 mm，外表面布满微孔，工作运行压力0.06 MPa，稳定压力下额定流量为6 L/（h·m）。

试验装置由土箱和供水装置组成（图1），试验土箱为1 cm 厚有机玻璃制成，箱体规格为200 cm×200 cm×100 cm（长×宽×高），其底部均匀分布有直径0.2 cm 的小孔便于通气。供水装置主要由供水箱、回水箱、水泵、压力表、流量计等组成。土层总高度100 cm，渗灌管埋深50 cm。为了真实模拟田间应用情况，箱内安插2 条间距为100 cm 的渗灌管，渗灌管长度与土箱长度均为200 cm，进口端连接供水系统，出口端封闭。供水箱和回水箱的箱体上标有刻度，用于测定和校核供水流量。水泵内设置电位调速器，以便调节供水压力。

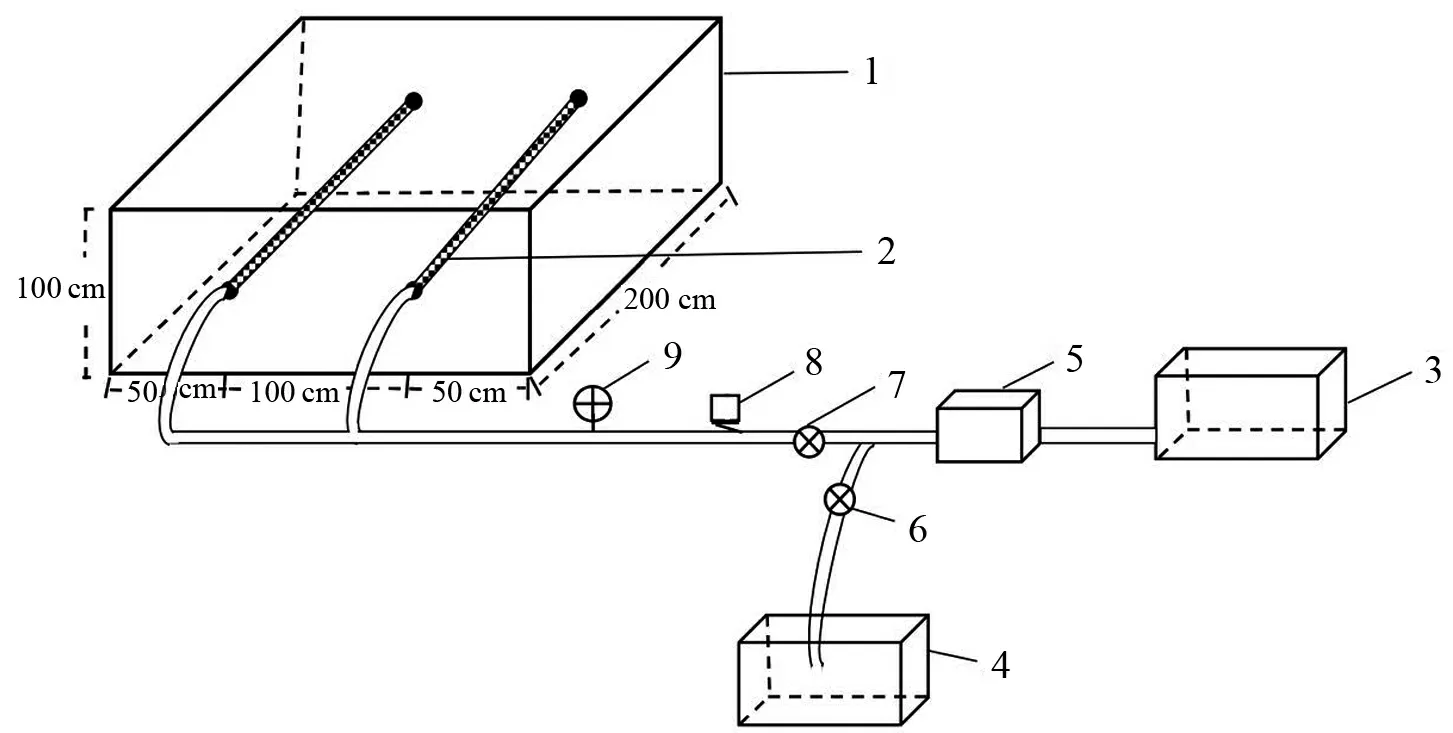
图1 试验装置图Fig.1 Diagram of the test device

1.3 试验设计

根据前人[11]关于沙土含水率分布情况的研究，试验设置3 个不同初始含水率水平（土壤自然风干时的含水率），分别为5.1%、11.5%、16.8%，为排除土壤水分蒸发的影响，表层用塑料膜覆盖，每组试验设置4 次重复，选取平均值进行数据分析。

试验开始后，记录不同时刻湿润锋的轮廓和灌水流量。在最初入渗0.5 h 内，分别在2、5、10、15、30 min 用卷尺测量出湿润体各向湿润锋运移距离，0.5 h 之后每隔30 min 观测1 次；采用L99-TWS-3 型土壤水分记录仪测定土壤水分，将传感器预先埋设在水平距管10、20、30、40、50 cm 处，埋设深度在10、20、30、40、60、70、80、90、100 cm 处，长期连续监测，测定前用烘干法测定含水率校正仪器。本试验设置单次灌水量为600 m3/hm2，即连续渗灌10 h 后，停止供水。

1.4 入渗模型拟合与评价指标

本研究选取Kostiakov、Philip、Horton 和通用经验型共4 种模型分别对入渗过程进行模拟，并对各模型拟合结果进行评价。

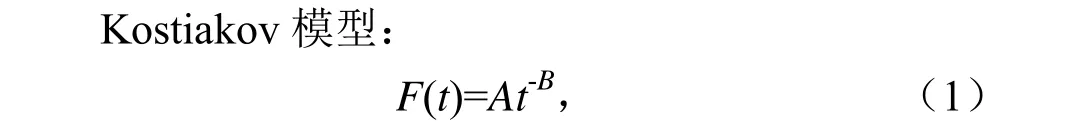
式中：F(t)为入渗速率（cm/min）；A和B为模型参数；t为入渗时间。

Philip 模型：

式中：S为稳定入渗率（cm/min）；V为模型参数。

Horton 模型：

式中：F0为初始入渗率（cm/min）；Fi为稳定入渗率（cm/min）；b为模型参数。

通用经验模型：

式中：m、n、k为经验参数。

1.5 累积入渗量拟合

选择幂函数对累计入渗量变化进行拟合：

式中：Z为累计入渗量；K为入渗系数；a为入渗指数。

1.6 克里斯琴森均匀系数

灌溉均匀度计算式为：

式中：CU为灌溉均匀度（cm3/cm3）；θ̅为湿润体平均含水率（cm3/cm3）；θi为第i节点处土壤含水率（cm3/cm3）；N为湿润体选取节点数。

1.7 数据处理与分析

采用Microsoft Excel 2016、Sigmaplot 12.5 软件处理数据及制图，运用SPSS 18 中的LSD 法进行方差分析，数据处理显著水平为0.05。

2 结果与分析

2.1 初始含水率对湿润锋运移的影响

2.1.1 湿润体形状变化特征

为了方便观测，以湿润体1/2 横剖面为研究对象。图2 为不同初始含水率对应的湿润锋动态变化过程，X为水平距离，Y为土层深度，坐标原点（0，0）为渗灌管所在位置，湿润锋以渗灌管位置为中心向外缓慢运移。选取不同灌溉时间湿润体水平移动半径R，垂直向下移动距离D，垂直向上移动距离L描述湿润体的形状和大小。由图2 可知，随着初始含水率的增大，湿润体横剖面形状越来越接近椭圆形，初始含水率对地下渗灌下湿润体形状具有较大影响。当初始含水率为5.1%时，R∶L∶D从1∶0.8∶1.2 逐渐变为1∶0.8∶1.25；初始含水率为11.5%时，R∶L∶D从1∶0.63∶1.25 逐渐变为1∶0.64∶1.22；初始含水率为16.8%时，R∶L∶D从1∶0.69∶1.48 逐渐变为1∶0.67∶1.43。随着灌水时间的延长，不同方向的湿润锋运移速率无显著差异，但随着初始含水率的增加，湿润锋垂直向上的扩散速率相对降低，而垂直向下的扩散速率相对增大。

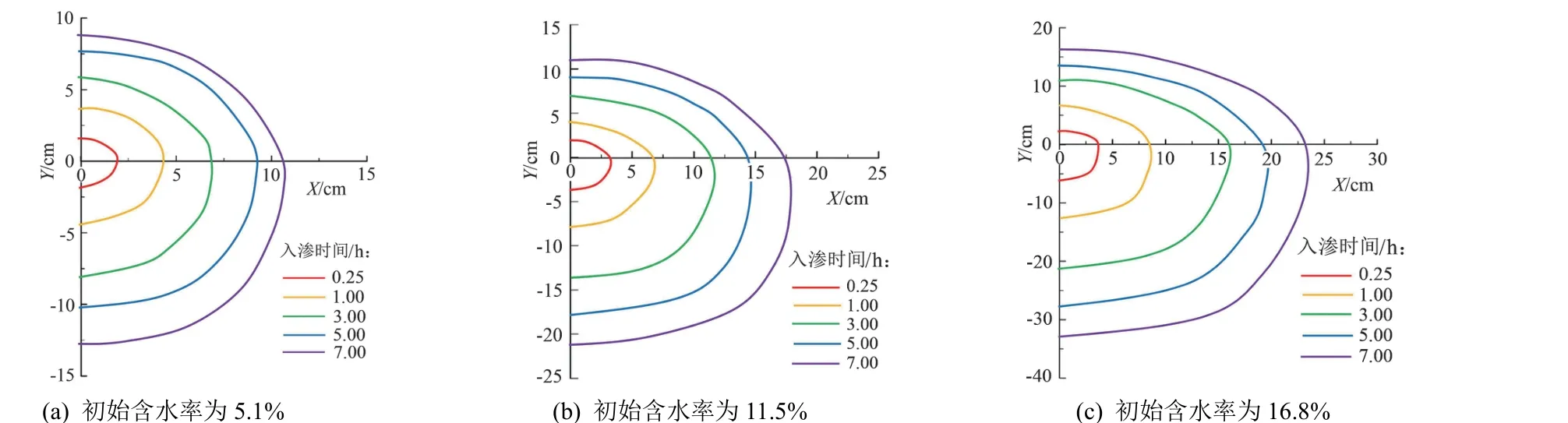
图2 湿润体动态分布Fig.2 Dynamic distribution of moisturites

2.1.2 湿润锋运移速率

图3 为初始含水率对湿润锋运移速率的影响。由图3 可知，不同初始含水率下湿润锋运移速率均呈下降趋势，随着灌水时间的增加，湿润锋运移速率逐渐趋于稳定。湿润锋在不同方向的推进速率均随初始含水率的增大而增大，原因是在初始含水率较高的条件下，土壤较快达到饱和状态，下渗率趋于稳定，然后在毛管水和重力水的作用下渗透移动，湿润锋运移速率相对较快[12]。初始含水率5.1%、11.5%、16.8%的垂直向上的平均扩散速率为1.45、1.86、2.54 cm/h，垂直向下的平均扩散速率为2.28、3.57、5.40 cm/h，水平方向的平均扩散速率为1.75、2.96、3.90 cm/h，说明初始含水率对垂直向下的运移过程影响最大，对水平方向的运移过程影响程度最小。

图3 初始含水率对湿润锋运移速率的影响Fig.3 Effect of initial water content on wetting front migration rate

2.2 初始含水率对累计入渗量和入渗率的影响

由图4 可知，在前15 min，各处理累计入渗量无明显差异，随着时间推移，同一时刻下初始含水率越大，累计入渗量越小，变化趋势越平缓。为了进一步定量分析初始含水率对地下渗灌入渗性能的影响，利用式（5）对不同初始含水率累计入渗量和入渗时间进行拟合，结果见表2。由表2 可得，累计入渗量和入渗时间符合幂函数关系，随着初始含水率的增加，入渗系数K呈减小趋势，而入渗指数a逐渐增大，相关系数均能达到0.99 以上。

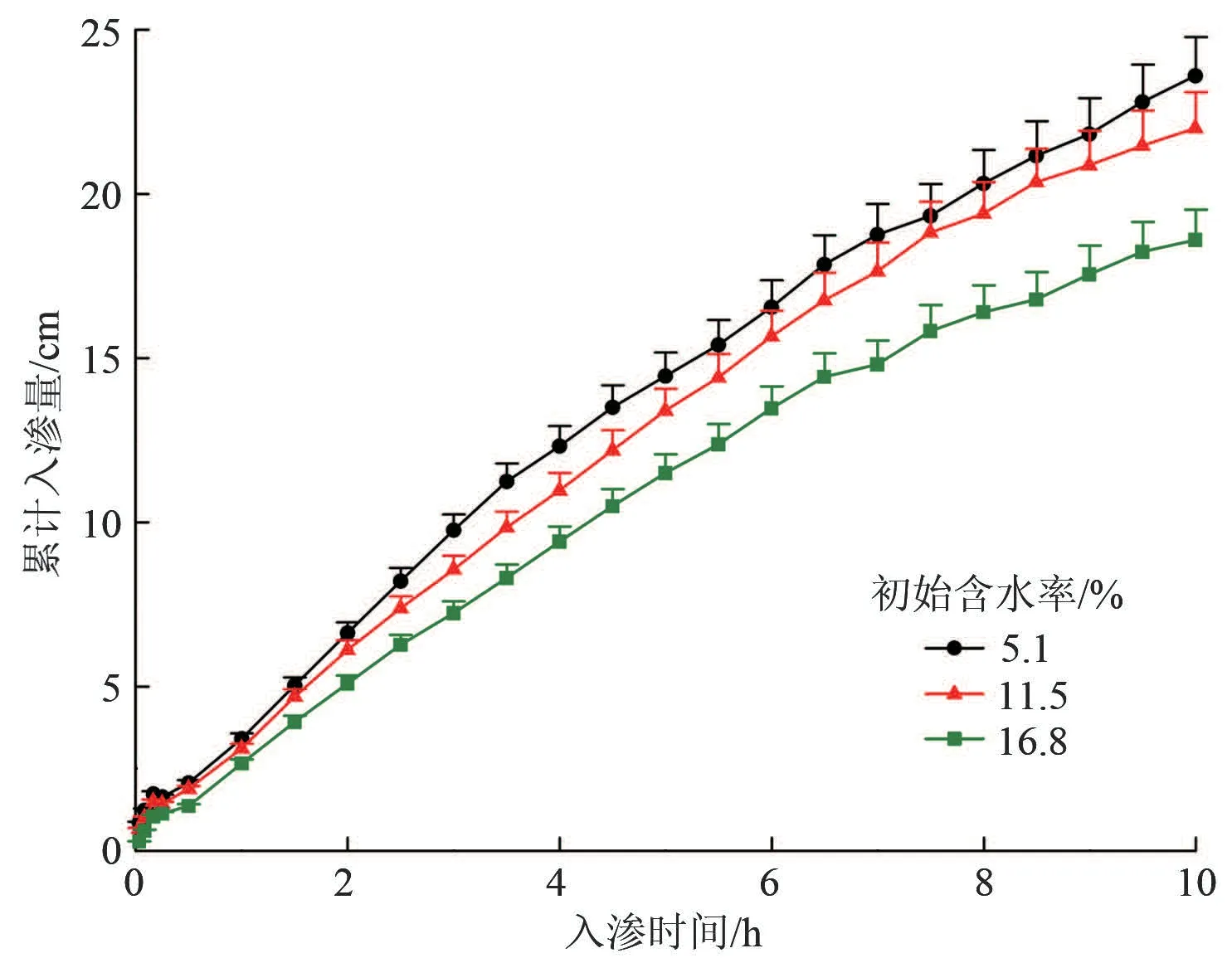
图4 初始含水率对累计入渗量的影响Fig.4 Effect of initial water content on cumulative infiltration

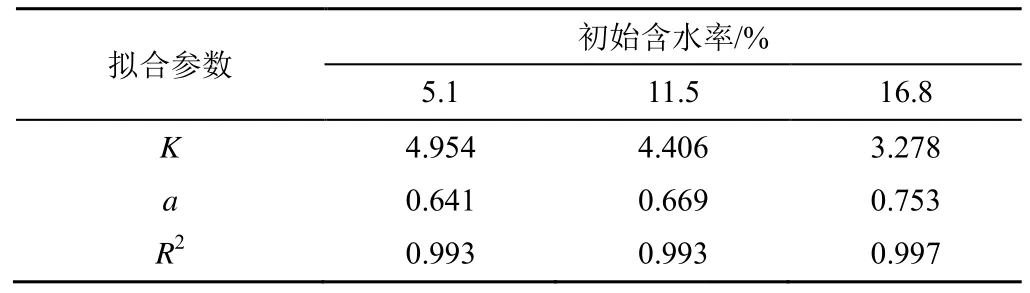
表2 累计入渗量与入渗时间拟合结果Table 2 Fitting results of cumulative infiltration and infiltration time

由图5 可知，不同初始含水率的平均入渗率随着入渗时间的延长均呈下降趋势，30 min 后均趋于平缓，达到稳定入渗阶段。初始含水率越高，入渗速率越小，入渗曲线较为平缓，到达稳定入渗速率的时间越短。原因是随着初始含水率的增加，入渗初期的土壤水吸力减小，平均入渗速率变化不大[13]。

图5 初始含水率对平均入渗率的影响Fig.5 Effect of initial water content on average infiltration rate

2.3 风沙土入渗过程模型拟合

表3 为不同初始含水率的入渗模型拟合结果。由表3 可以看出，不同入渗模型对土壤入渗过程的拟合结果有所差异。Kostiakov 模型回归结果R2为0.561～0.911，平均值为0.783，该模型在高初始含水率条件下的入渗精确度较低；采用Philip 模型回归结果R2为0.533～0.992，平均值为0.785，S值为0～0.013，对稳定入渗速率的拟合精度不够，且在高初始含水率条件下拟合效果较差；Horton 模型回归结果R2为0.917～0.956，平均值为0.943，对不同处理入渗过程的模拟效果均较好；通用经验模型中R2为0.897～0.944，平均值为0.923，参数m、n分别表征稳定入渗率和初始入渗率，参数k代表入渗速率随时间减小的程度，可以看出，随着初始含水率的增大，m呈增加趋势，而n呈减小趋势，与实测值不符。综上可知，4 种模型中对土壤入渗过程拟合适用性较好的是Horton 模型，其次为Kostiakov 模型、Philip 模型和通用经验模型。

表3 不同初始含水率的入渗模型拟合结果Table 3 Fitting results of infiltration models with different water content

2.4 初始含水率对湿润体水分再分布的影响

2.4.1 对湿润体垂直方向水分再分布的影响

灌水结束后，不同方向的湿润锋在渗透压和重力势等作用下会继续扩散和运动[14]。如图6 所示，坐标（0，50）点为渗灌管所在位置，初始含水率5.1%、11.5%、16.8%处理土壤含水率均随土层深度的增加呈先增大后减小，最后趋于稳定的趋势。在表层土壤中湿度较小，说明地下渗灌减少了土壤水分的地表蒸发，将水分储存在深层土壤，提高了水分利用效率[15]。但同时也需要注意初始含水率过高时深层土壤中平均含水率的变化，以免发生渗漏。

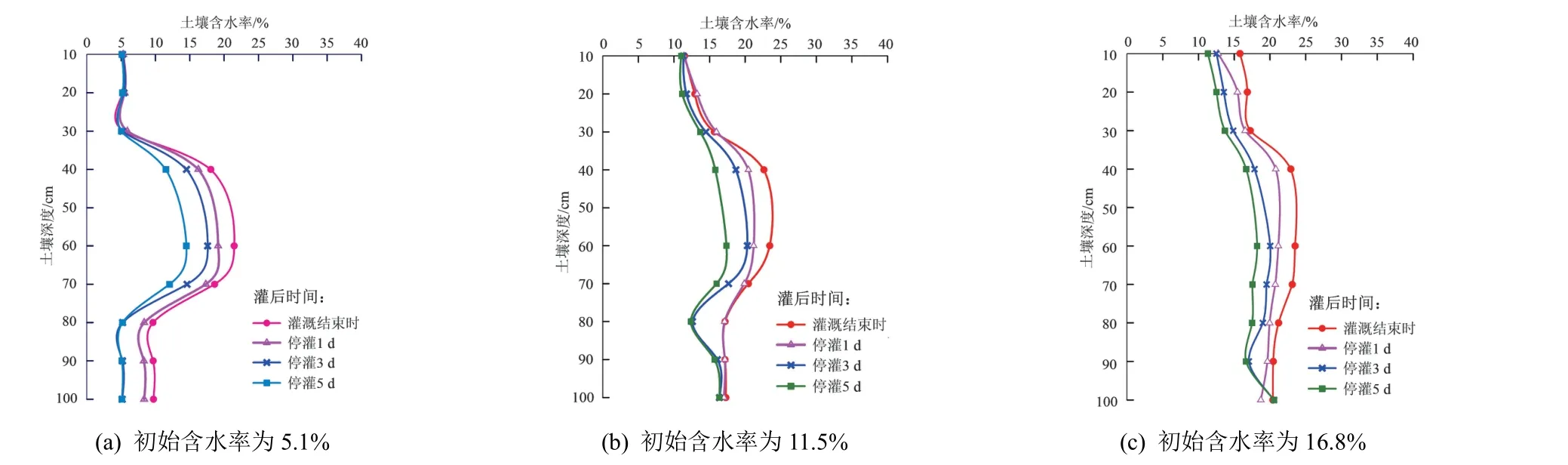
图6 初始含水率对湿润体垂直方向水分再分布的影响Fig.6 Effect of initial water content on vertical water redistribution of humidified bodies

灌溉结束时土壤水分主要集中分布在40～70 cm处（渗灌管中心位置附近），停灌1 d 后土壤含水率集中范围扩大为30～80 cm，停灌3 d 和停灌5 d 后土壤含水率明显下降，远低于田间持水率，但总体变化趋势与停灌1 d 相似。以土层深度30～80 cm 为研究对象，利用式（6）计算湿润土体均匀度CU，初始含水率为5.1%时，灌溉结束时、停灌1 d、停灌3 d 和停灌5 d 湿润体内水分分布均匀度CU分别为61.00%、62.59%、56.45%、62.35%；初始含水率为11.5%时，灌溉结束时、停灌1 d、停灌3 d 和停灌5 d 湿润体内水分分布均匀度CU分别为86.06%、89.88%、84.69%、89.27%；初始含水率为16.8%时，灌溉结束时、停灌1 d、停灌3 d 和停灌5 d 湿润体内水分分布均匀度CU分别为91.21%、93.54%、91.65%、92.77%。故停灌1 d 后湿润体内垂直方向含水率分布相对均匀，湿润体特征可作为田间指导灌水的主要依据。

2.4.2 对湿润体水平方向水分再分布的影响

图7 为初始含水率对湿润体水平方向水分再分布的影响。由图7 可知，随着水平距离的增加，土壤停灌时与停灌结束后的含水率均呈先减小后趋于稳定的趋势。不同初始含水率条件下，湿润体水平方向水分主要集中在距管0～25 cm 处，在初始含水率为5.1%的水平方向25～35 cm 处，再分布后的土壤含水率大于灌溉结束时，初始含水率为11.5%、16.8%处理的土壤含水率随着停灌时间的延长整体呈减小趋势。这主要是由于风沙土质地粗、孔径大，当土壤含水率低于土壤有效水阶段时，湿润锋仍将不断运动，促进了水分的水平运移。

图7 初始含水率对湿润体水平方向水分再分布的影响Fig.7 Effect of initial water content on water redistribution in the horizontal direction of wet body

以水平距管0～25 cm 为研究对象，用式（6）计算不同初始含水率条件下湿润体水平方向水分分布均匀度可得，初始含水率为5.1%时，灌溉结束时、停灌1 d、停灌3 d 和停灌5 d 湿润体内水分分布均匀度分别为62.85%、71.88%、69.32%、70.21%；初始含水率为11.5%时，灌溉结束时、停灌1 d、停灌3 d和停灌5 d 湿润体内水分分布均匀度分别为94.82%、96.48%、95.39%、94.94%；初始含水率为16.8%时，灌溉结束时、停灌1 d、停灌3 d 和停灌5 d 湿润体内水分分布均匀度分别为96.38%、97.31%、97.22%、95.96%。故湿润体内水平方向土壤含水率分布同样在停灌1 d 后相对均匀，湿润体特征可作为田间指导灌水的主要依据。

综上可知，停灌1 d 后湿润体内垂直方向和水平方向含水率分布相对均匀，为了进一步探究不同初始含水率对地下渗灌管埋深和间距的影响，对比此阶段含水率数值与土壤有效含水率（田间持水率的65%），可知，随着初始含水率的增大，渗灌管适宜埋深与间距也在增大。其中，风沙土在初始含水率为5.1%时，渗灌管适宜埋深应小于10 cm，管间距应小于30 cm；初始含水率为11.5%时，渗灌管适宜埋深应小于20 cm，管间距应小于60 cm；在初始含水率为16.8%时，渗灌管适宜埋深应小于30 cm，管间距应小于90 cm，以保障作物正常生长。

3 讨 论

本研究发现，风沙土地下渗灌下湿润体形状近似渗灌管为中心的椭圆形，初始含水率对湿润体形状的影响较大。这与张俊等[16]研究结果不同，这可能是由于地下渗灌与微润灌不同，地下渗灌属于管道式线源灌溉，管壁渗水孔较多，当初始含水率大于土壤入渗能力时，容易产生积水，使得重力势及渗灌管侧面与土壤作用力变大，湿润锋在不同方向的推进速率随初始含水率增大而增大，且向下运移速率大于向上和水平方向，因此形成左右截距相同、上下截距不同的椭圆体。本研究发现随着初始含水率的增大，地下渗灌累计入渗量和入渗速率变小。康金林等[17]研究不同初始含水率条件下对均质红壤水分入渗规律影响也得到相同结论，主要原因是其他条件一致时，初始含水率越高，入渗初期的土壤水吸力越弱，加上水分的持续输入，土壤含水率逐渐增大，土壤孔隙度减小，相同时间内的入渗率和累积入渗量也就越低。

本研究采用4 种入渗模型对风沙土入渗过程进行拟合，并表明Kostiakov 模型回归结果R2均值为0.783，对风沙土高初始含水率条件下的拟合效果较差。Philip 模型对均质土壤垂直入渗的适宜性较好[18-19]，而本试验采用Philip 模型进行拟合，发现对稳定入渗速率和高初始含水率条件下的拟合精度不够。曾辰等[8]认为Philip 入渗模型能够较好地描述不同初始含水率条件下砂黄土和塿土的入渗过程。而其试验结果与本研究不同的原因是二者灌溉装置与土壤质地不同，地下渗灌原理与其他种类灌水器差异较大。Horton 模型回归结果R2均值在4 个模型中最高，对不同初始含水率下风沙土水分入渗均有较好的适用性。通用经验模型中初始含水率与稳定入渗率成正比，与初始入渗率成反比，这与实测数据不一致。综合分析评价，Horton 模型更适用于拟合地下渗灌风沙土水分入渗特征。

根据灌水结束后湿润体水分分布情况表明土壤水分主要集中分布在垂直方向40～70 cm 范围，水平方向0～25 cm 范围，即土壤水分变化率范围集中在渗灌管位置附近，继而向四周逐步扩散，距离渗灌管出水孔位置越远，水势梯度增大，土壤含水率不断减小[20]。灌水均匀度是评价灌水质量的重要指标，也是灌溉系统设计的关键参数[21]。本研究发现在湿润体垂直方向和水平方向，不同处理均在停灌1 d 后含水率分布相对均匀，这与刘显等[22]研究结果一致，再分布1 d 后湿润体特征可作为田间指导灌水的主要依据。但再分布后水分主要集中分布在30～80 cm 处，需注意初始含水率过高造成水分深层渗漏和蒸发损失[23]。杨明达[24]通过HYDRUS-2D 模型模拟及田间试验表明，风沙土条件下滴灌带埋深30 cm，间距60 cm 是冬小麦-夏玉米的最佳布设参数。焦炳忠[25]研究认为，砂质土条件下地下渗灌灌水器埋深大于30 cm 后，会存在渗漏现象。本研究中不同初始含水率对地下渗灌管埋深和间距有较大的影响，通过对水分再分布后土壤含水率数值的分析可以得出，初始含水率为5.1%、11.5%、16.8%时，渗灌管适宜埋深应分别小于10、20、30 cm，管间距应分别小于30、60、90 cm。在实际应用中，地下渗灌管布设参数的选择还需要根据土壤质地、作物需水规律等实际情况综合考虑。

本文采用土箱模拟试验对不同初始含水率下风沙土入渗特性进行研究，阐明了风沙土入渗过程，但未对不同质地土壤及作物进行系统研究，后续还需要继续探讨影响地下渗灌土壤水分入渗的其他因素，为干旱半干旱地区地下渗灌技术的实际应用与推广提供理论依据。

4 结 论

1）地下渗灌下湿润体形状近似椭圆形，并随着初始含水率的增大，形状特征越明显。湿润锋在不同方向的推进速率与初始含水率正相关。

2）同一时刻下初始含水率越大，累计入渗量和入渗速率越小，累积入渗量和入渗时间符合幂函数关系，入渗系数与初始含水率负相关，入渗指数与初始含水率正相关。

3）与Kostiakov 模型、Philip 模型和通用经验模型相比，Horton 模型对不同初始含水率下风沙土入渗过程拟合效果较好。

4）不同初始含水率对风沙土地下渗灌管埋深和间距有较大的影响，初始含水率为5.1%、11.5%、16.8%时，渗灌管适宜埋深应分别小于10、20、30 cm，渗灌管间距应分别小于30、60、90 cm，即风沙土湿度越大，渗灌管埋深越深，渗灌管间距可相应增大。

（作者声明本文无实际或潜在的利益冲突）