塔柏刺形叶特征与叶面积估算模型*
王露露 张有福 陈一博 陈春艳 宋晨慧
(河南科技大学农学院 洛阳 471023)
叶片作为植物与周围环境接触面积最大的器官,其形态和大小的变化体现其对环境的适应性,因而对环境变化具有重要指示作用(Lavorelet al., 2010;Chaiet al., 2016;张林等,2004)。叶面积(leaf area,LA)的大小直接影响叶片对光的截获能力(Luoet al., 2004),常作为衡量植物光合能力的基础参数,并应用于评价植物碳同化能力和生态适应性等多方面(Wonget al.,2015;Mazziniet al., 2010)。因此,快速、准确地测定LA 对植物生理、形态及生态系统特征与功能的研究都有重要意义。
植物的叶形态存在差异,其LA 的测量方法也有较大的差异。常见的方格计数法、打孔法和叶面积仪测量法等均适用于阔叶型LA 测定;披针形的狭长叶片可采用游标卡尺法和手持叶面积仪测量;(彭曦等,2018)。针叶型LA 的测量可利用WinSEEDLE 种子和针叶图像分析系统(刁军等,2013 ;蔡琰琳等,2008)。然而,大多数测量LA 的方法都是破坏性的。在观察植物个体发育过程中,对植物生长和生理的动态变化进行研究时,通常需要连续测量LA(Saitoet al., 2020)。此外,在叶片被移除后一些生理指标可能会发生很大程度的变化,因此,破坏性测量叶片会导致生理试验的误差(Yuet al., 2020)。目前,常采用构建经验模型来无损测量植物的LA。大多采用叶形态学指标,如叶长、叶宽、叶长与叶宽的乘积与LA 之间的关系来构建经验模型(Azeemet al., 2020;Shiet al., 2019;Tayet al., 2020;Ribeiroet al., 2018;巫娟等,2020),可连续无损伤估算LA。
本研究以我国北方广泛分布,且在园林栽培和水土保持造林工程中常用的植物塔柏(Juniperus chinensiscv. Pyramidalis)为试验材料,采用游标卡尺对1 270 片塔柏刺形叶进行测量,测得叶长(leaf length,LL)、叶基宽(leaf base width,LBW)、最大叶宽(maximum leaf width,LWmax)以及叶厚(leaf thickness,LT)4 个形态学指标,使用Photoshop CS5 图像处理软件对叶片的图像进行处理并计算LA。采用多元线性模型和单变量线性函数y=ax+b、指数函数y=aebx和幂函数y=axb对形态学指标数据进行拟合,筛选出最优的LA 经验模型,为准确估算塔柏刺形叶LA 提供了简洁的方法,也为研究刺形叶性状指标之间的关系提供数据基础。
1 材料与方法
1.1 研究材料
塔柏是柏科(Cupressaceae)圆柏属圆柏(Juniperus chinensis)的栽培种,主要分布于中国华北及长江流域各地。叶多为刺形,绿色中脉两侧有条白2 粉带,叶片小而狭长,数量多,从叶基到叶顶部逐渐变尖,近披针形(图1),长度大约为6~12 mm,最大宽约为1.1 mm,厚度约为0.4 mm。

图1 塔柏刺形叶形态示意Fig. 1 Schematic diagram of the spiny leaves in J. chinensis
1.2 研究方法
1.2.1 样本采集与数据收集 2019 年4 月在河南科技大学(34°36′0″N,112°25′28″E)的70 株塔柏上随机采集无病、虫害的刺形叶,每株约19 片,共1 270 片。使用游标卡尺(精确到0.05 mm)测量塔柏刺形叶的LL(叶连接叶柄的最底端到叶尖端的距离)、LBW(叶连接叶柄的最底端的横向宽度)、LWmax(叶横向最大宽度)以及LT(叶长1/2 处厚度)。将叶片平铺在标准方格纸上(最小方格规格为1 mm2),在同一光照条件下,将数码相机(1 600 万像素)水平垂直固定在距离方格纸30 cm 处对叶片拍照并导入计算机。参照Wang 等 (2020)和李乐等(2016)的方法,在每张图片选取固定位置的小方格(1 mm2)为参照物,使用Photoshop CS5 软件进行图像处理得到每张图片上叶片与小方格(1 mm2)的像素个数,利用数字图像的成像原理,即总像素数除以单位面积(1 mm2)像素数,获得相应图形的面积(孟祥丽等,2019)。计算公式为:
式中:LA 为实测叶面积(mm2);N为测量叶片的像素数(个);P为小方格的像素数(个);S为小方格面积(mm2)。
1.2.2 经验模型的构建、检验与评估 在所有数据中随机选取80%的数据用于构建LA 的经验模型,剩余20%的数据用于评估经验模型的精度。为探究不同叶形态学指标对LA 的影响与贡献量,采用多变量线性模型并使用逐步法对经验模型进行优化。进一步探究单个形态学指标对LA的估算,根据散点图分布情况,分别采用线性函数y=ax+b、指数函数y=aebx和幂函数y=axb等3 类模型进行拟合,y为实测LA,x为叶片结构参数,a、b为经验模型的系数。用加权最小二乘法解出方程系数并进行计算得出LA 拟合面积模型,使用SPSS 等软件计算方程参数、制图表。在构建多变量线性模型时,利用方差膨胀因子(variance inflation factor,VIF)检验变量间是否存在多重共线性问题(Marquaridt, 1970):
式中:r是变量之间的相关系数,若VIF 值大于10,说明变量间存在明显的多重共线性,因此,构建模型时必须剔除其中1 个变量;若VIF 值小于10,表明二者的多重共线性问题可忽略,构建模型时2 个参数均可保留。
筛选最佳拟合估算模型综合参考决定系数(R2)、均方误差(root mean square error,RMSE)、赤池信息准则(Akaike information criterion,AIC)。选择R2最接近1、且RMSE 值最小的模型为最优经验模型,优先选择AIC 值最小的模型为最优经验模型,当选择最优的前2 个经验模型间AIC 的差值小于2 时,选择RMSE值较小的模型为最优经验模型(吴凤婵等, 2021)。
基于最优经验模型计算得到LA 的预测值,分析其残差的分布情况,当近似正态分布且大部分残差点落在残差平均值±3 倍标准差的范围内时,认为该经验模型可靠、合理(Chianget al., 2003)。为评估模型的可靠性,使用剩余的20%数据进行回归分析,基于最优经验模型,以LA 实测值为y,预测值为x,检验回归方程的拟合效果。根据回归线斜率与1 接近程度、截距的大小以及决定系数R2,来判定预测值和实际值的吻合程度,并计算最优经验模型的预测精度(FA)。各参数公式如下(王彦君等, 2018):
式中:K为经验模型中参数的个数;n 为样本数;yi为 第i个样本的LA 实测值;fi为第i个样本的LA 预测值;abs 表示绝对值函数。
1.2.3 数据分析 采用Microsoft Excel 2016 软件记录和整理数据,数据分析与模型拟合使用IBM SPSS Statistics 22.0 软件。
2 结果与分析
2.1 塔柏刺形叶形态学指标的特征
通过对塔柏刺形叶形态学指标进行分析(表1),结果表明,在1 270 片单叶样本中,塔柏刺形叶形态学指标变异系数大小:LA>LL> LWmax> LBW> LT,LA 的变异系数最大(CV=0.301),均值为(7.433±2.235)mm2(平均值±标准偏差, 下同),其数值分布在7.307~7.556 mm2(95%CI)。LL 和LWmax的变异系数分别为0.212、 0.206, LL 和LWmax均值分别为(9.004±1.907)mm、(1.014±0.209)mm,LL 和LWmax数值分布区间分别为8.898~9.110 mm(95%CI)、1.003~1.026 mm(95%CI)。LBW 的变异系数较小(CV=0.162),均值为(0.780±0.126)mm, 其数值分布在0.774~0.788 mm 9(5%CI)。LT 变异系数最小(CV=0.158),数值波动和偏差最小, 数值分布与均值最接近(SE=0.002,MAD=0.050),均值为(0.385±0.061) mm,数值分布在0.382~0.388 mm(95%CI)。
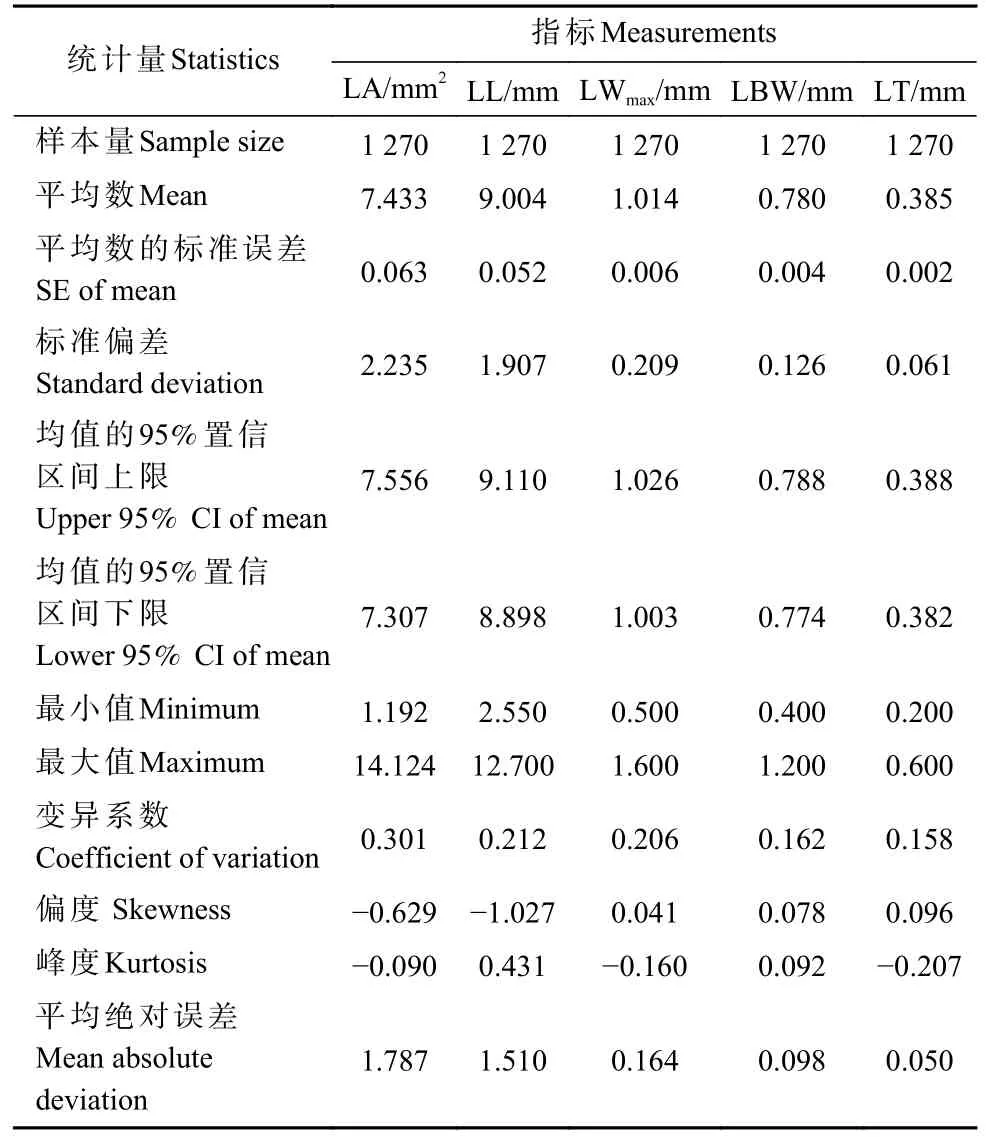
表1 塔柏刺形叶形态指标值总体分布特征①Tab. 1 Overall distribution characteristics of leaf morphological index for spiny leaves of J. chinensis
2.2 塔柏刺形叶形态学指标相关性
通过对塔柏刺形叶形态学指标相关性分析(表2)可知,LA 与LL 和LWmax都显著相关,且相关系数最高,分别为0.858、0.794,LBW 与LA 的相关系数最低(r=0.341)。
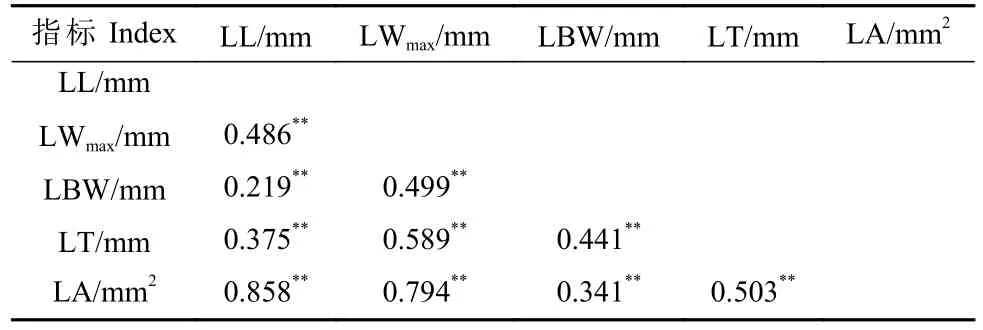
表2 塔柏刺形叶形态学指标的相关性①Tab. 2 Correlation of morphological indexes in the spiny leaves of J. chinensis
2.3 塔柏刺形单叶面积多元回归模型
利用公式(2)计算并分析4 个形态学指标LL、LWmax、LBW、LT 之间的多重共线性问题,经计算LL、LWmax、LBW、LT 之间的VIF 值均小于10,说明LL、LWmax、LBW、LT 之间的多重共线性问题可忽略,其在构建模型时可同时存在。
将4 个形态学指标LL、LWmax、LBW、LT 与LA进行多变量线性拟合和优化。首先,选择全入法来构建多变量线性回归方程模型1(表3):Y=-3.755+0.720X1+5.780X2-1.136X3-1.104X4(R2=0.914,RMSE=0.666,AIC=2 059.602),式中:X1表示LL,X2表示LWmax,X3表示LBW,X4表示LT。虽然模型1 的拟合度很好(R2=0.914),但是模型1 中LT 这一指标的回归系数并不显著(P=0.069)。所以,使用逐步法对其进行优化。在模型2 中,LL 为自变量,模型2 的方程为:Y=-1.686+1.003X1(R2=0.725, RMSE=1.191, AIC=3 238.133)。在模型2 的基础上引入变量LWmax,得到模型3:Y=-4.497+0.725X1+5.331X2(R2=0.911,RMSE=0.678,AIC=2 492.517),式中:X1为LL,X2为LWmax。继续引入变量LBW,得到模型4:Y=-3.879+0.718X1+5.679X2-1.177X3(R2=0.914, RMSE=0.667, AIC=2 060.969),其中X1、X2、X3分别为LL、LWmax、LBW。此时除了LT 由于回归系数不显著被排除(P=0.069),模型4 以最少的变量达到了最大的拟合度(R2=0.914,RMSE=0.667,AIC=2 060.969)模型4 被认为最优多变量回归模型。
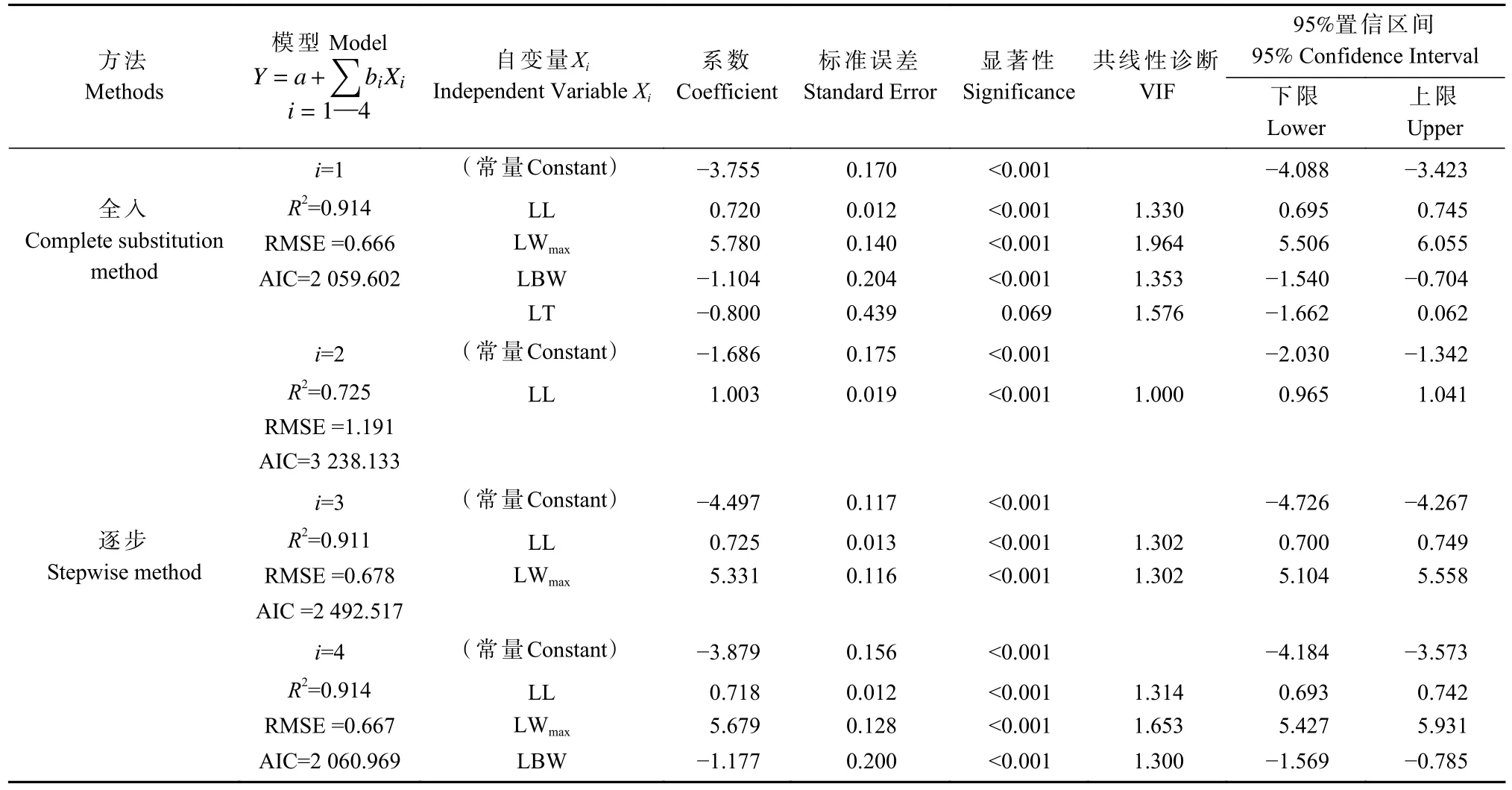
表3 塔柏刺形叶形态学指标多变量线性回归Tab. 3 Multivariate linear regression of leaves morphological indexes in J. chinensis
2.4 塔柏刺形叶面积单变量回归模型
为探究单变量对LA 估算的影响,根据各个形态学指标散点图的分布,分别采用线性函数y=ax+b、指数函数y=aebx和幂函数y=axb等3 类模型进行拟合。拟合结果表明(表4),4 个塔柏刺形叶形态学指标与LA 都有极强的显著性(P<0.001),各拟合模型的R2、RMSE 和AIC 值分别介于0.077~0.805、0.174~2.183、3 238.133~5 033.099。在3 种拟合模型中,与LA 拟合优度最好的均是基于LL 的模型:Y=-1.686+1.003X(R2=0.725,RMSE=1.191,AIC=3 238.133);Y=1.3660.180X(R2=0.776,RMSE=0.187,AIC=3 401.459);Y=0.356X1.367(R2=0.850,RMSE=0.174,AIC=3 261.810),其中LA 的最优单经验模型为基于LL 的线性单变量模型。
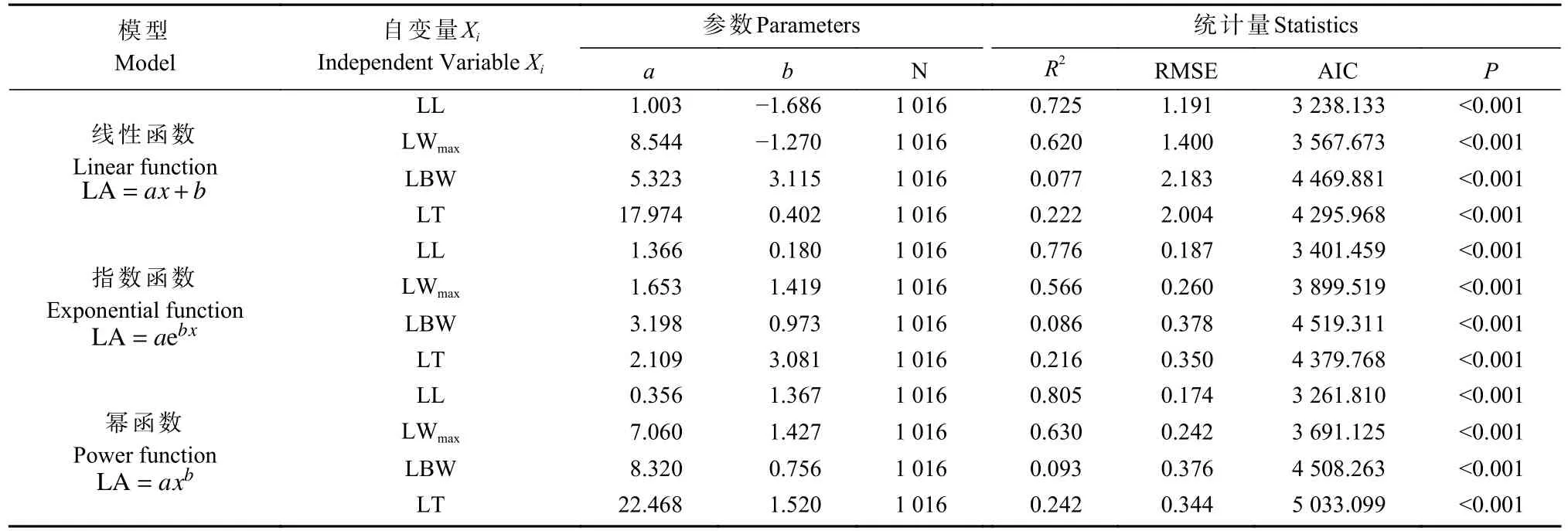
表4 塔柏刺形叶叶面积单变量回归模型①Tab. 4 Leaf area index model of the spiny leaves in J. chinensis
2.5 最优叶面积估算模型检验与评估
筛选出的2 个模型拟合的LA 估算值的残差图呈正态分布(图2),均有99%的残差点分布在残差平均值±3 倍标准差的范围内,初步证明本研究所构建的最优LA 经验模型预测叶面积的可靠性。
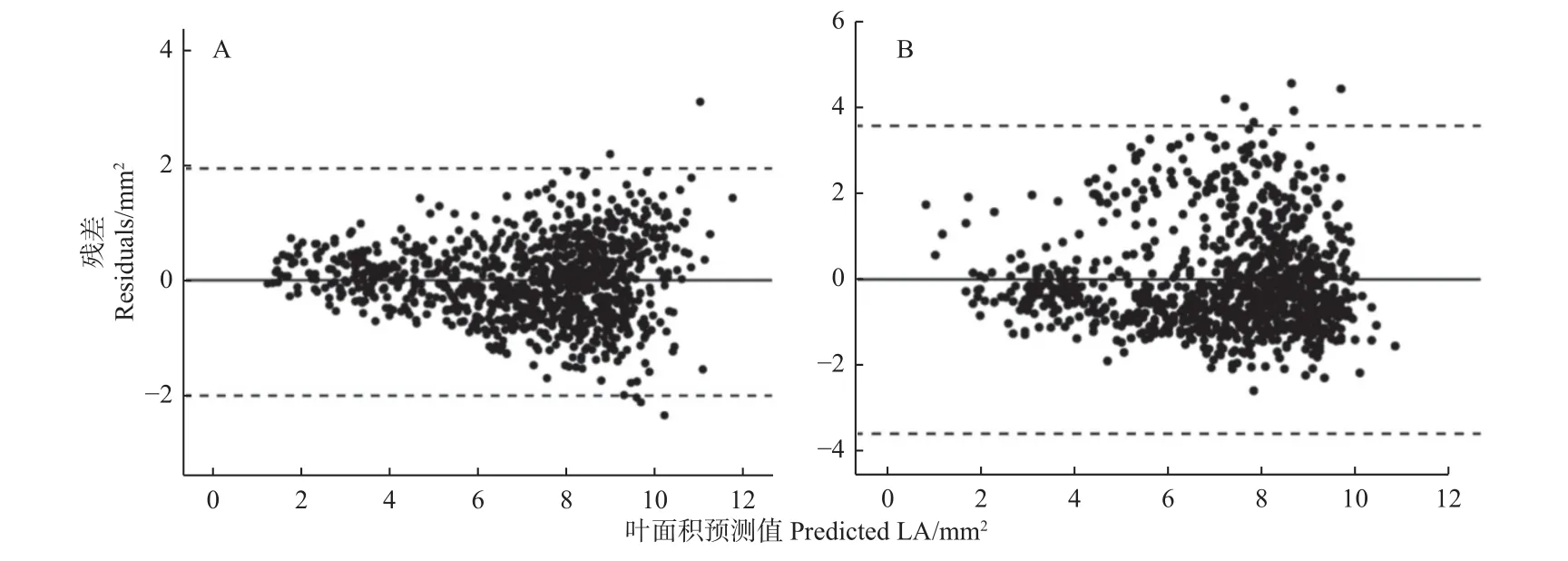
图2 LA 的残差分布Fig. 2 Residuals plot of LA
为进一步评估这些最优经验模型的可靠性,使用剩余20%的数据基于筛选出的最优模型计算塔柏刺形叶LA 的预测值,以LA 实测值为x,预测值为y,检验回归方程的拟合效果如图3 所示,图中虚线为y=x直线方程,2 种模型的LA 预测值与实测值的回归分析方程基本趋近于该直线方程,多元线性模型与基于LL 的单变量线性模型LA 预测值与实测值的回归分析方程的决定系数R2分别为0.953、0.747,表明多元线性模型拟合度更优。使用剩余20%的数据,由公式(6)计算可得,最优多元线性模型4 与基于LL 的单变量线性模型对LA 的预测精度分别为96.21%、91.16%,表明2 个模型均能准确预测塔柏刺形叶LA,但多元线性模型精确度更高。
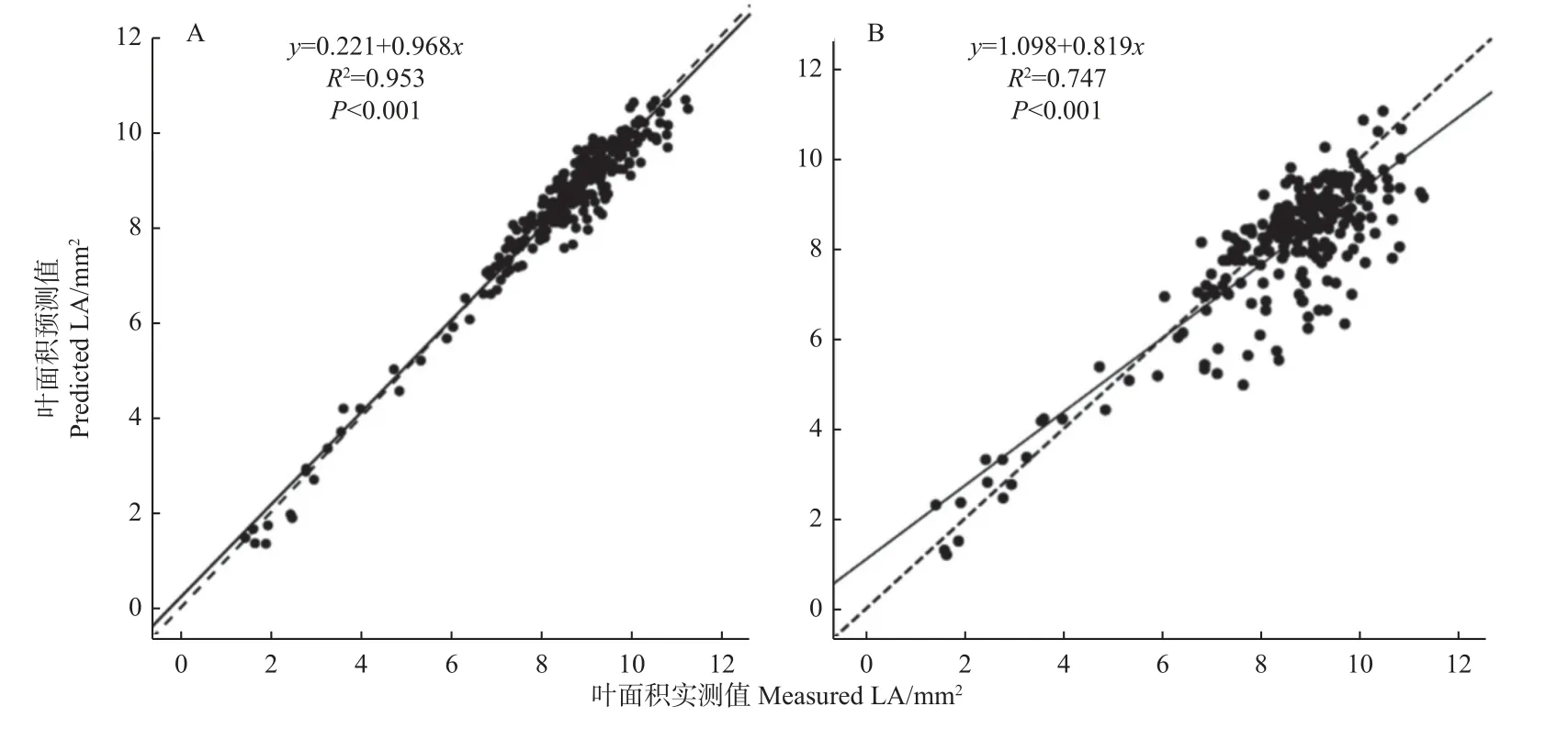
图3 LA 预测值与实测值的回归分析Fig. 3 Regression analysis of LA between predicted and measured value
3 讨论
3.1 塔柏刺形叶特征
在测定的5 个形态学指标中,塔柏刺形叶LA 的变异系数是最大(CV=0.301),说明塔柏刺形叶LA 有较大的可塑性。塔柏刺形叶属于微小的披针形叶片,叶尖呈针状。LL 的变异度比LWmax更大(CV=0.212,0.206)。塔柏刺形叶形态学指标的相关性分析表明,LL 与LA 呈显著正相关(r=0.858)(表2),由此可推测,塔柏刺形叶LA 的变异度主要归因于叶性状本身(如LL)变异度。这一结果与已有的杉木的披针形叶片的研究结果相似,即LL 比LWmax对于LA 大小的影响更为显著(彭曦等,2018)。本研究中刺形叶LA 的95%CI 范围在7.307~7.556 mm2,LA 有效值范围精确,但标准偏差偏大(SD=2.235),推测造成标准偏差偏大的主要原因是由于本研究随机采样涵盖了不同叶龄、树龄、冠层以及阴阳面叶片,叶片大小存在较大的差异。本研究中LL、LBW、LWmax、LT 数值的集中分布体现塔柏刺形叶形态学指标测量精确度高;LL 和LA均有较大的变异系数,且二者相关分析达到显著水平,这些对模型建立的可靠性提供依据。
3.2 塔柏刺形叶面积估算模型
通过进行多变量线性回归拟合发现LL、LWmax对LA 的影响最大。在对LA 估算模型的研究中,LL和LW 常作为直接指标来对LA 进行估算(Leiteet al.,2019; Dalmagoet al., 2019; Oliveiraet al., 2019;Bakhshandehet al., 2011)。本研究得到的LA 最优多变量回归模型的预测精度为96.21%,精确度高,但是建立多变量线性模型需要引入多个变量,计算较为复杂。为了得到更简便的LA 预估模型,分别采用线性函数y=ax+b、指数函数y=aebx和幂函数y=axb等3 类模型进行拟合,得到最优单变量模型为基于LL 的线性模型:Y=-1.686+1.003X(R2=0.725, RMSE=1.191,AIC=3 238.133),预测精度为91.16%。多变量线性模型的预测精度更高,其值达96.21%。因此,从精确度判断,建议采用多变量线性模型对于塔柏刺形叶LA进行估算。这与前人研究不同,如针叶的叶面积模型,多采用LL 作为最佳指标(谢龙飞等,2018;刁军等,2013;解雅麟等,2019),阔叶叶面积多选择LW 作为最优指标(Santanaet al., 2018;Toebeet al., 2019;Ribeiroet al., 2019)。由于披针形叶LW 对LA 的影响比针叶型大,比阔叶型小。因此,估算LA 既要考虑LL,也要考虑LW 的影响。
4 结论
塔柏刺形叶LA 均值为7.433±2.23 mm2,数值分布7.307~7.556 mm2(95%CI);通过对LA 与LL、LWmax、LBW、LT 进行相关分析和模型拟合,得到最优的多变量线性模型为:Y=-3.879+0.718X1+5.679X2-1.177X3(R2=0.914,RMSE =0.667,AIC=2 060.969),其中X1、X2、X3分别为LL、LWmax、LBW。最优的单变量模型为:Y=-1.686+1.003X(R2=0.725,RMSE=1.191,AIC=3 238.133)。2 种模型的预测精度分别为96.21%、91.16%,表明2个模型均能准确估算塔柏刺形叶LA,但多元线性模型精确度更高。因此,应用刺形叶叶面积模型可有效、准确地无损测量塔柏刺形叶面积,有利于刺形叶相关性状连续性测量,这为微小叶形植物单叶面积和生产力估算和相似叶形的叶性状模型的构建提供借鉴。

