测试木材剪切模量的自由方板扭转模态法
王 正 谷晓雨 周宇昊 张一凡 沈肇雨 黄俣劼
(南京林业大学材料科学与工程学院 南京 210037)
在土木建筑、家具和木材加工行业中,锯材是木结构建筑、高档家具制造、室内装修门窗制造、木地板等产品的必备主材,对其力学性能的检测和质量评等尤为重要(Wanget al.,2014;Yoshiharaet al.,2009;Zhouet al.,2007)。木材弹性模量动态测试在全球开展得很活跃,技术较成熟,研究成果也较多。剪切模量是木材的重要弹性常数,因木材为正交各向异性材料,木材剪切模量动态测试(Wanget al.,2016;王正等,2017;Wanget al.,2019a;Wanget al.,2018)具有一定难度,在国内外尚不太成熟,深入开展木材剪切模量动态测试很有必要。目前,在自由状态下测试木材剪切模量的动态方法主要有自由板扭转振型法(Wanget al.,2019a;程可等,2015)、自由杆件扭转振动法(JIS A1127—2001)、Timoshenko-Hearmon 梁迭代法和自由方板扭转振动法(Nakaoet al.,1987)。然而这些方法在动态测试木材剪切模量的根据、适用性和测试精度上存在一定不足,即自由板扭转振型法仅能满足木材自由板试件长宽比l/b≥3 的条件要求,受板长宽比要求限制;自由杆件扭转振动法从测试精度考虑也存在对试件长宽比的限制;Timoshenko-Hearmon 梁迭代法因受试件尺寸限制要求,甚至迭代发散;自由方板扭转振动法因其推算剪切模量公式采用一个与材料类型和方板宽厚比无关的固定系数 0.9,必然会产生一定误差,从测试精度考虑,特别不适用于测试木材剪切模量。
静态测试木材或木基结构板材剪切模量的方法有 ASTM D3044—16 标准法、NPL 法、MNPL 法和Lee’s 法(Yoshiharaet al.,2006;Yoshihara,2009),其共同特点是用足够薄的方板试件,通过测试施力点挠度推算板材剪切模量,其中ASTM D3044—16 标准法规定的方板宽厚比为 25~40,NPL 法和Lee’s 法认为方板宽厚比应不小于35。本研究提出一种基于自由方板扭转模态动态测试木材剪切模量的新方法——自由方板扭转模态法。首先,根据木材自由方板特有的一阶扭转振型特征和能量法,导出木材主向剪切模量与其自由方板一阶扭转频率之间的关系式;然后,基于自由方板在不同树种和不同宽厚比时ANSYS 计算的一阶扭转模态频率,进行仿真和回归分析,获得木材主向剪切模量与其自由方板一阶扭转频率之间的修正关系式(自由方板扭转模态法关系式);同时,其测试木材剪切模量的有效性采用自由杆件扭转振动法(动态)和非对称四点弯曲法(静态)进行试验验证。本研究最大创新点在于即使降低方板试件的宽厚比要求,仍能保证剪切模量测试精度,研究结果可为建筑工程、家具、室内装饰、交通、军事、乐器等行业的工程应用提供可靠支撑。
1 方法
1.1 木材自由方板一阶扭转振型特征
设方板长为l、宽为b、厚为h(l=b),用刚性系数<1.0 N·cm-1的弹性绳悬挂。取板中心为坐标原点O,x轴沿方板轴线,自顺木纹纹理方向或木质复合板纵向,其正向水平向右;z轴铅直向下为正;y轴沿方板宽度,其正向按右手螺旋规则确定,如图1 所示。
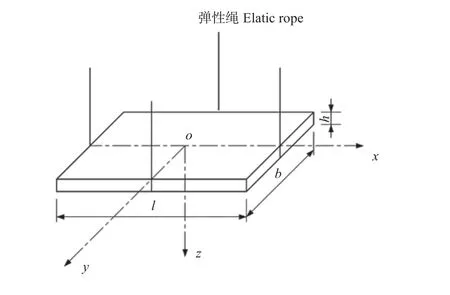
图1 方板自由悬挂及其坐标系Fig. 1 Square plate free suspension and its coordinate system
采用ANSYS 19 Solid185 单元模态程序块计算山毛榉(Fagus longipetiolata)弦向自由板(长宽比l/b=1和3)的一阶扭转振型,网格划分沿x和y向40 等分,沿z向 6 等分,即40×40×6 网格划分。ANSYS 模态程序块计算时,输入山毛榉弦向材料常数(尹思慈,1996)。模态计算设置为最大长度归一,从模态计算输出信息中读取一阶扭转频率和一阶扭转振型z向位移(无单位)。
根据山毛榉自由方板(长宽比l/b=1)的一阶扭转振型,读取x=l/2、y=b/2板边界上各节点的z向位移,绘制沿板长边和宽边的扭转振型曲线(图2)。山毛榉自由方板(l=b)的一阶扭转振型特征为:在板长边y=b/2上各点,z向位移W(x,b/2)沿x(x/l)轴方向变化近似于一条直线,在板宽边x=l/2上各点,z向位移W(l/2,y)沿y(y/b)轴方向呈曲线变化,该曲线可用无常数项的y四次多项式拟合。
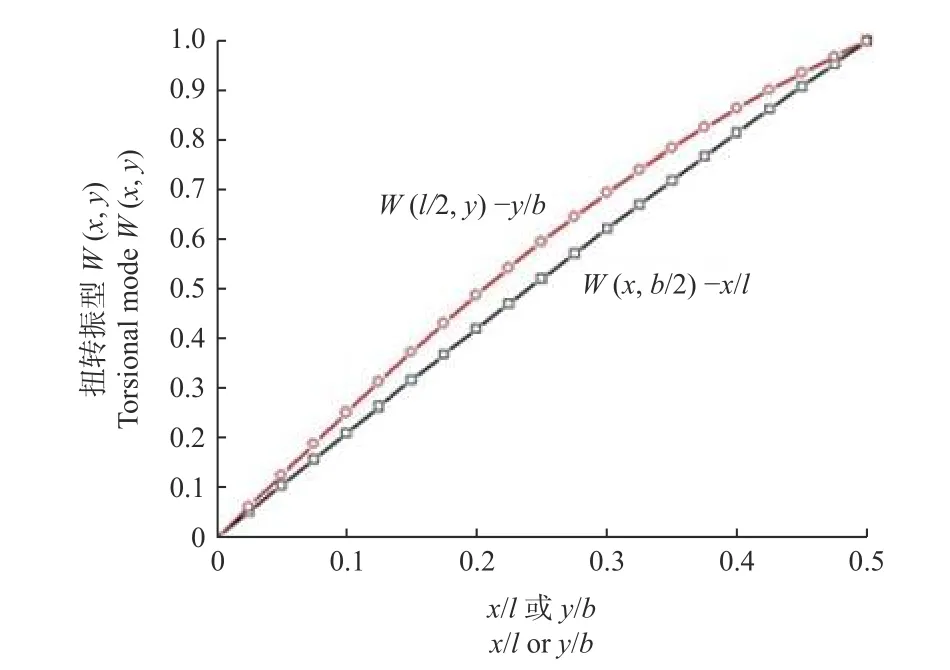
图2 山毛榉自由方板(l/b=1)在其边界y=b/2 或 x=l/2 上沿x 或y 向的扭转振型Fig. 2 Torsional vibration mode of Fagus longipetiolata free square plate (l/b=1) along x-direction or y-directiony-direction on its boundary y=b/2 or x=l/2
对于长宽比不小于3 的自由方板,如图3 中l/b=3的山毛榉自由板,经ANSYS 计算,一阶扭转振型特征不同于自由方板:在板长边y=b/2上各点,z向位移W(x,b/2)沿x(x/l)轴方向呈曲线变化,该曲线可用无常数项的x四次多项式拟合;在板边界x=l/2上各点,z向位移W(l/2,y)沿y(y/b)轴方向变化近似于一条直线。
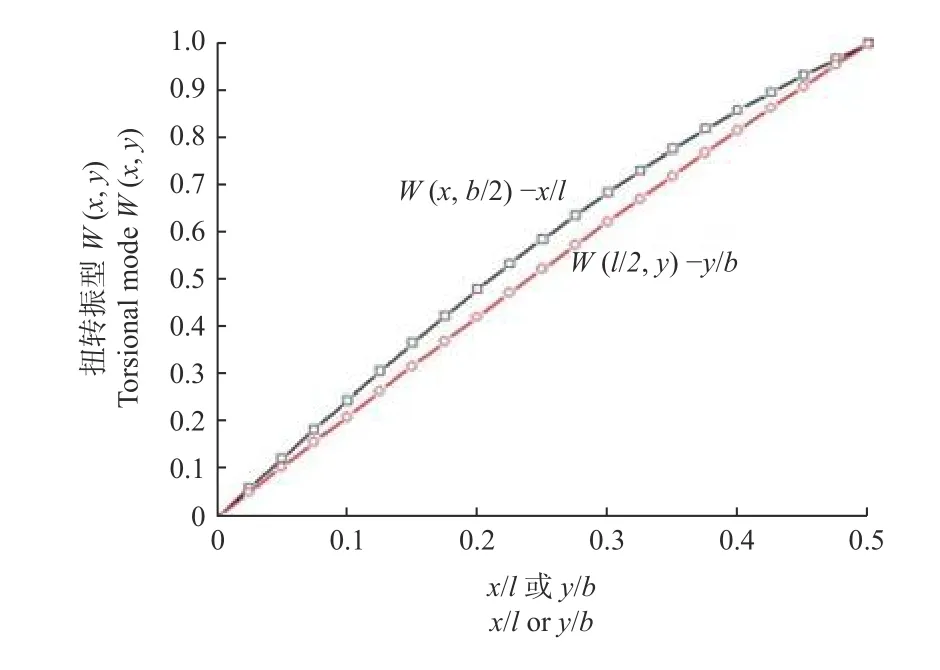
图3 山毛榉自由板(l/b=3)在其边界y=b/2 或 x=l/2 上沿x 或y向的扭转振型Fig. 3 Torsional mode mode of Fagus longipetiolata free square plate (l/b=3) along x-direction or y-directiony-direction on its boundary y=b/2 or x=l/2

图4 LT、LR、RT 主向面方板(l=b)的主向L、T、R 与x、y、z 对应示意Fig. 4 Corresponding relationship between L, T, R and x, y, z in LT, LR, RT main face plate (l=b)
经ANSYS 计算,对于西加云杉(Picea sitchensis)、欧洲赤松(Pinus sylvestris)和北美黄杉(Pseudotsuga menziesii)等自由方板的一阶扭转振型特征,即沿板长边扭转振型z向位移直线变化,沿板宽边扭转振型z向位移曲线变化均与山毛榉自由方板相同。
对于l=2b的自由方板,其一阶扭转振型沿板长边和宽边的变化规律既不同于l=b的自由方板,也不同于l/b≥3 的自由方板,而是沿板长边和宽边呈重合曲线变化,因此木材自由方板一阶扭转振型特征按其长宽比可分为3 种:l/b=1、l/b=2 和l/b≥3 的自由方板。采用自由方板为试件测试木材剪切模量时,需从自由方板特有的一阶扭转振型特征出发,建立其一阶扭转振型函数。本研究建立的自由方板(l=b)一阶扭转振型函数,与Wang 等(2019a)自由方板长宽比l/b不小于3 的一阶扭转振型函数截然不同(图2、3),尽管其均应用能量法和优化原理。
1.2 木材剪切模量与其自由方板一阶扭转频率的关系式
设自由方板(l=b)的一阶扭转振动为:
式中:W(x,y)为自由方板一阶扭转振动的振型函数;ω为自由方板一阶扭转固有圆频率。
根据自由方板一阶扭转振型W(x,y)在方板y=b/2 边界上(沿x向)呈直线变化、在x=l/2 边界上(沿y向)呈曲线变化的特征(图2)以及一阶扭转振型节线位置(x=0,y=0),可将其设为:
式中:k由x=l/2、y=b/2的z向位移等于W(l/2,b/2)确定;系数A、B、C、D满足的方程组通过如下目标函数L取最小值确定:
自由方板绕y轴的转角为:
因自由方板一阶扭转振型相对于板中间截面(y=0)为反对称,故计算其动能和应变能可按1/2 方板(0≤y≤b/2, -l/2 ≤x≤l/2)进行。
式中: ρ为材料密度;ft为自由方板一阶扭转频率,Hz。
应变能U:
则
或写成
式中:G为剪切模量,Pa;l为方板沿木纹纹理方向的长度,m;b为方板垂直于木纹纹理方向的长度,m;h为方板厚度,m; ρ为气干密度,kg·m-3;ft为方板一阶扭转频率,Hz; γ为木材自由方板振型系数,其值取决于与方板动能(IT)和应变能(Iϕ)相关的2 个定积分计算值;为方板矩形截面因子。
1.3 木材自由方板振型系数计算
根据振型系数 γ的定义,基于木材主向材料常数的数值特征,选择西加云杉、山毛榉、欧洲赤松和北美黄杉等树种的自由方板,先应用ANSYS 19 Solid185 单元模态程序块对方板进行40×40×6 网格划分,计算其一阶扭转振型,后将在板宽边x=l/2 上的扭转振型分量Wi代入由优化原理决定的A、B、C、D的线性方程组中,求解方程组确定系数A、B、C、D,进而计算IT、Iφ积分值。
ANSYS 19 Solid 185 单元模态程序块输入参数如表1 所示。
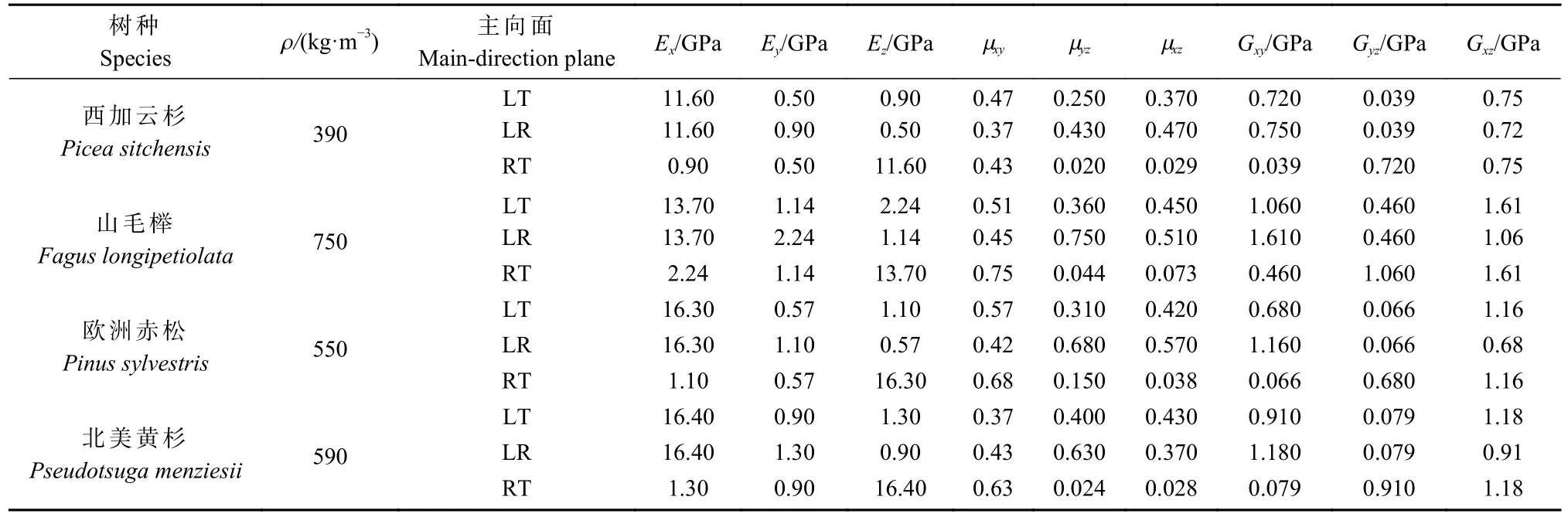
表1 西加云杉、山毛榉、欧洲赤松和北美黄杉等树种ANSYS 模态程序块计算的输入参数(尹思慈,1996)①Tab. 1 Input parameters of ANSYS modal block calculation of Picea sitchensis, Fagus longipetiolata, Pinus sylvestris and Pseudotsuga menziesii
计算振型系数时,取云杉、山毛榉、欧洲赤松和北美黄杉 4 种树种,每树种 3 个主向面(LT、LR、RT),自由方板宽厚比取 7、10、15、20、25 和30 共6 种,总计72 种计算方案。
对自由方板在1 种宽厚比下计算的 12 个振型系数,按主向将4 种树种振型系数取平均值作为该主向在该宽厚比下的木材振型系数,该宽厚比下的振型系数个数按主向为3,6 种宽厚比的振型系数为 18 个,如表2 所示。
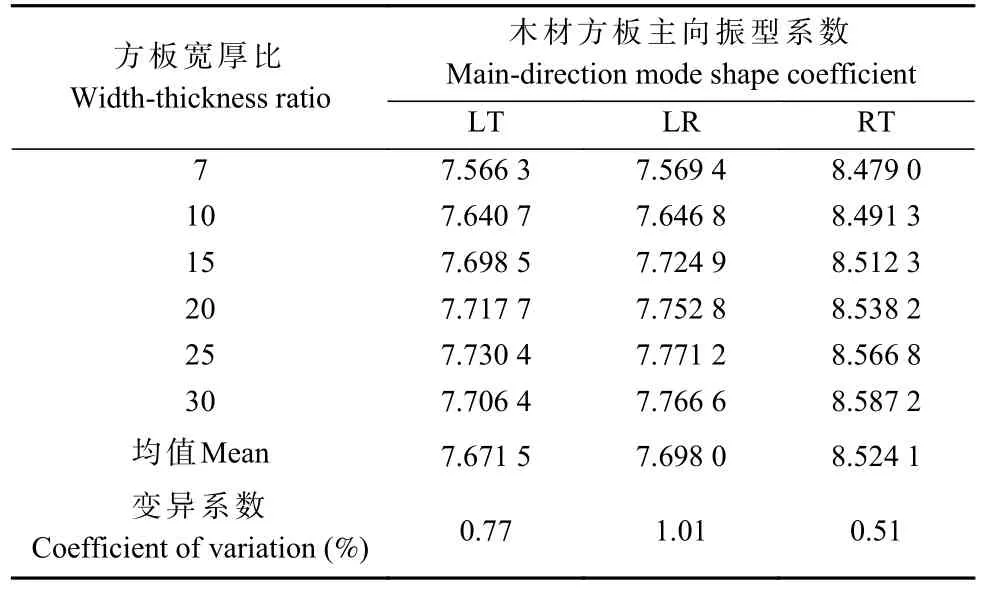
表2 自由方板在不同宽厚比时计算的木材主向振型系数Tab. 2 Main-direction mode shape coefficient of timber free square plate at the different width-thickness ratio
由表2 可知,木材弦向自由方板振型系数均值为7.671 5,变异系数为0.77%;木材径向自由方板振型系数均值为7.698 0,变异系数为1.01%;木材横向自由方板振型系数均值为8.524 1,变异系数为0.51%。
根据式(1),木材弦向剪切模量与其自由方板一阶扭转频率的关系式为:
木材径向剪切模量与其自由方板一阶扭转频率的关系式为:
木材横向剪切模量与其自由方板一阶扭转频率的关系式为:
式中:GLT、GLR和GRT分别为木材弦向、径向和横向剪切模量;ft为自由方板一阶扭转模态频率。
虽然ANSYS 模态程序块输出自由方板一阶扭转振型z向位移的同时还输出其一阶扭转模态频率,但在推导式(1)和与式(2)~(4)相关的振型系数计算中并未用到模态频率。从完备性考虑,还需验证将输出的一阶扭转模态频率计算值代入式(2)~(4)中计算的G(称为剪切模量仿真值)是否等于相应的主向剪切模量输入值,即主向剪切模量参考值。
1.4 式(2)~(4)的适用范围及其修正
验证剪切模量仿真值Gs是否等于相应的主向剪切模量参考值Gr,应从试验和仿真2 方面进行。用于仿真验证的树种,除上述云杉、山毛榉、欧洲赤松和北美黄杉4 种树种外,还增加白腊木(Fraxinus chinensis)、桃花心木(Swietenia mahagoni)和轻木(Ochroma lagopus)3 种树种。对7 种树种应用ANSYS 19 Solid 185 单元进行40×40×6 网格划分,计算长 140 mm、宽 140 mm,宽厚比 7、10、15、20、25 和30 的自由方板一阶扭转模态频率;将其代入式(2)、(3)、(4)中,得到各自主向剪切模量仿真值Gs。同时计算出宽厚比7、10、15、20、25 和30 各树种主向Gs与Gr比值,取各树种Gs/Gr均值作为木材主向在该宽厚比下的Gs/Gr。木材主向Gs/Gr随方板厚宽比的变化规律如图5所示。
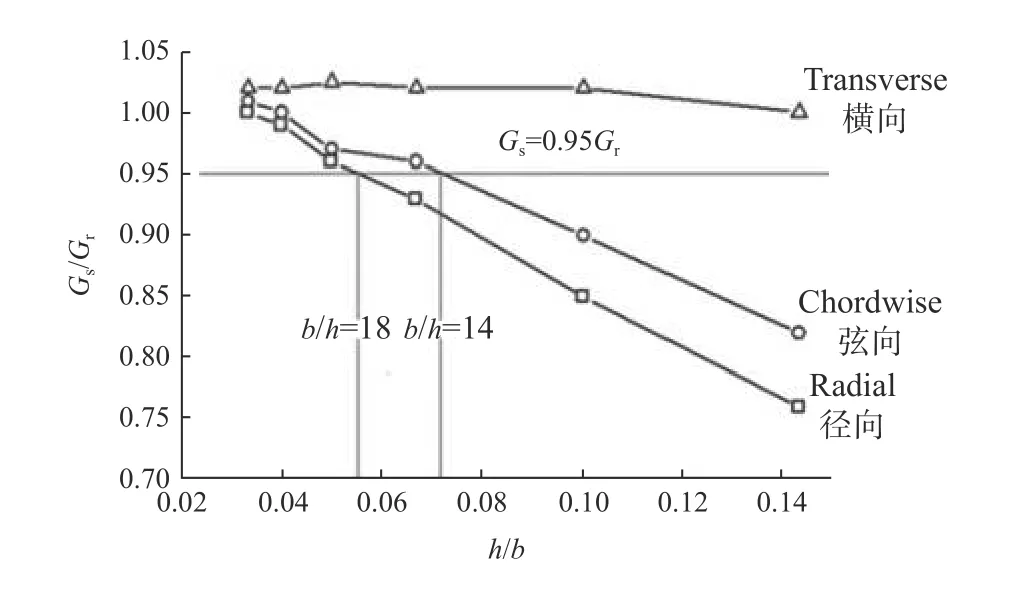
图5 木材Gs/Gr 随方板厚宽比的变化规律Fig. 5 Variation of the Gs/Gr value of wood with the thickness-towidth ratio of the square plate
由图5 可知,Gs随方板宽厚比的变化规律为:1) 对于木材弦向和径向,Gs随方板宽厚比增加而上升,逼近于Gr,且弦向和径向Gs与其参考值Gr的相对误差小于5%的方板宽厚比,分别可取17 和20;2) 对于木材横(切)向,Gs随其方板宽厚比变化平稳,且宽厚比在7~30 范围内,横(切)向Gs与其参考值Gr的相对误差均小于5%(约2%)。
对于Gs与Gr的相对误差不超过5%而言,本研究明确:式(2)适用于宽厚比不小于17 的自由方板测试木材弦向剪切模量;式(3)适用于宽厚比不小于20的自由方板测试木材径向剪切模量;式(4)适用于宽厚比 7~30 的自由方板测试木材横向剪切模量。因此,为保证式(2)、(3)测试木材剪切模量精度,要求木材弦向和径向的自由方板宽厚比分别不小于 17 和 20作为试件,然而这对于木材方板试件而言太苛刻。为了放宽这一要求,需对式(2)、(3)进行修正。
将Gs/Gr对方板厚宽比h/b进行回归分析,可得到相应的木材弦向因子kLT、径向因子kLR和横(切)向因子kRT依赖于方板厚宽比h/b的表达式。
木材主向剪切模量与其自由方板一阶扭转频率的关系式可修正为:
弦向
径向
横(切)向
式(5)、(6)和(7)适用于宽厚比7~30 的自由方板测试木材主向剪切模量,将其称为式(2)、(3)和(4)的修正关系式(即测试木材剪切模量的自由方板扭转模态法关系式)。由自由方板宽厚比适用范围为7~30的修正关系式仿真计算可知,其正确性还需从试验方面加以验证。
2 试验
2.1 材质与试件
树种:红雪松(Thuja plicata),弦向;铁杉(Tsuga chinensis),弦向;落叶松(Larix gmelinii),弦向和径向;西加云杉(Picea sitchenrsis),径向和横向;胶合板(plywood);定向刨花板(OSB)。
试件:方板试件、非对称四点弯曲试件和杆件试件,其参数和数量如表3、4 所示。
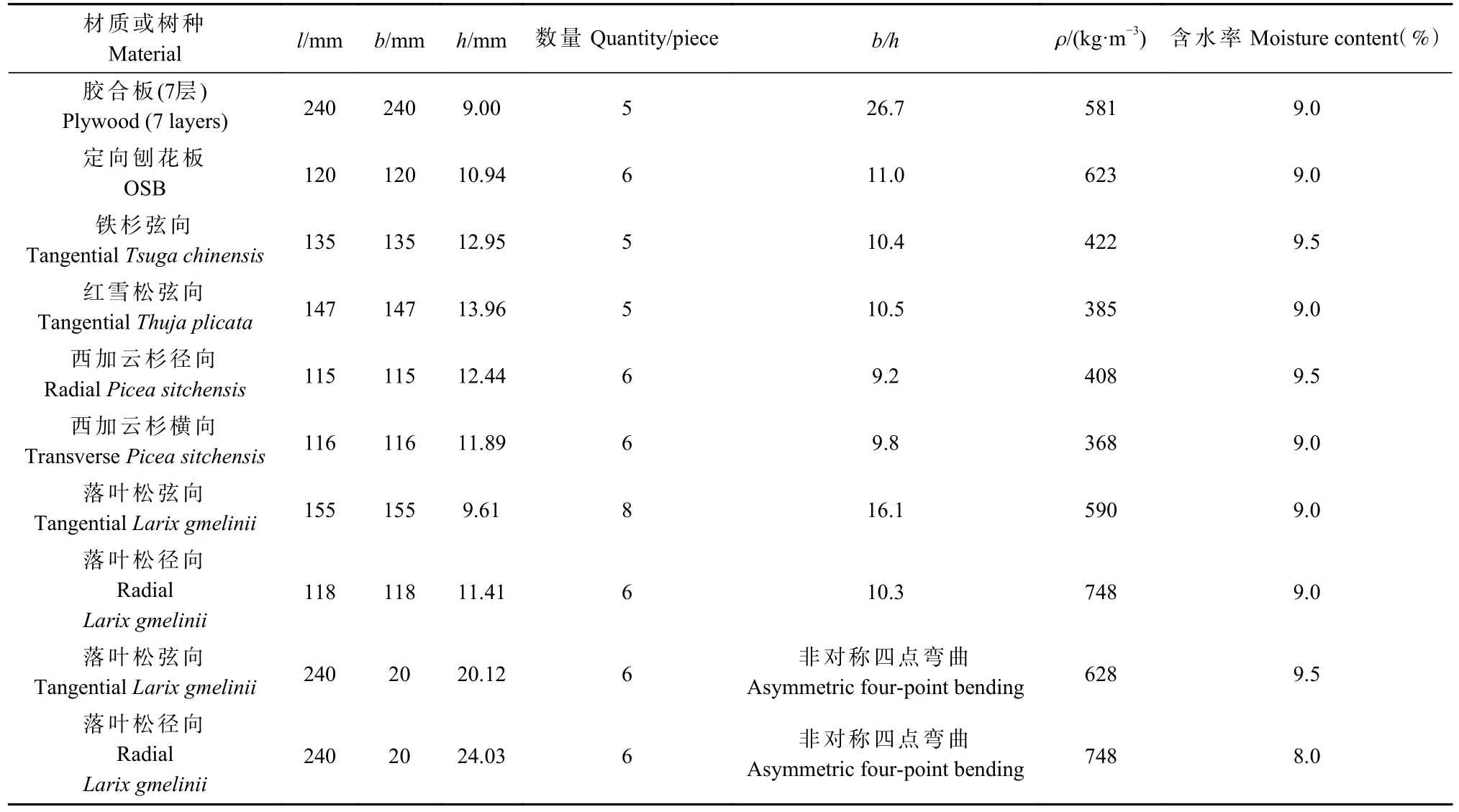
表3 方板试件和非对称四点弯曲试件基本参数Tab. 3 Basic parameters of square plate specimens and asymmetric four-point bending specimens
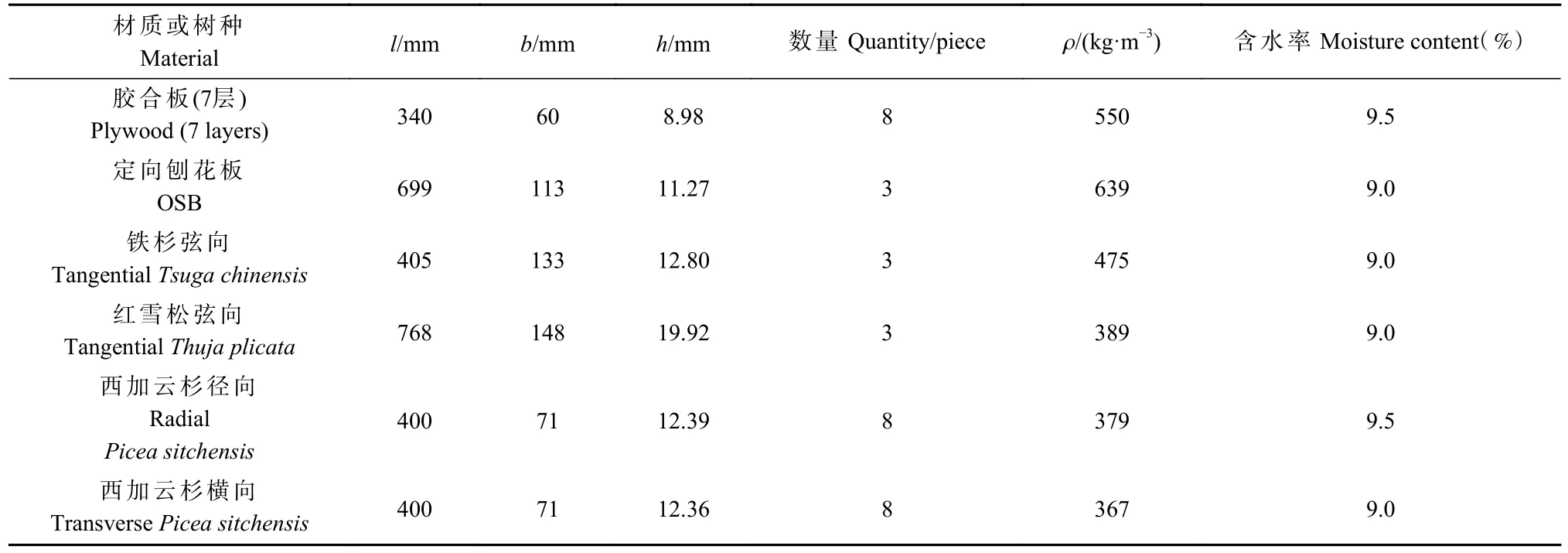
表4 自由杆件扭转振动法试件的基本参数(用于验证性试验)Tab. 4 Basic parameters of free-rod torsional vibration method (verification test)
2.2 试验设计
选择铁杉(弦向)、红雪松(弦向)、落叶松(弦向和径向)、西加云杉(径向和横向)制作方板试件,其宽厚比为9.2~16.1;选择胶合板(7 层)和OSB 木质复合板材制作方板试件,其宽厚比分别为26.7 和11.0(表3)。相应地制作适用于自由杆件扭转振动法和非对称四点弯曲梁法测试木材主向剪切模量的试件(表3、4)。用弹性绳以十字方式悬挂试件,实现其自由方板。对每种材质的自由方板试件,先测试其频谱,从频谱上读出自由方板一阶扭转频率;再采用自由方板扭转模态法关系式推算剪切模量。
对落叶弦向和径向试件,在其主向面中心处粘贴±45°方向应变片,采用全桥接法测试其主向面中心处剪应变,应用静态非对称四点弯曲梁法测试其剪切模量(Yoshiharaet al.,2006),以检验自由方板扭转模态法测试剪切模量的有效性;对铁杉弦向、红雪松弦向、西加云杉径向和横向试件,应用自由杆件扭转振动法测试其剪切模量(动态),以检验自由方板扭转模态法测试剪切模量的有效性。
2.3 试验仪器与设备
南京安正软件公司动态信号采集与分析系统1 套,包含信号调理仪、采集箱、计算机、谱分析和模态分析软件;KD6005 型八通道动态电阻应变计1 台;四点弯曲加载试验台 1 套;BX120-5AA 型电阻应变片(灵敏系数2.08);CA-YD-125 型压电式加速度计,声级计;其他仪器及其配套件:HK-30 木材含水率测试仪1 只、TG328B 电光分析天平(0.001 g)1 台、游标卡尺(0~150 mm)1 把、尼龙头小锤 1 把,0.425 、0.85、1.275、2.55 kg 规格砝码各3 只。
2.4 自由方板一阶扭转频率识别
从自由方板频谱图上正确识别出一阶扭转频率是准确测试木材剪切模量的关键。对于木材自由方板,通常在频谱图上出现的前二阶频率是一阶横向弯曲频率或一阶扭转频率,这就存在如何从2 个频率中正确识别出自由方板一阶扭转频率的问题。
真正识别自由方板一阶扭转频率需作模态试验。图6 所示为铁杉135 mm×135 mm×13 mm 自由方板模态试验的横向第一阶弯曲振型和第一阶扭转振型。由图可知,频谱第一高峰对应的频率为铁杉自由方板的横向一阶弯曲频率,第二高峰对应的频率为铁杉自由方板的一阶扭转频率。由于频谱上出现的前2 个高峰对木材自由方板而言必定是横向一阶弯曲频率和一阶扭转频率,故可根据自由方板横向一阶弯曲振型和一阶扭转振型的节线位置特征提出一种简易识别方法,即敲击自由方板中心,高峰下跌频率即横向一阶扭转频率,另一频率即横向一阶弯曲频率。自由方板横向一阶弯曲频率和一阶扭转频率在频谱上出现的前后顺序与木材主向面和方板宽厚比有关,如云杉弦向自由方板,当其宽厚比为10 时,先横向一阶弯曲,后一阶扭转,其径向自由方板,先一阶扭转,后横向一阶弯曲;当云杉自由方板宽厚比为7 时,弦向和径向自由方板频谱皆为前一高峰对应扭转频率,后一高峰对应横向弯曲频率。无论是哪种情况,可用上述简易识别方法从自由方板频谱前2 个高峰频率中识别出横向一阶弯曲频率和一阶扭转频率。
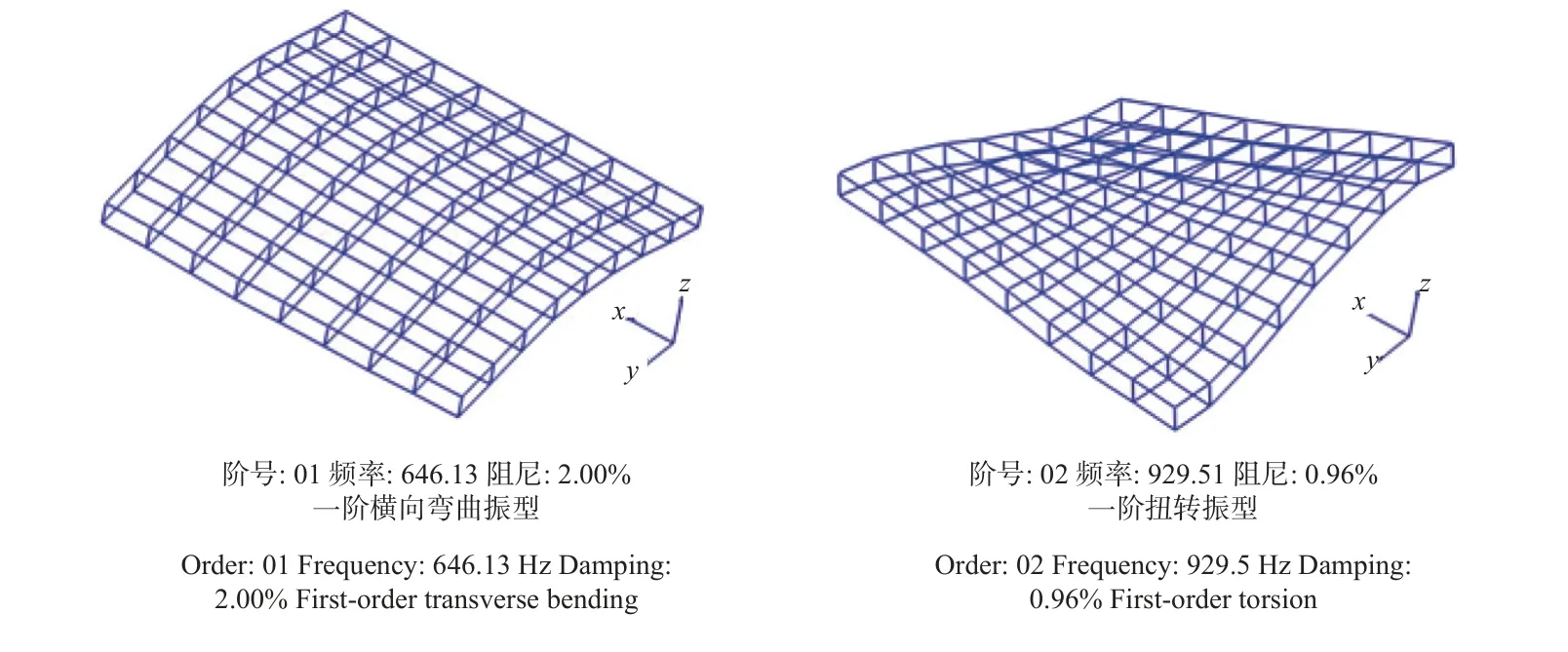
图6 铁杉135 mm×135 mm×13 mm 自由方板模态试验的横向一阶弯曲和一阶扭转振型(x 轴取顺木纹方向)Fig. 6 The transverse first-order bending and first-order torsional mode shapes of Tsuga chinensis 135 mm×135 mm×13 mm free square plate modal test (x-axis is taken along the direction of wood grain)
从图6 自由方板模态试验的一阶扭转振型可知,其板边y=b/2 的z向位移沿x方向呈直线变化,x=l/2的z向位移沿y方向呈曲线变化,与图2 计算模态的一阶扭转振型变化规律一致。
2.5 木材自由方板一阶扭转频率测试
为得到自由方板较为精确的一阶扭转频率测试值,自身质量小、测试传感器选用及其安装位置尤为重要,本研究推荐声级计或质量不大于1.5 g 的加速度计作为测试自由方板频谱传感器。根据试验摸索,自由方板一阶扭转频率的传感器最佳位置为:若使用声级计,将声级头置于下板面长边下方x=l/8 处,且距下板面 2~3 cm,敲击点位于方板宽边y=b/8 处;若使用加速度计,将其安装于上板面长边x=l/8 处,敲击点位于方板宽边y = b/8 处(图7)。如此测试的自由方板一阶扭转频率推算出的剪切模量与其他试验方法测试值相当吻合。
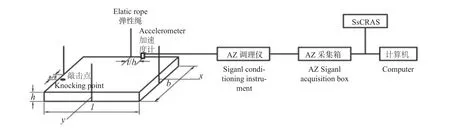
图7 测试自由方板(l=b)频谱Fig. 7 Test block diagram for testing the frequency spectrum of a free square plate (l=b)
红雪松自由方板测试频谱如图8 所示。应用上述简易识别方法,可从频谱图上识别出红雪松弦向自由方板的一阶横向弯曲频率和一阶扭转频率。
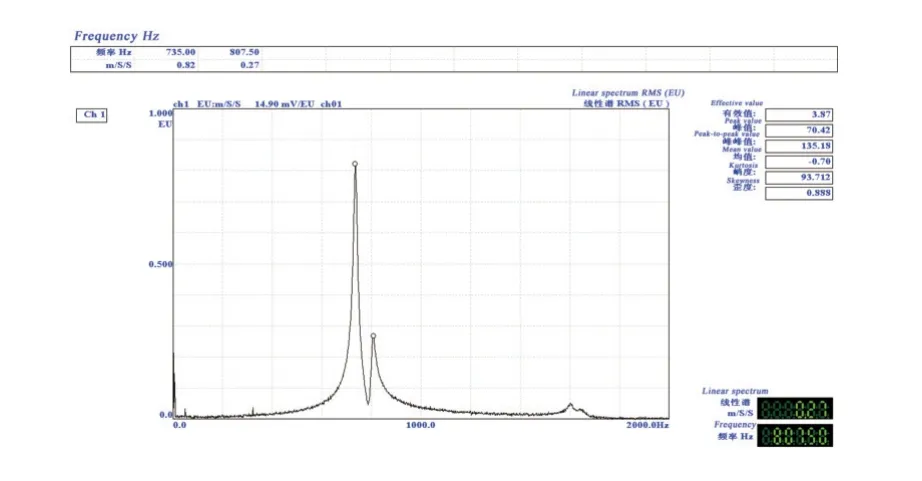
图8 红雪松2 号自由方板(147 mm×147 mm×13.96 mm)频谱Fig. 8 Thuja plicata No.2 free square board (147 mm×147 mm×13.96 mm) spectrum
3 结果与分析
3.1 自由方板扭转模态法测试木材剪切模量及其有效性的试验验证
自由方板扭转模态法测试木材弦向、径向和横向剪切模量源自于木材自由方板特有的一阶扭转振型特征、能量法原理和一阶扭转模态频率测试值,该方法除具有可靠的理论基础外,还考虑方板宽厚比和材质类别对剪切模量测试值的影响。
为验证自由方板扭转模态法测试木材剪切模量的有效性,采用自由杆件扭转振动法、非对称四点弯曲法进行试验验证。首先,验证弦向kLT因子和径向kLR因子的有效性,采用155 mm×155 mm×9.60 mm 落叶松弦向自由方板,测试其一阶扭转频率后,采用式(2)、(5)计算剪切模量测试值;然后,依次锯切边长为115、90 和70 mm 的方板,实现其不同宽厚比,并测试其一阶扭转频率;最后采用式(2)、(5)计算剪切模量测试值(表5,括号中百分数为变异系数)。
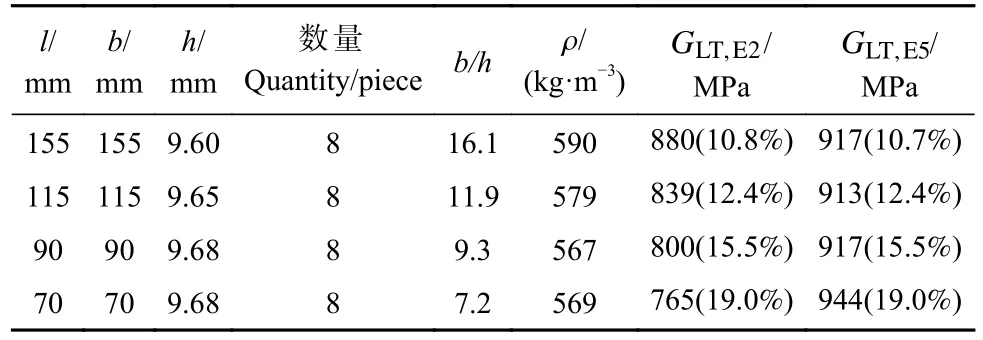
表5 落叶松弦向 155、115、 90 和70 mm 自由方板扭转模态法测试的剪切模量Tab. 5 Shear modulus of Larix gmelinii chordwise 155, 115, 90 and 70 mm free square plate torsional modal method
由表5 可知,落叶松弦向方板宽厚比从7.2 变至16.1 时,应用仅根据自由方板特有一阶扭转振型导出的式(2)测试的弦向剪切模量值从765 MPa 上升为880 MPa,变化幅度为115 MPa(占880 MPa 的13%);而应用自由方板扭转模态法式(5),当方板宽厚比从9.3 变至16.1 时,弦向剪切模量基本上为 917 MPa,仅在宽厚比为7.2 时,弦向剪切模量测试值才比917 MPa大27 MPa(占917 MPa 的2.9%)。因此,可以说自由方板扭转模态法(式5)用于测试木材弦向剪切模量,采用宽厚比不小于7 的方板具有足够精度。
由表6 可知,落叶松径向方板宽厚比为10.3 和14.8 时,应用仅根据自由方板特有一阶扭转振型导出的式(3)测试的径向剪切模量分别为1 232 和1 317 MPa,变化幅度为 85 MPa(占1 317 MPa 的6.5%);而应用自由方板扭转模态法式(6)测试的径向剪切模量分别为1 444 和1 426 MPa,变化幅度仅为18 MPa(仅占1 426 MPa 的1.3%)。因此,可以说自由方板扭转模态法用于测试木材径向剪切模量具有足够精度。

表6 落叶松径向 118 mm×118 mm 自由方板在宽厚比10.3 和14.8 时测试的剪切模量Tab. 6 Shear modulus of radial Larix gmelinii 118 mm×118 mm free square plate at width-thickness ratios of 10.3 and 14.8
此外,本研究还采用非对称四点弯曲法(静态)测试落叶松方板弦向和径向剪切模量,结果分别为910 MPa(11.6%)和 1 321 MPa(7.6%),与自由方板扭转模态法测试结果的相对误差分别为0.77%和7.9%。因此,自由方板扭转模态法用于测试木材弦向和径向剪切模量的有效性得到非对称四点弯曲法的试验验证。
自由方板扭转模态法(本研究)、自由杆件扭转振动法测试的铁杉弦向、红雪松弦向、西加云杉径向、西加云杉横向等主向剪切模量测试结果如表7 所示,表7 列出测试数据为应用自由方板扭转模态法式(5)、(6)、(7)所得。
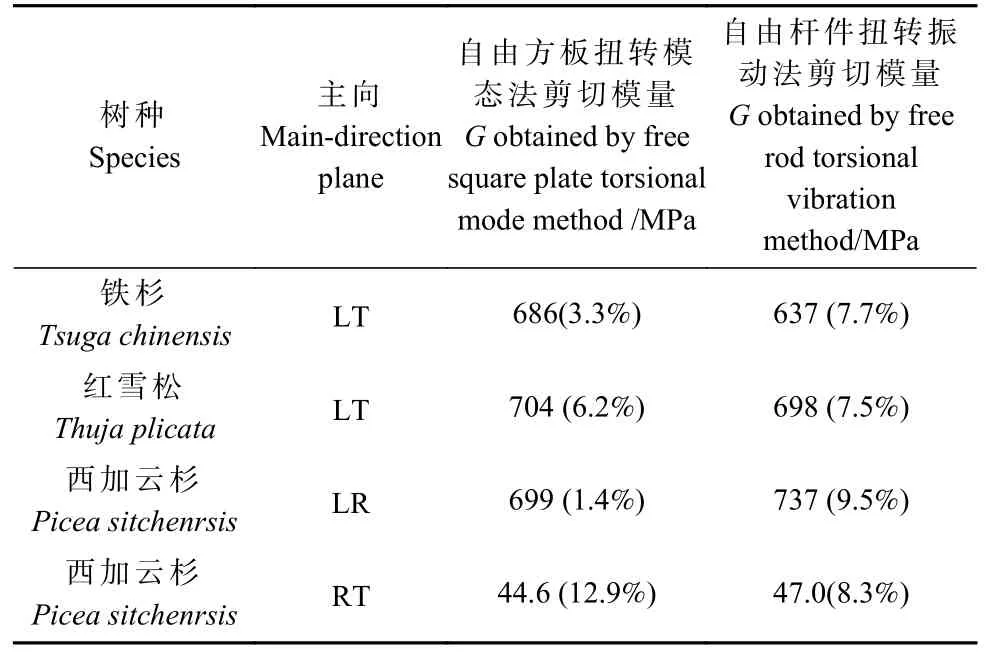
表7 自由方板扭转模态法测试木材主向剪切模量及其试验验证Tab. 7 Principal shear modulus of wood measured by free square plate torsional modal method and its experimental verification
由表7 可知,采用自由方板扭转模态法测试铁杉、红雪松和西加云杉剪切模量,相较于自由杆件扭转振动法测试剪切模量的相对误差在-5.2%~7.7%范围内,自由方板扭转模态法测试木材剪切模量的有效性得到自由杆件扭转振动法的试验验证。
3.2 自由方板扭转模态法用于测试木质复合材料剪切模量的可行性分析
对于各向同性材料,程可等(2015)给出测试剪切模量的振型系数为:
该振型系数依赖于自由板长宽比,适用于长宽比1~8 的自由板。
需要指出的是,程可等(2015)给出的振型系数适用于方板(l/b=1)的有效性未进行试验检验。为此,本研究用 80 mm×80.2 mm×3.45 mm、密度 7 771 kg·m-3和200 mm×199.8 mm×4.48 mm、密度 7 771 kg·m-3的低碳钢自由方板(各3 块),根据式(8)给出的振型系数测试剪切模量,其结果分别为 81.3 GPa(2.6%)和79.3 GPa(1.3%)。剪切模量测试值皆落在低碳钢剪切模量规范值79.2~82 GPa 范围内,因此式(8)给出的自由方板振型系数8.118 9 用于测试低碳钢剪切模量的有效性得到检验。
若将各向同性材料自由板的一阶扭转频率与剪切模量关系式用于l/b=1 的自由方板,可得:
现将式(9)用于OSB 测试剪切模量的依据说明如下:根据OSB 纵向和横向自由板在长宽比为1.25、1.5、2、3、4、5、6、8 计算的振型系数拟合式(Wanget al.,2019b),将其外推到板长宽比为1 的振型系数,可分别得到OSB 纵向和横向自由方板的振型系数分别为8.167 9 和8.058 6,之间相差1.4%,同时考虑这2 个振型系数与各向同性自由方板振型系数(γ=8.118 9)只差±0.7%,故可认为式(9)也适用于OSB自由方板测试其剪切模量。
考虑到方板宽厚比对测试木质复合材剪切模量的影响,取低碳钢方板长 140 mm、宽 140 mm,宽厚比7、10、15、20、25 和 30,采用ANSYS 计算其一阶扭转频率。ANSYS 计算输入的低碳钢方板材料常数为弹性模量206 GPa、泊松比0.3,密度7 850 kg·m-3。将ANSYS 输出的一阶扭转模态频率代入式(10)得到 6种宽厚比下低碳钢剪切模量仿真值。该仿真值除以低碳钢剪切模量参考值(取79.2 GPa)对方板厚宽比进行回归,得到对式(10)的修正因子kS。式(9)的修正公式可表示为:
将式(10)用于测试OSB 和胶合板剪切模量,其测试值与自由杆件扭转振动法测试的剪切模量相对误差分别为-0.1%和9.2%,如表8 所示。
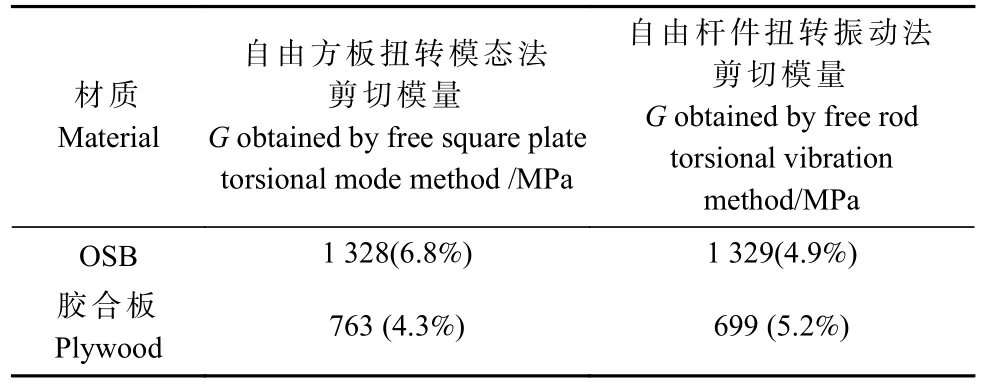
表8 OSB、胶合板剪切模量测试值Tab. 8 OSB, plywood shear modulus test values
自由方板扭转模态法用于测试OSB 和胶合板剪切模量的有效性得到验证。
需特别说明的是,式(10)用于测试木质复合板材剪切模量要作具体分析。就木质复合板材OSB 和MDF来说,根据前期测试结果,OSB 纵向弹性模量与横向弹性模量之比为 2.63,而MDF 横向弹性模量略大于纵向,纵向弹性模量与横向弹性模量之比约0.96,即式(10)用于测试OSB 和MDF 剪切模量是可行的,但这并不意味着对其他木质复合板材均适用,如LVL 纵向弹性模量与横向弹性模量之比为21.3,其量级同于木材的EL/ET或EL/ER。因此,考虑到LVL 板材制造由木材旋切胶粘压制成型,测试其剪切模量时,采用的不是式(10),而是木材弦向的式(5),测试结果表明是正确的。
3.3 自由方板扭转模态法和自由方板扭转振动法测试剪切模量结果对比
自由方板扭转振动法推算各向同性材料和木质胶合板剪切模量的公式(Nakaoet al.,1987)为:
式中:G为剪切模量,Pa;a为方板长,m;b为方板宽,m;h为方板厚,m; ρ为密度,kg·m-3;ft为方板一阶扭转频率,Hz。其中,方板长a对应于式(5)、(6)、(7)中的方板长l。
自由方板扭转模态法和自由方板扭转振动法测试木材和木质复合材料的剪切模量如表9 所示。
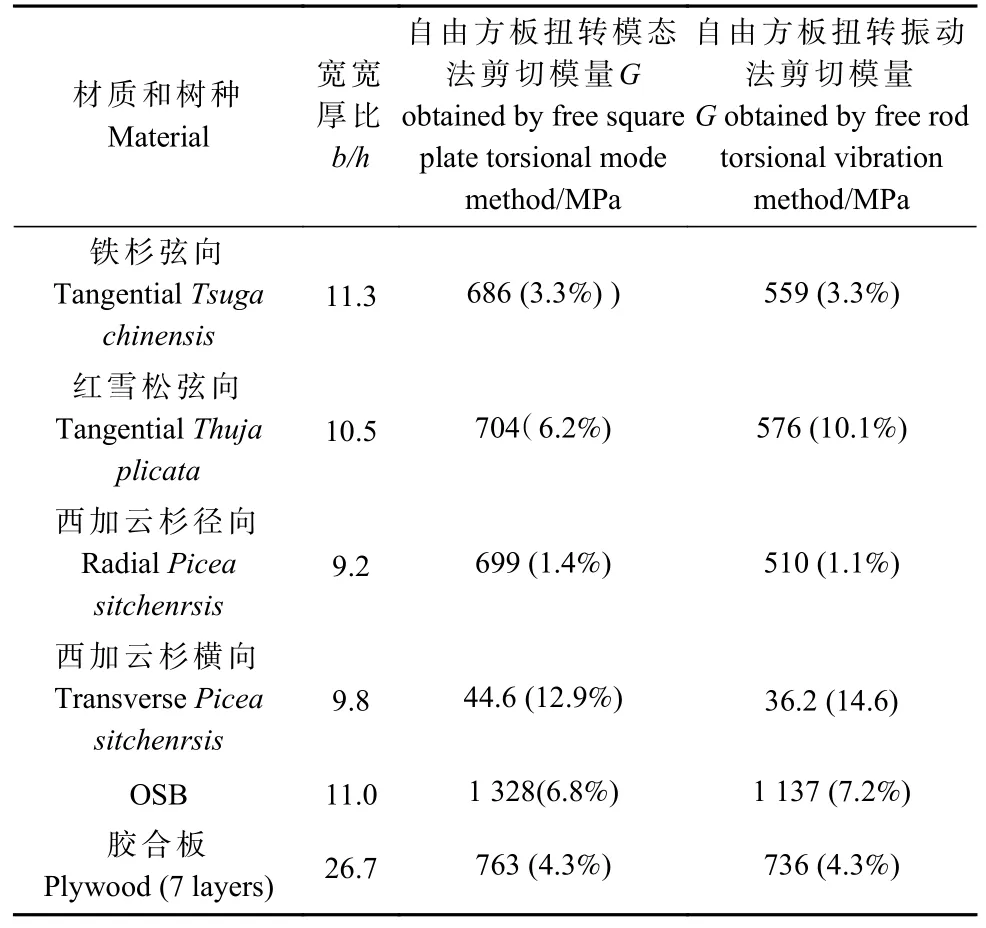
表9 自由方板扭转模态法和自由方板扭转振动法测试木材和木质复合材的剪切模量Tab. 9 Free-square-plate torsional modal method and freesquare-plate torsional vibration method for the determination of shear modulus of wood and wood composites
由表9 可知,自由方板扭转振动法测试木材和木质复合材料的剪切模量皆小于自由方板扭转模态法,其程度与试件宽厚比和材质有关,对于所测4 种树种木材3 个主向剪切模量测试值小22.2%~37.1%,对于所测胶合板和OSB 剪切模量分别小3.7%和16.8%。分析其原因,自由方板扭转振动法测试剪切模量时未计入方板宽厚比的影响,也未考虑材料类别,其公式采用统一系数0.9,故从测试精度考虑,自由方板扭转振动法不适宜测试木材主向剪切模量。
4 讨论
如前文所述,自由状态下测试剪切模量的动态方法主要有自由板扭转振型法、自由杆件扭转振动法、Timoshenko-Hearmon 梁迭代法和自由方板扭转振动法,并对各方法适用的限定条件作了阐述,如自由板扭转振型法仅能满足木材自由板试件长宽比l/b≥3的条件要求;自由杆件扭转振动法从测试精度考虑,也存在对试件长宽比的限制要求;Timoshenko-Hearmon梁迭代法受限于梁尺寸,出现迭代发散,计算不出剪切模量值等问题。
为定量说明上述方法限定条件对剪切模量的影响以及本研究的贡献,选用LVL 整板沿其纵向下料制作320 mm×100 mm×10.8 mm、 220 mm×100 mm×10.8 mm、100 mm×100 mm×10.8 mm 各3 块方板,采用自由板扭转振型法和自由杆件扭转振动法测试其纵向剪切模量,结果如表10 所示。

表10 自由板扭转振型法和自由杆件扭转振动法测试的LVL 纵向剪切模量①Tab. 10 LVL longitudinal shear modulus tested by free plate torsional vibration method and free rod torsional vibration method
对于100 mm×100 mm×10.8 mm 各3 块方板,采用自由方板扭转模态法(本研究)、自由方板扭转振动法和方板静态扭转应变法测试纵向剪切模量分别为 865 MPa(1.4%)、659 MPa(1.4%)和 860 MPa(1.0%)。
从以上数据可以定量得到:
1) 随试件长宽比减少,自由方板扭转振型法和自由杆件扭转振动法测试的LVL 纵向剪切模量减小,特别对方板试件的测试值显著减小;
2) 传统自由方板扭转振动法测试的LVL 纵向剪切模量分别小于自由板扭转振型法、自由杆件扭转振动法和自由方板扭转模态法12.9%、17.0%和23.8%,即从测试精度考虑,传统自由方板扭转振动法不可用于测试木材剪切模量;
3) 自由方板扭转模态法测试的LVL 纵向剪切模量与方板静态扭转应变法测试值相当吻合,相对误差仅 0.6%;而自由板扭转振型法和自由杆件扭转振动法,若以方板为试件测试的LVL 纵向剪切模量与方板静态扭转应变法测试值的相对误差分别为-12.0%和-7.7%。
自由方板扭转模态法基于自由方板特有的一阶扭转振型特征和一阶扭转模态频率,不仅理论基础可靠,而且具有测试剪切模量精度高、试验操作方便等优点,是一种测试木材剪切模量值得推荐的好方法。
5 结论
1) 木材自由板一阶扭转振型特征与其长宽比l/b有关。对于l/b=1 的木材自由方板,其一阶扭转振型特征为:在其长边y=b/2上呈直线变化,在其宽边x=l/2上呈曲线变化,可用y的无常数项四次多项式拟合;对于长宽比l/b≥3 的木材自由板,其一阶扭转振型特征为:在其宽边x=l/2上呈直线变化,在其长边y=b/2上呈曲线变化,可用x的无常数项四次多项式进行拟合。
2) 木材剪切模量与其一阶扭转频率的关系式(2)、(3)、(4)用于推算木材主向剪切模量适用的方板宽厚比为:对于木材弦向和径向方板宽厚比分别不得小于17 和20;对于木材横向方板宽厚比则从7 到30。
3) 自由方板扭转模态法,即木材剪切模量与其一阶扭转频率的修正关系式(6)、(7)、(8)用于测试木材主向剪切模量适用的方板宽厚比,对于木材弦向、径向和横向方板均在7~30 范围内。
4) 自由方板扭转模态法既适用于测试木材主向剪切模量,又适用于测试木质复合板材和各向同性材料剪切模量,其有效性得到自由杆件扭转振动法和非对称四点弯曲法试验验证。
5) 理论分析和试验结果表明,传统自由方板扭转振动法测试木质复合材和木材剪切模量偏低,其偏低程度与材料类别和方板宽厚比有关。

