考虑氢能调峰要素的岛屿能源系统结构优化

王博弘 王长昊 邱 睿 林聿明

1. 浙江海洋大学临港石油天然气储运技术国家地方联合工程研究中心

2. 城市油气输配技术北京市重点实验室·中国石油大学（北京） 3. 国家石油天然气管网集团有限公司油气调控中心

0 引言

大多数岛屿能源负荷小，离岸距离长，依靠进口化石燃料和电网是这些岛屿能源供应的主要方式。但进口化石燃料会导致高发电成本和环境问题[1]。舟山群岛位于浙江省东北部，作为地理上孤立的区域，在确保能源供应和减少环境污染方面面临一系列挑战。浙江省提出到2025年碳排放总量和强度得到有效控制，低碳发展水平显著提升[2]。目前，浙江省一次能源消费中煤炭和石油占比80%[3]。因此，调节能源结构，使用太阳能、风能和氢能等清洁能源代替化石能源，有效减少CO2排放尤为重要。其中，氢能被认为是极具发展前景的二次能源[4-5]，具有清洁低碳、高热值、高转化率等优势。“双碳”背景下，发展氢能成为众多国家应对气候变化、实现“双碳”目标的重要选择[6]。

氢能消耗与温室气体排放总量呈负相关，是解决环境相关问题（包括有害气体排放）的最可行解决方案之一[7]。氢能是一种理想的新型能源，具有清洁、低碳、高效、可再生等优点[8-10]，其最佳利用方式是通过燃料电池技术进行氢电转化[11]。然而，由于其重量轻和气态性质，在氢气储存方面存在挑战[12]。目前常见储氢方式有4种：高压气态储氢、低温液态储氢、有机液态储氢和固体材料储氢[11]。不同的储氢方式会对储存技术的要求和储存成本产生影响。制氢的原材料不同，在氢气生产过程中所产生的CO2也不同，选择适当种类的氢能制取和储氢方式在减少碳排放和提升经济效益方面至关重要。

国内外多从能量系统的优化配置方面开展岛屿能源系统优化研究。杨晨辉[13]研究了沿海岛屿混合微电网系统的控制策略和优化配置。赵为光等[14]提出了一种新型多能互补模型的微能源网优化方法，通过调度微能源网内各设备运行方式和出力情况，以满足海岛用户对能源的需求。Ahmadipour等[15]提出了一种蝗虫算法（Grasshopper Optimization Algorithm，GOA）用于维持包含分布式能源的孤岛电力系统的稳定性。Vera等[16]建立了耦合有机朗肯循环（Organic Rankine Cycle，ORC）发电机的海洋热能转换系统模型，并将该模型用于圣布拉斯群岛（巴拿马）的能源系统的优化案例。我国大陆电网系统相对脆弱，在高负荷用电时供电量紧张[17]，且从大陆输送电能至岛屿成本过高。电网中大多采用煤热发电，污染物质和CO2排放量较高，因此，需要从经济性和碳排放量两个角度对岛屿内部能源结构进行分配和调整，实现绿色低碳转型。

本文采用碳夹点分析方法作为岛屿能源结构分析和优化的工具。夹点方法最初用于换热网络设计，其核心在于构建一种图形，用以准确描述那些复杂约束，并直观展现优化过程[18]。碳夹点分析法[19]源于夹点方法，经过不断发展创新，其应用范围已延伸至能值夹点[20]、氧夹点[21]、水夹点[22]、热能—电能夹点[23]等工程领域。Tan等[24]提出了基于夹点的碳约束能源规划方法，并首先使用数形结合的方法解决能源规划问题，通过能源曲线的平移与转化来确定过程的最小零碳能源或低碳能源用量。Crilly等[25]改进了碳夹点分析方法，使用了基于图形优化概念的新方法用于分析和规划爱尔兰发电行业。赵立华等[26]将碳夹点方法应用于多场景下能源最优分配研究，并通过进一步优化供应系统，将其对经济的影响降到最低。余鸿等[27]使用碳夹点分析法建立分析模型，以天津市为研究对象，考虑总体和区域的能源需求和碳排放约束，规划最优能源结构。碳夹点分析方法可以与数学规划模型结合，定量计算每种能源的需求量，并通过碳夹点图的方式直观展现能量的调节方式，实现能源最优规划。

基于现有文献发现，大部分研究仅采用碳夹点分析法规划某区域的能源结构，并未考虑能源消耗随季节变化的不确定性。本文以舟山群岛为例，基于碳夹点分析法优化岛屿能源系统结构，同时讨论了氢能作为储能物质的经济性和环境效益。在能源需求淡季合理储存能源，在能源旺季释放能量，在保证达到减排目标的条件下解决能量供给不均的问题。

1 碳夹点分析方法

碳夹点分析法在本文应用有两种：①在能源规划中，给定某地区碳减排目标，计算得到该目标下，各项电力能源，特别是其中清洁能源的占比；②用于季节性电力能源规划，实现调峰。

1.1 碳夹点分析步骤

1）根据往年信息收集某地区每年的发电量，假设某地电能需求量为（M＋N）GW·h，且只由能源A和能源B提供（表1）。

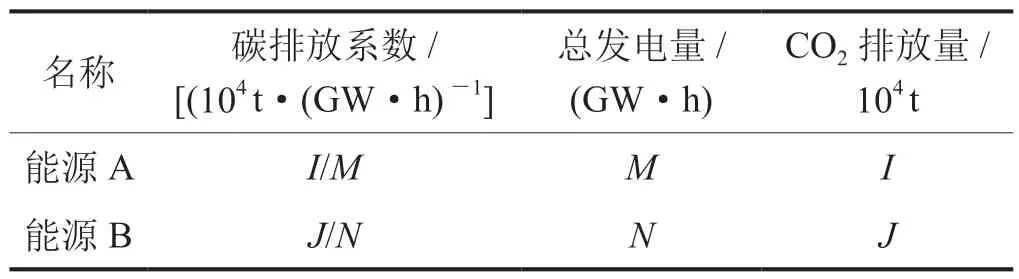
表1 某地发电量及碳排放量表

2）依照某地的需求量，画出一条过原点和（M＋N，I＋J）的需求量线段，再根据表1数据，以横坐标为能量，纵坐标为CO2排放量画出能源供应线如图1所示。

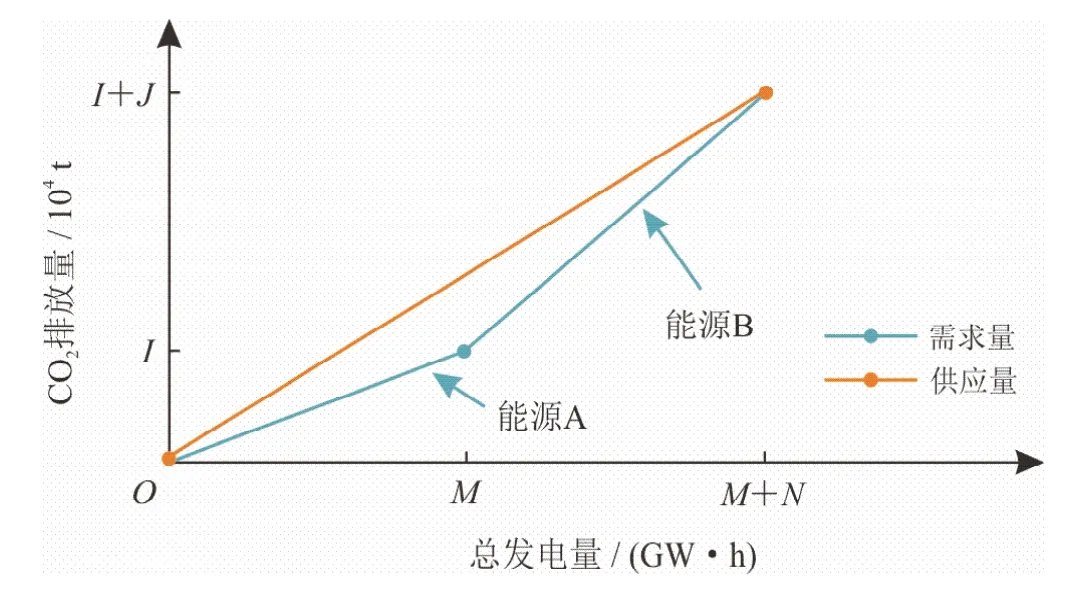
图1 供需能源图

3）设置减排目标，画出减排后的需求量线段，该线的最右端点为点a，向右平移原能源供应线使其与需求量曲线相交于点a，即为碳夹点。碳夹点以上部分，即线段ac，为需减排部分，移动原供应量折线，所移动长度Ob为所需清洁能源增加量，如图2所示。

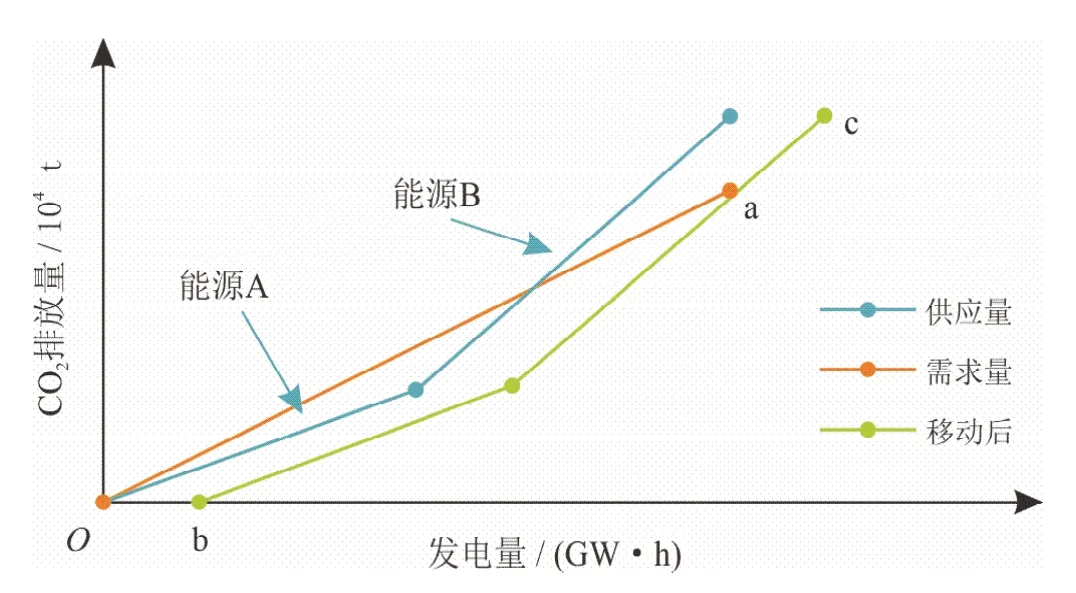
图2 碳夹点例图

4）调整能源结构，使得a点以上部分由低排放或零排放的清洁能源所提供。

1.2 模型建立

为简便计算，碳夹点分析可以通过建立数学模型的方式，计算能源的需求量。

定义数学模型如下，假设在某地区有c种能源用于发电，由能源提供电能Nj满足地区所需电能，相应的碳排放系数为ωj。

目标函数为求某低碳发电能源的最小发电量：

式中D表示能源需求量；ωj（j= 1，2，3…）表示能源j发电的碳排放因子；表示能源j的最大发电量，GW·h；Ni表示各个场景下需规划的低碳能源i的发电量，GW·h；Nj表示能源类型j的发电量，GW·h；E表示设置的CO2排放量的最大限度，kt。

2 案例分析

2.1 案例地区能源概况

从发电结构来看，2021年浙江省火力、水力、风力、核能、太阳能发电量分别占比75.52%、3.96%、1.00%、18.24%、1.28%[28]。本文假设舟山市与浙江全省发电结构相同。2021年所需总电量为13 479.65 GW·h[29]。经计算不同种类发电量和对应的CO2排放量如表2所示，其中采用煤炭为燃料的火力发电方式的碳排放因子高达888 t (CO2)/(GW·h)。通过表中数据可以发现，在发电结构中碳排放因子最小3种发电方式为水力、风力和太阳能发电，但三者在当前能源结构中占比很小，具有巨大的提升潜力以降低碳排放。根据《浙江省可再生能源发展“十四五”规划》[30]，该省海上风电装机从186×104kW·h增加到641×104kW·h，增加到原来的3.45倍；光伏装机从1 517×104kW·h增加到2 750×104kW·h，增加到原来的1.81倍；水电装机全省从1 171×104kW·h增加到1 526×104kW·h，增加到原来的1.30倍。上述规划目标可作为碳夹点分析的约束条件。如图3所示，根据碳排放因子大小，从小到达排列画出供应量复合曲线，连接首端和末端即为需求量线。

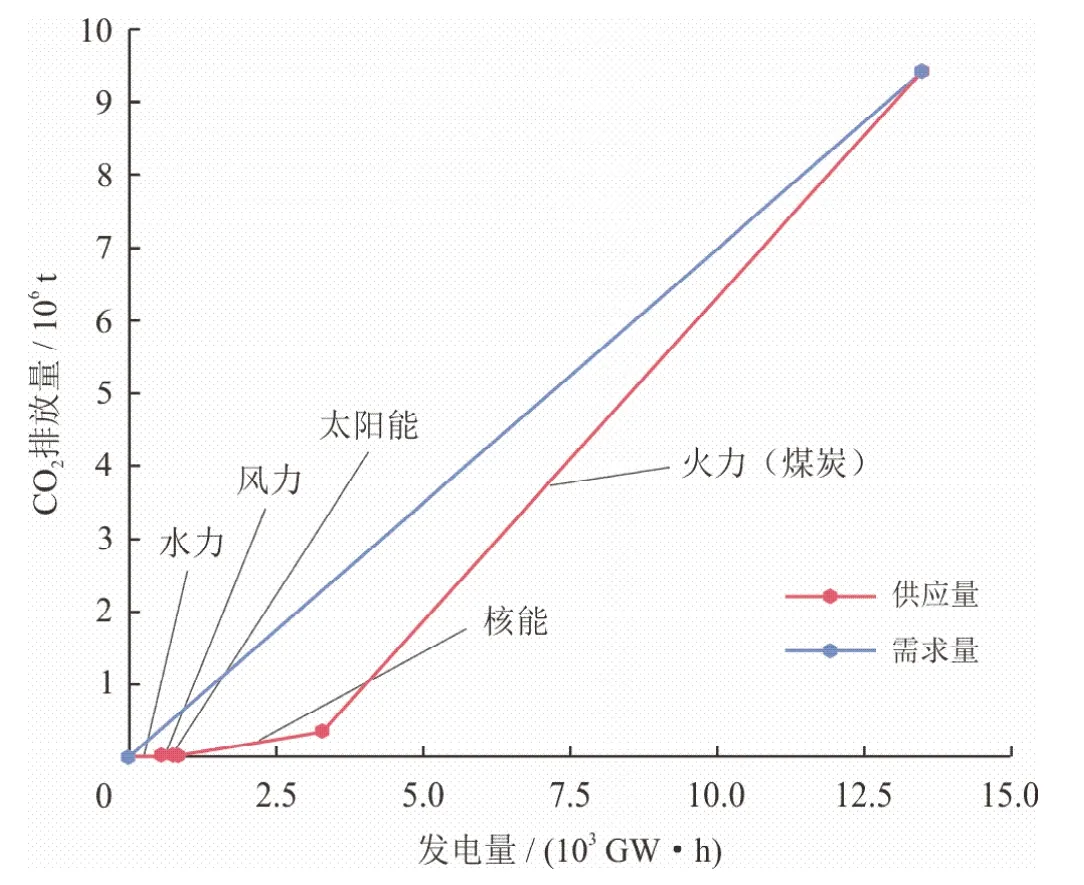
图3 供需夹点图

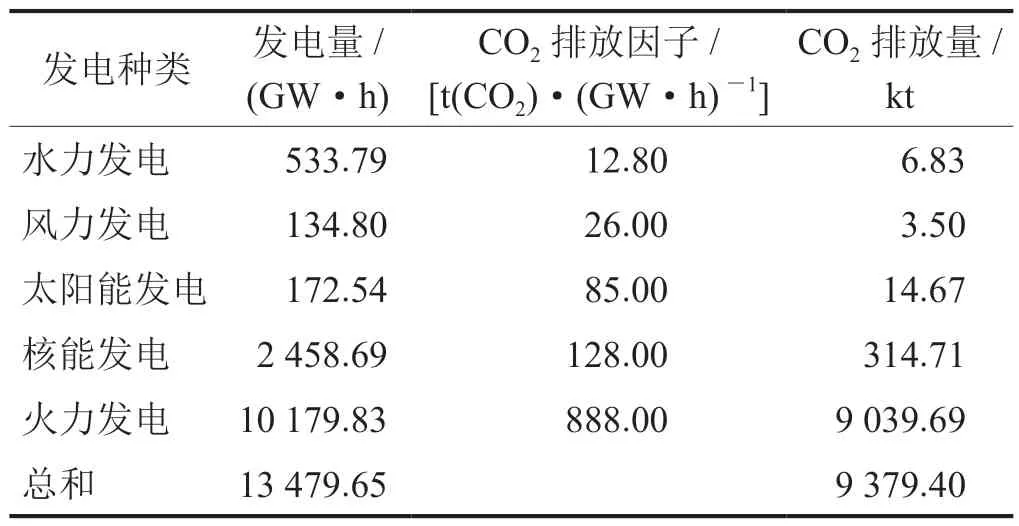
表2 2021年舟山市CO2排放量表

2.2 调整方案

浙江省“十四五”节能减排综合工作方案指出，到2025年，全省单位生产总值能源消耗比2020年下降14.5%[35]，本文以此作为减排目标。

首先，设置减排14.5%的目标，画出减排后的能源需求线。如图4所示，平移原能源供应线使得原能源供应线过能源需求线最右点（点e），此交点即碳夹点。夹点右上方线段表示需减排1 003.61 kt CO2以完成减排目标。为达到该减排目标，e点以上火力发电部分需使用清洁能源代替，以实现在满足发电量的前提下减少碳排放量。此时有3种方案：方案一使用水力发电代替，设置太阳能发电约束量不超过2021年发电量的1.81倍，风力发电不超过2021年发电量的3.45倍；方案二使用风能发电代替，设置水力发电约束量为不超过2021年发电量的1.3倍，太阳能发电不超过2021年发电量的1.81倍；方案三使用太阳能代替，设置水力发电约束量为不超过2021年发电量的1.3倍，风力发电不超过2021年发电量的3.45倍。

3个方案经计算如表3所示，方案一共需增加水力发电1 100.60 GW·h；方案二需1 285.13 GW·h风力发电代替火力发电；方案三需1 164.79 GW·h太阳能发电代替火力发电，上述3个方案都可以达到所设置的减排14.5%的目标。图5展示了原方案和3个减排方案对应的碳夹点图。

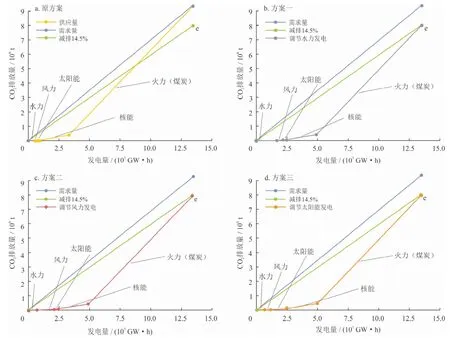
图5 原方案和3个减排方案对应的碳夹点图

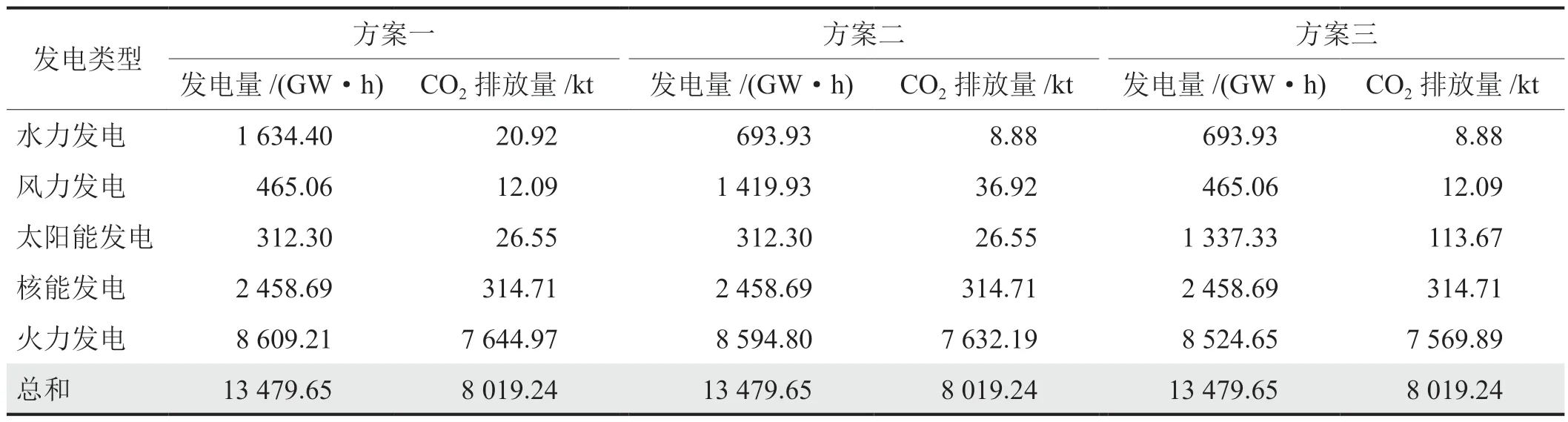
表3 各减排方案发电量及CO2排放量表

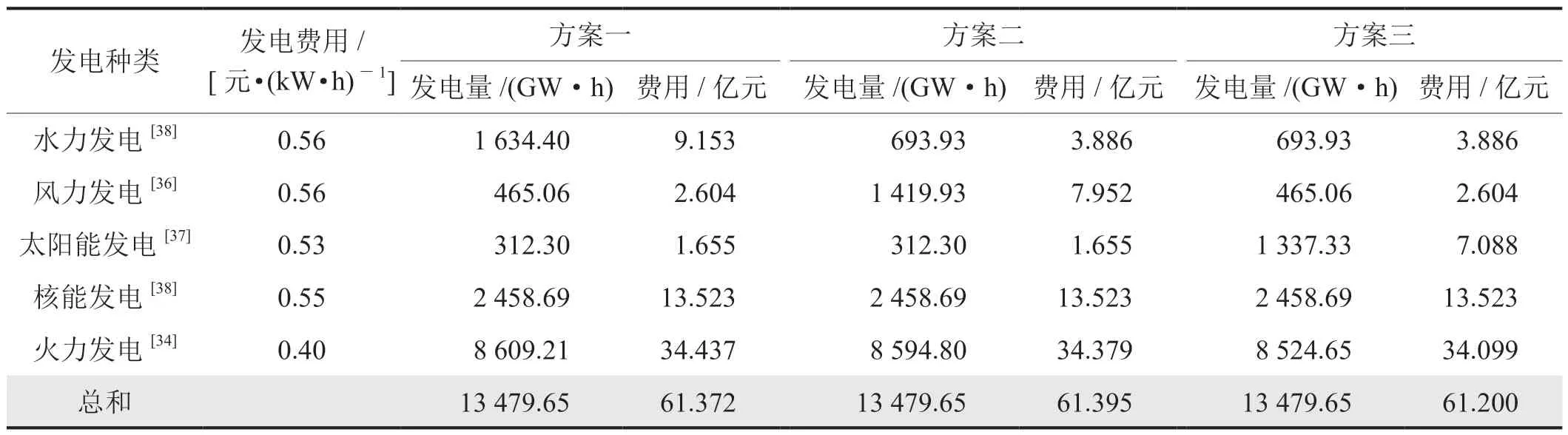
表4 发电成本费用表

2.3 经济核算

海上风力发电的成本为0.56元/(kW·h)[36]，太阳能发电0.3元/(kW·h)[37]，火电的发电成本是0.4元/(kW·h)[34]，水力发电成本约为0.56元/(kW·h)，核电平均成本为0.55/(kW·h)[38]。具体发电成本如表5所示，本文考虑到核电站不易扩建，在能源规划中不再增加核能发电。

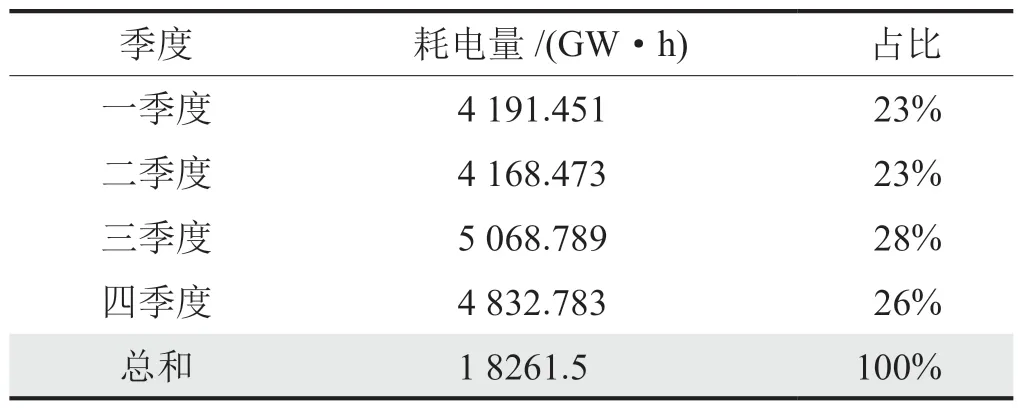
表5 2022年舟山市季度电能消耗表

通过数据分析，3种方案中方案三（调节太阳能发电量）的费用最低，方案一（调节水力发电量）和方案二（调节风力发电量）费用相近，仅相差230万元。费用最低的方案三相对费用最高的方案二相差1 950万元，仅低0.3%左右，由此可以得出，在未来发电成本改变不大时，可优先发展太阳能发电、风力发电和水力发电结合发展。

2.4 季节性能源调整

岛屿的社会总用电量随季节的更替发生改变。如表5所示，舟山市2022年每季度电能消耗中呈现三四季度消耗多，一二季度电能消耗少的情景。其中一二季度消耗电能较少，约占全年消耗的46%；三四季度耗能较多，占全年消耗的54%。笔者据此用电特征规划舟山市的季节发电量。

为避免因能源季节需求量不同，而产生能源浪费和能源供应不足的问题，本文采用氢能调峰，并通过碳夹点分析法计算需用于调峰的氢能量。如图6所示，以最具有经济性的方案三（太阳能发电）为例，对三、四季度的用电量进行碳夹点规划，由于电能需求量高于供应量，需要计算所需额外发电量。在本案例中，将三、四季度供应量复合曲线向右移动直至与需求量线交于点e，复合曲线平移距离即为所需氢能发电量。经计算需要通过氢能发电539.19 GW·h。

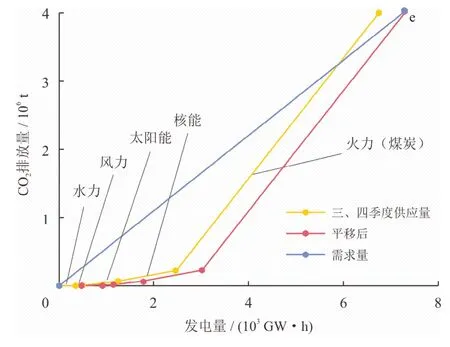
图6 三、四季度碳夹点图

水力发电、风力发电以及太阳能发电等新能源发电不稳定，气候条件的变化会导致发电量出现较大波动[39]。在电能需求量小的季节时会出现弃电，为防止电能的浪费可以将这部分弃电用于制氢和储氢。如利用化石燃料制氢、电解水制氢，以及压缩储存氢气。

在制氢方式选择中，当前全球生产的氢气96%来自化石能源，仅4%来自电解氢。天然气制氢成本12 831元/t，煤制氢9 903元/t[40-41]。电解水制取氢气的成本与电价相关，当电价0.55元/(kW·h)时制氢成本为33元/kg[42]。虽然使用绿电电解水制氢碳排放接近于0，但由于成本过高在近些年中很难实现大规模利用。舟山市天然气利用量较少，2021中规模以上工业主要能源消费量[43]包括气态天然气4 411×104m3，液化天然气5370 t，原煤135.5×108t。因此通过煤化工制氢，将煤转化为氢气储存，是合理的制氢调峰方式。1kg氢气的热值约等于33 kW·h电量，氢燃料电池热值效率随着负载设定值为42.5%～74.08%[44]。本文以中间值58%计算，1 kg氢气可发电19.14 kW·h，即需要在一二季度制取28.17 kt氢气以满足调峰需求。通过适当的煤制氢的方法制取1 kg氢气排放9.33 kg (CO2)[45]，煤制氢成本在7.2～10.1元/kg[46]，取平均值8.65元/kg进行经济核算，共需2.44亿元。

在储氢方式的选择中，多名学者[47-49]对现有技术进行了分析，认为有机液态储氢成本上过高；固体材料储氢仍处应用不成熟的阶段；压缩氢气是一种成熟的技术，并且对于固定目的，例如在氢气发电厂中使用，是经济可靠的存储方法[12]。因此本案例在氢能的储存方式中选择压缩氢储氢。已有研究对压缩气体（地上和地下）分析了技术经济可行性，其中地下中的压缩气体储存成本最低[50]。因此本文案例亦选用地下压缩气体的方式储存氢气。

盐穴、贫竭碳氢化合物储层和盐水层每公斤氢气的平均成本别为1.61、1.23和2.77美元[51-52]。假设三者的平均值作为储氢成本，经计算平均每公斤氢气1.87美元，折合人民币12元/kg。经计算共需3.38亿元作为储氢费用。在氢能投资中涉及制取费用和储存费用，共5.82亿元。经计算全年费用以及发电量如表6所示，总需费用64.572亿元，比原计划（方案三）增加3.372亿元。在引入氢能调峰后舟山市的发电成本增加5.5%，其中制氢费用占2.3%，储氢费用占3.2%。未来随着储氢和制氢的技术发展，氢能调峰的成本会不断降低。

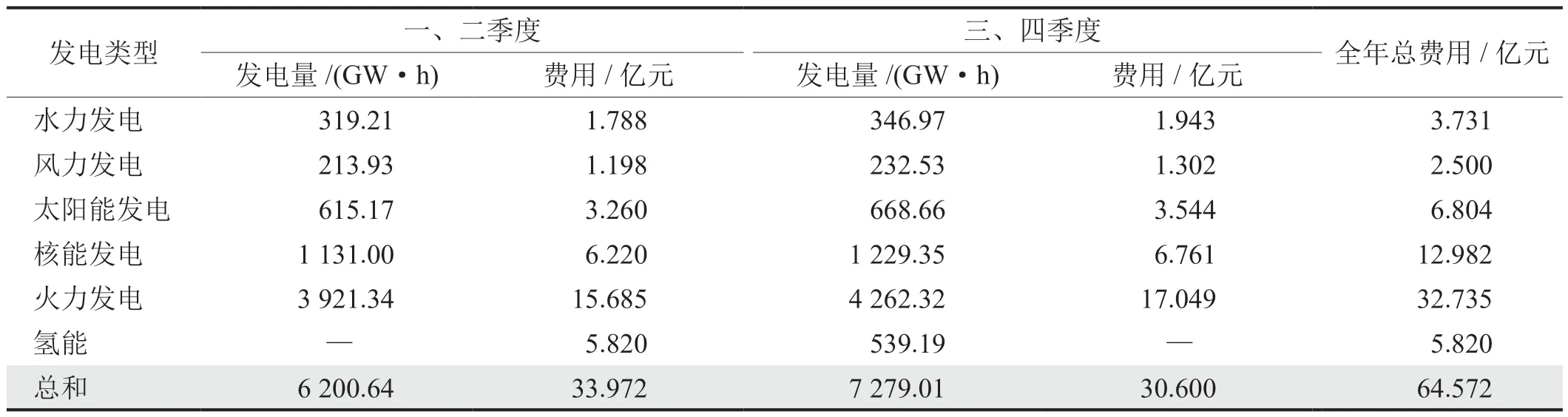
表6 全年发电量及发电费用表

3 结论

1）应用碳夹点分析法对岛屿能源系统进行规划，首先使用图解法建立“横坐标为能量，纵坐标为碳排放量”的坐标系，直观展示研究地区能量需求和对应碳排放量；通过平移能源供应线的方式寻找碳夹点，确定应减排能源量，进而得到满足条件的能源减排方案。

2）根据舟山市电力减排目标，即相对2021年减排CO214.5%，使用碳夹点分析法计算了水力发电、风能发电、太阳能发电3个方案所需增加的新能源发电量，以替代火力发电。结果显示：方案一（水力发电）需要增加1 100.60 GW·h水力发电代替火力发电，方案二（风力发电）增加1 285.13 GW·h风力发电代替火力发电，方案三（太阳能发电）增加1 164.79 GW·h太阳能发电代替火力发电。

3）以减排14.5%为目标，考虑制氢成本和储氢成本，全年氢能投资成本为5.82亿元。提出的调峰方案解决了一、二季度能源消耗量较少而电力消纳不足的问题，避免能源浪费。在能源需求量较少的一、二季度制取28.17 kt氢气用于三、四季度，可以解决用电高峰季节的能源短缺，使上、下半年都可以达到14.5%的减排目标。

4）分析了新增水力发电、风力发电、太阳能发电的经济性，结果表明增加太阳能发电是最经济的调节方式，全年共花费61.2亿元，但优势不明显，相比其他方案仅低0.3%左右，应在条件允许的情况下优先发展太阳能发电，在条件受限时发展风力发电和水力发电也同样具有优势。