盾构隧道纵向等效抗扭刚度与抗扭性能研究

刘颖彬，廖少明，刘孟波，陈立生，徐伟忠，华建雄，刘浩

(1.同济大学 地下建筑与工程系，上海，200092；2.上海城建市政工程 (集团)有限公司，上海，200065；3.济南轨道交通集团有限公司，山东 济南，250101)

随着城市轨道交通的发展，盾构隧道的应用越来越广泛。盾构隧道是在纵向及环向通过螺栓将管片拼接而成的筒体结构，由于接头和管片的刚度差异较大，在接缝处隧道整体刚度会有较大幅度降低。外部作用可能会导致盾构隧道产生不均匀纵向沉降[1-3]，甚至产生不均匀纵向扭转[4-12]。盾构隧道纵向不均匀沉降问题在工程界已得到了充足的关注，但针对盾构隧道扭转效应的研究还较少。

盾构隧道的纵向不均匀扭转往往伴随着外部非对称荷载的出现而产生，此类非对称荷载来源包括附近土体开挖、地面偏载作用、地裂缝以及盾构纠偏等工况。彭建兵等[4-5]通过相似比试验，研究了隧道斜穿地裂缝的变形破坏机制，发现隧道衬砌结构破坏模式为扭转、弯曲、剪切变形破坏；SHEN 等[6-7]采用有限元方法分析双圆盾构施工纠偏引起的双圆隧道衬砌扭转效应；CHEN等[8-9]通过现场实测和数值模型分析了盾构斜穿引起的既有隧道轨道倾斜和截面扭转纵向分布规律，并发现当盾构小角度斜穿既有隧道时，隧道扭转极易产生；ZHENG 等[10]基于实测分析得到了基坑开挖引起的邻近隧道的扭转变形；LIU等[12]基于实时监测，分析了双圆隧道在盾构下穿过程中的结构响应，发现盾构穿越会导致既有双圆隧道产生横向扭转变形和纵向不均匀扭转，且由扭转引起的螺栓附加应力以及轨道横向倾斜严重。由此可见，不均匀扭转会导致盾构隧道受到附加应力，甚至会引起环缝渗漏水、螺栓脱落、轨道过度倾斜等病害，威胁地铁列车运营安全。因此，有必要分析盾构隧道纵向不均匀扭转下的特征。

在之前的研究中，一些研究者提出了许多纵向结构模型来考虑隧道的纵向受力性能，其中最典型的有KOIZUMI 等[13]提出的梁弹簧模型和SHIBA 等[14]提出的纵向连续模型。纵向等效连续化模型认为隧道在横向为1个均质圆环，在纵向上把由接头和管片组成的盾构隧道等效为具有相同刚度和结构特性的均匀连续梁[15]。该方法大幅简化了复杂拼接管片结构的计算，不少学者在等效连续化模型中考虑了横向刚度[16-18]和材料的非线性[19]等，并将圆形截面的计算方法用于类矩形截面计算[20-21]。WU等[22-23]基于等效连续化模型推导了隧道纵向抗剪刚度。综上所述，目前国内外对隧道纵向性能的研究主要集中于抗弯以及抗剪方面，对盾构隧道纵向不均匀扭转问题以及纵向抗扭刚度的研究较少。而事实上，抗扭问题是管片隧道结构安全的不可分割的重要组成部分。

为揭示盾构隧道纵向抗扭性能，本文首先基于等效连续化模型，分别考虑隧道管片和环缝的不同扭转变形模式及相互关系，推导不同受力组合下的盾构隧道纵向抗扭刚度的解析方法。其次，采用有限元模拟对解析解进行分析验证；最后，基于解析解，研究管片厚径比、宽径比、螺栓有效长度以及纵向轴力和弯矩等关键参数对纵向等效抗扭刚度的影响。

1 盾构隧道纵向抗扭刚度推导

1.1 基本假设

在弯-剪作用基础上，盾构隧道叠加扭转作用后的受力状态将极为复杂。为便于推导并不失一般性，基于等效连续模型，以盾构隧道相邻2个半环及环缝为1 个计算单元(如图1(a)和(b)所示)，推导盾构隧道纵向抗扭刚度。进一步作出如下基本假定：

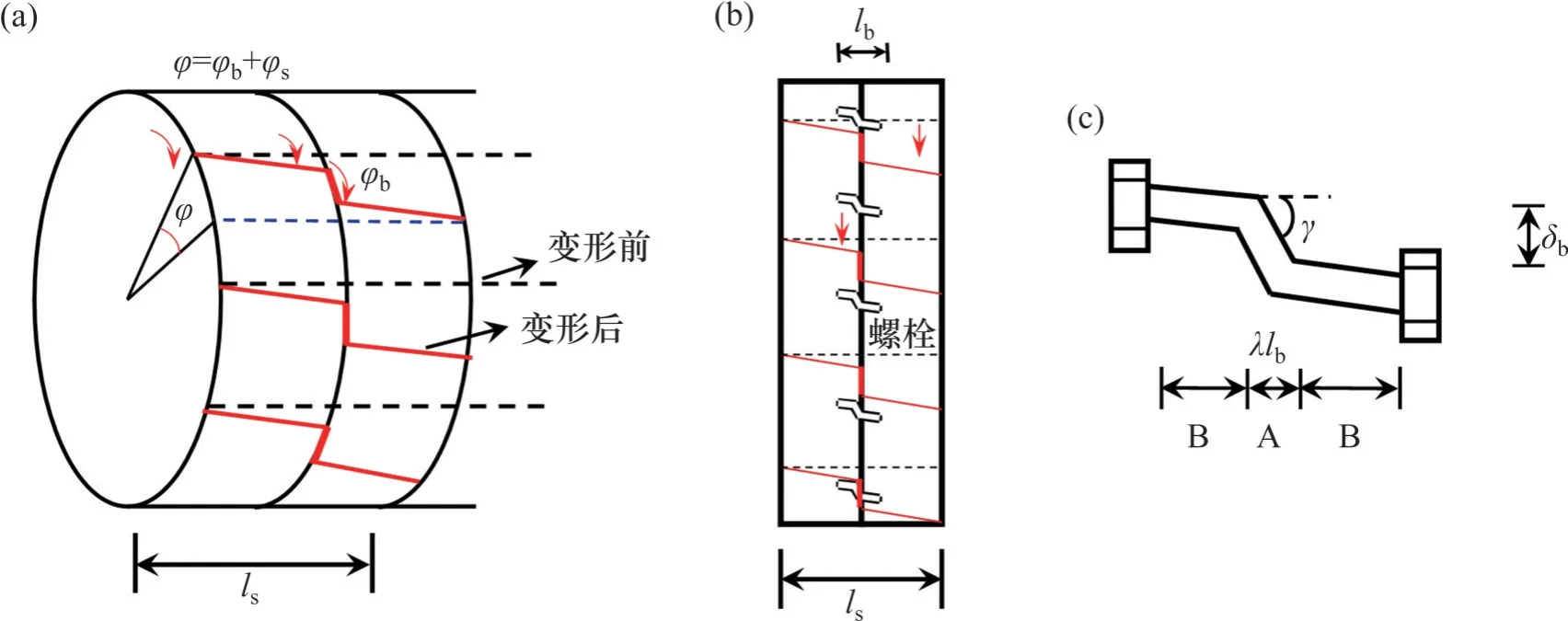
图1 隧道单元扭转变形模式图Fig.1 Torsional deformation modes of a shield tunnel

1) 隧道横截面符合平截面假定，即横截面始终保持平面。

2) 截面中性轴位置和各点的应力分布形式沿隧道纵向保持一致。

3) 设钢筋混凝土管片环宽为ls，螺栓的长度为lb，螺栓沿圆周均匀分布。在螺栓长度lb范围内，隧道纵向弯矩作用下产生的压力由管片承担，拉力由螺栓承担；在螺栓长度范围外，隧道纵向弯矩作用下产生的压力和拉力均由管片承担。在扭矩作用下，环缝处扭矩由螺栓及环缝摩擦共同承担，环缝外扭矩则由管片承担。

4) 不考虑凹凸榫、错台变形以及管片拼装形式等对结构抗扭的影响。

1.2 等效抗扭刚度定义

基于上述假定，计算单元的截面扭转角由环缝扭转角和管片扭转角2个部分组成。则单元总扭转角的计算公式为

式中：φ为单元总扭转角；φb为接缝的扭转角；φs为管片的扭转角。

单元等效的相对扭转角θ为

隧道的等效抗扭刚度(GI)eq为

式中：T为扭矩；(GI)s为隧道管片的抗扭刚度；ξ为纵向等效抗扭刚度有效率。

从式(1)可知，接缝抗扭性能对隧道等效抗扭刚度影响很大，而接缝扭转在很大程度上又受到螺栓的影响。为进一步考虑螺栓的影响，根据何川等[24]的足尺试验结果，引入螺栓有效剪切长度系数λ。如图1(c)所示，假设在λlb范围内(A)，接缝处扭矩由该部分螺栓承担，而其余部分(B)与管片协同变形，则有φs=θs(ls-λlb)，其中θs为管片的相对扭转角。

根据以上假设，纵向螺栓的抗剪方程和抗扭方程为：

式中：Kb为等效剪切刚度，Kb=κbGbAb/(λlb)；κb为螺栓的剪切修正系数，κb=0.9；Fbi为单个螺栓剪切力；Tb为螺栓产生的扭矩；Ab为螺栓的截面积；Gb为螺栓的剪切刚度模量；ρbi为螺栓i距扭转中心的距离，，a为接缝处扭转中心距隧道中心的距离；Rb为螺栓距离隧道中心的距离；δbi为螺栓i的剪切变形，δbi=φbρbi；db为螺栓的直径；γ为螺栓的剪切角；n为纵向螺栓个数。各参数含义如图2所示。可得到环缝的平均抗剪线刚度Kt为

图2 接缝扭转受力分布图Fig.2 Stress distribution on circumferential joint

螺栓总抗剪切力和扭矩可由下式表达：

1.3 不同受力状态及其组合下隧道抗扭刚度

工程实践与现场实测结果表明，盾构隧道在受到外部非对称荷载时会同时产生弯、剪、扭等结构响应[8-12]，且相互影响。因此，本文从纯扭的理想状态出发，对复杂压-弯-扭组合作用下的隧道等效连续化抗扭刚度进行推导。

1.3.1 纯扭状态

1) 管片扭转变形模式。将单环管片视为均质结构，则其扭转模式不受受力状态的影响。因此，仅在此节说明单环管片的扭转变形模式。根据受力平衡条件，可得到管片扭转变形和扭矩的关系式：

2) 环缝扭转变形模式。在纯扭状态下，环缝混凝土无抗扭摩擦力，环缝的扭矩全由螺栓提供。环缝处受力平衡条件为

由于螺栓沿中心对称，扭转中心即为隧道中心，螺栓抗剪切力的总矢量之和为0。单螺栓剪切力和总扭矩的计算公式可简化为

3) 等效抗扭刚度计算。根据受力平衡条件，联立式(8)～(10)，可得到接缝扭转角、等效抗扭刚度和抗扭刚度有效率为

1.3.2 压扭组合

1) 环缝扭转变形模式。环缝处受力平衡条件为

在压扭情况下，在环缝处压应力均匀分布且具有对称性，因此，环缝处剪力之和总等于0。受压混凝土产生的摩擦抗扭矩Tc可由下式得到：

式中：fc为接缝处相邻管片的摩擦因数；Fc为受压混凝土产生的摩擦剪力；σc为接缝混凝土压应力；t为衬砌环厚度；ρc为混凝土单元距离扭转中心的距离，。

2) 等效抗扭刚度计算。根据受力平衡条件，联立式(10)、(12)和(13)，可得到接缝扭转角和等效抗扭刚度为

1.3.3 弯扭组合

1) 环缝扭转变形模式。在弯扭组合状态下，环缝一侧受拉、一侧受压，受压侧产生的压应力一方面会产生抗扭的摩擦力，另一方面会导致环缝处扭转中心发生偏移，使之往受压侧偏移，如图2 所示。管片受力是沿竖直轴对称分布的，因此，扭转中心必在竖直轴上。令扭转中心与截面中心的距离为a。弯-扭受力状态下环缝内的应力和变形分布情况见图3。

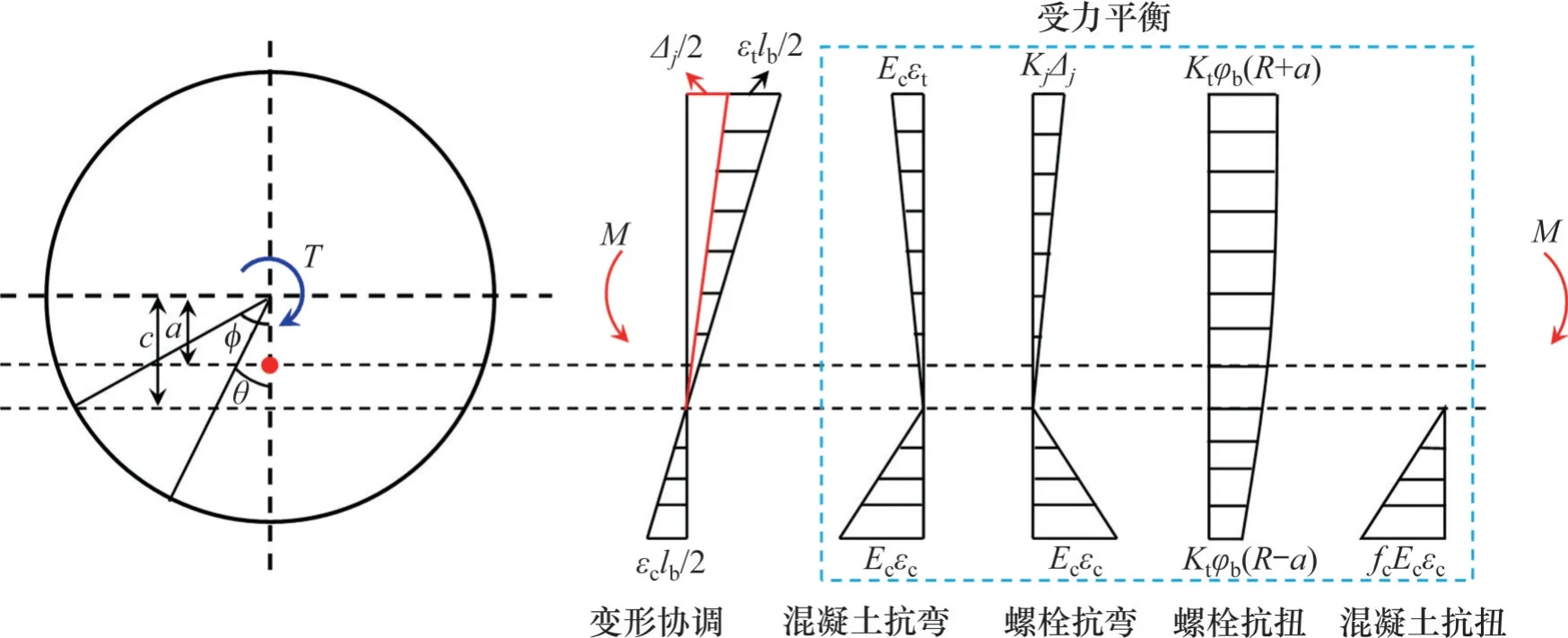
图3 弯扭状态下环缝内的应力和变形Fig.3 Stress and deformation of circumferential joints under bending and twisting conditions

根据变形协调条件可得：

式中：εt和εc分别为管片接头的最大拉应变和最大压应变；Δj为距离中性轴最远处的环缝张开量；αj为环缝范围内的转角；c为中性轴与轴线的距离；ϕ为中性轴与轴线的夹角，且有c=Rcosϕ。

根据轴力平衡条件有：

式中：Ec为混凝土弹性模量；Kr为螺栓的平均抗拉线刚度，Kr=nEbAb/(2πRblb)，Eb为螺栓弹性模量。

根据弯矩平衡条件有

环缝处剪切平衡条件为

由于环缝处压应力和螺栓均关于竖直轴对称，故

则式(20)可改写为

其中，螺栓和混凝土摩擦剪切力表达式为

式中：α为计算单元与扭转中心连线与竖直线的夹角，如图3所示，且有。

扭矩平衡条件为

受压混凝土产生的摩擦抗扭矩为

由螺栓产生的扭矩为

2) 等效抗扭刚度计算。根据受力平衡条件，联立式(15)～(27)，可得到扭转中心的位置、接缝扭转角和等效抗扭刚度：

1.3.4 压弯扭组合

结构受到压-弯-扭组合受力时，中性轴位置将出现2种情况[25]，以下将分别讨论。

1) 中性轴在截面内。在环缝张开的条件下，环缝内的应力和变形分布情况如图4 所示。从图4可知，该条件下的变形协调条件、剪切平衡条件、扭矩平衡条件以及等效抗扭刚度计算均与1.3.3 节中的弯扭组合一致，计算方法见公式(15)、(16)和(20)～(28)。

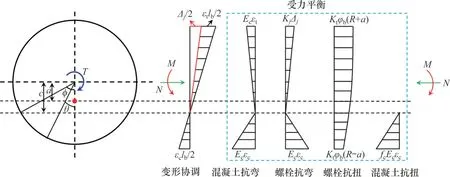
图4 环缝内的应力和变形分布(环缝张开)Fig.4 Stress and deformation distribution of circumferential joints with opening

根据轴力平衡条件有：

根据弯矩平衡条件有：

2) 中性轴在截面外。在环缝闭合的条件下，环缝内的应力和变形分布情况如图5所示。

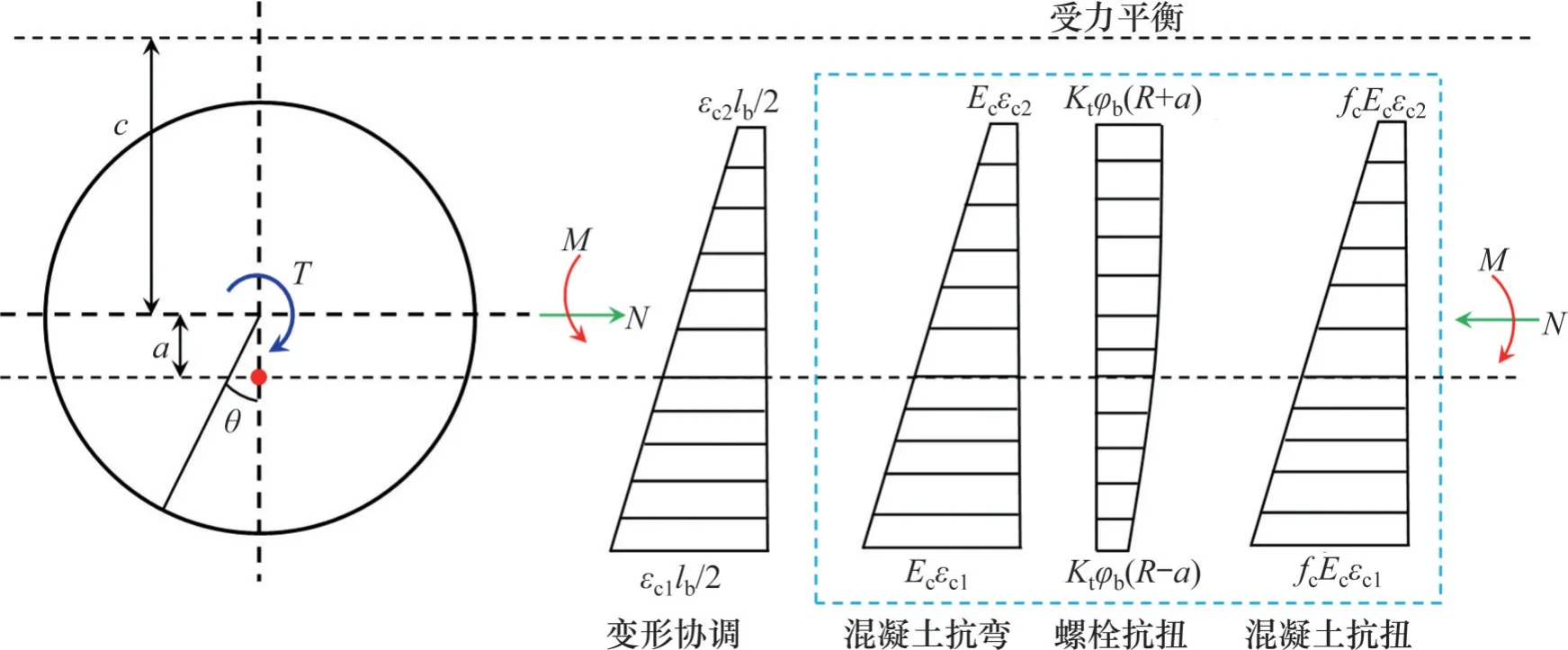
图5 环缝内的应力和变形分布(环缝闭合)Fig.5 Stress and deformation distribution within range of closed circumferential joints

根据变形协调条件可得：

式中：εc1和εc2分别为接缝混凝土的最大压应变和最小压应变。

根据轴力平衡条件可得：

根据弯矩平衡条件可得：

剪切平衡条件同式(22)，Fbx参见式(23)，Fcx参见式(24)。扭矩平衡条件同式(25)，Tc参见式(26)，Tb参见式(27)。等效抗扭刚度计算参见式(28)。

以上给出了不同受力状态下的盾构隧道纵向等效抗扭刚度的解析解。获取螺栓有效剪切长度是求解盾构隧道纵向抗扭刚度的关键。肖时辉等[26]基于理论解析和足尺试验的对照结果，得出螺栓有效剪切长度约为装配手孔的纵向长度的3倍。但由于螺栓孔构造复杂，要确定不同管片的螺栓有效剪切长度系数需要进行更多研究。

2 与数值模型试验的对比

本节采用三维数值模拟方法，分析不同受力状态下隧道的纵向抗扭性能，并与本文提出的抗扭刚度解析解进行对比验证。

2.1 有限元模型建立

1) 管片隧道模型与参数。本文采用ABAQUS有限元软件建立三维精细化数值计算模型，采用实体单元C3D8R 来描述衬砌和螺栓的力学行为。以深圳某地铁隧道管片为例，有限元模型参数如表1所示，管片接头构造及管片隧道数值模型分别如图6和图7所示。

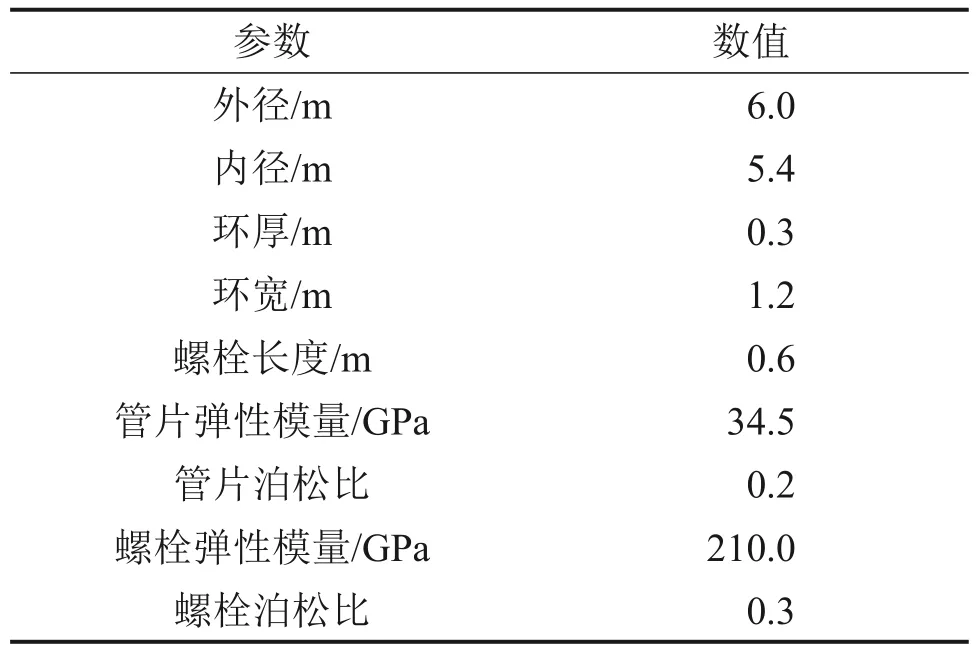
表1 有限元模型参数表Table 1 Parameters of FEM model

图6 管片衬砌俯视图Fig.6 Planform of the segmental ring

图7 管片数值模型网格划分图Fig.7 Meshing of segmental rings

2) 接触设置。螺母与混凝土之间的接触通过绑定约束实现，螺杆与螺栓孔之间、管片与管片之间均采用面对面接触，其中法向接触是硬接触，只受压不受拉；切向接触采用拉格朗日函数来模拟。

3) 边界条件和加载方式。管片左侧设为自由端，约束右侧管片右端所有方向的位移。边界约束为节点约束，如图8所示。采用分级加载的方式施加扭矩荷载，加载情况如下。

图8 有限元模型边界约束条件和加载示意图Fig.8 Boundary constraints and loading of FEM model

① 纯扭作用。扭矩采用分级加载，逐步增大扭矩。

② 压扭组合作用。端面施加固定轴力，扭矩采用分级加载，逐步增大扭矩。

③ 弯扭组合作用。端面施加固定弯矩，扭矩采用分级加载，逐步增大扭矩。

2.2 结果验证

基于有限元模型输出管片环扭转变形和环缝扭转变形，采用式(3)可计算得到数值模型中盾构隧道的等效抗扭刚度及其有效率。图9所示为纵向抗扭刚度有效率的数值解和本文提出的解析解的对比。从图9可见：抗扭刚度有效率的数值结果和理论结果较吻合，相对误差小于5%，验证了本文提出的等效抗扭刚度解析解的有效性。在纯扭状态下，结构等效抗扭刚度不随扭矩的变化而变化，而是保持定值，即在纯扭状态下，接缝的抗扭性能仅由螺栓的抗扭性能决定，验证了式(11)的合理性；在压扭或者弯扭状态下，隧道抗扭刚度会随着压扭比或弯扭比减小而减小，这是因为环缝混凝土摩擦提供的抗扭力有限，而随着扭矩增大，螺栓的抗扭性能逐渐成为主导因素，验证了本文式(14)和(28)的合理性。

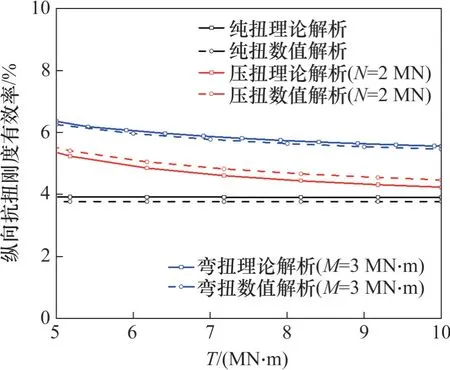
图9 纵向抗扭刚度有效率数值解和解析解对照Fig.9 Comparison of longitudinal torsional stiffness efficiency between analytical solution and numerical results

图10 所示为有限元模型中管片和螺栓的变形结果。由图10(a)可以看出：由扭转引起的单管片变形沿纵向变形差异较小，而相邻管片之间的差异变形较大，符合盾构隧道拼接结构的特性，即接缝位置刚度小、变形大，因此，差异变形主要发生在环缝位置。从图10(b)和10(c)可以看出：其螺栓的变形模式和规律与图1所示的螺栓简化模型相符；同时，数值模拟分析得到螺栓的等效剪切长度(图中标红的长度范围)约为螺栓长度的1/3，可为解析解取值提供依据。图10(b)和10(c)中各螺栓在纯扭状态下的变形基本一致，进一步验证了本文关于螺栓变形的基本假设。

图10 有限元模型变形输出结果(以纯扭T=5 MN·m为例)Fig.10 Calculated deformation of FEM(taking T=5 MN·m as an example

3 盾构隧道抗扭性能的影响因素

为探析盾构隧道抗扭性能及刚度的变化规律，便于工程应用，进一步分析隧道纵向抗扭界限、管片厚径比、宽径比、螺栓剪切长度、纵向轴力和弯矩对纵向抗扭刚度的影响。

3.1 抗扭界限

当环缝面受所外扭矩T小于环缝面摩擦能提供的最大抗扭扭矩Tc时，环缝将不发生相对扭转；当T＞Tc时，环缝开始发生转动，螺栓也将开始发挥抗扭作用。由于摩擦抵抗扭矩随环缝面受力状态变化而变化，因此，可将导致环缝转动时的外扭矩视为环缝启动扭矩，而与之相对应的抗扭摩擦源弯矩-轴力对(N，M)为自抗扭临界荷载。图11所示为当环缝启动扭矩为1 MN·m 时的轴力和弯矩(N0，M0)包络图(红色包络线)。该包络线呈现典型的凸腹状分布。当环缝所受弯矩-轴力对(N，M)在临界荷载(N0，M0)包络线内时，接缝面摩擦提供的抗扭矩不足以抵抗外荷载扭矩(Tc＜T)，环缝发生扭转，则隧道等效抗扭刚度有效率小于1；反之，接缝面摩擦提供的抗扭矩大于外扭矩(Tc＞T)，环缝不发生扭转，其抗扭可按无缝的均质结构考虑。同时，随着轴弯比N/M增大，中性轴的位置从截面下方(蓝虚线以上区域)逐渐发展到截面外(黑虚线以下区域)。

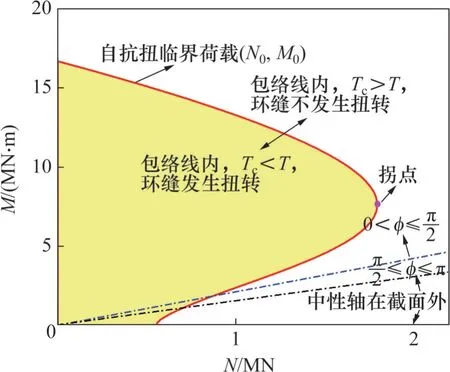
图11 隧道抗扭临界荷载(N0，M0)包络图(以环缝扭转启动扭矩为1 MN·m为例)Fig.11 Envelope curve of tunnel active-torsion-rejection critical load (taking external torque of 1 MN·m as an example)

3.2 管片尺寸

图12 所示为管片尺寸对隧道纵向抗扭刚度的影响曲线图。从图12可以看出：随着管片厚径比t/D增大，隧道纵向抗扭刚度有效率下降。这是因为增大管片厚度虽然提升了管片的刚度，但环缝面及螺栓抗扭刚度不变，导致抗扭刚度有效率下降。从图12可进一步看出：随着管片环宽与直径比l/D增大，纵向抗扭刚度提升。这是因为管片环宽越大，结构的整体刚度越大，受环缝削弱作用越小。

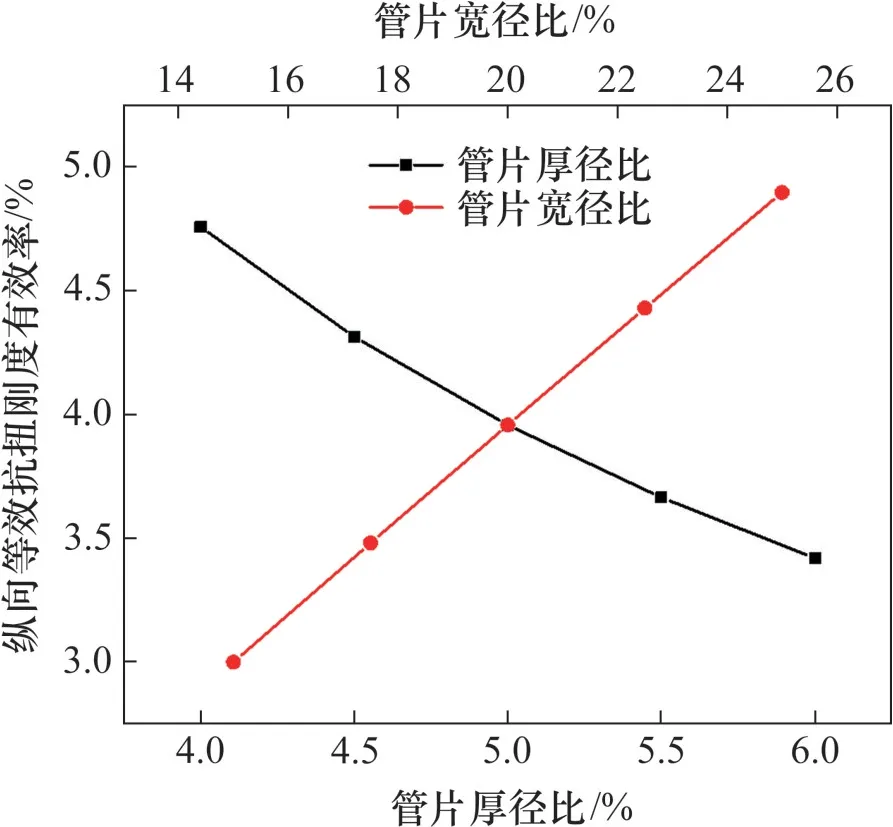
图12 管片尺寸对隧道纵向抗扭刚度的影响Fig.12 Effect of segment size on longitudinal torsional stiffness efficiency

3.3 螺栓等效长度

图13 所示为螺栓等效长度对隧道纵向抗扭刚度的影响曲线图。从图13 可以看出：隧道纵向等效抗扭刚度与螺栓等效剪切长度呈非线性负相关系；当λ减小时，纵向螺栓的平均线剪切刚度反而增大，导致环缝变形减小，隧道的等效抗扭刚度提升；当λ=0时，纵向螺栓的平均线剪切刚度可视为无穷大，则此时结构的抗扭性能即可视为无缝的均质结构。反之，随着螺栓等效长度增大，纵向螺栓的平均线剪切刚度越小，整体刚度在接缝处削弱效应越大，管片的等效抗扭刚度就越小。从图13 可进一步得到：扭转中心位置与螺栓等效剪切长度无关，说明在弯扭状态下，螺栓等效剪切长度对扭转中心的位置无影响。这与螺栓等效剪切长度不影响隧道中性轴的位置有关。因此，螺栓等效剪切长度对中性轴位置、扭转中心位置等截面性质没有影响，仅决定环缝的扭转变形。

图13 螺栓等效长度对隧道纵向抗扭性能的影响Fig.13 Effect of bolt effective length on longitudinal torsional performance

3.4 压扭比

图14 所示为压扭组合状态下压扭比对隧道等效抗扭刚度的影响曲线图。从图14 可见：在纯扭状态下，等效抗扭刚度有效率约为4%；而当压扭比N/T大于临界比(N/T)cr(即0.58 m-1)时，等效抗扭刚度有效率为100%；当N/T＜(N/T)cr时，抗扭刚度与压扭比呈现非线性正相关关系，特别是当N/T＞0.3 时，抗扭刚度有效率陡然增加，这说明隧道的抗扭性能对纵向轴力十分敏感。因此，无论是盾构隧道施工阶段，还是长期运营阶段，需十分关注隧道纵向轴力变化。建议在抗扭设计中充分考虑纵向轴力对隧道抗扭的影响，并采取螺栓预紧或预应力管片结构等措施[27]。

图14 等效抗扭刚度有效率与压扭比的关系Fig.14 Relationship between longitudinal torsional stiffness efficiency and compression-torque ratio

3.5 弯扭比

图15 所示为弯扭组合状态下弯扭比对隧道等效抗扭刚度以及扭转中心位置的影响曲线图。从图15 可以看出：当弯扭比M/T小于临界比(M/T)cr即16.7 时，隧道纵向等效抗扭刚度与弯扭比呈非线性的正相关关系，且曲率随着弯扭比增大而增大，特别是当M/T＞8 时，等效抗扭刚度有效率提升速率极大；当M/T＞(M/T)cr时，抗扭刚度有效率为100%。这说明隧道的抗扭性能对纵向弯矩十分敏感。纵向弯矩往往随着隧道不均匀沉降的产生而出现，由此引起的附加内弯矩在一定程度上能提升隧道的抗扭性能。从图15 可进一步得到：当M/T＜(M/T)cr时，扭转中心距隧道中心的距离与弯扭比呈非线性的正相关关系，且曲率随着弯扭比增大而减小；当M/T＞6 时，基本可认为环缝扭转中心位置即在纯弯状态下的扭转中心处。

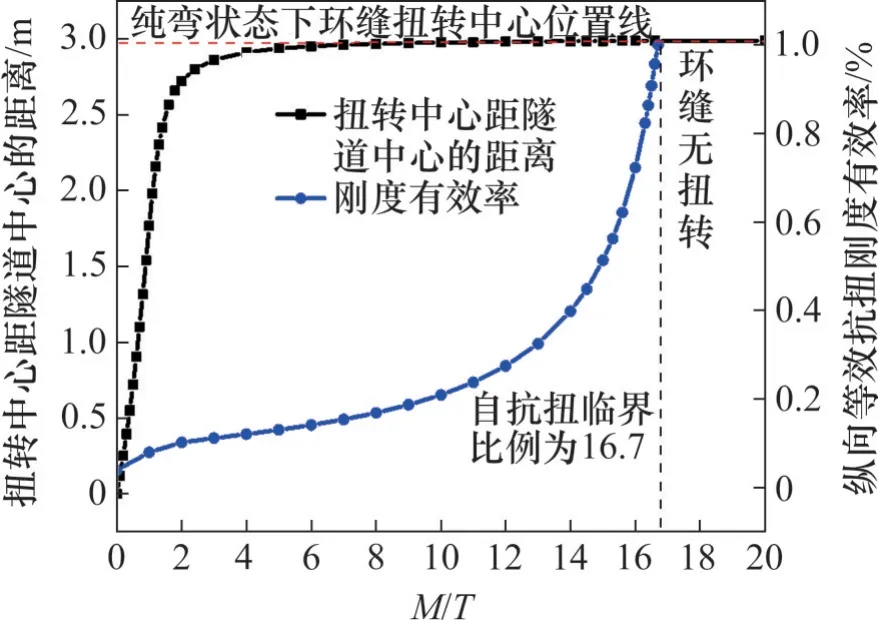
图15 隧道纵向抗扭性能与弯扭比的关系Fig.15 Relationship between longitudinal torsional performance and bending-torque ratio

4 结论

1) 提出了不同受力组合状态下的盾构隧道纵向等效抗扭刚度解析解，利用数值模型验证了解析解的有效性。

2) 管片和螺栓尺寸对盾构隧道抗扭性能影响显著。隧道纵向抗扭刚度有效率随着管片厚度与直径比增大而减小，而随着管片环宽与直径比增大而增大。盾构隧道纵向抗扭刚度有效率随着螺栓的等效剪切长度增大而减小。此外，螺栓等效剪切长度仅影响环缝的扭转变形，而对接缝中性轴、扭转中心位置等没有影响。

3) 隧道抗扭性能对纵向轴力和弯矩的变化十分敏感。盾构隧道纵向抗扭刚度有效率随着压扭比或弯扭比增大而增大。当压扭比达到临界比0.58或弯扭比达到16.7 时，刚度有效率将达到上限即100%。而当纵向轴力和弯矩降为零时，抗扭刚度有效率达到下限，约为4%。因此，控制合理的压扭比与弯扭比对隧道抗扭设计十分重要。可将增大螺栓预紧力或采用预应力管片结构视为提升盾构隧道抗扭性能的有效措施。

4) 本模型仅考虑弹性状态下直螺栓和接缝摩擦提供的抗扭矩。因此，对于弹塑性状态下带有剪力键或者凹凸榫的隧道结构扭转模型，还需要进一步研究与验证。此外，关于螺栓有效剪切长度系数λ还需通过室内实验或现场监测等予以验证。