基于随机场理论的顶管隧道施工地表变形特性分析
张轩煜,施成华,孙晓贺,彭立敏,郑可跃,王祖贤,肖国庆
(中南大学 土木工程学院,湖南 长沙,410075)
随着城市地下交通快速发展,顶管法在地下交通建设中的应用逐渐增多。但顶管顶进对周围土体存在扰动[1-2],导致周围地层应力场变化及土体变形,进而引起地表变形,严重影响周边建筑物及地表交通的安全,因此,分析和预测顶管隧道施工引起的地表变形具有重要意义。目前在顶管施工引发地表变形的研究中,主要方法有经验公式法[3]、理论解析法[4]和数值分析法[5]。PECK[6]根据工程经验提出了沉降槽呈近似正态分布的PECK公式,在工程实际中得到了广泛应用;蒋凯等[7]采用普式压力拱理论与土柱理论分析了长距离曲线顶管隧道施工中的力学行为;喻军等[8]通过建立顶管施工数值模型,考虑施工参数的影响,分析了地表变形影响规律。这些方法通常将周围地层土体视为均质材料,但实际上岩土体并非严格均质,在同一地层中,不同位置的土体物理力学性质存在不同程度的偏差,2种土体的物理力学性质偏差呈一定的相关性,即岩土体具有空间变异性和自相关性的特点[9]。为体现岩土体的这一特性,可采用随机场理论进行研究。随机场理论能够将地层参数随机化,通过土体参数的均值、方差、变异系数和相关距离表征土体空间变异性和自相关性,分析其对顶管施工地表变形的影响,因此,有必要采用随机场理论研究顶管施工引发的地表变形。
既有研究在使用随机场理论分析工程问题时,通常建立二维模型进行模拟分析。赵炼恒等[10]通过随机场理论建立二维模型,分析了土体的空间变异性对分层边坡的可靠度的影响;易顺等[11]针对基坑开挖引起地表变形的问题,采用随机场理论建立平面数值模型,研究了土体参数的空间变异性对基坑变形规律的影响;程红战等[12]采用随机场理论建立二维模型,研究了地层土体的空间变异性对盾构施工所引发的地表变形的影响及规律。然而,二维随机场无法描述岩土体在3个方向上的空间变异性和自相关性[9],同时,顶管顶进过程是三维动态过程,二维随机场模型不能体现顶管施工顶进过程对地表纵向变形的影响,因此,有必要基于三维随机场理论充分考虑地层参数在各个方向上的空间变异性和自相关性,建立模拟施工顶进过程的三维顶管模型,研究顶管施工对地表变形的影响。
本文基于随机场理论,通过有限元分析软件建立模拟施工顶进过程的三维顶管模型,在此基础上,采用高斯型自相关函数、KL级数展开法的随机模拟方法对模型中的地层参数进行随机性分析,揭示顶管顶进施工引发的地表随机变形特性,分析地层参数、变异系数以及相关距离对地表变形的影响,提出考虑地层空间变异性的简化计算方法。
1 随机场基本原理及三维随机场的实现
1.1 随机场概述
随机场理论最早由VAN MARCKE提出[13],目前已被广泛用于表征地层土体的空间变异性和自相关性[14],这种特性在地层土体中表现为物理力学参数具有波动范围,服从概率分布,并与邻近土体存在关联。随机场理论可以很好地描述这一特性,并将同一地层中同一物理力学参数的随机变量定义为一个随机场[15-16]。
假定存在n个数据点(x1,x2,…,xn),并定义K为这些数据点的协方差矩阵,则矩阵K对称且正定,由此可将K进行Cholesky分解。
式中:L和U分别表示上三角矩阵和下三角矩阵;角标T 表示矩阵的转置。定义随机向量y=Lv,其中,v为服从标准正态分布N(0,1)的随机向量,则yyT(N阶方阵)的期望值由下式得到:
由于v为服从N(0,1)分布的随机向量,故
其中,I为单位矩阵。通过协方差矩阵K求得随机向量y,再根据物理力学参数具体值即可求出点x1,x2,…,xn处的随机模拟值。
为得到协方差矩阵K,需确定合适的自相关函数,以描述地层中任意两单元之间的相关性[17],同时,随机场理论上可以离散为无限个单元点。为了减小计算量并控制精度,需选择合适的离散方法将随机场离散为n个数据点。
1.2 自相关函数
采用随机场理论建立模型,需使用自相关函数确定随机模型中任意2点之间的相关性。在既有二维随机场的研究中[11-12],计算土体相关性时,只考虑了2个方向的相关性,存在一定的局限性。三维随机模拟方法考虑了土体3个方向(x、y、z)的相关性,能够更好地模拟地层土体在空间上的变异性。
由于高斯型自相关函数具有良好的连续性和平顺性,因此,选用高斯型自相关函数表征地层中任意两土体之间的相关性大小,其表达式[18]如下:
式中:ρ(τx,τy,τz)表示地层中2 点之间的相关性;τx、τy、τz分别表示地层中2点在x、y和z3个方向上的距离;sx、sy、sz分别表示地层中2 点在x、y和z3个方向上的相关距离。随机场中任意2个单元的相关性只取决于它们之间的距离。假设将1个随机场离散为n个随机场单元,每个单元中心坐标为 (xi,yi,zi),则整个随机场中所有单元之间的自相关系数将组成如式(6)所示协方差矩阵:
式中:τx12表示点1 与点2 在x方向上的距离,因此,τx12=τx21,ρ(τx12,τy12,τz12)=ρ(τx21,τy21,τz21),协方差矩阵是元素为1的对称矩阵。
1.3 基于KL级数展开法的随机场离散
目前,随机场离散的方法较多,其中,KL 展开法具有精度和效率均高的优点[18-20],因此,采用KL展开对随机模型进行离散。
1.3.1 KL级数展开公式
首先将研究对象离散为一组独立标准正态随机变量[19],即
式中:xi为需要进行离散的地层参数;xi(x,y,z)为随机场xi的均值;ΔHxi(x,y,z;θ)为随机场xi的波动部分,其本质是具有原随机场相关特性的一个零均值随机场;δXi为随机场xi的均方差;M为随机场的级数展开项数;λj和fj(x)分别为H(x,y,z;θ)的特征值和特征函数。
1.3.2 特征值和特征向量的求解
为确定相关函数的特征值λj和特征函数fj(x),采用Fredholm二类积分方程对展开的ΔHxi(x,y,z;θ)的协方差函数C(x1,y1,z1;;x2,y2,z2)求解,如式(8)所示[21-22]:
式中:Ω为积分区域。
1.3.3 级数展开项数的确定
随机场的离散理论上可以进行无穷多项展开,但为了减小工作量并保证计算精度,通常需确定级数展开过程中的截断项数n。对此,通过以下方法[23]求解随机场的离散误差ε:
式中:N为随机场模型离散后的单元数目;ε(xj)为离散后单元xj的均方误差。
1.4 三维随机场的实现
既有研究在使用二维随机场分析工程问题时,只考虑了2个方向上的空间变异性。为表征地层土体空间变异性在三维空间上对顶管施工地表变形的影响,考虑3个方向的空间变异性,建立三维随机场模型分析工程问题。
图1所示为随机场理论的实现流程。通过地勘报告获取各地层物理力学参数的均值、方差、变异系数和相关距离,根据均值建立模拟施工顶进过程的三维顶管模型,对确定参数的模型进行分析,得到确定性分析结果。同时,根据均值、方差、变异系数和相关距离,选择合适的自相关函数,生成表征同一地层中各土体之间相关性的协方差矩阵,并通过地层土体的均值和变异系数,利用KL 级数展开法对随机场进行n项展开,最终得到该地层土体的随机参数。将生成的随机参数赋予确定性分析模型中的单元,生成地层土体具有空间变异性和自相关性的随机性分析模型,即可通过计算得到随机模型不同顶进阶段的横向和纵向变形,进一步分析顶管顶进过程和土体随机性对地表变形的影响规律。
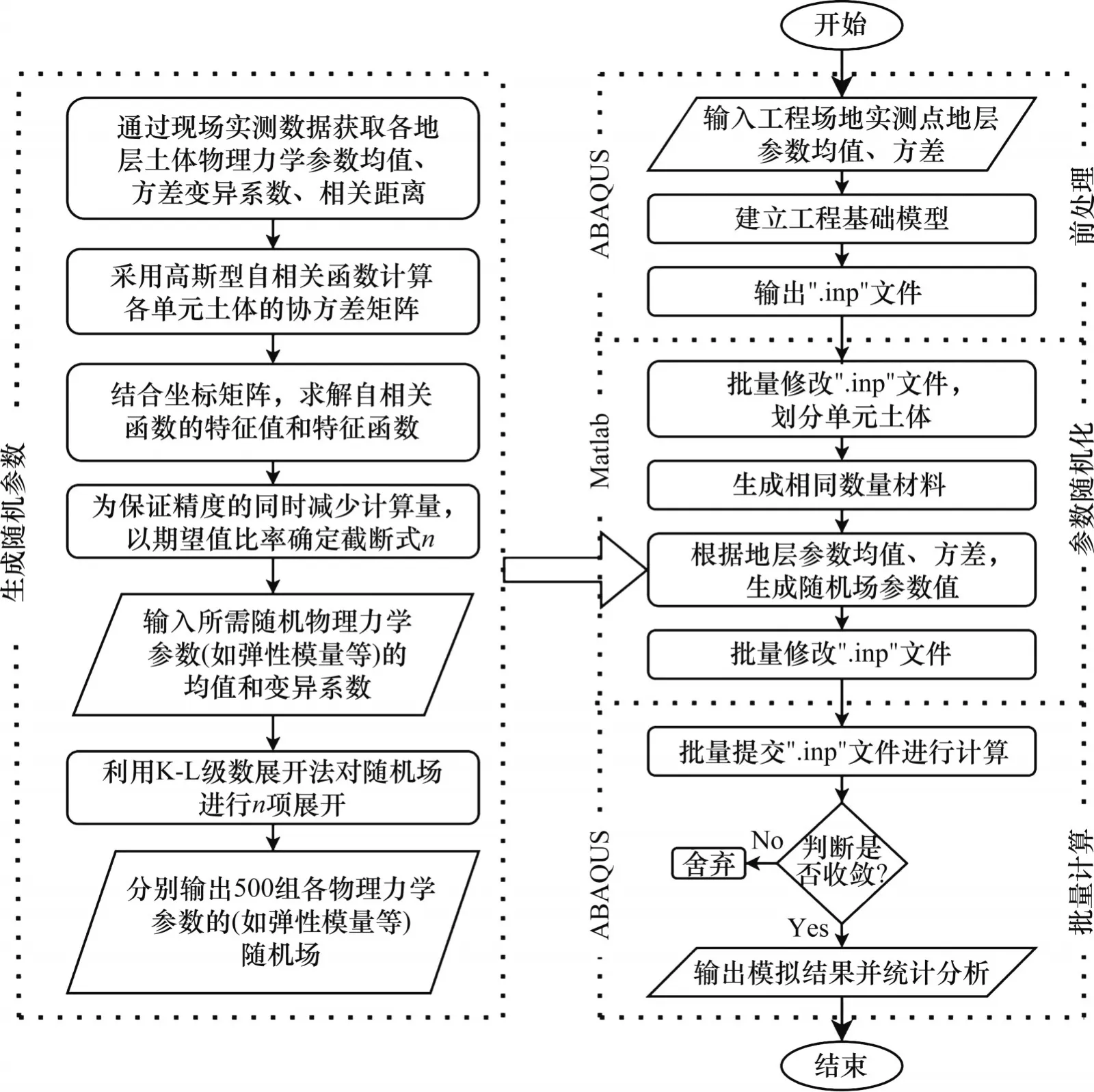
图1 随机场理论实现流程Fig.1 Implementation processes of random field theory
2 基于三维随机场的顶管案例分析
为验证随机模拟方法用于研究顶管施工地表变形的适用性以及相比于确定性分析的优越性,以南宁市地铁1号线金湖广场站Ⅲ号出入口顶管工程[24]为例,采用有限元软件建立顶管隧道施工三维有限元模型。通过随机场理论各生成500组[11]地层参数,计算随机模型地表沉降并评估地表变形超标概率,验证随机场理论的可靠性。
2.1 工程概况
该工程采用土压平衡多刀盘顶管机施工,顶进长度为37.2 m,管节覆土厚度约为5 m,管节外轮廓长×宽为6.9 m×4.9 m,厚度为0.5 m,管节长度为1.5 m,南宁地铁1 号线金湖广场站Ⅲ号出入口概况如图2所示。
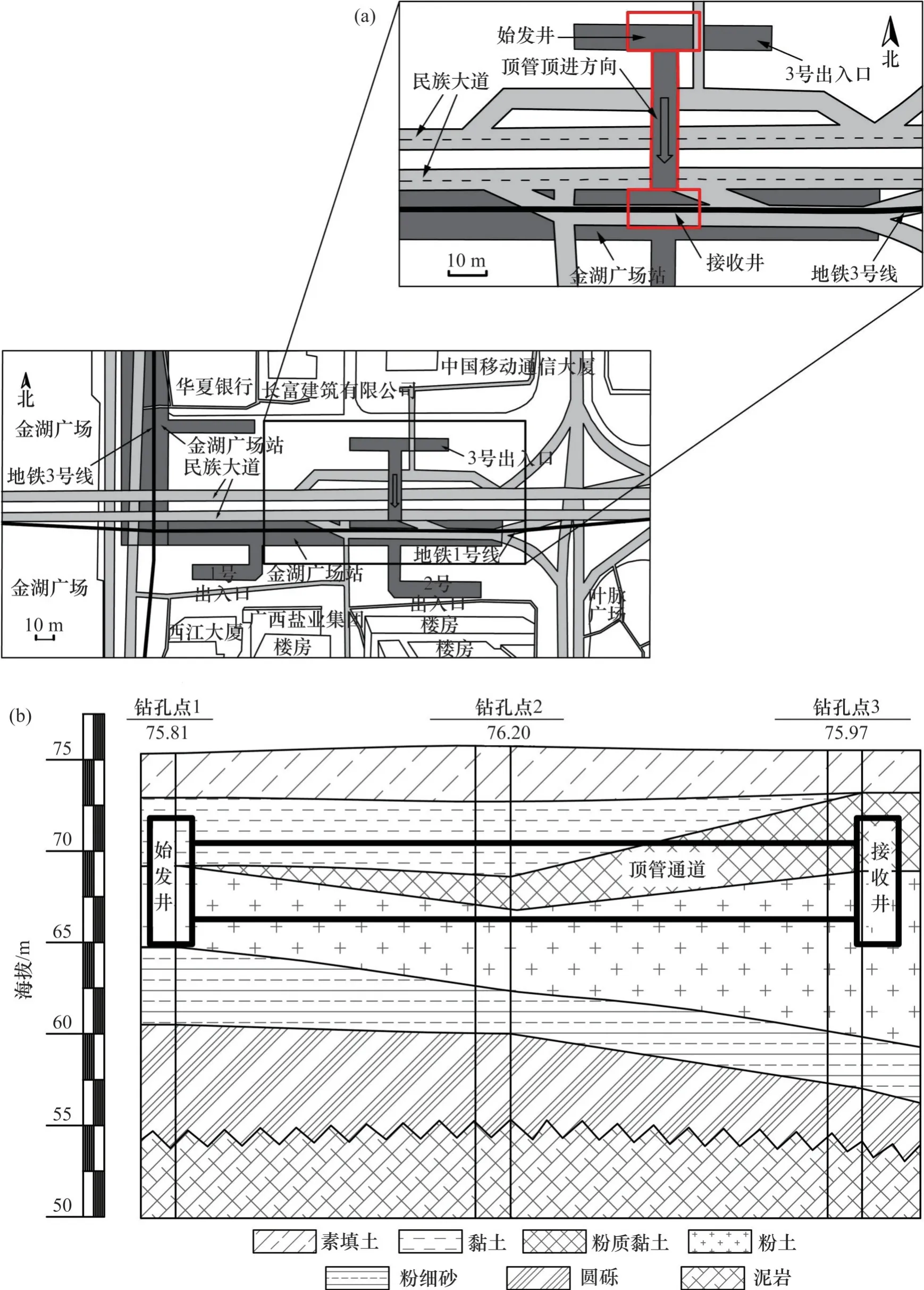
图2 南宁地铁1号线金湖广场站Ⅲ号出入口概况Fig.2 Entrance III overview of Nanning metro line 1 in Jinhu Square Station
2.2 模型假设和建立
2.2.1 确定性分析模型的建立
为便于模型建立和分析,在建模时将地层简化为均匀厚度的土体。假设土体是密实均质的弹塑性材料,采用Mohr-Coulomb本构模型,地层损失沿顶进方向均匀分布,在顶管顶进过程中不考虑顶管的缓慢推进,每次顶进距离为管节的长度。在顶进过程中,顶进面设置均布荷载模拟顶推力,且在顶进过程中保持不变。图3(a)所示为该顶管工程的三维有限元数值模型,由7个地层组成,设置模型侧面边界为法向约束,模型底面为3个方向的固定约束,上表面为自由面不设置约束。管节采用弹性本构模型,各地层土及管节物理力学参数如表1所示。
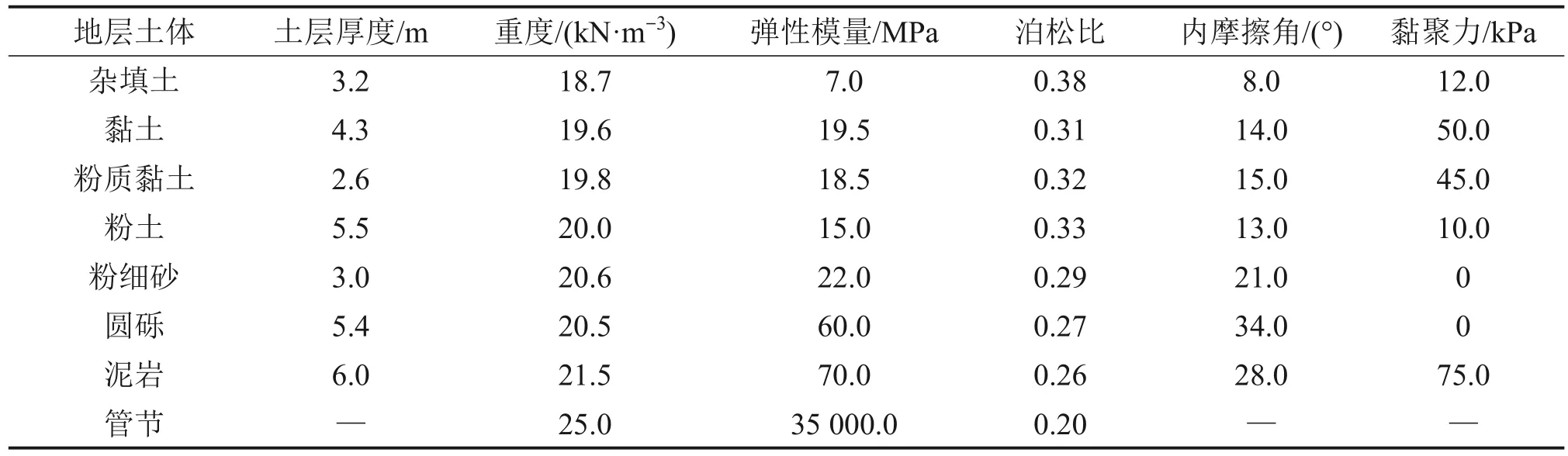
表1 各地层土及管节物理力学参数Table 1 Physical and mechanical parameters of soil and pipe joints in each stratum
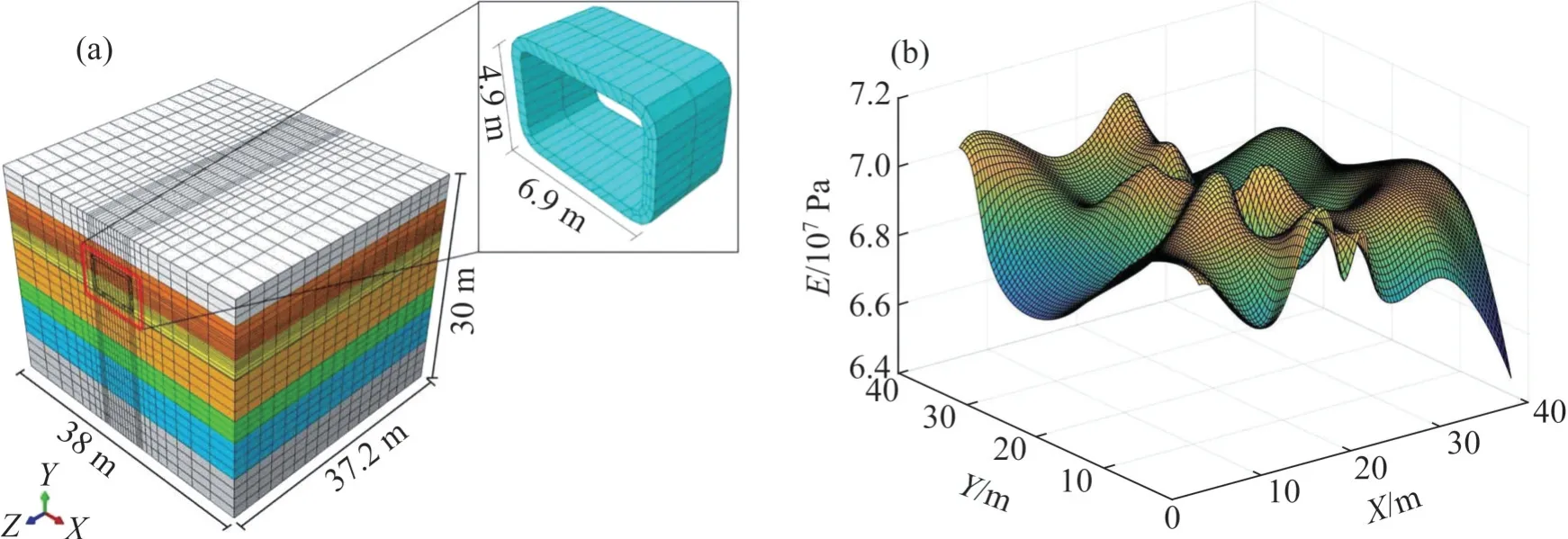
图3 三维有限元数值模型Fig.3 3D finite element numerical model
2.2.2 随机性分析模型的建立
为验证随机场理论分析顶管施工中地表变形的可靠性,根据上述随机场理论,拟定对地层单元土体的天然密度、内摩擦角、黏聚力和弹性模量进行随机化,同时,根据工程实际地层土体属性,取水平相关距离为10 m,竖直相关距离为2 m[25-27],地层土体参数中重度、黏聚力、内摩擦角和弹性模量的变异系数分别为0.02、0.10、0.10和0.30[28],并生成500组随机场进行分析。为体现随机性分析中单元土体参数的变化规律特征,以泥岩地层中单元土体的弹性模量(E)为例说明各地层土体所存在的空间变异性,如图3(b)所示(其余地层单元土体的各物理力学参数也表现出类似规律)。
2.3 三维随机场分析
顶管施工段地表沉降现场监测点布置如图4所示。通过数值模拟得到三维沉降模型,并对此进行横向沉降和纵向沉降分析,其地表沉降示意图及纵向、横向分析截面如图5所示。

图4 顶管施工段监测点布置图Fig.4 Monitoring point layout of pipe jacking construction section

图5 确定性分析地表沉降及分析截面Fig.5 Deterministic analysis surface of settlement and cross sections for analysis
2.3.1 纵向分析
图6所示为顶管顶进到不同位置时的纵向地表沉降。从图6可以看出:确定性分析曲线与随机性分析曲线的变化规律一致,随机沉降曲线在确定性分析沉降曲线附近波动,确定性分析曲线基本位于随机曲线中间位置。通过比较不同顶进距离下的地表沉降曲线可知:各横断面的地表沉降范围随着顶管的顶进逐渐增大,并在顶管顶进完成后沉降不变。以距始发井0 m的横断面为例,当顶管顶进5 m 时,其地表沉降的随机范围为-19.8~-6.7 mm;随着顶管的逐步顶进,其确定性分析的沉降有所增大,随机性分析结果的沉降和包络范围相应增大;当顶管顶进完成时,该断面的随机沉降范围达-29.3~-19.8 mm;随着顶管的逐步顶进,各断面地表沉降和随机沉降曲线的主要包络范围逐渐增大。由此可见,地层参数的空间变异性对顶管施工引发的地表变形产生较大影响。
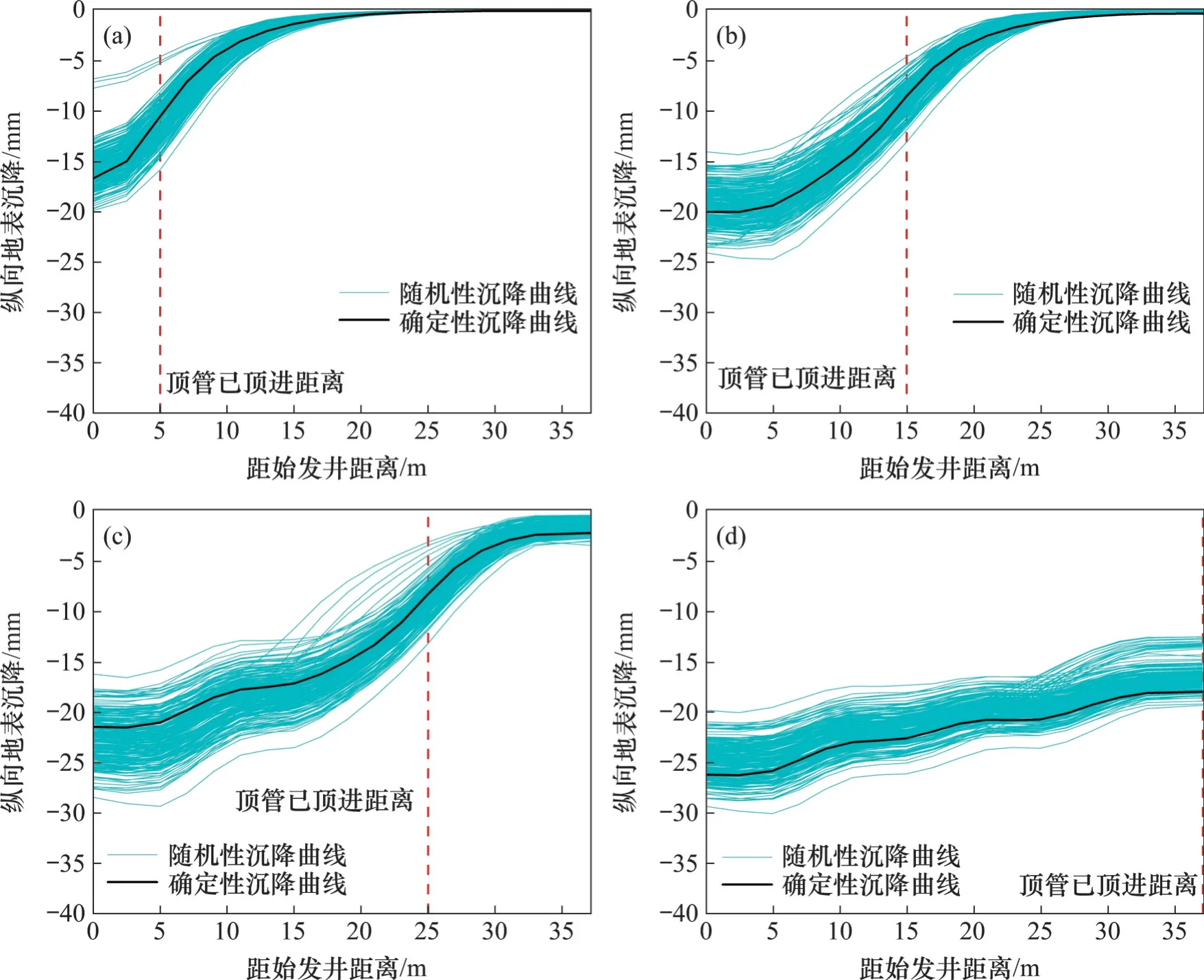
图6 随机性纵向地表沉降Fig.6 Stochastic longitudinal surface settlement analysis
在不同的顶进距离下,地表变形形态均不同;当顶管开始顶进时,顶进面前方一定范围内的土体会发生不同程度的地表沉降,且距离顶进面越远,地表沉降越小。随着顶管的顶进,地表变形向顶进方向延伸,未顶进段开始产生地表沉降,已顶进段的地表沉降变化较小,并在顶管顶进完成后地表沉降不变。如顶管顶进5.0 m时,距离始发井0~21.0 m 的纵向范围内均出现地表沉降,最大沉降为-19.8 mm;顶进15.0 m时,纵向0~27.0 m的范围内出现了地表沉降,最大沉降为-24.7 mm。
2.3.2 横向分析
图7所示为顶进完成后各监测断面的监测点沉降和确定性分析、随机性分析结果,表2所示为顶管顶进完成后各监测断面确定性分析、随机性分析的各监测断面沉降模拟值和监测点监测值。从图7和表2可以看出:确定性分析和随机性分析所得出的地表沉降趋势与监测的沉降趋势较符合,但由于模型建立时受地层的简化等因素的影响,确定性分析所得沉降与断面监测值在最大变形处存在差异。随机性分析在确定性分析的基础上,给出了地表变形的范围,能够将监测值较好地包络,可对地表变形进行较好预测。如对于监测断面A,其监测点沉降变化趋势与确定性分析和随机性分析的沉降曲线变化趋势一致,确定性分析和随机性分析所得到沉降的最大沉降基本位于顶管中轴线附近,监测值为23.8 mm,确定性分析最大沉降为-26.4 mm,随机沉降曲线的包络范围为-33.1~-17.3 mm,确定性分析所得到结果与监测结果存在一定的差距;随机性分析所得到的包络范围能够将监测值包络,较好地预测顶管施工中的地表变形。

表2 顶管顶进完成后各监测断面沉降Table 2 Settlements of each monitoring section after completion of pipe jacking mm
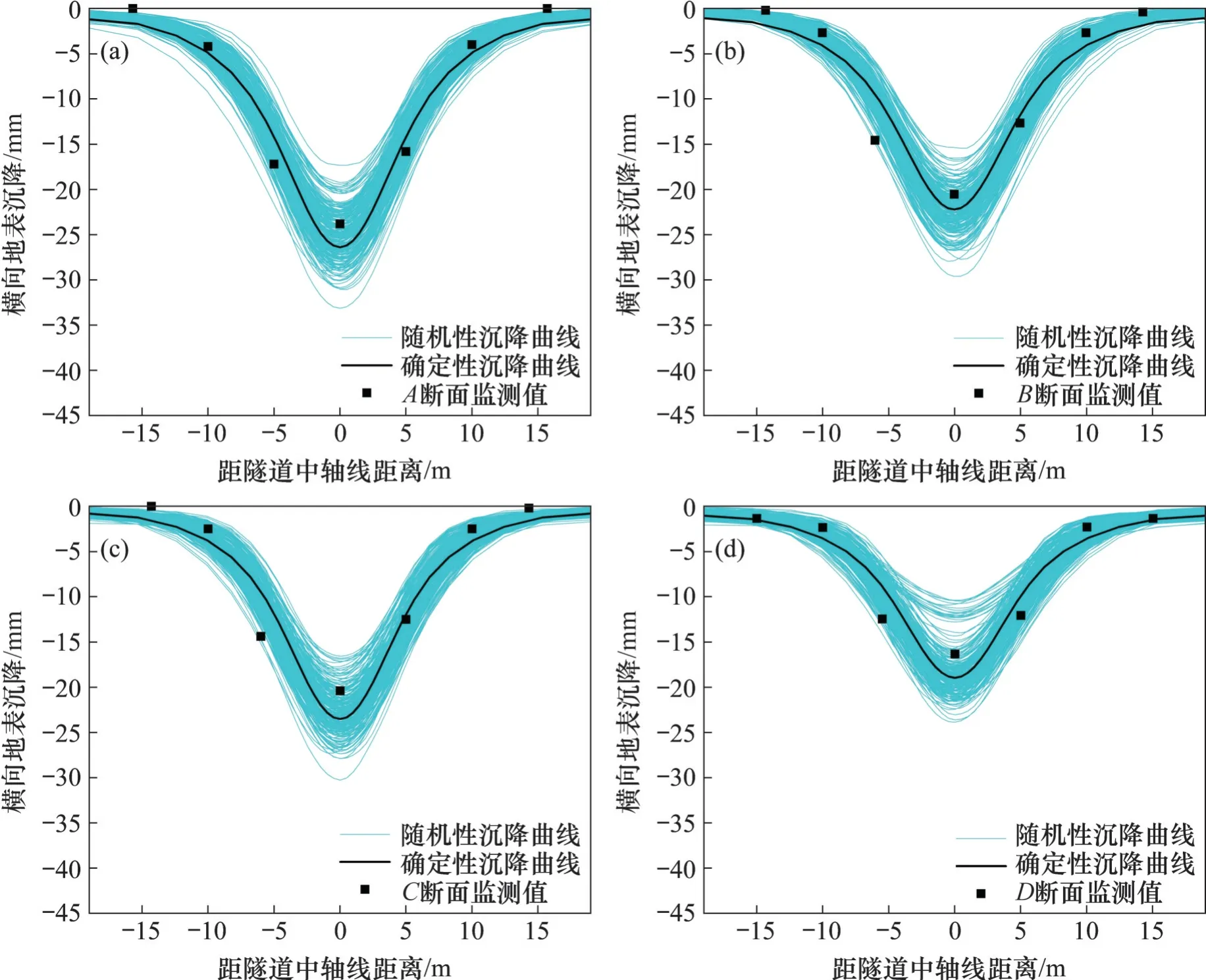
图7 横断面沉降随机性分析结果Fig.7 Cross-sectional settlement randomness analysis results
2.4 三维随机场超出变形控制值概率分析
相比于二维随机场,三维随机场考虑了3个维度的空间变异性和顶管施工的顶进过程,对此分别从纵向和横向分析地层参数空间变异性对地表变形的影响。为进一步量化施工过程中地表变形超出控制值的概率,通过式(11)[12]计算超出控制值的概率P:
式中:N为每个工况中随机计算的次数(N=500);Nf为计算结果大于最大沉降控制值的次数。
对顶管顶进过程中各监测断面地表变形的超标概率进行计算,计算结果如图8 所示。从图8可以看出:根据顶管顶进过程中各断面地表沉降控制值,可得到其可能超出控制值的概率;以顶管顶进到25 m 为例,当监测断面A的控制值为-20 mm 时,其失效概率高达90%,当控制值为-25 mm 时,失效概率为13%;对于横断面C,沉降控制值7.5 mm 所对应的失效概率为91%,控制值-11 mm 所对应的失效概率为18%。由此可在施工顶进过程中,预测各监测断面地表沉降超出控制值的概率。
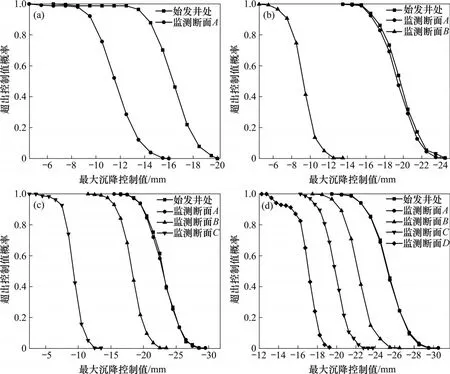
图8 地表沉降超标概率分析结果Fig.8 Analysis results of probability of surface settlement exceedance
3 顶管隧道地层参数空间变异性的影响分析
为分析不同地层参数随机化对顶管施工中地表变形的影响,在上述案例确定性分析模型的基础上,分别对地层土体参数(弹性模量、内摩擦角、黏聚力)、相关距离和变异系数单独随机化,对比分析各因素对地表变形的影响。随机性分析参数如表3所示[11,29-30]。为便于比较各地层参数随机化对地表变形的影响,取顶进完成后B测点横断面地表沉降进行比较分析。
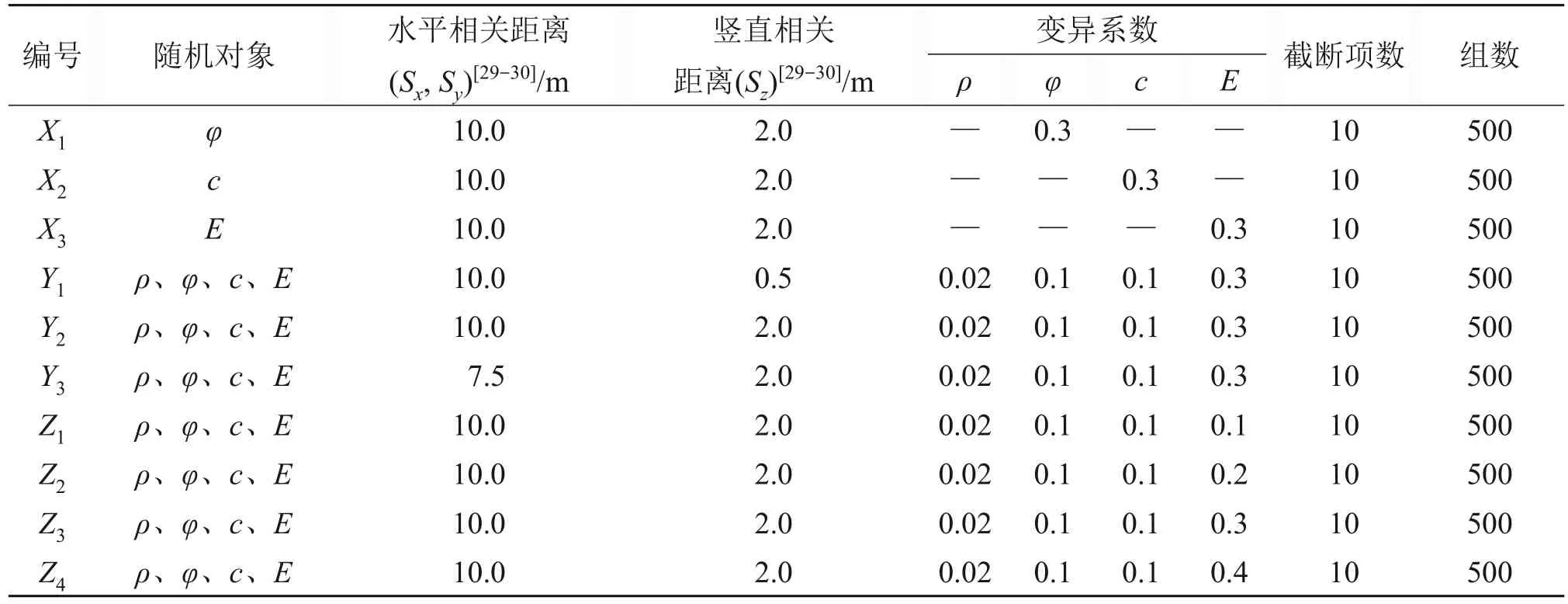
表3 随机性分析参数[11, 29-30]Table 3 Parameters of randomness analysis
3.1 地层土体参数不确定性的影响
图9 和图10 所示分别为地层土体内摩擦角、黏聚力和弹性模量随机化下顶管施工地表沉降曲线和地表水平位移曲线。从图9和图10可以看出:确定性分析曲线基本位于随机沉降范围的中间位置,随机沉降曲线在确定性沉降曲线附近波动,其沉降变化规律与确定性曲线变化规律相符;在相同变异系数下,弹性模量的随机化对地表变形有较大影响,能够使随机曲线更加离散,随机曲线所包络的范围更广,其随机沉降包络范围达-25.9~-16.1 mm;黏聚力和内摩擦角对地表变形的影响相对较小,其随机沉降包络范围分别为-25.1~-19.6 mm 和-23.8~-17.6 mm;地层土体物理力学参数的随机化不会改变地表变形的变化规律和变化趋势。由于工程实际中土体重度的变异性较低,其变异系数相比于弹性模量的变异系数要小很多,地表横向离散曲线与沉降曲线基本一致。由此可知,土体物理力学参数中弹性模量的不确定性对顶管施工地表沉降的影响最大,其次是内摩擦角和黏聚力,且这两者影响程度相近。
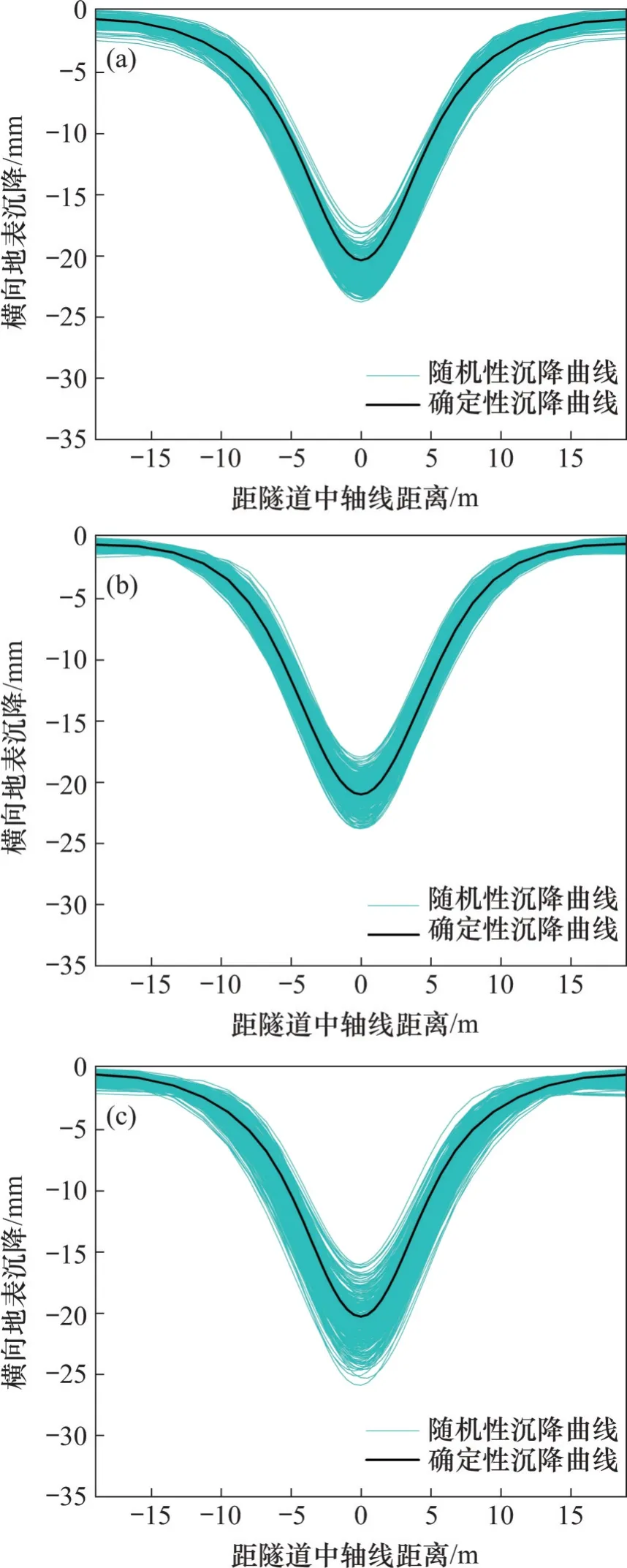
图9 土体物理力学参数不确定性分析所得横向地表沉降曲线Fig.9 Soil transverse surface settlement curves based on uncertainty analysis of physical and mechanical parameters
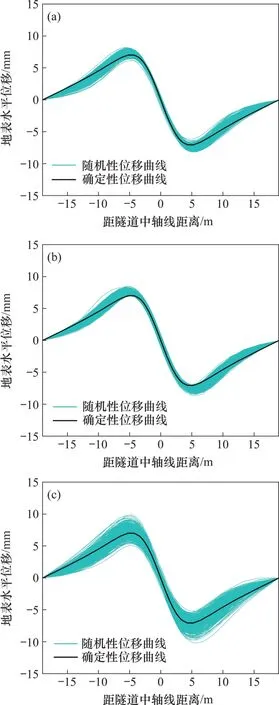
图10 土体物理力学参数不确定性分析所得地表水平位移曲线Fig.10 Surface horizontal displacement curves based on uncertainty analysis of physical and mechanical parameters of soil
3.2 相关距离的影响
图11 所示为地层参数在不同相关距离下的地表沉降曲线,图12 所示为不同相关距离下的地表水平位移曲线。从图11和图12可以看出:相关距离对地表变形的离散程度存在一定的影响,当Sx=Sy=10,Sz=2 时,随机沉降曲线的随机范围最大,为-28.9~-14.1 mm;随着水平或竖直相关距离减小,随机沉降曲线的沉降范围有所减小。这是由于相关距离减小,地层中土体的相关性减弱,物理力学参数的离散性增大,导致随机计算结果更加离散。不同相关距离也会在一定程度上改变地表变形的形态,这是由于相关距离的改变会使得地层土体出现整体均质、局部异质的特点,进而导致地表变形曲线不对称。因此,相关距离对地表变形的影响不可忽视,相关距离越大,对地表变形的影响越大。
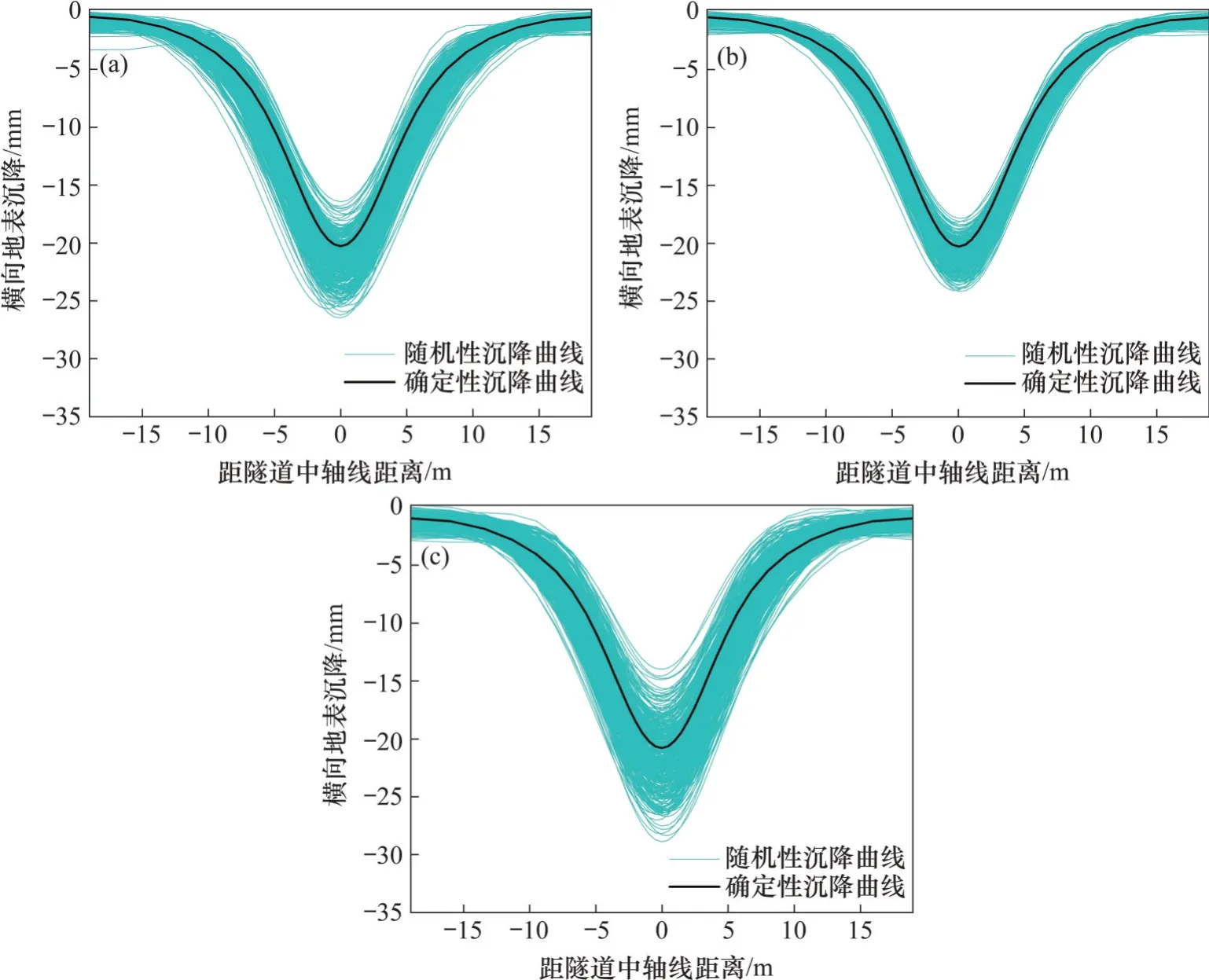
图11 不同相关距离下横向地表沉降曲线Fig.11 Transverse surface settlement curves at different correlation distances
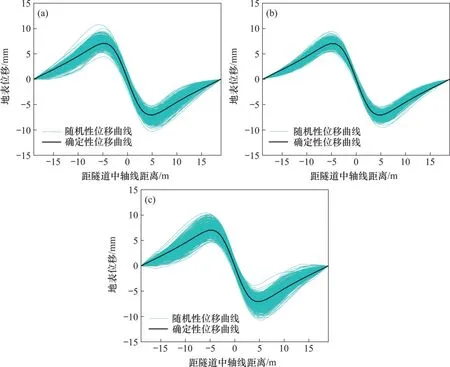
图12 不同相关距离下地表水平位移曲线Fig.12 Surface horizontal displacement curves at different correlation distances
3.3 变异系数的影响
地层参数的空间变异性通过变异系数予以表征。图13 所示为不同变异系数对地表沉降曲线的影响,图14 所示为不同变异系数下地表水平位移曲线。从图13和图14可以看出:变异系数不会改变既有的地表变形规律和趋势,其对地表变形的影响主要表现为随机曲线离散程度不同;当变异系数为0.1时,随机性分析的变化趋势与确定性分析一致,沉降曲线相对集中,最大沉降为-24.4~-18.7 mm,变化范围较小;随着变异系数增大,地表沉降趋势与确定性分析结果无明显差别,但曲线分布更加离散;当变异系数为0.4时,地表最大沉降为-27.1~-14.0 mm。这是由于变异系数增大,地层参数的不均匀性增加,使得计算得到的地表变形结果更加离散,因此,变异系数越大,地表变形结果更加离散。不同变异参数下的地表最大沉降统计如图15所示。
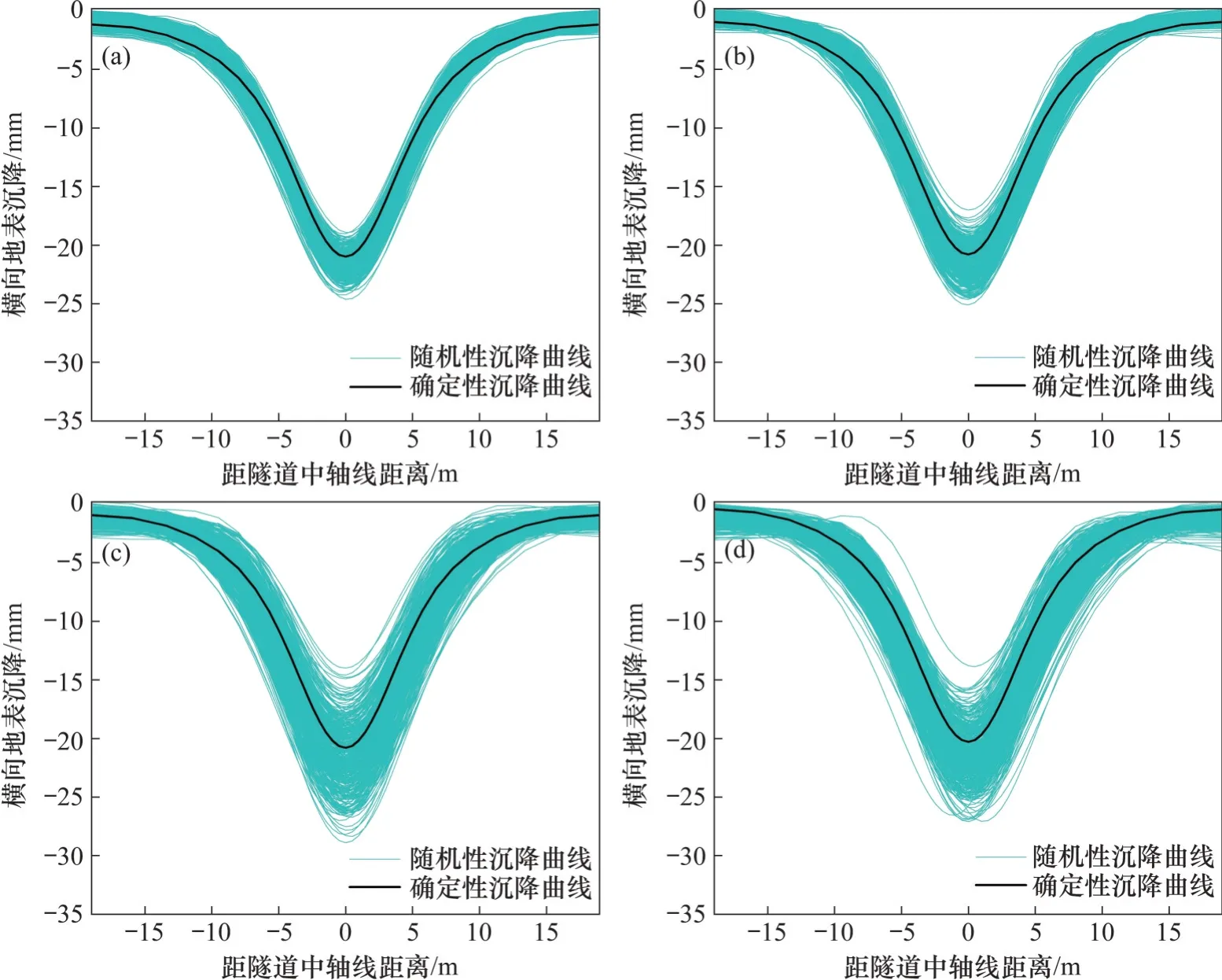
图13 不同变异系数下横向地表沉降曲线Fig.13 Transverse surface settlement curves under different coefficients of variation
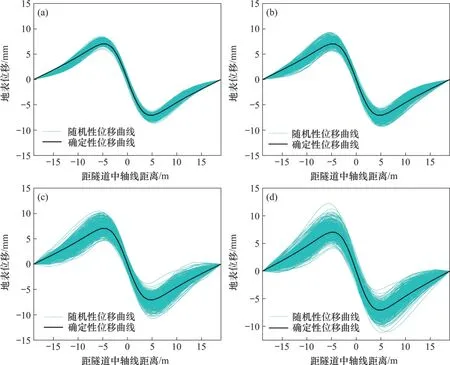
图14 不同变异系数下地表水平位移曲线Fig.14 Surface horizontal displacement curves under different coefficients of variation
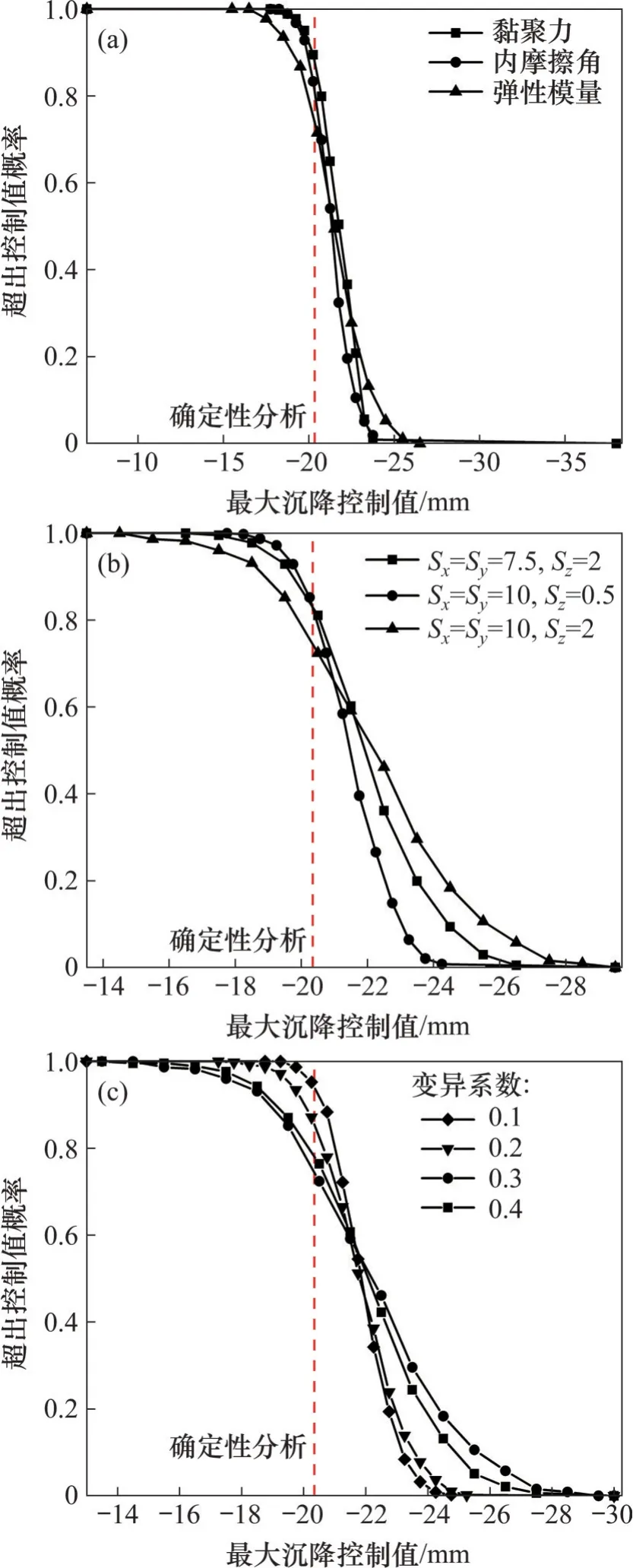
图15 不同变异参数下地表最大沉降统计Fig.15 Statistics of the maximum surface sedimentation with different coefficients of variation
4 结论
1) 基于高斯型自相关函数、KL级数展开法的三维随机模拟方法能够有效表征地层参数变异性和自相关性,得到顶管施工所引起的地表纵、横向变形特性,反映地表变形规律和变形范围的影响。
2) 相比于确定性分析方法,随机性分析所得结果能够充分表征顶管施工所引发地表变形的趋势、数值和波动范围,更加贴合工程实际中较复杂的情况,所得结果较确定性分析结果更具有借鉴作用和参考价值。
3) 与二维随机分析结果相比,三维随机分析考虑了地层中3个维度的空间变异性以及顶管施工的动态影响,可从纵向和横向2个角度分析不同顶进距离下各纵断面和横断面的地表变形,并能得出地表变形超标概率。
4) 弹性模量的空间变异性对地表变形随机曲线的离散程度和变形范围有较大影响,但不改变变形的变化趋势和规律;变异系数和相关距离增大能够使得地表变形随机曲线更加离散。

