木材横向切断性能螺旋管胞模拟研究
殷鑫 孟兆新 宋绪秋 乔际冰 王猛


摘 要:为进一步了解木材横向切断性能,优化木材的加工流程,减少资源浪费,以木材管胞理论为基础,提出一种木材螺旋管胞结构模型,并在建模和砌体代表性体积单元(Representative Volume Element, RVE)均质化后在Abaqus/Explicit中进行横向切断仿真研究。研究选取挪威云杉(Picea abies)作为试验材料,基于螺旋管胞结构进行建模,设定模型属性、边界条件、划分网格并装配后进行仿真及后处理,导出相关数据,与常规结构模型仿真结果和实际试验结果进行对比研究。结果表明,基于螺旋管胞结构的模型仿真结果相较于常规结构模型仿真结果更接近实际试验结果,为日后木材仿真研究和木材加工优化提供了有利的参考依据。
关键词:木材切断;螺旋管胞结构;均质化;有限元;数值模拟
中图分类号:S781.21 文献标识码:A 文章编号:1006-8023(2023)04-0086-7
Helical Tracheid Simulation Study of Wood Transverse Cutting Performance
YIN Xin, MENG Zhaoxin*, SONG Xuqiu, QIAO Jibing, WANG Meng
(College of Mechanical and Electrical Engineering, Northeast Forestry University, Harbin 150040, China)
Abstract:In order to further understand wood transverse cutting performance, optimize wood processing process and reduce resource waste, based on wood tracheid theory, this paper proposed a model of wood helical tracheid structure, and carries out transverse cutting simulation study in Abaqus/Explicit after modeling and representative volume element (RVE) uniformity. Picea abies was selected as the test material to conduct modeling based on the helical tracheid structure. Model attributes, boundary conditions, mesh division and assembly were set for simulation and post-processing. Relevant data were derived and compared with the conventional structural model simulation results and actual experimental results. The results showed that the simulation results based on helical tracheid structure were closer to the actual experimental results than the conventional structural model simulation results, which provided a favorable reference for future wood simulation research and wood processing optimization.
Keywords:Wood cutting; helical tracheid structure; homogenization; finite element; numerical simulation
收稿日期:2022-10-21
基金項目:中央高校基本科研业务费专项(2572018CP08)
第一作者简介:殷鑫,硕士研究生。研究方向为木材断裂仿真。E-mail: 330168992@qq.com
通信作者:孟兆新,博士,教授。研究方向为机械系统仿真、机电控制技术、农林业创新设计等。E-mail: mzhxmail@163.com
引文格式:殷鑫,孟兆新,宋绪秋,等. 木材横向切断性能螺旋管胞模拟研究[J]. 森林工程,2023,39(4):86-92.
YIN X, MENG Z X, SONG X Q, et al. Helical tracheid simulation study of wood transverse cutting performance[J]. Forest Engineering, 2023, 39(4):86-92.
0 引言
木材作为应用最广泛的材料之一,在四大材料(钢材、水泥、木材、塑料)中,是唯一可再生、可循环利用、可自然降解的绿色材料和生物资源[1]。木材工业中,木材的机械加工质量本身便是成品的附加值,对加工质量的改进即是对产品价值的提高。木材的加工工艺受到多种因素的影响,其中木材的结构、力学性质等占据了很大一部分,对木材的切断过程进行更深入的分析,能更精准地计算能量消耗,帮助优化木材的加工流程。
国内外对木材的研究众多。Khelifa等[2]针对木材切割断裂过程提出一种基于连续损伤和各向异性塑性理论的增量方法,并使用有限元软件进行了验证;Lukacevic等[3]提出了一个基于木材微观结构的多表面破坏准则表明脆性和韧性的破坏机制,并构建一种新的算法在数值模拟中,同时描述塑性破坏和开裂;Salmén[4]讨论了细胞壁的复杂性,描述了基于不同细胞壁结构对其特性进行建模的能力;Carlsson等[5]采用高分辨率有限元模型来模拟简化的木材管胞结构,并赋予其脆性断裂相场模型,在不同加载速率下分析木材微观结构的断裂;Ostapska等[6]测量了挪威云杉木材I型劈裂试验中的裂纹演化,并依此设计一种算法获得裂纹尖端位置,根据裂纹路径数据推导了断裂能、临界应力强度因子和试验阻力曲线;Hartmann等[7]提出了一种基于RVE和fem的数值方法,模拟松材管胞在室内气候环境下的径向和切向压缩行为,并通过光学和激光-光学图像分析以及松材边材单板的拉伸和压缩试验进行验证;郭宇等[8]阐述了木材细胞壁微纤丝角、结晶度、纹孔和化学组分等对木材力学性能的影响规律,对未来细胞壁微观研究发展趋势进行了总结;蔡绍祥等[9]利用纳米压痕技术研究了马尾松木材不同高度、幼龄材、成熟材以及早材和晚材部位木材管胞细胞壁黏弹性变化;冯启明等[10]选取了杉木(Cunninghamia lanceolata)、白皮松(Pinus bungeana)和日本落叶松(Larix kaempferi)3种针叶树材,探究并比较位于不同生长轮的单根管胞的形态参数及拉伸力学性能。
综上,为进一步了解木材的力学性质、断裂过程,国内外学者深入研究了木材管胞的结构,并针对其微观结构进行建模仿真,亦有提出新的理论、方法模拟木材的裂纹扩展、断裂形式。针对管胞建模结构相关方向的研究,本研究提出一种木材螺旋管胞结构模型,选取挪威云杉(Picea abies)作为研究对象,利用Abaqus进行仿真,研究其横向切断过程,并对云杉试件进行实际切断试验,再将常规木材模型仿真结果及实际试验结果进行对比分析,并以此评价研究提出的螺旋管胞结构模型。
1 木材物理特性和参数
1.1 物理特性
木材作为一种天然的非均质复合材料,具有高度的各向异性性质,其机械性能与组织结构之间的关系非常复杂,力学性能也表现出强烈的非线性[11]。在木材切割过程中,超出木材弹性阶段的部分处于连续破坏力学和塑性的框架内,涉及到了正向弹性行为和塑性各向异性/各向异性硬化、各向同性的延展性破坏,还有切割过程中发生的巨大塑性变形,以及木材和刀具之间的接触和摩擦。
本研究建立了常规木材模型以及基于螺旋管胞结构的模型,使用ABAQUS/Explicit进行仿真解算。Explicit模块为显式计算,适合求解动力冲击、复杂接触、材料非线性和大变形的问题。
木材在受到外部作用力的情况下,首先表现出弹性的材料特性。建立木材弹性阶段本构方程,用以表达其弹性阶段的应力-应变关系,计算公式如下
σ=Dε。(1)
式中:σ为应力矩阵;ε为应变矩阵;D为刚度矩阵,由材料的工程常数决定。
对正交各向异性材料来说,若要表述其材料弹性,则需要9个独立常数。研究中,选取的木材在径向(R)、弦向(T)的物理性能大致相同,可視为横观各向同性材料,其刚度系数以及工程弹性常数可简化为5个,即EL(L方向弹性模量)、ER(R方向弹性模量)、νRT(RT面内的泊松比)、νLR(LR面内的泊松比)、GLR(LR面内的剪切模量),其中轴R轴T均为各向同性轴,轴L为对称轴。挪威云杉的弹性常数见表 1 [12]。
1.2 木材的参数
木材是一种具有代表性的非均质材料,这种材料的宏观性能跟其本身的微观结构联系紧密,而木材微观结构是极其复杂的,其复杂性主要包含了结构复杂性及组成成分的复杂性[13]。将所有因素都考虑进来是不现实的,在众多合理假设基础上对木材微观几何模型进行简化,将单个管胞细胞壁结构用多边形外壁和圆形内壁来表示。管胞在轴向(L向)相对于横截面(R-T面)来说无限长,只需分析R-T截面上管胞的排布情况。R-T截面上常见的管胞排布方式有正方形和正六边形排布,如图 1所示。
木材管胞细胞壁可分为初生壁、次生壁,而后者又可分为S1、S2、S3层,其中S2层是最主要的一层,占整个细胞壁厚的70%~90%。构成细胞壁的主要成分是微纤维,微纤维与纵向细胞主轴(即L轴)的夹角即为纤丝角,对木材的物理力学性质具有较大影响[14]。通常次生壁S2层的微纤丝与细胞轴的夹角为10°~30°,微纤丝角对木材细胞壁弹性模量、硬度、刚度和抗拉强度均有影响,且与这些细胞壁力学性能指标均呈负相关关系[15]。
受此启发,提出一种云杉螺旋管胞结构,如图2所示。该结构由6个管胞组成一个基本单元,R-T截面如图2(a)所示,呈正六边形排列;代表体积单元(RVE)示意图如图2(b)所示,各管胞均绕RVE单元中心轴线(即L向)进行一定角度螺旋,其中管胞螺旋角为α(单根管胞轴向与木材L向的夹角)。研究中螺旋方向取左旋,并取α=10°进行研究。
表1中的参数可描述木材的宏观力学性能,而简化后管胞的微观力学性能的参数,则需要在R-T截面内建立起两者之间的关系。对于六边形管胞排列形式,其中部分计算公式如公式(2)所示[16]。
ELρs=Elρ
ER=Emd3cosθw3(w2+sinθ)sin2θ
EL=Emd3(w2+sinθ)w3cos3θ
νRT=cos2θ(w2+sinθ)sinθ
νTR=(w2+sinθ)sinθcos2θ
GRT=Emd3(w2+sinθ)w7(2w2+1)cosθ。(2)
式中:E1为木材细胞壁1方向弹性模量,MPa;ρ为木材宏工密度,g/cm2;ρs为压缩木材密度,可认为是细胞壁密度, g/cm3;w为六边形管胞R-T截面边长, μm;d为管胞的细胞壁厚的2倍, μm;θ为管胞截面内角较小值减去90°,(°);Em为木材细胞壁在R-T截面上的杨氏模量,且有Em=El=Er, Er为木材细胞壁r方向弹性模量,MPa。
对于以上各式需要用到的参数具体数值,w=21 μm,d=7 μm,ρs=1.55 g/cm3,θ=30°[17]。由此最终得到的数据即为云杉微观弹性常数,见表 2。
根据以上公式计算得到云杉微观弹性常数并建立云杉的螺旋管胞结构模型后,需要用到Abaqus的MicroMechanics子程序将由此管胞构成的材料模型进行均质化处理。均质化方法即对非均质材料进行放大,在分析其结构后,取出某一个单胞作为代表性体积单元进行研究,再基于此建立力学模型,利用周期性条件均匀化条件以及一定的数学变换,最终可以得到与材料宏观等效的弹性模量和泊松比。MicroMechanics是一个Abaqus CAE用户子程序,具有友好用户界面,用于估算用户所创建的周期性RVE的均质有效弹性属性,并且所有计算都在Abaqus中完成,无须使用第三方软件。建立的云杉螺旋管胞结构RVE模型如图3(a)所示,作为对比,图3(b)为六边形排列的RVE模型,并且采用静态线框显示。
2 木材断裂仿真
2.1 试验选材
挪威云杉(Picea abies),又名欧洲云杉,原产于欧洲北部及中部。挪威云杉是一种轻质木材,干燥良好,易于加工,广泛用于生产细木工和结构构件。我国对挪威云杉亦有引种,生长较国内云杉快,具有较强的抗寒、抗病虫害能力,表现出较强的适应性[18-19]。
基于上述特性,选择挪威云杉作为木材切断试验的材料。
2.2 切断试验及仿真
本试验使用YD-100电子式木材切断力试验机,最大试验力为1 000 N,所配切断刀具开刃角度为20°,刃口截面为楔形。选用材料外形为长方体,横截面为边长10 mm的正方形,长度40 mm,如图 4所示,试验材料底部使用铸铁底座支撑于试验机,设置刀具下降行进速度为100 mm/min。
在Abaqus中建立刀具的模型,并将刀具设置为刚体,网格单元使用R3D4单元,这是一种四结点三维双线性刚性四边形单元。网格共划分为230个单元。
建立的云杉材料模型为长方体,横截面为边长10 mm的正方形,模型长度为40 mm。在Abaqus软件中为模型设置400个种子,共分为135 000个网格,网格单元使用C3D8R单元,这是一种八结点线性六面体单元。网格整体呈现为切断处较密集、远离切断处较稀疏的分布状态。建立的有限元模型如图 5所示,其中X、Y、Z分别对应木材的R、T、L方向。
设置模型的材料属性,将刀具和木材模型进行装配,在边界条件环节中,将云杉模型底面进行完全固定约束,将刀具设置为200 mm/min的速度垂直于云杉模型轴向(沿Y轴负方向)进行位移。在Abaqus设置好各步骤的参数后,提交作业任务进行仿真分析,如图 6所示,其中分析步时间增量设置为1×10-6 s。
2.3 结果与分析
使用云杉木材试件进行切断试验,获得切断过程中的切断力-时间曲线,并分别使用基于云杉宏观弹性常数建立的云杉模型、基于螺旋管胞结构并使用微观弹性常数RVE均质化处理建立的模型进行仿真,仿真完成后在Abaqus中进行后处理。
在进行云杉木材切断试验后,获取试验的切断力-位移数据并导出至Excel表格中;在2次仿真后,分别选取2次仿真中与刀具耦合的RF参考点,绘制切割力-时间曲线图,如图 7和图 8所示。
为方便对比分析,将切断试验输出的切断力-位移数据导出保存至Excel,并利用Origin绘图软件将实际试验与2次仿真获得的切断力-时间曲线绘制于同一个图上,将横坐标统一为刀具位移量,最终得到切断力-位移图,如图 9所示。
由图9可以看出,在刀具切断木材的过程中,切断力呈不断上升趋势,其中切断力所克服的除了尚未断裂的木材纤维对刀刃的阻力,还包括已切断部分对刀具侧面的摩擦阻力等。通过对比可看出,2次仿真获得的切断力曲线虽然不能完全贴合实际试验的曲线,但均能较好地靠近,而基于螺旋管胞结构模型仿真获得的曲线,相对于常规模型仿真曲线则更为接近。
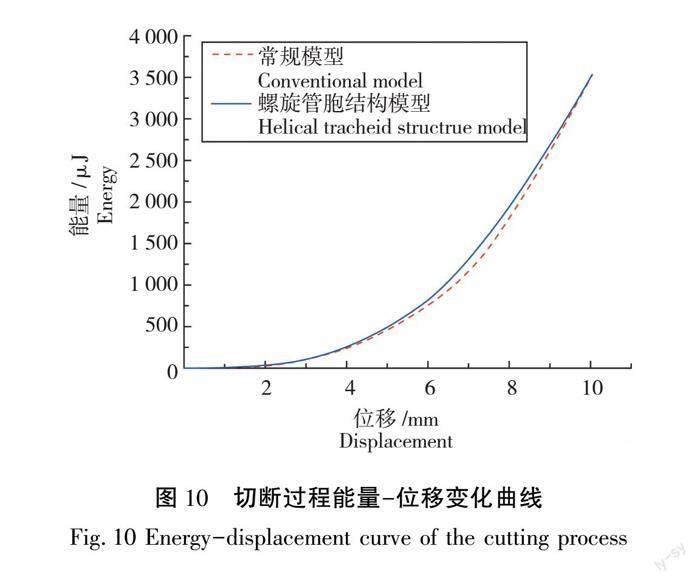
2次仿真中消耗能量的变化曲线如图 10所示,最终耗能基本相同。一般情况下,若要得出木材断裂过程中的总能量消耗,考虑到断裂力学理论,则可以通过木材断裂的能量释放率以及截面的面积得到。而在木材加工过程中,消耗能量的情况却远不及理想状态简单。传统的木材加工考虑加工过程中的总能量消耗,一般在于计算加工过程中的切削功率,即最大木材切割力与切割速度的乘积,再根据得出的结果来选择加工所需的机床电机型号。而分析实际加工过程情况以及图 9可知,木材加工过程中所需的切割力并非需要一直保持在最大值,若简单围绕最大功率来计算,势必会造成相当一部分的能量浪费。
在实际加工过程中,不同的加工手段也具有不同的特点。如在切削过程中,由于切削速度较大,除了木材断裂本身的能量消耗,还有刀具与木材摩擦所产生的巨大热量,以及所产生的木屑飞溅所具有的动能。而仅针对本研究而言,由于整个过程中并未产生飞屑,且刀具速度较慢,木材切断过程中的能量主要分为木材压缩变形所具有的应变能、在达到最大应力后断裂所消耗的断裂能以及小部分热能。由图 9可知本研究提出的云杉螺旋管胞结构模型在模拟加工过程中,对于切断力的部分较常规模型更为接近实际,在动态考虑切断力的情况下显然更具有参考性。
需要说明的是,實际的木材加工过程远比简单的有限元模拟要复杂得多。但通过分析切断过程中各部分的能量消耗以及切断力的变化,可为木材的加工过程提供一种能量消耗的计算思路,作为整个加工质量的评估条件之一。
3 结论
针对木材断裂问题的研究分析,提出一种木材螺旋管胞结构模型,采用挪威云杉作为试验对象,并利用Abaqus有限元分析软件对其进行切断仿真,获得了试件在一定刀具切断速度下的动态变化过程。对实际切断试验和有限元仿真的结果分析显示,基于本研究提出的木材螺旋管胞结构所建立的云杉模型能较好地模拟木材切断过程,并且在一定程度上优于使用常规方式建立的模型。本研究提出的螺旋管胞结构模型为木材断裂的研究提供了新方向,也对木材加工的工艺改进有一定的参考意义。
【参 考 文 献】
[1]杨忠.木材科学前沿研究与技术创新案例解析[J].国际木业,2020,50(6):80-82.
YANG Z. Case study of wood science frontier research and technology innovation[J]. International Wood Industry, 2020, 50(6): 80-82.
[2]KHELIFA M, KHENNANE A. Numerical analysis of the cutting forces in timber[J]. Journal of Engineering Mechanics, 2014, 140(3): 523-530.
[3]LUKACEVIC M, LEDERER W, FUSSL J. A. Microstructure-based multisurface failure criterion for the description of brittle and ductile failure mechanisms of clear-wood[J]. Engineering Fracture Mechanics, 2017, 176: 83-99.
[4]SALMEN L. Wood cell wall structure and organisation in relation to mechanics[M]//Plant biomechanics. Springer, Cham, 2018: 3-19.
[5]CARLSSON J, ISAKSSON P. Simulating fracture in a wood microstructure using a high-resolution dynamic phase field model[J]. Engineering Fracture Mechanics, 2020, 232: 107030.
[6]OSTAPSKA K, MALO K A. Wedge splitting test of wood for fracture parameters estimation of Norway Spruce[J]. Engineering Fracture Mechanics, 2020, 232: 107024.
[7]HARTMANN R, PUCH F. Numerical simulation of the deformation behavior of softwood tracheids for the calculation of the mechanical properties of wood–polymer composites[J]. Polymers, 2022, 14(13): 2574.
[8]郭宇,李超,李英洁,等.木材细胞壁与木材力学性能及水分特性之间关系研究进展[J].林产工业,2019,46(8):14-18.
GUO Y, LI C, LI Y J, et al. Research progress on the relationship between wood cell wall and wood mechanical properties and moisture properties[J]. China Forest Products Industry 2019, 46(8): 14-18.
[9]蔡绍祥,李延军,王思群,等.马尾松木材轴向管胞细胞壁黏弹性变异研究[J].林产工业,2021,58(11):1-7.
CAI S X, LI Y J, WANG S Q, et al. Study on the variation of viscoelasticity of cell wall of masson pine tracheid at axial direction [J]. China Forest Products Industry, 2021, 58(11):1-7.
[10]馮启明, 任素红, 吕建雄, 等. 三种针叶树材单根管胞形态与拉伸性能[J]. 木材科学与技术, 2022, 36(1):43-48, 74.
FENG Q M, REN S H, LYU J X, et al. Study on the morphology and tensile properties of single tracheids of three softwoods [J]. Chinese Journal of Wood Science and Technology, 2022, 36(1): 43-48, 74.
[11]孟祥鹏,关帅,王子奇.有限元方法在木质材料研究中的应用[J].科学技术创新,2017(9):1.
MENG X P, GUAN S, WANG Z Q. Application of finite element method in the study of wood materials[J]. Scientific and Technological Innovation, 2017(9):1.
[12]中国林业科学研究院木材工业研究所.中国主要树种的木材物理力学性质[M].北京:中国林业出版社,1982.
Institute of Wood Industry, China Academy of Forestry Science. Physical and mechanical properties of wood of major tree species in China[M]. Beijing: China Forestry Press, 1982.
[13]赵建博.云杉切削过程纤维断裂模拟及其钻削加工质量预测研究[D].哈尔滨:东北林业大学,2019.
ZHAO J B. The study of fiber fracture simulation of cutting process and drilling quality prediction of Spruce[D]. Harbin: Northeastern Forestry University, 2019.
[14]黄艳辉,赵荣军,费本华,等.木材微纤丝角的测定方法及其进展[J].西北林学院学报,2006(4):184-188.
HUANG Y H, ZHAO R J, FEI B H, et al. Measurement methods and development of wood microfibril angle[J]. Journal of Northwest Forestry University, 2006(4): 184-188.
[15]孙海燕,苏明垒,王玉荣.木材细胞壁力学性能与细胞壁组分和构造的相关性研究[J].林产工业,2018,45(10):22-27.
SUN H Y, SU M L, WANG Y R. Study on the relationship between the mechanical properties and the components, structures of wood cell walls[J]. China Forest Products Industry, 2018, 45(10): 22-27.
[16]GIBSON L J, ASHBY M F. Cellular solids: Structure and properties[M]. 2nd Edition. Cambridge: Cambridge University Press, 2014.
[17]SJOLUND J, KARAKOC A, FREUND J. Effect of cell geometry and material properties on woodrigidity[J]. International Journal of Solids & Structures, 2015, 62: 207-216.
[18]吳迪,孙岳胤,邢少博,等.挪威云杉扦插繁殖技术研究[J].防护林科技,2015(9):3.
WU D, SUN Y Y, XING S B, et al. Cutting propagation technology of Picea abies[J]. Protection Forest Science and Technology, 2015(9):3.
[19]王因花,梁燕,仲伟国,等.基质和生长调节剂对新墨西哥刺槐嫩枝扦插的影响[J].西部林业科学,2022,51(5):16-20,42.
WANG Y H, LIANG Y, ZHONG W G, et al. Effects of substrates and growth regulators on softwood cutting of Robinia neo-mexicana gray[J]. Journal of West China Forestry Science, 2022, 51(5): 16-20, 42.

