力学找形逻辑下的数字化设计和建造实践*

张海潮，余光鑫

1 形与力：结构力作为一种形式设计策略

根据结构受力设计高效且优美的建筑形式是一种行之有效的设计方法，力学找形旨在定义给定边界条件下结构的最佳几何形态。这种方法基于物理和美学进行设计，塑造了形式美，呼应了叔本华提出的重力荷载和建筑固有形态之间的“斗争”是建筑艺术审美的唯一题材[1]。自然界的重力促使结构选择反映其严谨秩序的科学形式，并严格约束设计过程，发展出空间、结构、形式统一的设计体系。

伽利略通过“找到合适的形状来赋予固体以使其在每一点都具有相同的抵抗力”选择效率和美观兼具的最优形式[2]，这种设计思维推动力学找形不断发展。自古以来，由公式定义的圆、抛物线等形状被用来在数学上确定砖石结构的形式和尺寸，由此发展出图解静力学、物理实验等确定结构形态的力学找形方法。进入数字化时代，计算性设计和数字建造技术提供了超越传统设计模式的创意设计过程，新的结构设计技术结合了数字工具与传统力学找形方法的优势。本文在总结既有力学找形方法的基础上，提出三种适合复杂结构形态生成的力学找形技术，通过阐释近年数字建造实践中实验性作品的设计策略和建构技术，探讨未来数字建筑设计中基于人机协作的力学找形模式。

2 形与力相融的设计方法和实践

建筑师通过图解、模型或数字技术结合理性结构思维与感性建筑审美，利用结构受力生成静力平衡的理想形式，创造符合结构逻辑的新颖空间形态。从应县木塔横直榫接的相叠构架[3]构成应对地震风压的活动榫构造（图1），到圣索菲亚大教堂圆顶过渡到方形支撑墩产生穹顶漂浮于中殿之上的微妙感受（图2），再到由不同高度风力确定埃菲尔铁塔的渐变折线形态（图3），建筑师对力学的敏锐感知使得这些由力约束的建筑形式展现出形与力相融的美感。

图1 应县木塔剖面图

图2 圣索菲亚大教堂剖面图

图3 莫里斯·科奇林“300m 高塔”设计草图

2.1 传统工程学时代的力学找形方法与实践

对建筑与结构关系的研究由来已久，基于图形或物理技术的图形静力学和模型实验被用于寻找适合结构力传递的三维形态（图4），这不仅是对数学定律的具象反映，也是对材料性能的真诚表达。

图4 传统工程学时代的力学找形研究发展脉络

在图形力平衡的研究领域，史蒂文(Simon Stevin)发表力的平行四边形图并展示绳索形成的索拱（funicular）形状，胡克(Robert Hooke)提出“正如悬挂柔软的线，被倒置为站立的刚性拱门”的反转定律[4]，瓦里尼翁（Pierre Varignon）则汇总了索拱多边形。库尔曼（Karl Culmann）基于平面平衡和力多边形的对偶性提出由表示几何形状的形式图(form diagram)和结构力的力图(force diagram) 组成的图解静力学[5]，基于力流构造形式逻辑的图解静力学通过分析存在于结构几何边界内的索拱曲线生成纯受拉或受压形式[6]。

许多建筑师通过实践促进了图解静力学的发展和创新。例如胡克与雷恩(Christopher Wren)使用图解静力学确认圣保罗大教堂的砖石圆顶是稳定的纯受压结构形式。高迪（Antoni Gaudí Cornet）设计桂尔公园市场大厅的柱顶梁为由上部受压拱形砖块和下部受拉抛物线形钢条构成的等强度梁形态以抵消弯矩[7]。古斯塔维诺（Rafael Guastavino Sr.＆Jr.）则使用压力平衡计算圣约翰大教堂球形圆顶结构的受力，在砌体内部产生推力线的地方放置瓷砖[8]。

钢筋混凝土薄壳能以很薄的结构厚度覆盖大跨度空间，在20 世纪初这类无弯矩且仅受切向应力的形式被广泛用于建筑设计[9]，空间结构通过变异和组合形成的复杂空间受力体系难以用力流图解分析判断受力合理性，成熟的计算工具和实验科学促使物理实验取代图解静力学成为重要的力学找形方法。高迪和奥托（Frei Otto）、伊斯勒（Heinz Isler）等运用悬挂模型作为找形工具，基于自然界物质自形成和自组织特性的物理实验是“在没有人为干预的情况下发生的”自然构造[10]，材料通过“模拟计算”实验自组织以找到给定边界设置的稳定形状。

结构建筑师通过物理找形寻求结构、形式与空间之间的平衡。例如高迪使用悬挂比例模型实验结果来确定科洛尼亚桂尔教堂地穴倾斜柱和拱顶的形式[11]。奥托运用不同特性的膜或网模型生成最小曲面、双曲面和负曲率边缘形式[12]，通过三种比例模型确定曼海姆多功能厅木网壳的整体形式、网格应力分布和结构竖立方式。伊斯勒则调整实验材料和切割模式来生成新型倒挂膜结构形式，通过倒转悬挂膜并放大到全尺寸建立BP 服务站和格洛特钦根室外剧院的屋顶索拱壳体。

2.2 数字化时代的力学找形方法与实践

模型实验能够有效确定简单结构原型的形态，却无法应对复杂形态和混合结构体系。性能驱动的运算化研究是数字化设计的新方向，结合数字模拟技术的力学找形通过多学科分析和优化，取代基于实验、经验的传统设计方法[13]。数字找形技术基于物理原理和输入算法—控制变量—输出形态的过程规则，使用计算机辅助设计技术在复杂图形设计界面中提供的数字工具生成复杂形式。结构信息的视觉表达和实时反馈使得结构被完全定义、建模和评估，综合结构选型、材料分析、表皮建构等多学科信息的数字构造模型强化了结构逻辑，由数字生成、模拟和优化促成方案涌现[14]。

亚历山大（Christopher Alexander）提出形式语法（Shape Grammar）将建筑设计划分为一系列子问题，通过定义找形规则来实现特定建筑形态。在计算机技术普及后，研究者利用参数化理论建立数字信息模型。其中粒子弹簧系统（Particle-spring, PS）是寻找纯受拉或受压结构形式的物理模拟算法，弹簧力和外力控制包含粒子、弹簧的初始拓扑网格系统振荡运动来模拟悬挂模型受力，迭代节点和弹簧的作用过程直到确定静态平衡结构[15]。在基于PS 的实时交互建模环境中使用迭代求解器确定粒子平衡位置，倒置重力作用下质量分布均匀的矩形悬挂网格平衡状态为拱壳形式[16]（图5）。布洛克（Philippe Block）基于射影几何、对偶理论和线性优化扩展图解静力学到三维的推力网络分析（Thrust Network Approach, TNA），控制定义边界内潜在索拱网络的自由度来生成重力荷载下的纯压拱形曲面[17]。在基于TNA的RhinoVAULT 插件中拉伸平行方向的力图以增加拱曲面局部区域受力，创建的高曲率瓷砖拱顶形式具有开放边缘和点支撑[18]（图6）。谢亿民、佐佐木睦朗（Mutsuro Sasaki）等基于有限元分析框架提出拓扑优化非线性形式的进化结构优化（Evolutionary Structural Optimization,ESO）、双向ESO（BESO）和三维扩展ESO（EESO）方法，从设计域中移除低效材料并添加到高应力区域以产生最佳刚度和体积的有机结构形式[19]。卡塔尔国家会议中心中类似树木交织的有机柱形式由EESO方法塑造，用于支撑外部屋顶挑檐（图7）。

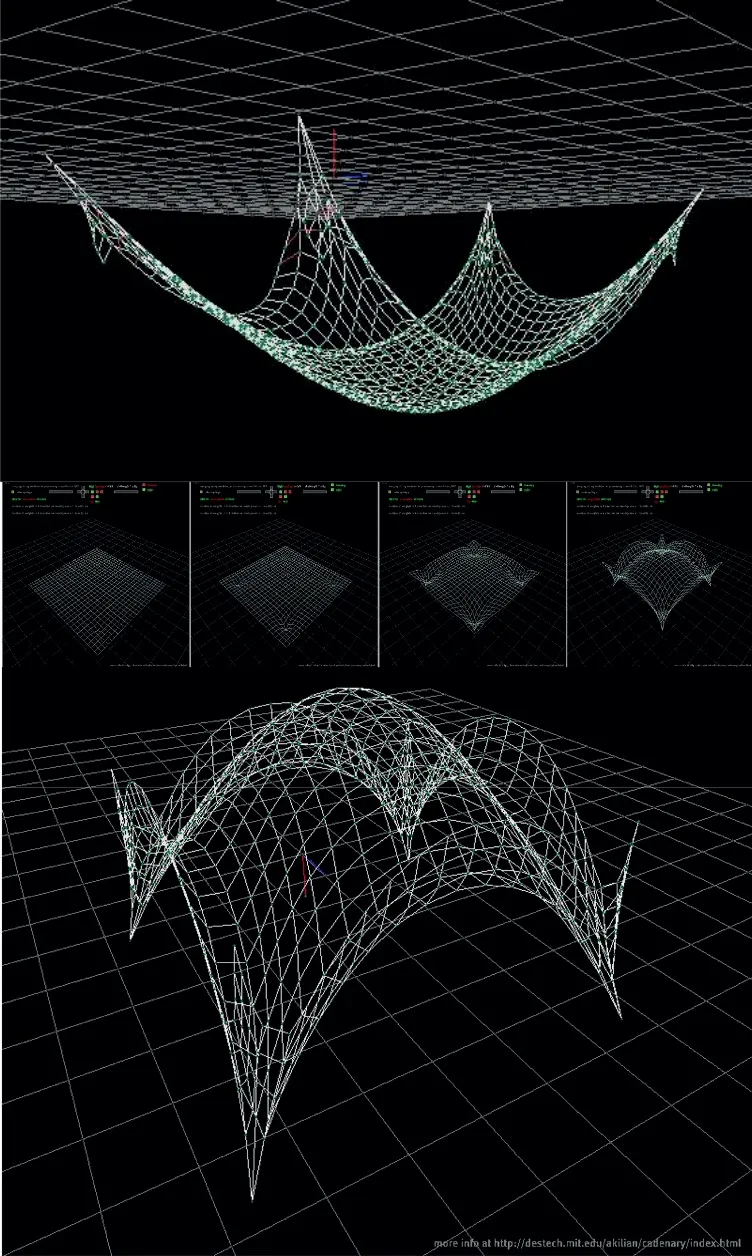
图5 上翘边缘网格壳的求解过程和平衡状态

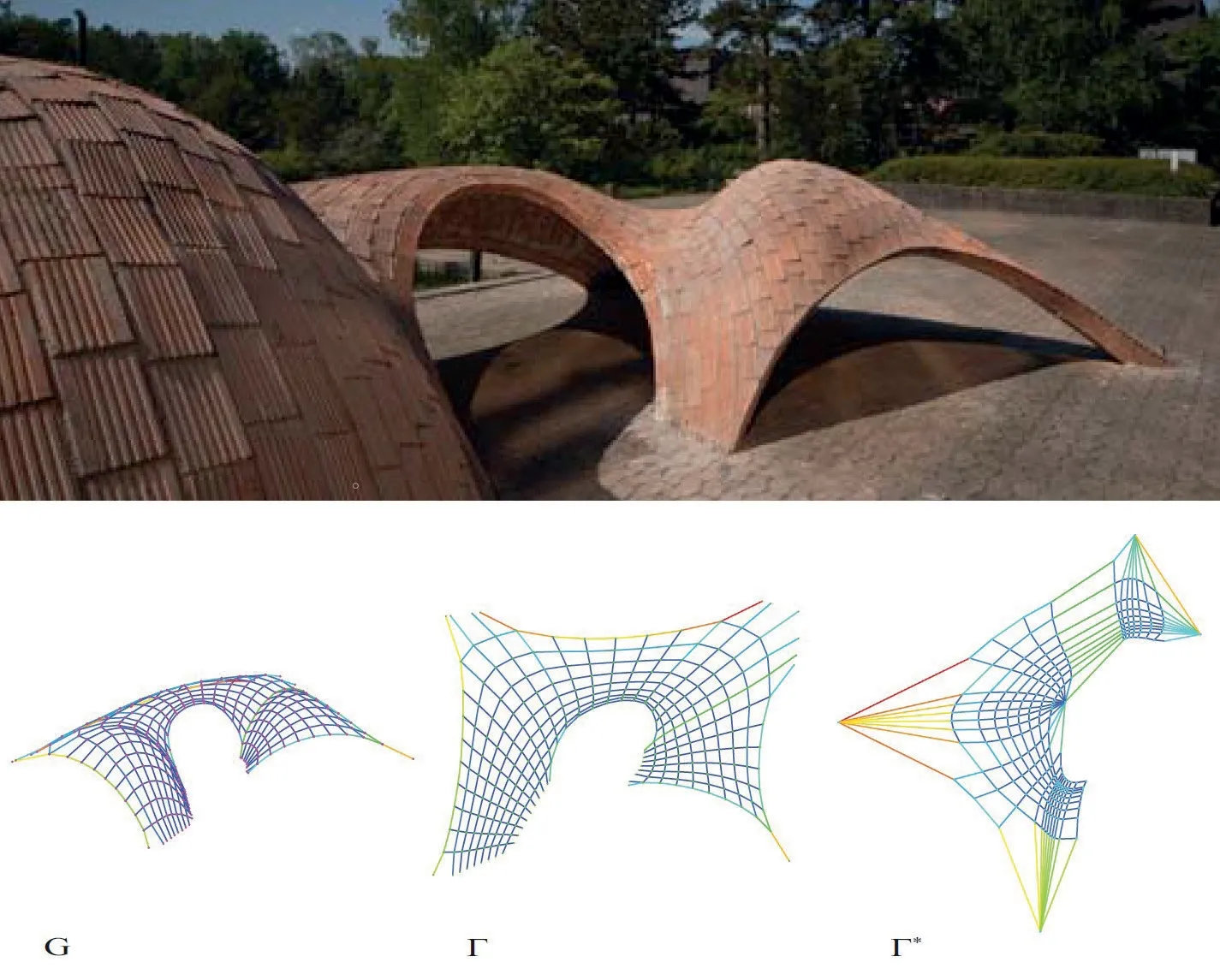
图6 Funicular Brick Shell 的结构和TNA 找形结果

图7 卡塔尔国家会议中心的有机树结构

最近不断增强的计算能力拓展了力学找形在三维空间的适用范围，为复杂空间结构的分析和设计提供新的技术路径（图8）。三维图解静力学领域发展出基于多面体（Polyhedron-based 3D Graphic Statics, PGS）和基于向量（Vector-based 3D Graphic Statics, VGS）的研究方法。其中阿克巴扎德（Masoud Akbazardeh）根据形式受力大小与其对偶力多面体面积对应原理提出PGS方法[20]，通过细分由封闭多面体组成的力图来改变索拱结构形式。该团队使用基于PGS 的PolyFrame 插件实现模块化玻璃桥的找形[21]，将定义拓扑结构和荷载分布的二维力图拉伸为力多面体再细分导出具有封闭多面体单元的双层形式图。VGS 方法则根据向量形式图和力图遵循的三维对偶性来实时控制杆件空间结构的形和力图解，支持向量式图解双向转换和处理为一系列参数定义[22]。基于VGS 和组合平衡建模的找形方法[23]通过可视化平衡结构的形和力图解以实时调整结构拓扑关系、内力和性能指标，生成受拉、受压和荷载工况组合下的新型空气支撑结构形式。针对PGS 的耗时找形过程，基于迭代机器学习算法的加速找形方法[24]通过构建和训练神经网络模型来加快结构性能评估和拓扑找形，代理模型评估输入力图细分规则与所选结构性能指标之间的非线性关系，预测满足结构性能和建造约束的理想形式并可视化整个解决方案空间。在拓扑优化领域，鲍鼎文等基于BESO 提出预测或干预拓扑优化过程的细节策略算法[25]，通过修改BESO 方法中元素过滤半径、局部体积分数或物理荷载和人工干预的协调权重等方面建立多半径BESO(MR-BESO)、多体积BESO(MV-BESO)和多权重BESO(MW-BESO)方法。该团队通过MWBESO 算法完成删除或添加模型材料的迭代步骤，确定C形壳体的最佳结构形态[26]。在特定结构找形领域，曹婷提出新型光滑复合双曲面结构的分析方法[27]，由双曲抛物面基本单元光滑拼接形成的自由曲面壳体在力学上遵循结构传力的共面原则以避免产生弯矩。光滑复合双曲面结构的找形算法通过实时数据优化壳体形态，生成符合控制参数的双曲面结构壳体[28]。黄蔚欣等提出弯曲主动编织结构的网格生成和结构模拟算法来确定由均匀弹性杆组成的自由曲面网格壳形态[29]，Kagome 网格形式通过曲率控制原理和弯曲主动机制连续传递应力。这种由网格重建-细分生成和结构模拟优化算法构成的数字系统被用于生成多向编织网壳结构的立体雪花造型[30]。

图8 力学找形领域代表性的前沿研究和实践

采用力学找形方法设计的数字建造作品不断涌现。例如“云市”展亭[31]通过使用节点位移优化方法调整法线方向的结构节点位置以应对曲面出挑形变，凹凸网格形态增强整体刚度（图9）。“蝶变”构筑物[32]通过结构应力云图和力流方向确定海帕壳体的“蝴蝶”纹理，基于泰森多边形算法生成“蝴蝶”打印形状（图10）。“复合纤维桥”[33]通过Ameba 插件结合最优体积百分比系数生成桥体形态，根据受力方向排布编织纤维并直线化拟合结构主应力迹线确定打印形式（图11）。

图9 “云市”展亭

图10 “蝶变”构筑物

图11 “复合纤维桥”

3 基于力学找形的数字建造实践

计算机辅助设计和制造技术的发展实现从设计到制造的信息无缝传输，从计算机屏幕到数控机器的“文件到工厂”连续过程，结构参与到早期设计生成阶段，建筑与结构的关系从“后验型”转变为“先验型”，二者基于共享计算工具合作进行结构创新[34]。数字建造处于当代工程学前沿，已经发展成融合结构设计和建筑概念的新媒介。随着数字设计转向物理建造，虚拟的自由形式将转换为合理且可建造的形式，建造方法使用与找形方法相似的规则，使得建造性能标准和材料特性与数字模拟时相符。在应用力学找形方法的数字建造实践中，团队基于数字设计工具和数字建造工艺进行力学找形，将结构合理性推导与设计过程相结合。

3.1“钢铁之心”（Iron Heart）

2016 年，作为“机器人金属弯折”数字建造工艺的应用实验，“钢铁之心”项目在主题为“图解思维与数字建造”的第六届“上海数字未来”工作营中建造完成，团队借助力学找形数字技术设计并搭建出一个钢铁装置。

刚性结构的形态会导致结构内部产生扭矩和形变，从而影响结构稳定性。基于最大机械效率和最少材料使用的结构承载力较强，其形式具有最小的弯矩、应变能量和形变，使得结构表面的能量最小化[35]。应力迹线的疏密和走向被用来表示结构应力大小和力流路径，越短的力流路径意味着结构具有更大刚性和更小形变，因此应力迹线可作为形式优化的媒介。基于进化和自组织原则的数字算法通过拓扑的交互式分析来评估形式，迭代计算应力和形变对形式的影响，生成符合拓扑关系的最佳结构形式。Rhino—Grasshopper 平台的Millipede 插件通过预设结构重力荷载和形变，可视化结构内部应力迹线，根据应力线分布调整刚性装置的几何形态或材料分布，对比不同优化组合的结构形变性能数据去选择最合理的三维形式，以此建立半可控、半自动化的找形策略。

在“钢铁之心”的力学找形过程中，我们选择形式语法生成的最佳空间路径作为设计原型，由钢板组成基础几何形态作为找形的支点，初步建立应力、扭矩、形变、材料之间的关联并开始力学找形（图12）。给定基本体量，在Millipede 中对装置模型悬挑的最大扭矩处施加荷载来模拟极限应力条件，基于推算的力流分布生成结构产生潜在形变时的空间连续应力线（图13a），将其抽象为结构加强线条再轧制为钢板面的图案形态（图13b），图案加强钢板面的受力性能以确保在应力传递过程中装置不发生垂直于应力线的形变，从而强化结构稳定性。借助反映钢板各处受力状态的应力线生成的预应力钢板形式呈现出自组织特征，在完善刚性结构力学性能的过程中实现形式优化。

图12 基于力学找形的“钢铁之心”设计过程

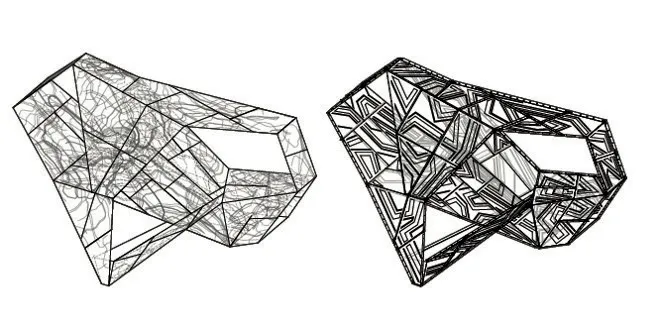
图13a 极限条件下的结构应力线

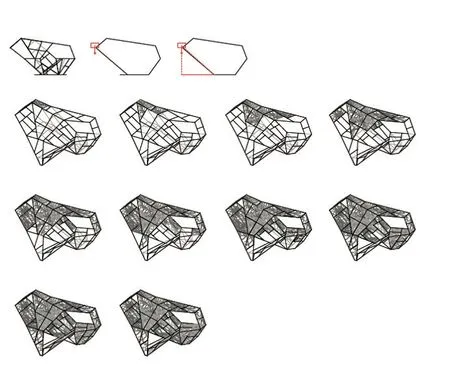
图13b 面板图案形式

在“钢铁之心”的建造过程中，使用算法和数字机器人技术探索适用于钢材的数字建造方法。首先基于遗传算法所提供的搜索技术，选择材料使用最少的曲面分区方式（图14a），将所有曲面划分为若干面板组件，得到满足材料强度、挠度和经济用钢量的分区方案。进而通过面板分析对比57 块面板与标准钢板的面积（图14b），确保数字机器人能够冷轧并切割出小于标准钢板的组件。最后，按照软件模拟的建造步骤用螺栓将钢板连接组成最终形态（图15），即完成“钢铁之心”装置的搭建。

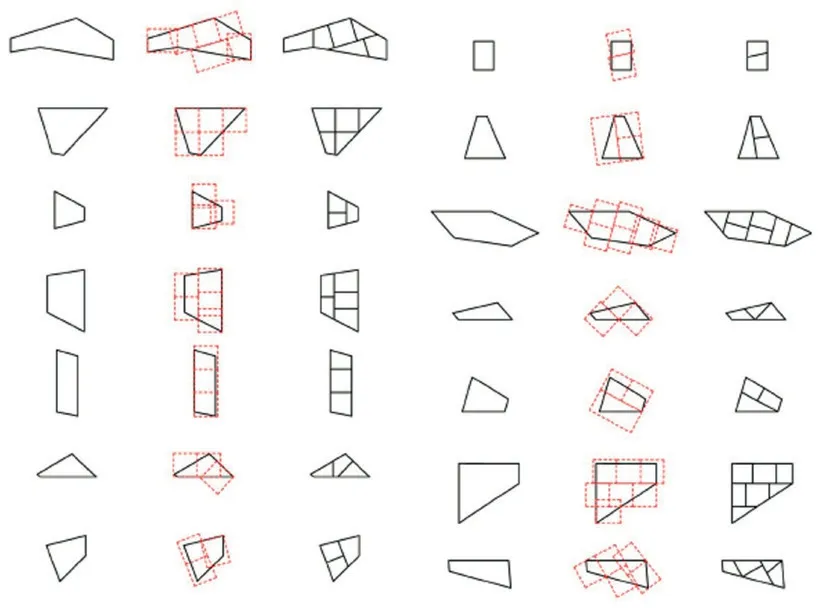
图14a 曲面划分方案

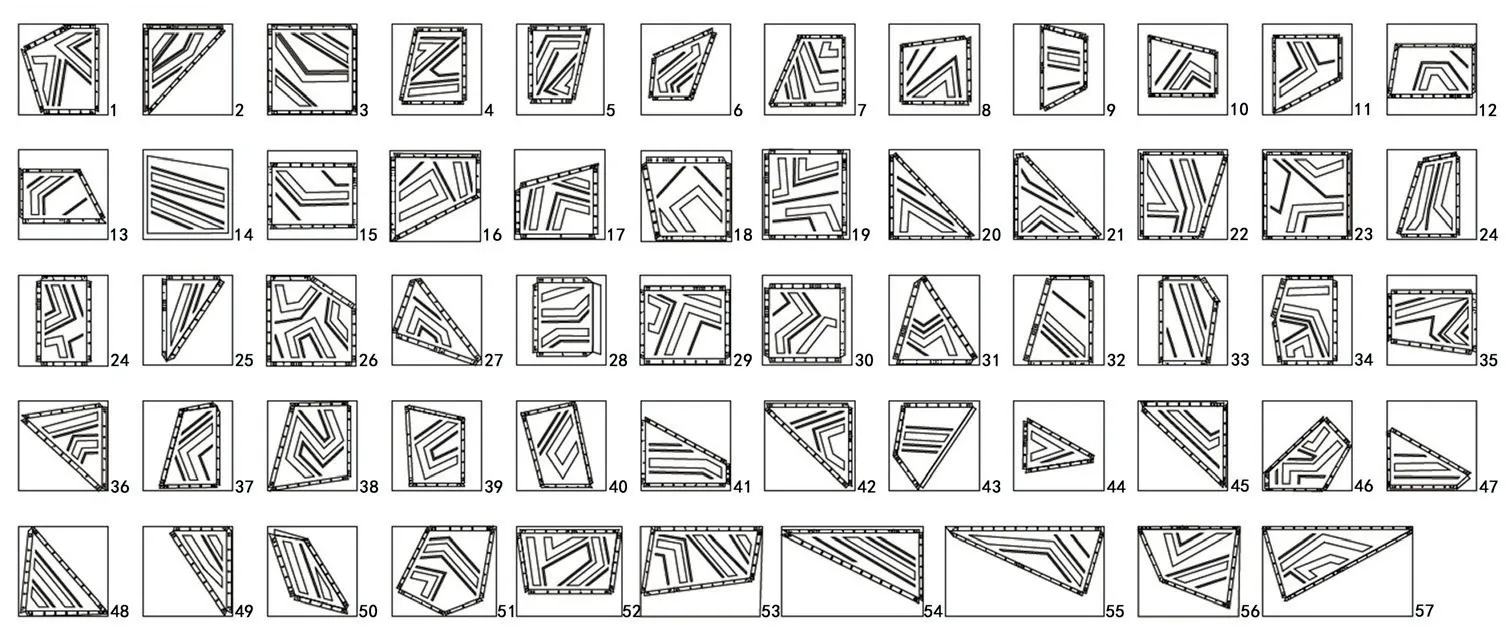
图14b 面板面积分析

图15 “钢铁之心”实景

3.2 “索拱漏斗壳”（Funicular Shell）

在2017 年的“应用数字技术的模块化微建筑建造研究”项目中，团队通过力学找形探索索拱壳体的形式、结构一体化设计，基于数字图解静力学和数字机器人技术实现了复杂薄壳空间结构的设计和建造。

结构和形式相关联的索拱壳结构因其无弯矩而纯受压的推力曲面类似于相互连接的悬链线网格，成为以最少材料建立最大刚度结构的最佳形式选择。三维图解静力学使用数字空间模型设置形式图和力图，提供无需投影的三维计算方法研究形与力关系，可视化力流构建形式的过程[36]。TNA 是使用离散网络分析和优化复杂索拱曲面的图形静力学方法，其中形图解定义结构平面形状和受力模式，力图解显示壳体水平推力的分布，根据二维图解求得与垂直荷载平衡的索拱推力网络，代表壳体内部压力与荷载平衡时的空间形状。该过程使用代表推力网络水平投影达到平衡状态的形图解和对应比例的力图解，找到力图解中每组边界顶点与给定垂直荷载平衡时的推力网络并转化为纯受压壳形态[37]。Rhino—Grasshopper 平台的交互式数字插件RhinoVAULT 基于TNA 原理可视化控制形和力图解的双向交互过程，生成索拱壳体形式。

在“索拱漏斗壳”的力学找形过程中（图16），在RhinoVAULT 中输入平面边界条件并生成控制网络，将薄壳水平投影的平面拓扑网络作为找形原型，确定结构支点位置后不断迭代增加竖向荷载下曲面的曲率，得到水平和竖直方向上均达到受力平衡状态的纯受压网络（图17a），从而生成最符合目标曲面的索拱薄壳形式。接着将推力网络转化为对应的NURBS 曲面，通过薄壳曲面上的点模拟该处的力流方向和轨迹。曲面等高线与力流轨迹的相交点作为同时符合力流与等高线错位分布要求的离散点，通过位置优化使其领域值均匀，使用以优化点为中心的正六边形对内、外表面进行曲面空间分割以获得薄壳组件（图17b），从而避免产生结构通缝，消除模块之间相对滑动，确保组成薄壳形式的面板内部无弯矩且只传递轴向压力。因索拱曲面主要被漏斗状的中心落地点支撑，可形成一个具有开放拱形边缘的非线性屋面。

图16 基于力学找形的“索拱漏斗壳”设计过程

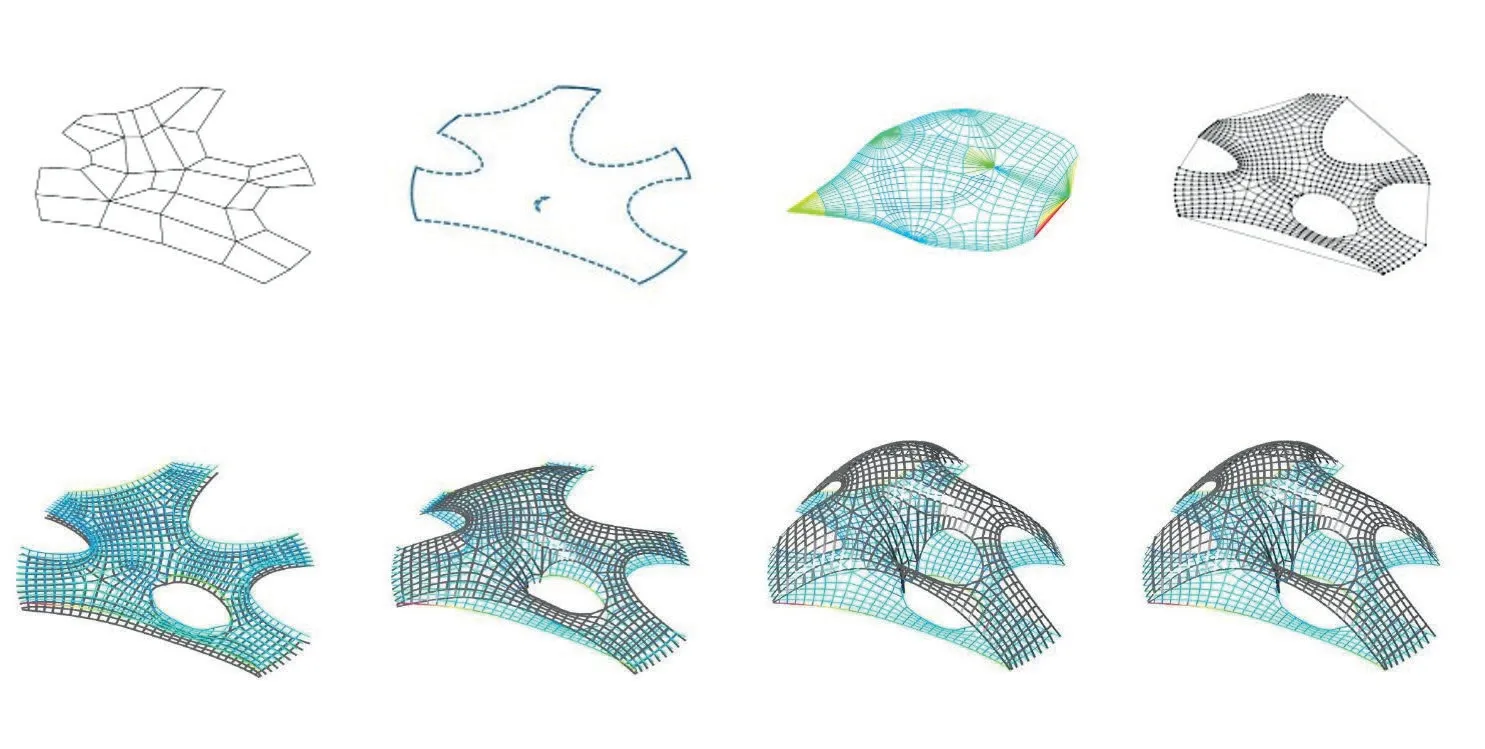
图17a TNA 迭代找形过程

图17b 曲面分割过程

在“索拱漏斗壳”的建造过程中，通过遗传算法和数字机器人技术实现轻型薄壳的数字化建造。首先使用遗传算法创建各种可能的组件雕刻方案（图18a），迭代计算出包裹所有曲面组件的最小体积立方体，将其作为雕刻组件的标准板材。然后通过软件仿真模拟整个雕刻过程，指导单台数字机器人在16d 内以每件2h 的平均速度完成200 块组件的雕刻工作（图18b）。最后现场施工耗时8h 完成“索拱漏斗壳”构筑物的搭建（图19）。

图18a 遗传算法确定雕刻方案

图18b 机械臂雕刻过程

图19 “索拱漏斗壳”实景

3.3 “趣村竹园——若浮廊”（Tensioned Bamboo Gallery Bridge）

在以“乡村之趣”为题的“趣村夏木塘——2018 第三届国际高校建造大赛”中，团队通过数字设计工具实现张拉整体结构的力学找形和在地建造，以一座轻盈漂浮的“若浮廊”竹桥激活村入口水塘空间的活力。

基于竹材顺纹理方向抗压强度大的结构性能，并根据竹材与现代结构相结合的策略，选择比空间框架或桁架系统更轻、更坚固和更具成本效益的张拉整体结构设计竹桥形式，利于发挥原竹轴向受压材性并展示张拉结构的轻巧力学张力。张拉整体（Tensegrity）系统基于富勒（R.Buckminster Fuller）测地线圆顶中三角形网格杆的轴向受力规律，是一种空间、网状和轻质结构系统，由一组在空间中连接的连续受拉组件和一组在空间中独立的不连续受压组件组成[38]。与重力荷载下连续受压的传统结构不同的是，张拉整体结构通过孤立受压构件和相连受拉构件的连续路径实现连续张力概念，可利用低自重材料、小尺度构件建造大跨度结构。该结构找形的关键是确定其平衡配置，通过施加不同类型约束生成不同形式，调整约束分组或比率生成替代形式[39]。Rhino—Grasshopper 平台的Kangaroo 插件是基于动态松弛技术开发的物理模拟引擎，与虚拟物理力进行交互来实时分析和反馈形式、受力条件的变化，以视觉方式模拟材料力学特性[40]，确定张拉整体形式。

在“若浮廊”的力学找形过程中（图20）建立张拉竹构件的找形方法，通过Kangaroo 模拟所有竹制维护组件的物理张拉形态，生成单一张拉整体系统难以实现的复杂形式。首先输入未张拉时各维护组件中竹竿和钢索的初始状态，确定结构中控制张拉的互连节点，施加荷载并根据不平衡力和牛顿定律对节点进行轴向受力分析以跟踪其运动方向。以节点位置为优化参数，将节点往受力方向移动并更新结构形状，检验张拉结构是否达到静态平衡的稳态，最终确定节点受力平衡时的张拉形式（图21）。结构网络中分配加权质量和刚度的节点通过模拟几何和刚度参数变化实现大量位移，使得预定义拓扑结构随时间运动到平衡状态的最小表面形状，生成结构和形式一体化的最佳形式。

图20 基于力学找形的“若浮廊”设计过程

图21 顶面、侧面维护组件的张拉整体形态和竹桥形式

在“若浮廊”的建造过程中，针对受力、节点、预制装配等问题探索相应建造方法。新型节点设计改变竹构件的固有连接方式，使用树脂密封极易被潮湿环境腐蚀的原竹端头断面，再通过固定于凝固树脂中的金属杆件拉接钢索（图22）。根据竹竿纯受压而钢索纯受拉的结构特性优化材料尺寸，采取预制标准化竹构件和钢索的方式，现场张拉竹制组件成形并安装到钢结构桥体，完成竹桥的装配搭建。然后应用相同的结构逻辑设计灯具、家具，形成灵活移动的小尺度张拉整体结构模块。最后交错搭配芦苇丰富桥面光影变化，辅以灯光和水雾增添朦胧趣味，使水塘区域成为标志性公共空间（图23）。

图22 竹构件节点的制作过程

结语

形态生成应能体现建构逻辑，力学找形通过结构、材料和形式之间的关联，成为整合建筑和环境的协同设计方法。结合计算性设计的数字化力学找形作为形式生成和优化方法，提供理解几何逻辑和模拟物理的新图形交互模式，通过实时交换结构、形式、表皮数据，实现高性能结构和经济性建造。本文以数字建造为切入点建立数字技术驱动下整合设计策略和建造方法的力学找形模式，以应用不同找形方法的数字建造项目为例展示力学找形逻辑指导的数字设计和建造过程。正如胡克反转定律中的形式原型，形和力的结合将引导建筑师理解受力生成形式的过程，形成类似“对表象背后秩序的感觉”[41]的设计直觉，探索解决设计问题的无限形式可能性。

图片来源

图1：https://m.thepaper.cn/newsDetail_forward_14226434

图2：https://www.pallasweb.com/deesis/hagia-sophiabuilding-plans.html.

图3：https://www.toureiffel.paris/en/news/history-andculture/maurice-koechlin-engineer-without-whom-tower-wouldnot-exist.

图4：作者基于参考文献[4-12]的信息整理绘制；

图5：参考文献[16]；

图6：参考文献[37]；

图7：参考文献[19]；

图8：作者基于参考文献[20-30]的信息整理绘制；

图9：参考文献[31]；

图10：参考文献[32]；

图11：参考文献[33]；

图12-23：作者绘制或拍摄。